1 Introduction

The famous “ham sandwich” theorem of Stone, Tukey, and Steinhaus [13, 14] asserts that every d absolutely continuous probability measures in ℝd can be simultaneously partitioned into equal parts by a single hyperplane.

In [3] Bereg and Kano raise the following question (in the planar case): If we are given d+1 measures in ℝd and want to cut the same (but unknown) fraction of every measure by a hyperplane, then what assumptions on the measures allow us to do so? Certainly, additional assumptions are required because if the measures are concentrated near vertices of a d-simplex then such a fraction cut is impossible. A sufficient assumption is described below.

Definition 1

Let μ 0,μ 1,…,μ d be absolutely continuous probability measures on ℝd and let ε∈(0,1/2). Call the set of measures ε-not-permuted if for any halfspace H the inequalities μ i (H)<ε for all i=0,1,…,d imply

$$\mu_i(H)\ge\mu_j(H), \quad \text{for some } i<j. $$

Remark 1

For ε>0 consider all halfspaces H in ℝd such that μ i (H)<ε for all i and the values μ i (H) are pairwise distinct. If we arrange the values μ i (H) in the ascending order, then we get some permutation of {0,1,…,d}. So there is an order of μ i such that the measures μ i are ε-not-permuted if and only if in such a way we cannot get all possible permutations of the d+1 element set. In the sequel, for example in Theorem 1, we are actually interested in measures that are ε-not-permuted for at least one order of them.

Remark 2

A natural example of ε-not-permuted measures appears when the support of one measure lies in the interior of the convex hull of the union of supports of the other d measures. In this case the measures are ε-not-permuted for sufficiently small ε.

Now we state the main result.

Theorem 1

Suppose μ 0,μ 1,…,μ d are absolutely continuous probability ε-not-permuted measures in ℝd for some ε∈(0,1/2). Then there exists a halfspace H such that

$$\mu_0(H) = \mu_1(H) = \cdots= \mu_d(H) \in[ \varepsilon, 1/2]. $$

Note that in [2, 6, 8] a similar problem was considered: Cut by a hyperplane a prescribed fraction of each of d measures in ℝd. Again, this cannot be done in general and some additional assumptions are needed.

A straightforward consequence of Theorem 1 follows by considering one measure concentrated near a point.

Corollary 1

Suppose μ 1,…,μ d are absolutely continuous probability measures in ℝd and p is a point in the convex hull of their supports. Then there exists a halfspace H such that

$$\mu_1(H) = \mu_2(H) = \cdots= \mu_d(H) $$

and p∈∂H.

In Sect. 4 we consider a discrete version of Theorem 1, replacing measures by finite point sets. This is in accordance with the initial statement of the problem in [3].

Finally, in Sect. 5 we consider a problem of cutting the same prescribed fraction of every measure, this time allowing cutting with a convex subset of ℝd.

2 Ham Sandwich Theorem for Signed Measures

In order to prove Theorem 1 we need a version of the “ham sandwich” theorem [13, 14] for signed measures.

Definition 2

A difference ρ=μ′−μ″ of two absolutely continuous finite measures on ℝd is called a signed measure. In other words, a signed measure is represented by its density from L 1(ℝd).

Theorem 2

(Ham sandwich for signed measures)

Suppose we are given d signed measures ρ 1,…,ρ d in ℝd, then there exists a (possibly degenerate) halfspace H such that for any i,

$$\rho_i(H) = 1/2 \rho_i\bigl(\mathbb{R}^d \bigr). $$

Remark 3

A degenerate halfspace is either ∅ or the whole ℝd. We cannot exclude degenerate halfspaces in this theorem when ρ i (ℝd)’s are all zero. The reason is the same for which we cannot exclude the “ε-not-permuted” assumption from Theorem 1, see also Remark 4 below.

Proof

The classical proof from the book of Matoušek [11] passes for signed measures (the authors learned this fact long ago from Vladimir Dol’nikov). Identify ℝd with ℝd×{1}⊂ℝd+1. Parameterize halfspaces \(\tilde{H}\subset\mathbb{R}^{d+1}\) with boundary passing through the origin by their inner normals. So all halfspaces \(H = \tilde{H}\cap\mathbb{R}^{d}\times\{1\}\) (including degenerate) are parameterized by the unit sphere S d.

If we map every halfspace to the vector

$$\bigl(\rho_1(H) - \rho_1\bigl(\mathbb{R}^d \setminus H\bigr), \dots, \rho_d(H) - \rho_d\bigl(\mathbb{R}^d\setminus H\bigr)\bigr), $$

then we obtain a continuous odd map P:S d→ℝd; by the Borsuk–Ulam theorem [5] (see also [11]) one halfspace must be mapped to zero. □

3 Proof of Theorem 1

As the first attempt we try to apply the ham sandwich theorem for signed measures to

$$\rho_1 = \mu_1 - \mu_0, \rho_2 = \mu_2 - \mu_1, \dots, \rho_d = \mu_d - \mu_{d-1}. $$

This way we easily obtain a halfspace H such that μ 0(H)=μ 1(H)=⋯=μ d (H). But the halfspace H may be degenerate or μ i (H) may be all zero. This is not what we want.

Remark 4

By the way, we see that starting from three measures μ i on ℝ2 distributed along three rays emanating from vertices of a regular triangle T and going in the direction opposite to the center of T, we cannot cut the same fraction (possibly zero) of these measures with a non-degenerate halfplane. The same example generalizes to higher dimensions and shows that in the ham sandwich theorem for signed measures we cannot avoid using degenerate halfspaces when all measures satisfy ρ i (ℝd)=0.

So let us perturb the signed measures with a small positive parameter s:

$$\rho^s_i = (1+s)\mu_i - \mu_{i-1},\quad \text{for }i=1, \dots, d. $$

Now Theorem 2 gives a halfspace H with:

$$ \rho^s_1(H) = \cdots= \rho^s_d(H)=s/2. $$
(1)

This is equivalent to the following equalities:

$$ \mu_{i-1}(H) = (1+s)\mu_i(H) - s/2 = \mu_i(H) + s \bigl(\mu_i(H) - 1/2\bigr). $$
(2)

Suppose μ i (H)<ε for all i=0,…,d. Then we have μ i (H)<1/2 and s(μ i (H)−1/2)<0. Hence,

$$ \mu_{i-1}(H)<\mu_i(H),\quad \text{for}\ i=1, \dots, d. $$
(3)

This contradicts the assumption that the measures are ε-not-permuted.

Hence the inequality μ i (H)≥ε for some i is guaranteed while we decrease s to 0, and in turn it guarantees (remember that we can interchange H and ℝd∖H!) that H cannot approach degenerate halfspaces ∅ and ℝd. So we assume by compactness that H tends to a certain halfspace as s→0 and going to the limit in (2) together with (1) we obtain the conclusion.

4 Discrete Version

In the paper [3] Bereg and Kano consider a discrete version of this theorem in the plane. They call a line ℓ balanced if each halfplane bounded by ℓ contains precisely the same number of points of each color.

Theorem 3

(S. Bereg and M. Kano [3])

Let S be a set of 3n≥6 points in the plane in general position colored in red/blue/green such that

  1. (i)

    the number of points of each color is n;

  2. (ii)

    the vertices of the convex hull of S have the same color.

Then there exists a balanced line of S.

Here we generalize the result of Bereg and Kano. For every directed line ℓ we write x≤ ℓ y if the projection of x to ℓ has not greater coordinate than the projection of y to ℓ.

Theorem 4

Let S be a set of (d+1)n points in ℝd in general position partitioned into colors S=S 0∪S 1∪⋯∪S d so that:

  1. (i)

    the number of points of each S i is n;

  2. (ii)

    for any directed line ℓ there exist two colors i and j, i<j, and a point x∈S i such that for any y∈S j we have y≤ ℓ x.

Then there exists a balanced hyperplane h, or in other words, a hyperplane such that each halfspace bounded by h contains precisely the same number of points of each color.

Proof

The proof follows almost directly from the continuous version. Replace each point by a solid ball centered in it and of radius r>0 sufficiently small so that there is no hyperplane that intersects any d+1 balls at the same time and for any partition of points of S by a hyperplane there exists a hyperplane that separates the corresponding balls accordingly. Since the points are in general position, such r does exist.

Balls of each color generate absolutely continuous measures. So we have d+1 absolutely continuous measures; multiplying them by the same constant we make these measures normalized; denote them by μ 0,μ 1,…,μ d .

Now, as in the proof of Theorem 1, we consider signed measures \(\rho^{s}_{i} = (1+s)\mu_{i} - \mu_{i-1}\) and find a halfspace H such that \(\rho^{s}_{1}(H) = \cdots= \rho^{s}_{d}(H)=s/2\).

We show that μ i (H) cannot be less than 1/n for all i. Suppose it is so. Then again using (2) we get:

$$ \mu_{i-1}(H)<\mu_i(H),\quad \text{for }i=1, \dots, d. $$
(4)

Consider a line ℓ inner-normal to H and colors i and j from condition (ii) for this line. Suppose μ i (H)<μ j (H)<1/n. The hyperplane ∂H intersects at least two balls of color j, otherwise the inequality would be μ i (H)≥μ j (H) by condition (ii). Under the above assumptions, every hyperplane can pass through at most d balls. Therefore there exist two colors k and m that do not intersect with ∂H and therefore with H (in the opposite case μ k (H) or μ m (H) would be at least 1/n). Hence we have μ k (H)=μ m (H)=0 in contradiction with (4). So for at least one i the measure μ i (H) is at least 1/n.

As s goes to 0, the halfspace H tends to a certain halfspace H 0. Its border hyperplane h=∂H cuts an equal positive fraction of every measure μ i .

If h touches no ball where the measures are concentrated, then we are done. But a problem can occur if h intersects some balls. Since the points in S are in general position, the hyperplane h touches at most d of them (denote the corresponding subset of X by I) and we can perturb h so that an arbitrary subset J⊆I will be on one side of h while I∖J will be on the other side of h. Thus we may “round” the fractions of the measure in any way we want and equalize the numbers of points in H for all the colors (compare with the proof of Corollary 3.1.3 in [11]). □

Remark 5

As in Remark 1 we can describe point sets satisfying condition (ii) in terms of permutations: For any directed line ℓ the order of points with least (among the points of the same color) projection to ℓ gives a permutation of colors {0,1,…,d}; a colored point set satisfies condition (ii) for some order of colors if and only if we cannot get all permutations this way.

Let us give a simpler but still useful assumption on S:

Corollary 2

Let S be a set of (d+1)n points in ℝd in general position colored in colors 0,1,…,d so that:

  1. (i)

    the number of points of each color is n;

  2. (ii)

    points of one color lie in the convex hull of the union of points of the other d colors.

Then there exists a balanced hyperplane h.

5 Cutting a Prescribed Fraction by a Convex Set

Let us state another problem about cutting the same fraction of several measures:

Problem 1

The dimension d and the number of measures k>1 are given. For which α∈(0,1) for any absolutely continuous probability measures μ 1,…,μ k on ℝd it is always possible to find a convex subset C⊂ℝd such that

$$\mu_1(C) = \cdots= \mu_k(C)=\alpha? $$

For α=1/2 and k=d a positive solution to this problem follows from the ham sandwich theorem. If α>1/2 then considering two measures, one concentrated near the origin and the other concentrated uniformly near a unit sphere, we see that there is no solution.

If k>d+1, one can consider d+2 measures concentrated near the vertices of a simplex S and the mass center w of S; in this case, any such C must contain a neighborhood of w and therefore cannot cut α of the corresponding measure.

In [15] Stromquist and Woodall solved a similar problem for k measures on a circle and cutting it by a union of k arcs.

Using the results on measure equipartitions from [1, 9, 12] we are able to solve Problem 1 for d+1 measures:

Theorem 5

Suppose μ 0,μ 1,…,μ d are absolutely continuous probability measures on ℝd and α∈(0,1). It is always possible to find a convex subset C⊂ℝd such that

$$\mu_0(C)=\mu_1(C) = \cdots= \mu_d(C)=\alpha, $$

if and only if α=1/m for a positive integer m.

Proof

First, we prove that it is possible if α=1/m. Following [12] it is sufficient to consider the case when m is a prime and use induction. Consider the space of functions

$$L = \Biggl\{a_0 + \sum_{i=1}^d a_ix_i + b \sum_{i=1}^d x_i^2 \Biggr\}. $$

This space has dimension d+2. Recall that a generalized Voronoi partition corresponding to an m-tuple of pairwise distinct functions {f 1,…,f m }⊂L is defined by

$$C_i = \bigl\{x\in\mathbb{R}^d : f_i(x) \le f_j(x)\ \text{for all}\ j\neq i\bigr\}. $$

In this case, [9, Theorem 1.3] asserts that there exists a generalized Voronoi partition corresponding to a subset {f 1,…,f m }⊂L that equipartitions every μ i . As it was noted by Pablo Soberón, we may not refer to [9, Theorem 1.3] and use the simpler result of [12] if we lift the measures μ i to the paraboloid \(x_{d+1} = x_{1}^{2}+\cdots+ x_{d}^{2}\) in ℝd+1 and then partition them with a convex generalized Voronoi partition.

Assume without loss of generality that f 1(x) has the largest coefficient at \(\sum_{i=1}^{d} x_{i}^{2}\) among all f j (x). Then the defining equations for C 1 will look like

$$(b_1-b_j)\sum_{i=1}^d x_i^2 + \lambda(x) \le0, $$

where λ(x) is a linear function and b 1−b j is nonnegative. Note that each of these equations defines either a halfspace or a ball and therefore their intersection C 1 is convex.

Now we give a counterexample for d=1 and α not of the form 1/m. Assume \(\frac{1}{n}>\alpha>\frac{1}{n+1}\). Let μ 0 be the uniform measure on (0,1).

Let a i , i=1,…,n, be the points with coordinates \(\frac {i}{n+1}\) and Δ i be the intervals with centers at a i and length \(\epsilon<\alpha-\frac{1}{n+1}\). The support of the measure μ 1 is the union of intervals Δ i and \(\int_{\Delta_{i}}d\mu_{1}=\frac{1}{n}\) for each i (Fig. 1).

Fig. 1
figure 1

Two measures in one dimension

Full size image

It is easy to see that each convex set C with μ 0(C)=α is an interval of length α in intersection with (0,1) and it must contain at least one interval Δ i . Therefore \(\mu_{1}(C)\geq\frac {1}{n}>\alpha\).

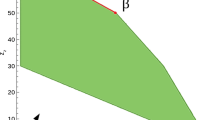
For d>1 we can extend the one-dimensional example. Consider a d-dimensional regular simplex with vertices v 0,v 1,…,v d . Let the measures μ 2,…,μ d concentrate near the vertices v 2,…,v d , respectively. Similarly to the case d=1, let μ 0 be the uniform measure on a small cylinder around the edge v 0 v 1. The measure μ 1 will look like in the one-dimensional case, but its support will be intervals on the segment that connects the centers of faces v 0 v 2…v d and v 1 v 2…v d . See Fig. 2 for the two-dimensional case.

Fig. 2
figure 2

Three measures in two dimensions

Full size image

To conclude the proof we note the following. Assume that the measures μ i are concentrated in δ-neighborhoods of their respective vertices (for i>1) or segments (for i=0,1). Then going to the limit δ→+0 and using the Blaschke selection theorem, we assume that the corresponding C δ tends in the Hausdorff metric to some C 0. This C 0 must intersect the segment [v 0,v 1] by an interval of length at least α|v 0−v 1|. It also has to contain every vertex v i for i=2,…,d. Hence, similarly to the one-dimensional case, C 0 contains in its interior one of the support segments of μ 1. For small enough δ, the convex set C δ will also contain at least 1/n of the measure μ 1, which is a contradiction. □

Remark 6

For d=1 this result follows from the theorem of Levy [10] about a segment on a curve. Note that Hopf [7] showed that the set of α for which the required segment does not exist is additive.

Remark 7

In [4, Theorem 3.2] it was proved that any two absolutely continuous probability measures on S 2 can be cut into pieces of measures α,α,1−2α by a 3-fan. Using the central projection we see that any two absolutely continuous probability measures on ℝ2 may be cut into pieces of measures α,α,1−2α with a (possibly degenerate) 3-fan. It is clear that at least one of the α parts of the fan is a convex angle and therefore Problem 1 has a positive solution for k=d=2 and any α∈(0,1/2].