A Note on Aperiodic Ammann Tiles

Abstract

We present a variant of Ammann tiles consisting of two similar rectilinear hexagons with edge subdivision, which can tile the plane but only in non-periodic ways. A special matching rule, ghost marking, plays a key role in the proof.

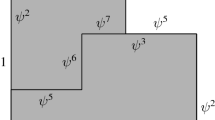
We shall show that the set of tiles in Fig. 1 is aperiodic, that is, it tiles the plane but only in non-periodic way.

Fig. 1

Similar Ammann tiles A and B

Two shapes are similar to each other by the ratio $c=\sqrt{\tau}$ where τ is the golden mean $(1+\sqrt{5})/2$. These shapes belong to the ‘Ammann A2’ family having length parameters. On this choice of length, Grünbaum–Shephard [10] remarked

However it does not seem possible to devise a simple matching condition for these tiles involving markings which are such that the similarity between the tiles extends to markings as well.

and suggested a complicated matching rule including directions and a certain gluing rule of edges to force aperiodicity. Figure 2 shows their markings with edge direction in [10]. Their two tiles have exactly similar markings.

Fig. 2

Markings by Grünbaum–Shephard in [10]

Our marking is a simplification of it, but they are different between two tiles. Markings of edges in Fig. 1 indicate that they are cut at those places, and thus the tile A is treated as a decagon and B an octagon. Our matching rule is simple, we assume that our tiling is edge-to-edge, that is, only the edges of equal lengths can meet in the tiling and they must exactly agree from one end to the other. We prove that this simple matching rule provides aperiodic tiles, regardless of the above quoted remark.

FormalPara Theorem 1

The decagon A and the octagon B form a set of aperiodic tiles.

A tile is a closed polygon in ℝ². Denote by $\mathcal{A}$ a finite set of tiles. A tiling $\mathcal{T}$ of ℝ² is a collection of tiles which covers ℝ² without interior intersections, and each tile is congruent to an element of $\mathcal{A}$ under rigid motion (action of isometry of ℝ²: composition of rotation, translation, and reflection). A tiling $\mathcal{T}$ has a period p∈ℝ² when the tiling exactly matches with its translation by p. A patch of a tiling $\mathcal{T}$ is a finite set of tiles in $\mathcal{T}$ whose union is homeomorphic to a closed ball. A tiling $\mathcal{T}$ is non-periodic if the only period of $\mathcal{T}$ is 0. A set of tiles $\mathcal{A}$ is called aperiodic if $\mathcal{A}$ generates a tiling, but all the tilings generated by $\mathcal{A}$ are non-periodic. To enforce aperiodicity, we often introduce certain matching rules (conditions) on the surfaces of tiles. A well-known example of aperiodic tiles is due to Penrose; it consists of two kinds of tile: kites and darts with matching rules. Ammann gave several sets of aperiodic tiles, one of which is a target of this paper. See [10, 14] for tilings by Penrose, Ammann and more with historical accounts, and [3] for the proof of aperiodicity of Ammann tiles. It had been an open question to give a single tile which forms a set of aperiodic tiles. Recently Socolar-Taylor [16] gave such a hexagonal tile with matching rules. Their matching rules affect non-adjacent tiles but their influence is local. Readers can find further discussion to clarify ambiguities in the definition of number of tiles, periods and matching rules in [17].

The shape in Fig. 1 is rediscovered by Scherer, who considered a dissection of a polygon X into several pieces, all of which is similar to the original X. Seemingly unaware of the result of Ammann, he found a solution ‘Golden Bee’, which is a polygon composed of two similar copies of itself (see Fig. 4). The term ‘Bee’ comes from the shape of the alphabet character ‘b’. Completing the study of Scherer, Schmerl [13] showed that the only polygons that have this property are a right triangle, a $\sqrt{2}:1$ sized parallelogram, or the Golden Bee. See also [2] for a similar question on dissection, assuming that all pieces are similar to each other, but they are not necessarily similar to the original shape.

Our set of tiles consists of two similar rectilinear hexagons in Fig. 1. A counter-clockwise simple closed curve consisting of line segments of lengths c ³, c ², c, 1/c ², 1/c,1 in this order forms a boundary of B and we make turns of right angle at the end points of segments. We turn right at the junction of edges of length 1/c ² and 1/c which forms a dent of B, and turn left at all other corners. The tile B carries two markings within. The markings depicted in B indicate that we deal with this tile as an octagon rather than a hexagon. Thus we consider the length of the edges of B as c,1/c,1,1/c ²,c,1/c ²,1/c,1 in counter-clockwise order where c ³=c+1/c, c ²=1+1/c ². The shape of A is c-times larger than B and A has four markings which cut three edges. So we consider A a decagon of edge lengths 1/c ²,1,1,c,1/c,1,1/c ²,1/c,1,c in counter-clockwise order where c ⁴=1+1+1/c ², c ³=c+1/c and c ²=1+1/c ².

It turned out that there are eight tiles up to translation in this tiling because the right angle rotation does not appear (see Fig. 11).

FormalPara Proof of the Theorem

Hereafter, to avoid description of rigid motion, congruent tiles are not distinguished and designated by the same symbol when there is no room of confusion. An edge of length k is called k-edge.

A standard way to prove non-periodicity of a tiling is to show unique composition property (cf. [3, 10, 19]). Assume, for a given tiling by A and B, there is a unique way to compose them as a super-tiling by tiles cA and cB and also we can repeat this discussion. Then a period p of a tiling must be a period of the super-tiling. Iterating this discussion, the length of p must be smaller than c ⁿ: the diameter of a ball which can be inscribed both in c ⁿ A and in c ⁿ B, which shows p=0. To prove aperiodicity of A and B using unique composition property, we show that all tiling by A and B can be regarded as a tiling by super-tiles cA and cB having exact enlarged matching rules. As a result, we shall show that by this simple marking, the set belongs to the Ammann A2 aperiodic family in the sense of [3], and that all tilings by A and B are non-periodic.

Let us start with the fact that cB=A, discarding markings. We observe that it is impossible to tile the plane only by A. Indeed, the only possibility to fill the dent of A by A is depicted in Fig. 3 by the edge-to-edge condition and the northern remaining part cannot be filled only by A. It is also plain to see that the dent of B is filled only by a suitable reflection of A as in Fig. 4. Therefore a tiling by A and B must contain at least one A and B. For any given tiling by A and B, one can think of the union of B and A in Fig. 4 as a super-tile cA, because its shape is a c times similar extension of A and inherits markings scaled by c with a new marking from the boundary broken line. One marking of A becoming a dent of cA should be erased and we further remove two markings to obtain cA. The remaining A tiles which do not fill the dent of B, can be seen as cB by erasing two markings. See Fig. 5 for the super-tiles cA and cB. We have to show that this removal does no harm. To proceed, let us call these four markings to be removed: ghost markings. We observe that all ghost markings appear at the junction of 1-edge and 1/c ²-edge. Our aim is to show that the set of tilings by cA and cB with ghost markings and the one without them are the same.

Fig. 3

Filling the dent of A by A

Fig. 4

Golden Bee: filling the dent of B

Fig. 5

Super-tiles cA and cB: broken lines indicate 4 ghost markings and the former boundary

Now we come to a technical point of the proof. Note that the influence of removal of a usual marking is intricate, it does not simply mean to relax or to strengthen the matching rule: on one hand we can no longer cut this c ²-edge into a1-edge and 1/c ²-edge at this point, but on the other hand this c ²-edge becomes orientation insensitive and thus c ²-edges may match in two ways. To cope with this logical difficulty, we treat ghost markings in a special way: we admit the freedom to ignore it or to use it to cut the edge. In other words, two edges meeting at a ghost marking can be used as a single c ²-edge or the combination of 1-edge and 1/c ²-edge, as we wish wherever they are, and independently. In short, we may think that ‘ghosts exist or do not exist’ as we like. Under this approach, we have an inclusion $\mathcal{T}_{1}\supset \mathcal{T}_{2}$ where $\mathcal{T}_{1}$ is the set of tilings by cA and cB with ghost markings and $\mathcal{T}_{2}$ is the one without them.¹ We then prove in the sequel that in any tiling in $\mathcal{T}_{1}$, every ghost marking must meet another ghost marking across the edges, which shows that ghost markings are dispensable, i.e., $\mathcal{T}_{1}=\mathcal{T}_{2}$. Once we know this equality, the super-tiling by cA and cB appearing in the previous paragraph surely falls into $\mathcal{T}_{1}$. Thus the proof of unique composition property will be finished.

Pick a tiling of $\mathcal{T}_{1}$. First, we show that ghost markings cannot be used to cut c ²-edges. To see this, it suffices to examine the cases where two 1/c ²-edges meet but their ghost markings do not. There are 10 cases to check, up to symmetry as in Fig. 6. We prove that they do not appear in $\mathcal{T}_{1}$, by showing that they cannot extend to large patches. Indeed, as indicated by black spots, we can either immediately find a corner or dent which cannot be filled, or two corners that we cannot simultaneously fill. Second, we show that there is no tiling in $\mathcal{T}_{1}$ so that two c ²-edges meet but their ghost markings do not match. We check our 10 cases up to symmetry as in Fig. 7 in the similar manner. As the black spots indicate, for nine cases, we can show it in at most two steps. The remaining case without a black spot requires further classification. It is reduced to four configurations in Fig. 8 and in each case we find a dent which cannot be filled. Thus we showed that a tiling in by cA and cB with ghost markings is possible only when ghost markings are not essentially in use, i.e., $\mathcal{T}_{1}\subset \mathcal{T}_{2}$. We have shown the unique composition property.

Fig. 6

Illegal patches of the 1-st kind

Fig. 7

Illegal patches of the 2nd kind

Fig. 8

The remaining case

It remains to show that there exists a tiling by A and B. We have seen that the super-tile cA is subdivided into A and B and cB is made from A in Fig. 5. Let us discard all markings for the moment and consider this Fig. 5 as a substitution rule: giving the images of A and B by the composition of two maps: c-multiplication and subdivision into A and B. We can iterate this c-multiplication subdivision and create patches which spirally grow like Fig. 9. This gives a tiling of the plane by A and B, which is called a fixed point of the substitution rule. We may view this fixed point as a super-tiling by c ³ A and c ³ B with markings indicating the subdivision structure by A and B. Then c ³ A is the composition of three A’s and two B’s, and c ³ B is a composition of two A’s and one B. Boundaries of A and B give natural markings of super-tiles c ³ A and c ³ B as black points in Fig. 10. Confirm that they are exactly located at the c ³ scaled markings of A and B. As the tiling by c ³ A and c ³ B surely exists, we know that there exists a tiling by A and B with the markings scaled down by ratio 1/c ³. Figure 11 gives a patch of tiling by A and B.

Fig. 9

Inflation subdivision

Fig. 10

Markings from c ³ A and c ³ B

Fig. 11

A patch of tiling by A and B

 □

Aperiodic tiles give a good model of quasi-crystals. The diffraction pattern of Penrose tilings shows 10-fold symmetry, which simulates the discovery of quasi-crystals by Shechtman [15]. The reason of 10-fold symmetry is explained from the work of de Bruijn [4, 5], who proved that Penrose tiling is a cut and projection tiling, i.e., its reference points set is the projection of 5-dimensional lattice points in some band. Frettlöh [6] showed that this Ammann tiling is a cut and project tiling as well, and it is an ‘algebraic dual’ of golden triangle tiling (cf. [7–9]). An algorithm for pure discrete tiling dynamics in [1] directly tells the existence of an underlying cut and projection scheme. A nice feature of such aperiodic tiles related to the cut and projection scheme is that local interactions (matching rules) alone force pure point spectrum in diffraction. Therefore it is not necessary to assume a higher-dimensional lattice model within real substances. See [11, 12, 18].

As in [10], Ammann found several markings on A2 family. One of them is a slight modification of A and B, which we call A′ and B′: tile A is shrunk by ratio 1/c to x-axis and B to y-axis. He put several different kinds of marking to have aperiodicity. Figure 12 shows his impressive markings called ‘Ammann bars’ where the segments on A′ and B′ must extend to straight lines across the edges. The tiling by A′ and B′ is a 1/c-shrunk of the one by A and B in one direction. However, for A′ and B′, we do not find edge-to-edge matching rules like A and B which enforce aperiodicity. Our construction is sensitive to the affine transform which changes lengths of the edges.

Fig. 12

Ammann Bars

Our method of ghost markings might apply to situations where all tiles are similar. Especially it is challenging to find a rep-tile so that our method works. Since it is composed of same-sized similar copies of itself, it would produce a single aperiodic tile with edge-to-edge matching rules. However, the author did not find such an example so far.