Batch Coloring of Graphs

Abstract

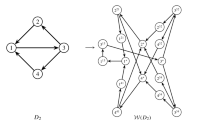
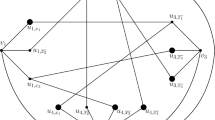
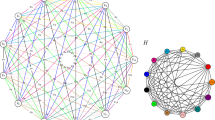
We study two versions of graph coloring, where the goal is to assign a positive integer color to each vertex of an input graph such that adjacent vertices do not receive the same color assignment. For classic vertex coloring, the goal is to minimize the maximum color used, and for the sum coloring problem, the goal is to minimize the sum of colors assigned to all input vertices. In the offline variant, the entire graph is presented at once, and in online problems, one vertex is presented for coloring at each time, and the only information is the identity of its neighbors among previously known vertices. In batched graph coloring, vertices are presented in k batches, for a fixed integer $k \ge 2$, such that the vertices of a batch are presented as a set, and must be colored before the vertices of the next batch are presented. This last model is an intermediate model, which bridges between the two extreme scenarios of the online and offline models. We provide several results, including a general result for sum coloring and results for the classic graph coloring problem on restricted graph classes: We show tight bounds for any graph class containing trees as a subclass (forests, bipartite graphs, planar graphs, and perfect graphs, for example), and an interesting result for interval graphs and $k=2$, where the value of the (strict and asymptotic) competitive ratio depends on whether the graph is presented with its interval representation or not.