On the Complexity of Strongly Connected Components in Directed Hypergraphs

Abstract

We study the complexity of some algorithmic problems on directed hypergraphs and their strongly connected components (Sccs). The main contribution is an almost linear time algorithm computing the terminal strongly connected components (i.e. Sccs which do not reach any components but themselves). Almost linear here means that the complexity of the algorithm is linear in the size of the hypergraph up to a factor α(n), where α is the inverse of Ackermann function, and n is the number of vertices. Our motivation to study this problem arises from a recent application of directed hypergraphs to computational tropical geometry.

We also discuss the problem of computing all Sccs. We establish a superlinear lower bound on the size of the transitive reduction of the reachability relation in directed hypergraphs, showing that it is combinatorially more complex than in directed graphs. Besides, we prove a linear time reduction from the well-studied problem of finding all minimal sets among a given family to the problem of computing the Sccs. Only subquadratic time algorithms are known for the former problem. These results strongly suggest that the problem of computing the Sccs is harder in directed hypergraphs than in directed graphs.

Appendices

Appendix A: An Example of Complete Execution Trace of the Algorithm of Sect. 3

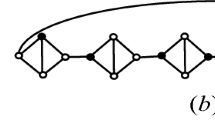
We give the main steps of the execution of the algorithm TerminalScc on the directed hypergraph depicted in Fig. 1:

Vertices are depicted by solid circles if their index is defined, and by dashed circles otherwise. Once a vertex is placed into Finished, it is depicted in gray. Similarly, a hyperarc which has never been placed into a local stack F is represented by dotted lines. Once it is pushed into F, it becomes solid, and when it is popped from F, it is colored in gray (note that for the sake of readability, gray hyperarcs mapped to trivial cycles after a vertex merging step will not be represented). The stack F which is mentioned always corresponds to the stack local to the last non-terminated call of the function Visit.

Initially, Find(z)=z for all z∈{u,v,w,x,y,t}. We suppose that Visit(u) is called first. After the execution of the block from Lines 18 to 35, the current state is:

Following the hyperarc a ₁, Visit(v) is called during the execution of the block from Lines 36 to 48 of Visit(u). After Line 35 in Visit(v), the root of the hyperarc a ₄ is set to v, and the counter $c_{a_{4}}$ is incremented to 1 since v∈S. The state is:

Similarly, the function Visit(w) is called during the execution of the loop from Lines 36 to 48 in Visit(v). After Line 35 in Visit(w), the root of the hyperarc a ₅ is set to w, and the counter $c_{a_{5}}$ is incremented to 1 since w∈S. Besides, $c_{a_{4}}$ is incremented to 2=|T(a ₄)| since $\textsc{Find}{(r_{a_{4}})} = \textsc{Find}{(v)} = v \in S$, so that a ₄ is pushed on the stack F _v . The state is:

The execution of the loop from Lines 36 to 48 of Visit(w) discovers that index[u] is defined but u∉Finished, so that low[w] is set to min(low[w],low[u])=0 and $\mathit{is\_term}[w]$ to $\mathit{is\_term}[w] \And\mathit{is\_term}[u] = \mathit{true}$. At the end of the loop, the state is therefore:

Since low[w]≠index[w], the block from Lines 49 to 65 is not executed, and Visit(w) terminates. Back to the loop from Lines 36 to 48 in Visit(v), low[v] is assigned to the value min(low[v],low[w])=0, and $\mathit{is\_term}[v]$ to $\mathit {is\_term}[v] \And\mathit{is\_term}[w] = \mathit{true}$:

Since low[v]≠index[v], the block from Lines 49 to 65 is not executed, and Visit(v) terminates. Back to the loop from Lines 36 to 48 in Visit(u), low[u] is assigned to the value min(low[u],low[v])=0, and $\mathit{is\_term}[u]$ to $\mathit {is\_term}[u] \And\mathit{is\_term}[v] = \mathit{true}$. Therefore, at Line 49, the conditions low[u]=index[u] and $\mathit{is\_term}[u] = \mathit{true}$ hold, so that a vertex merging step is executed. At that point, the stack F is empty. After that, i is set to index[u]=0 (Line 51), and F _u =[ ] is emptied to F (Line 52), so that F is still empty. Then w is popped from S, and since index[w]=2>i=0, the loop from Lines 54 to 58 is iterated. Then the stack F _w =[ ] is emptied in F. At Line 56, Merge(u,w) is called. The result is denoted by U (in practice, either U=u or U=w). The state is:

Then v is popped from S, and since index[v]=1>i=0, the loop Lines 54 to 58 is iterated again. Then the stack F _v =[a ₄] is emptied in F. At Line 56, Merge(U,v) is called. The result is set to U (in practice, U is one of the vertices u, v, w). The state is:

After that, u is popped from S, and as index[u]=0=i, the loop is terminated. At Line 59, index[U] is set to i, and U is pushed on S. Since F≠∅, we go back to Line 36, in the state:

Then a ₄ is popped from F, and the loop from 38 to 47 iterates over H(a ₄)={x,y}. Suppose that x is treated first. Then Visit(x) is called. During its execution, at Line 35, the state is:

Since F is empty, the loop from Lines 36 to 48 is not executed. At Line 49, low[x]=index[x] and $\mathit{is\_ term}[x] = \mathit{true}$, so that a trivial vertex merging step is performed, only on x, since it is the top element of S. After Line 59, it can be verified that S=[x;U], index[x]=3 and F=[ ]. Therefore, the goto statement at Line 60 is not executed. It follows that the loop from Lines 62 to 64 is executed, and after that, the state is:

After the termination of Visit(x), since x∈Finished, $\mathit{is\_term}[U]$ is set to false. After that, Visit(y) is called, and at Line 35, it can be checked that $c_{a_{5}}$ has been incremented to 2=|T(a ₅)| because $R_{a_{5}} = \textsc{Find}{(r_{a_{5}})} = \textsc{Find}{(w)} = U$ and U∈S. Therefore, a ₅ is pushed to F _U , and the state is:

As for the vertex x, Visit(y) terminates by popping y from S and adding it to Finished. Back to the execution of Visit(U), at Line 49, the state is:

While low[U]=index[U], $\mathit{is\_term}[U]$ is equal to false, so that no vertex merging loop is performed on U. Therefore, a ₅ is not popped from F _U . Nevertheless, the loop from Lines 62 to 64 is executed, and after that, Visit(u) is terminated in the state:

Finally, Visit(t) is called from TerminalScc at Line 13. It can be verified that a trivial vertex merging loop is performed on t only. After that, t is placed into Finished. Therefore, the final state of TerminalScc is:

As $\mathit{is\_term}[x] = \mathit{is\_term}[y] = \mathit{is\_ term}[t] = \mathit{true}$ and $\mathit{is\_term}[\textsc{Find} {(z)}] = \mathit{false}$ for z=u,v,w, there are three terminal Sccs, given by the sets:

Appendix B: Proof of Theorem 5

The correctness proof of the algorithm TerminalScc turns out to be harder than for algorithms on directed graphs such as Tarjan’s one [38], due to the complexity of the invariants which arise in the former algorithm. That is why we propose to show the correctness of two intermediary algorithms, named TerminalScc2 (Fig. 6) and TerminalScc3 (Fig. 7), and then to prove that they are equivalent to TerminalScc.

Fig. 6

First intermediary form of our algorithm computing the terminal Sccs

Fig. 7

Second intermediary form of our algorithm computing the terminal Sccs

The main difference between the first intermediary form and TerminalScc is that it does not use auxiliary data associated to the hyperarcs to determine which ones are added to the digraph $\mathsf{graph} (\mathcal{H}_{\mathit{cur}})$ after a vertex merging step. Instead, the stack F is directly filled with the right hyperarcs (Lines 24 and 51). Besides, a boolean $\mathit{no\_merge}$ is used to determine whether a vertex merging step has been executed. The notion of vertex merging step is refined: it now refers to the execution of the instructions between Lines 43 and 52 in which the boolean $\mathit{no\_merge}$ is set to false.

For the sake of simplicity, we will suppose that sequences of assignment or stack manipulations are executed atomically. For instance, the sequences of instructions located in the blocks from Lines 18 and 27, or from Lines 43 and 52, and at from Lines 58 to 60, are considered as elementary instructions. Under this assumption, intermediate complex invariants do not have to be considered.

We first begin with very simple invariants:

Invariant 1

Let U be a vertex of the current hypergraph $\mathcal{H}_{\mathit{cur}}$. Then index[U] is defined if, and only if, index[u] is defined for all $u \in\mathcal{V}$ such that Find(u)=U.

Proof

It can be shown by induction on the number of vertex merging steps which has been performed on U.

In the basis case, there is a unique element $u \in\mathcal{V}$ such that Find(u)=U. Besides, U=u, so that the statement is trivial.

After a merging step yielding the vertex U, we necessarily have index[U]≠undef. Moreover, all the vertices V which has been merged into U satisfied index[V]≠undef because they were stored in the stack S. Applying the induction hypothesis terminates the proof. □

Invariant 2

Let $u \in\mathcal{V}$. When index[u] is defined, then Find(u) belongs either to the stack S, or to the set Finished (both cases cannot happen simultaneously).

Proof

Initially, Find(u)=u, and once index[u] is defined, Find(u) is pushed on S (Line 22). Naturally, u∉Finished, because otherwise, index[u] would have been defined before (see the condition Line 60). After that, U=Find(u) can be popped from S at three possible locations:

• at Lines 44 or 48, in which case U is transformed into a vertex U′ which is immediately pushed on the stack S at Line 50. Since after that, Find(u)=U′, the property Find(u)∈S still holds.

• at Line 59, in which case it is directly appended to the set Finished.

 □

Invariant 3

The set Finished is always growing.

Proof

Once an element is added to Finished, it is never removed from it nor merged into another vertex (the function Merge is always called on elements immediately popped from the stack S). □

Proposition 18

After the algorithm $\textsc{TerminalScc2}{(\mathcal{H})}$ terminates, the sets $\{ v \in\mathcal{V}\mid\textsc{Find}{(v)} = U \textit{ and } \mathit {is\_term}[U] = \mathit{true} \}$ are precisely the terminal Scc s of $\mathcal{H}$.

Proof

We prove the whole statement by induction on the number of vertex merging steps.

Basis Case. First, suppose that the hypergraph $\mathcal{H}$ is such that no vertices are merged during the execution of TerminalScc2($\mathcal{H}$), i.e. the vertex merging loop (from Lines 45 to 49) is never executed. Then the boolean $\mathit{no\_merge}$ is always set to true, so that n is never redefined to i+1 (Line 54), and there is no back edge to Line 28 in the control-flow graph. It follows that removing all the lines between Lines 43 to 55 does not change the behavior of the algorithm. Besides, since the function Merge is never called, Find(u) always coincides with u. Finally, at Line 24, F is precisely assigned to the set of simple hyperarcs leaving u in $\mathcal{H}$, so that the loop from Lines 28 to 40 iterates on the successors of u in $\mathsf {graph}(\mathcal{H} )$. As a consequence, the algorithm TerminalScc2($\mathcal{H}$) behaves exactly like TerminalScc($\mathsf{graph}(\mathcal {H})$). Moreover, under our assumption, the terminal Sccs of $\mathsf {graph}(\mathcal{H})$ are all reduced to singletons (otherwise, the loop from Lines 45 to 49 would be executed, and some vertices would be merged). Therefore, by Proposition 2, the statement in Proposition 18 holds.

Inductive Case. Suppose that the vertex merging loop is executed at least once, and that its first execution happens during the execution of, say, Visit2(x). Consider the state of the algorithm at Line 43 just before the execution of the first occurrence of the vertex merging step. Until that point, Find(v) is still equal to v for all vertices $v \in \mathcal{V}$, so that the execution of TerminalScc($\mathcal {H}$) coincides with the execution of TerminalScc($\mathsf{graph}(\mathcal{H})$). Consequently, if C is the set formed by the vertices y located above x in the stack S (including x), C forms a terminal Scc of $\mathsf{graph}(\mathcal{H})$. In particular, the elements of C are located in a same Scc of the hypergraph $\mathcal{H}$.

Consider the hypergraph $\mathcal{H}'$ obtained by merging the elements of C in the hypergraph $(\mathcal{V},A \setminus\{ a \mid\exists y \in C \text{ s.t. } T(a) = \{ y \} \})$, and let X be the resulting vertex. For now, we may add a hypergraph as last argument of the functions Visit2, Find, etc., to distinguish their execution in the context of the call to TerminalScc2($\mathcal{H}$) or TerminalScc2($\mathcal{H}'$). We make the following observations:

• the vertex x is the first element of the component C to be visited during the execution of TerminalScc2($\mathcal{H}$). It follows that the execution of TerminalScc2($\mathcal{H}$) until the call to Visit2($x,\mathcal{H}$) coincides with the execution of TerminalScc2($\mathcal{H}'$) until the call to Visit2($X,\mathcal{H}'$).

• besides, during the execution of Visit2($x,\mathcal{H}$), the execution of the loop from Lines 28 to 40 only has a local impact, i.e. on the $\mathit{is\_term}[y]$, index[y], or low[y] for y∈C, and not on any information relative to other vertices. Indeed, we claim that the set of the vertices y on which Visit2 is called during the execution of the loop is exactly C∖{x}. First, for all y∈C∖{x}, Visit2(y) has necessarily been executed after Line 28 (otherwise, by Invariant 2, y would be either below x in the stack S, or in Finished). Conversely, suppose that after Line 28, there is a call to Visit2(t) with t∉C. By Invariant 2, t belongs to Finished, so that for one of the vertices w examined in the loop, either w∈Finished or $\mathit{is\_ term}[w] = \mathit{false}$ after the call to Visit2(w). Hence $\mathit{is\_term}[x]$ should be false, which contradicts our assumptions.

• finally, from the execution of Line 55 during the call to Visit2($x,\mathcal{H}$), our algorithm behaves exactly as TerminalScc2($\mathcal{H}'$) from the execution of Line 28 in Visit2($X,\mathcal{H}'$). Indeed, index[X] is equal to i, and the latter is equal to n−1. Similarly, for all y∈C, low[y]=i and $\mathit{is\_term}[y] = \mathit{true}$. The vertex X being equal to one of the y∈C, we also have low[X]=i and $\mathit{is\_term}[X] = \mathit{true}$. Moreover, X is the top element of S.

  Furthermore, it can be verified that at Line 51, the set F contains exactly all the hyperarcs of A which generate the simple hyperarcs leaving X in $\mathcal{H}'$: they are exactly characterized by

  

  since at that Line 51, a hyperarc a satisfies collected _a =true if, and only if, T(a) is reduced to a singleton {t} such that index[t] is defined.

  Finally, for all vertices y∈C, $\textsc{Find}{(y,\mathcal{H})}$ can be equivalently replaced by $\textsc{Find}{(X,\mathcal{H}')}$.

As a consequence, TerminalScc2($\mathcal{H}$) and TerminalScc2($\mathcal{H}'$) return the same result. Both functions perform the same union-find operations, except the first the vertex merging step executed by TerminalScc2($\mathcal{H}$) on C.

Let f be the function which maps all vertices y∈C to X, and any other vertex to itself. We claim that $\mathcal{H}'$ and $f(\mathcal{H})$ have the same reachability graph, i.e. $\rightsquigarrow_{\mathcal {H}'}$ and $\rightsquigarrow _{f(\mathcal{H})}$ are identical relations. Indeed, the two hypergraphs only differ on the images of the hyperarcs a∈A such that T(a)={y} for some y∈C. For such hyperarcs, we have H(a)⊆C, because otherwise, $\mathit{is\_term}[x]$ would have been set to false (i.e. the component C would not be terminal). It follows that their are mapped to the cycle ({X},{X}) by f, so that $\mathcal{H}'$ and $f(\mathcal{H} )$ clearly have the same reachability graph. In particular, they have the same terminal Sccs.

Finally, since the elements of C are in a same Scc of $\mathcal{H}$, Proposition 3 shows that the function f induces a one-to-one correspondence between the Sccs of $\mathcal {H}$ and the Sccs of $f(\mathcal{H})$:

The action of the function f exactly corresponds to the vertex merging step performed on C. Since by induction hypothesis, TerminalScc2($\mathcal{H}'$) determines the terminal Sccs in $f(\mathcal{H})$, it follows that Proposition 18 holds. □

The second intermediary version of our algorithm, TerminalScc3, is based on the first one, but it performs the same computations on the auxiliary data r _a and c _a as in TerminalScc. However, the latter are never used, because at Line 64, F is re-assigned to the value provided in TerminalScc2. It follows that for now, the parts in gray can be ignored. The following lemma states that TerminalScc2 and TerminalScc3 are equivalent:

Proposition 19

Let $\mathcal{H}$ be a directed hypergraph. After the execution of $\textsc {TerminalScc3}{(\mathcal{H})}$, the sets $\{ v \in\mathcal{V}\mid \textsc{Find}{(v)} = U \textit{ and } \mathit{is\_term}[U] = \mathit{true}\}$ precisely correspond to the terminal Scc s of $\mathcal{H}$.

Proof

When Visit3(u) is executed, the local stack F is not directly assigned to the set {a∈A∣T(a)={u}} (see Line 24 in Fig. 6), but built by several iterations on the set A _u (Line 25). Since u∈T(a) and |T(a)|=1 holds if, and only if, T(a) is reduced to {u}, Visit3(u) initially fills F with the same hyperarcs as Visit2(u).

Besides, the condition $\mathit{no\_merge}= \mathit{false}$ in Visit2 (Line 53) is replaced by F≠∅ (Line 66). We claim that the condition F≠∅ can be safely used in Visit2 as well. Indeed, in Visit2, F≠∅ implies $\mathit {no\_merge} = \mathit{false}$. Conversely, suppose that in Visit2, $\mathit{no\_merge}= \mathit{false}$ and F=∅, so that the algorithm goes back to Line 55 after having $\mathit{no\_merge}$ to true. The loop from Lines 28 to 40 is not executed since F=∅, and it directly leads to a new execution of Lines 41 to 53 with $\mathit{no\_merge}= \mathit{true}$. Therefore, going back to Line 55 was useless.

Finally, during the vertex merging step in Visit3, n keeps its value, which is greater than or equal to i+1, but is not necessarily equal to i+1 like in Visit2 (just after Line 54). This is safe because the whole algorithm only need that n take increasing values, and not necessarily consecutive ones.

We conclude by applying Proposition 18. □

We make similar assumptions on the atomicity of the sequences of instructions. Note that Invariant 1, 2, and 3 still holds in Visit3.

Invariant 4

Let a∈A such that |T(a)|>1. If for all x∈T(a), index[x] is defined, then the root r _a is defined.

Proof

For all x∈T(a), Visit3(x) has been called. The root r _a has necessarily been defined at the first of these calls (remember that the block from Lines 19 to 39 is supposed to be executed atomically). □

Invariant 5

Consider a state cur of the algorithm in which U∈Finished. Then any vertex reachable from U in $\mathsf{graph}(\mathcal {H}_{\mathit{cur}})$ is also in Finished.

Proof

The invariant clearly holds when U is placed in Finished. Using the atomicity assumptions, the call to Visit3(u) is necessarily terminated. Let old be the state of the algorithm at that point, and $\mathcal{H}_{\mathit{old}}$ and Finished _old the corresponding hypergraph and set of terminated vertices at that state respectively. Since Visit3(u) has performed a depth-first search from the vertex U in $\mathsf{graph}(\mathcal{H}_{\mathit{old}})$, all the vertices reachable from U in $\mathcal{H} _{\mathit{old}}$ stand in Finished _old .

We claim that the invariant is then preserved by the following vertex merging steps. The graph arcs which may be added by the latter leave vertices in S, and consequently not from elements in Finished (by Invariant 2). It follows that the set of reachable vertices from elements of Finished _old is not changed by future vertex merging steps. As a result, all the vertices reachable from U in $\mathsf{graph}(\mathcal{H}_{\mathit{cur}})$ are elements of Finished _old . Since by Invariant 5, Finished _old ⊆Finished, this proves the whole invariant in the state cur. □

Invariant 6

In the digraph $\mathsf{graph}(\mathcal{H}_{\mathit{cur}})$, at the call to Visit3(u), u is reachable from a vertex W such that index[W] is defined if, and only if, W belongs to the stack S.

Proof

The “if” part can be shown by induction. When the function Visit3(u) is called from Line 14, the stack S is empty, so that this is obvious. Otherwise, it is called from Line 44 during the execution of Visit3(x). Then X=Find(x) is reachable from any vertex in the stack, since x was itself reachable from any vertex in the stack at the call to Find(X) (inductive hypothesis) and that this reachability property is preserved by potential vertex merging steps (Proposition 3). As u is obviously reachable from X, this shows the statement.

Conversely, suppose that index[W] is defined, and W is not in the stack. According to Invariant 2, W is necessarily an element of Finished. Hence u also belongs to Finished by Invariant 5, which is a contradiction since this cannot hold at the call to Visit(u). □

Invariant 7

Let a∈A such that |T(a)|>1. Consider a state cur of the algorithm TerminalScc3 in which r _a is defined.

Then c _a is equal to the number of elements x∈T(a) such that index[x] is defined and Find(x) is reachable from Find(r _a ) in $\mathsf{graph}(\mathcal{H}_{\mathit{cur}})$.

Proof

Since at Line 30, c _a is incremented only if R _a =Find(r _a ) belongs to S, we already know using Invariant 6 that c _a is equal to the number of elements x∈T(a) such that, at the call to Visit3(x), x was reachable from Find(r _a ).

Now, let $x \in\mathcal{V}$, and consider a state cur of the algorithm in which r _a and index[x] are both defined, and Find(r _a ) appears in the stack S. Since index[x] is defined, Visit3 has been called on x, and let old be the state of the algorithm at that point. Let us denote by $\mathcal{H}_{\mathit{old}}$ and $\mathcal{H}_{\mathit{cur}}$ the current hypergraphs at the states old and cur respectively. Like previously, we may add a hypergraph as last argument of the function Find to distinguish its execution in the states old and cur. We claim that $\textsc {Find}{(r_{a},\mathcal{H}_{\mathit{cur}})} \rightsquigarrow _{\mathsf{graph}(\mathcal{H}_{\mathit{cur}})} \textsc{Find}{(x,\mathcal {H}_{\mathit{cur}})}$ if, and only if, $\textsc{Find} {(r_{a},\mathcal{H}_{\mathit{old}})} \rightsquigarrow_{\mathsf {graph}(\mathcal{H}_{\mathit{old}})} x$. The “if” part is due to the fact that reachability in $\mathsf{graph}(\mathcal {H}_{\mathit{old}})$ is not altered by the vertex merging steps (Proposition 3). Conversely, if x is not reachable from $\textsc{Find}{(r_{a},\mathcal {H}_{\mathit{old}})}$ in $\mathcal{H}_{\mathit{old}}$, then $\textsc{Find}{(r_{a},\mathcal {H}_{\mathit{old}})}$ is not in the call stack S _old (Invariant 6), so that it is an element of Finished _old . But Finished _old ⊆Finished _cur , which contradicts our assumption since by Invariant 2, an element cannot be stored in Finished _cur and S _cur at the same time. It follows that if r _a is defined and Find(r _a ) appears in the stack S, c _a is equal to the number of elements x∈T(a) such that index[x] is defined and $\textsc{Find} {(r_{a})} \rightsquigarrow_{\mathsf{graph}(\mathcal{H}_{\mathit{cur}})} \textsc{Find}{(x)}$.

Let cur be the state of the algorithm when Find(r _a ) is moved from S to Finished. The invariant still holds. Besides, in the future states new, c _a is not incremented because $\textsc {Find}{(r_{a}, \mathcal{H}_{\mathit{cur}})} \in\mathit{Finished}_{\mathit{cur}}\subseteq\mathit{Finished}_{\mathit{new}}$ (Invariant 3), so that $\textsc{Find}{(r_{a},\mathcal{H}_{\mathit{new}})} = \textsc{Find}{(r_{a}, \mathcal{H}_{\mathit{cur}}) }$, and the latter cannot appear in the stack S _new (Invariant 2). Furthermore, any vertex reachable from $R_{a} = \textsc{Find} {(r_{a},\mathcal{H}_{\mathit{new}})}$ in $\mathsf{graph}(\mathcal {H}_{\mathit{new}})$ belongs to Finished _new (Invariant 5). It even belongs to Finished _cur , as shown in the second part of the proof of Invariant 5 (emphasized sentence). It follows that the number of reachable vertices from Find(r _a ) has not changed between states cur and new. Therefore, the invariant on c _a will be preserved, which completes the proof. □

Proposition 20

In Visit3, the assignment at Line 64 does not change the value of F.

Proof

It can be shown by strong induction on the number p of times that this line has been executed. Suppose that we are currently at Line 55, and let X ₁,…,X _q be the elements of the stack located above the root U=X ₁ of the terminal Scc of $\mathsf{graph}(\mathcal{H}_{\mathit{cur}})$. Any arc a which will transferred to F from Line 55 to Line 62 satisfies c _a =|T(a)|>1 and Find(r _a )=X _i for some 1≤i≤q (since at 55, F is initially empty). Invariant 7 implies that for all elements x∈T(a), Find(x) is reachable from X _i in $\mathsf{graph}(\mathcal{H}_{\mathit{cur}})$, so that by terminality of the Scc C={X ₁,…,X _q }, Find(x) belongs to C, i.e. there exists j such that Find(x)=X _j . It follows that at Line 62, Find(x)=U for all x∈T(a). Then, we claim that collected _a =false at Line 62. Indeed, a′∈A satisfies collected _a′=true if, and only if:

• either it has been copied to F at Line 25, in which case |T(a′)|=1,

• or it has been copied to F at the r-th execution of Line 64, with r<p. By induction hypothesis, this means that a′ has been pushed on a stack F _X and then popped from it strictly before the r-th execution of Line 64.

Observe that a given hyperarc can be popped from a stack F _x at most once during the whole execution of TerminalScc3. Here, a has been popped from $F_{X_{i}}$ after the p-th execution of Line 64, and |T(a)|>1. It follows that collected _a =false.

Conversely, suppose for that, at Line 64, collected _a =false, and all the x∈T(a) satisfies Find(x)=U. Clearly, |T(a)|>1 (otherwise, a would have been placed into F at Line 25 and collected _a would be equal to true). Few steps before, at Line 55, Find(x) is equal to one of X _j , 1≤j≤q. Since index[X _j ] is defined (X _j is an element of the stack S), by Invariant 1, index[x] is also defined for all x∈T(a), hence, the root r _a is defined by Invariant 4. Besides, Find(r _a ) is equal to one of the X _j , say X _k (since r _a ∈T(a)). As all the Find(x) are reachable from Find(r _a ) in $\mathsf{graph}(\mathcal {H}_{\mathit{cur}})$, then c _a =|T(a)| using Invariant 7. It follows that a has been pushed on the stack $F_{R_{a}}$, where $R_{a} = \textsc {Find}{(r_{a},\mathcal{H}_{\mathit{old}}) }$ in an previous state old of the algorithm. As collected _a =false, a has not been popped from $F_{R_{a}}$, and consequently, the vertex R _a of $\mathcal{H}_{\mathit{old}}$ has not involved in a vertex merging step. Therefore, R _a is still equal to $\textsc{Find}{(r_{a},\mathcal {H}_{\mathit{cur}})} = X_{k}$. It follows that at Line 55, a is stored in $F_{X_{k}}$, and thus it is copied to F between Lines 55 and 62. This completes the proof. □

We now can prove the correctness of TerminalScc.

Proof of Theorem 5

By Proposition 20, Line 64 can be safely removed in Visit3. It follows that the booleans collected _a are now useless, so that Line 5, the loop from Lines 37 to 39, and Line 65 can be also removed. After that, we precisely obtain the algorithm TerminalScc. Proposition 19 completes the proof. □