Abstract
We prove that the extremal process of branching Brownian motion, in the limit of large times, converges weakly to a cluster point process. The limiting process is a (randomly shifted) Poisson cluster process, where the positions of the clusters is a Poisson process with intensity measure with exponential density. The law of the individual clusters is characterized as branching Brownian motions conditioned to perform “unusually large displacements”, and its existence is proved. The proof combines three main ingredients. First, the results of Bramson on the convergence of solutions of the Kolmogorov–Petrovsky–Piscounov equation with general initial conditions to standing waves. Second, the integral representations of such waves as first obtained by Lalley and Sellke in the case of Heaviside initial conditions. Third, a proper identification of the tail of the extremal process with an auxiliary process (based on the work of Chauvin and Rouault), which fully captures the large time asymptotics of the extremal process. The analysis through the auxiliary process is a rigorous formulation of the cavity method developed in the study of mean field spin glasses.
Similar content being viewed by others
1 Introduction
Branching Brownian motion (BBM) is a continuous-time Markov branching process which plays an important role in the theory of partial differential equations [9, 10, 32, 37], in the theory of disordered systems [13, 15, 26], and in biology [29]. It is constructed as follows.
Start with a single particle which performs standard Brownian motion \(x(t)\) with \(x(0)=0\), which it continues for an exponential holding time \(T\) independent of \(x\), with \(\mathbb{P }\left[ T > t\right] = \mathrm{e}^{-t}\). At time \(T\), the particle splits independently of \(x\) and \(T\) into \(k\) offspring with probability \(p_k\), where \(\sum _{k=1}^\infty p_k = 1\), \(\sum _{k=1}^\infty k p_k = 2\), and \(K \equiv \sum _{k} k(k-1) p_k < \infty \). These particles continue along independent Brownian paths starting at \(x(T)\), and are subject to the same splitting rule, with the effect that the resulting tree \(\mathfrak X \) contains, after an elapsed time \(t>0\), \(n(t)\) particles located at \(x_1(t), \dots , x_{n(t)}(t)\), with \(n(t)\) being the random number of particles generated up to that time. It holds that \(\mathbb{E }n(t)=e^t\).
The link between BBM and partial differential equations is provided by the following observation due to McKean [37]: if one denotes by
the law of the maximal displacement, a renewal argument shows that \(v(t,x)\) solves the Kolmogorov–Petrovsky–Piscounov or Fisher [F-KPP] equation,
with Heaviside initial condition
The F-KPP equation admits traveling waves: there exists a unique solution satisfying
with the centering term given by
and \(\omega (x)\) the distribution function which solves the o.d.e.
If one excludes the trivial cases, solutions to (1.6) are unique up to translations: this will play a crucial role in our considerations.
Lalley and Sellke [33] provided a characterization of the limiting law of the maximal displacement in terms of a random shift of the Gumbel distribution. More precisely, denoting by
the so-called derivative martingale, Lalley and Sellke proved that \(Z(t)\) converges almost surely to a strictly positive random variable \(Z\), and established the integral representation
for some \(C>0\).
It is also known (see e.g. Bramson [16] and Harris [30]) that
Despite the precise information on the maximal displacement of BBM, an understanding of the full statistics of the particles close to the maximal one has been lacking. The statistics of such particles are fully encoded in the extremal process, namely the random measure
The main result of this paper is an explicit construction of the extremal process in the limit of large times.
2 Main result
The description of the limiting extremal process has two parts: the cluster-extrema, and the clusters.
-
The cluster-extrema. Let \(Z\) be the limiting derivative martingale. Conditionally on \(Z\), we consider the Poisson point process (PPP) on \(\mathbb{R }\) of intensity \(C Z \sqrt{2}\mathrm{e}^{-\sqrt{2}x} \text{ d}x\):
$$\begin{aligned} \mathcal P _Z\equiv \sum _{i\in \mathbb{N }}\delta _{p_i} \stackrel{\text{ law}}{=}\text{ PPP}\left(C Z \sqrt{2}\mathrm{e}^{-\sqrt{2}x} \text{ d}x \right)\!, \end{aligned}$$(2.1)with \(C\) as in (1.8).
-
The clusters. Consider the extremal process shifted by \(\sqrt{2}{t}\) instead of \(m(t)\):
$$\begin{aligned} \overline{\mathcal{E }}_t= \sum _{k\le n(t)} \delta _{x_k(t)-\sqrt{2}t}. \end{aligned}$$(2.2)Obviously, the limit of such a process must be trivial, since in view of (1.5), the probability that the maximum of BBM shifted by \(-\sqrt{2}t\) does not drift to \(-\infty \) is vanishing in the large time limit. It however turns out, see Theorem below, that conditionally on the event \(\{\max _{k} x_k(t) -\sqrt{2} t \ge 0\}\), the process \(\overline{\mathcal{E }}_t\) does converge to a well defined point process \( \overline{\mathcal{E }}=\sum _{j}\delta _{\xi _j}\) in the limit of large times. We may then define the point process of the gaps
$$\begin{aligned} \mathcal D =\sum _j \delta _{\Delta _j},\quad \Delta _j \equiv \xi _j - \max _i \xi _i. \end{aligned}$$(2.3)Note that \(\mathcal D \) is a point process on \((\infty ,0]\) with an atom at \(0\).
Theorem 2.1
(Main Theorem) Let \(\mathcal P _Z\) be as in (2.1) and let \(\left\{ \mathcal{D }^{(i)}, i\in \mathbb{N }\right\} \) be a family of independent copies of the gap-process (2.3). Then the point process \(\mathcal E _t = \sum _{k\le n(t)} \delta _{x_k(t) -m(t)}\) converges in law as \(t\rightarrow \infty \) to a Poisson cluster point process \(\mathcal E \) given by
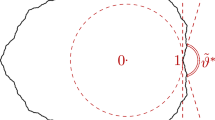
A graphical depiction is given in Fig. 1 below.
Given the inherent self-similarity of BBM, it can hardly come as a surprise that the extremal process of BBM in the limit of large times is fractal-like. As such, it has a number of interesting properties (e.g. the invariance under superpositions, see Corollary 3.3, or the representation of the clusters in terms of BBM with drift, see Remark 3.5).
Understanding the extremal process of BBM in the limit \(t\rightarrow \infty \) has been a long-standing problem of fundamental interest. Most classical results for extremal processes of correlated random variables concern criteria to prove that the behavior is the same as for i.i.d. variables [34]. Bramson’s result shows that this cannot be the case for BBM. A class of models where a more complex structure of Poisson cascades was shown to emerge are the generalized random energy models of Derrida [13, 14, 25]. These models, however, have a rather simple hierarchical structure involving only a finite number of hierarchies which greatly simplifies the analysis, which cannot be carried over to models with infinite levels of branching such as BBM or the continuous random energy models studied in [15]. BBM is a case right at the borderline where correlations just start to effect the extremes and the structure of the extremal process. Results on the extremes of BBM allow one to peek into the world beyond the simple Poisson structures and hopefully open the gate towards the rigorous understanding of complex extremal structures.
Mathematically, BBM offers a spectacular interplay between probability and non-linear p.d.e’s, as was noted already by McKean [37]. On one hand, the proof of Theorem 2.1 will rely on this dual aspect, in particular on precise estimates of the solutions of the F-KPP equations based on those of Bramson [16, 17] and of Chauvin and Rouault [21], see Sect. 3.1. This aspect of the paper is in the spirit of Derrida and Spohn [26] who studied the free energy of the model by relying on results on the F-KPP equation. On the other hand, we propose a new method to study the extremal statistics of BBM based on the introduction of an auxiliary point process, whose correlation structure is much simpler than the one of BBM. As explained in Sect. 3.2, this approach finds its origins in the cavity method in spin glasses [41] and in the study of competing particle systems [3, 39].
We believe this heuristic is a potentially powerful tool to understand other problems in extreme value statistics of correlated variables.
Finally, we remark that a structure similar to the one depicted in Theorem 2.1 is expected to emerge in all the models which are conjectured to fall into the universality class of branching Brownian motion, such as the 2-dim Gaussian Free Field (2DGFF) [11, 12, 18], or the cover time for the simple random walk on the two dimensional discrete torus [23, 24]. These are models whose correlations decay logarithmically with the distance. In particular, for log-correlated Gaussian field like the 2DGFF, we conjecture that the extremal process properly re-centered exists and is exactly of the form (2.4). Namely, the statistics of well-separated high points should be Poissonian with intensity measure with exponential density. In particular, the law of the maximum should be a mixture of a Gumbel as in (1.8) (after this paper has been submitted, partial progress towards this conjecture has been achieved in [27], and [28]). Finally, the law of the clusters should be the one of a 2DGFF conditioned to be unusually high (that is, with maximal displacement of the order of \(c\log N\), for the appropriate constant \(c\), without a \(\log \log N\) correction, where \(N\) is the number of variables).
2.1 Relation to recent works
Many results have appeared in the past few years that shed light on the distribution of the particles of BBM close to the maximum in the limit of large times.
On the physics literature side, we mention the contributions of Brunet and Derrida [19, 20], who reduce the problem of the statistical properties of particles at the edge of BBM to that of identifying the finer properties of the delay of travelling waves (here and below, “edge” stands for the set of particles which are at distances of order one from the maximum).
On the mathematics side, properties of the large time limit of the extremal process have been established in two papers of ours [5, 6]. In the first paper we obtained a precise description of the paths of extremal particles which in turn imply a somewhat surprising restriction of the correlations of particles at the edge of BBM. These results were instrumental in the second paper where it is proved that a certain process obtained by a correlation-dependent thinning of the extremal particles converges to a random shift of a Poisson Point Process (PPP) with intensity measure with exponential density. The approach differs from the one used here to prove the Poissonian statistics of the cluster-extrema. There, the proof relied heavily on the description of the paths of extremal particles developed in [5], and did not prove that clusters are identically distributed, and describing their law. The approach based on the auxiliary point process fills this gap.
A description of the extremal process in terms of a Poisson cluster process has also been obtained independently by Aïdekon et al. [2] shortly after the first version of this paper appeared on arXiv. Their approach is based in part on a precise control of the localization of the paths of extremal particles that are essentially the ones of [5], cf. Proposition 2.5 in [2] and Theorems 2.2, 2.3 and 2.5 in [5]. It was pointed out in [5] that cluster-extrema perform an evolution which “resembles” that of a Bessel bridge. Aïdekon et al. put this on rigorous ground, using a spine decomposition developed in [1], showing that the law of such paths is in fact that of a Brownian motion in a potential, see [2 , Theorem 2.4]. The clusters are then constructed by “attaching“ (according to a certain random mechanism) to each such path independent BBMs, and then passing to the limit \(t\rightarrow \infty \). Theorem 2.3 of [2] describes the resulting superposition of i.i.d. BBM’s. Although the method of proof is different from ours (in particular, [2] does not rely on the convergence results established by Bramson [17]), the ensuing description of the extremal process is compatible with our main theorem. An additional bridge between the two descriptions goes through the work of Chauvin and Rouault [21, 22] where a link between the spine decomposition and conditioned BBM is established, see Remark 3.5 below.
Very recently the ergodic properties at the edge of BBM have also been addressed. In [7], we proved a long-standing conjecture by Lalley and Sellke stating that the empirical (time-averaged) distribution function of the maximum of BBM converges almost surely to a double exponential, or Gumbel, distribution with a random shift. The method of proof relies again on the localization of the paths established in [5]. Furthermore, combining the methods developed in the present paper and those from [7], we obtained in [8] a similar type of ergodic theorem for the whole extremal process.
Despite the steady progress over the last years, a number of interesting questions concerning the properties of the extremal process of BBM are still left open. In particular, a more quantitative understanding of the law of the clusters and its self-similar structure would be desirable. As an example, the average density of particles of the extremal process has been conjectured by Brunet and Derrida to behave asymptotically as \((-x)e^{-\sqrt{2}x}\) for \(x\rightarrow -\infty \) [20]. This is the density of the intensity measure of the auxiliary process we introduce in this work, but the issues, although related, are not completely equivalent. As a matter of fact, none of the available descriptions of the extremal process and of the law of the clusters implies directly this result, though progress in this direction has been announced in [2].
Finally, we mention that Madaule [35] has recovered results on the extremal process of BBM for the discrete case of branching random walks.
3 The road to the Main Theorem
We first recall from [31] the standard setting for the study of point processes. Let \(\mathcal M \) be the space of Radon measures on \(\mathbb{R }\). Elements of \(\mathcal M \) are in correspondence with the positive linear functionals on \(\mathcal C _c(\mathbb{R })\), the space of continuous functions on \(\mathbb{R }\) with compact support. In particular, any element of \(\mathcal M \) is locally finite. The space \(\mathcal M \) is endowed with the vague topology, that is, \(\mu _n\rightarrow \mu \) in \(\mathcal M \) if and only if for any \(\phi \in \mathcal C _c(\mathbb{R })\), \(\int \phi \text{ d}\mu _n\rightarrow \int \phi \text{ d}\mu \). The law of a random element \(\Xi \) of \(\mathcal M \), or random measure, is determined by the collection of real random variables \(\int \phi \text{ d}\Xi \), \(\phi \in \mathcal C _c(\mathbb{R })\). A sequence \((\Xi _n)\) of random elements of \(\mathcal M \) is said to converge to \(\Xi \) if and only if for each \(\phi \in \mathcal C _c(\mathbb{R })\), the random variables \(\int \phi \text{ d}\Xi _n\) converges in the weak sense to \(\int \phi \text{ d}\Xi \). A point process is a random measure that is integer-valued almost surely. It is a standard fact that point processes are closed in the set of random elements of \(\mathcal M \), and that a sufficient condition for their convergence is the convergence of Laplace functionals.
3.1 The Laplace transform of the extremal process of BBM
Our first step towards Theorem 2.1 consists in showing that the extremal process \(\mathcal{E }_t\) is well defined in the limit of large times.
Theorem 3.1
(Existence of the limit) The point process \(\mathcal{E }_t =\sum _{k\le n(t)} \delta _{x_k(t) -m(t)}\) converges in law to a point process \(\mathcal{E }\).
Brunet and Derrida [20] have obtained a similar existence result for the extremal process \(\mathcal{E }_t\). To achieve this goal, they use the generating function that counts the number of the points to the right of fixed levels. Our method of proof is different, and relies on the convergence of Laplace functionals
for \(\phi \in \mathcal C _c(\mathbb{R })\) non-negative. It is easy to see that the Laplace functional is a solution of the F-KPP equation following the observation of McKean, see Lemma 4.1 below. However, convergence is more subtle. It will follow from the convergence theorem of Bramson, see Theorem 4.2 below, but only after an appropriate truncation of the functional needed to satisfy the hypotheses of the theorem. The proof recovers a representation of the form (1.8) and, more importantly, it provides an expression for the constant \(C\) as a function of the initial condition. This observation is inspired by the work of Chauvin and Rouault [21]. It will be at the heart of the representation theorem of the extremal process as a cluster process.
Proposition 3.2
Let \(\mathcal{E }_t\) be the process (1.10). For \(\phi \in \mathcal C _c(\mathbb{R })\) non-negative and any \(x\in \mathbb{R }\),
where, for \(v(t,y)\) solution of F-KPP (1.2) with initial condition \(v(0,y)=e^{-\phi (y)}\),
is a strictly positive constant depending on \(\phi \) only, and \(Z\) is the derivative martingale.
A straightforward consequence of Proposition 3.2 is the Invariance under superpositions of the random measure \(\mathcal{E }\), conjectured by Brunet and Derrida [19, 20].
Corollary 3.3
(Invariance under superposition) The law of the extremal process of the superposition of \(n\) independent BBM started at \(x_1, \dots , x_n \in \mathbb{R }\) coincides in the limit of large time with that of a single BBM, up to a random shift.
It is not hard to verify that a point process \(\Xi \) that is constructed from a Poisson point process with exponential density to which, at each atom, is attached an i.i.d. point process has the same law, up to a shift, as a superposition of \(n\) i.i.d. copies of \(\Xi \) for any \(n\in \mathbb{N }\). Brunet and Derrida conjectured that any point process whose law is invariant, up to shift, under a superposition of i.i.d. copies of itself must in fact be of this form. Maillard has proved this conjecture [36], but this general theorem provides no information on the law of the clusters.
Theorem 3.4
(The law of the clusters) Let \(x\equiv a\sqrt{t}+b\) for some \(a<0, b\in \mathbb{R }\). The point process
converges in law as \(t\rightarrow \infty \) to a well-defined point process \( \overline{\mathcal{E }}\). The limit does not depend on \(a\) and \(b\), and the maximum of \( \overline{\mathcal{E }}\) has the law of an exponential random variable.
The limiting process therefore inherits a “loss of memory” property from the large jump. This is the crucial point for the proof that the clusters are identically distributed.
Remark 3.5
BBMs conditioned on the atypical event \(\{\max _k x_k(t)-\sqrt{2}t >0\}\) in the limit of large times, such as the ones appearing in Theorem 3.4, have been studied by Chauvin and Rouault [21]. They show that the impact of the conditioning is twofold: first, on one path of the tree (and only one), the spine, the associated Brownian motion has a drift; second, the conditioning leads to an increase of both birth rate, and intensity. We refer the reader to [21, Theorem 3] for the precise statements.
3.2 An auxiliary point process
In this section, the method of proof of Theorem 2.1 using an auxiliary point process is explained. To make the distinction between the law of standard BBM, denoted by \(\mathbb{P }\), and the auxiliary construction, we introduce for convenience a new probability space. Let \((\Omega ^{\prime }, \mathcal F ^{\prime }, P)\) be a probability space, and \(Z: \Omega ^{\prime } \rightarrow \mathbb{R }_+\) with distribution as that of the limiting derivative martingale (1.7). Expectation with respect to \(P\) will be denoted by \(E\). On \((\Omega ^{\prime }, \mathcal F ^{\prime }, P)\), let \((\eta _i; i \in \mathbb{N })\) be the atoms of a Poisson point process \(\eta \) on \((-\infty ,0)\) with intensity measure
For each \(i\in \mathbb{N }\), consider independent BBMs on \((\Omega ^{\prime }, \mathcal F ^{\prime }, P)\) with drift \(-\sqrt{2}\), i.e. \(\{x_k^{(i)}(t) -\sqrt{2} t; k \le n^{(i)}(t)\}\), \(n^{(i)}(t)\) is the number of particles of the BBM \(i\) at time \(t\). Remark that, by 1.4 and 1.5, for each \(i\in \mathbb{N }\),
The auxiliary point process of interest is the superposition of the i.i.d. BBM’s with drift and shifted by \(\eta _i+\frac{1}{\sqrt{2}}\log Z\):
The existence and non-triviality of the process in the limit \(t\rightarrow \infty \) is not straightforward, especially in view of (3.6). It will be proved by recasting the problem into the frame of convergence of solutions of the F-KPP equations to travelling waves, as in the proof of Theorem 3.1.
It turns out that the density of the Poisson process points growing faster than exponentially as \(x\rightarrow -\infty \) compensates for the fact that BBM’s with drift wander off to \(-\infty \).
The connection between the extremal process of BBM and the auxiliary process is the following result:
Theorem 3.6
(The auxiliary point process) Let \(\mathcal{E }_t\) be the extremal process (1.10) of BBM. Then
The above will follow from the fact that the Laplace functionals of \(\lim _{t\rightarrow \infty }\Pi _t\) admits a representation of the form (3.2), and that the constants \(C(\phi )\) in fact correspond. An elementary consequence of the above identification is that the extremal process \(\mathcal E \) shifted back by \(\frac{1}{\sqrt{2}}\log Z\) is an infinitely divisible point process. The reader is referred to [31] for definitions and properties of such processes.
We conjectured Theorem (3.6) in a recent paper [6], where it is pointed out that such a representation is a natural consequence of the results on the genealogies and the paths of the extremal particles in [5]. The proof of Theorem 3.6 provided here does not rely on such techniques. It is based on the analysis of Bramson [17] and the subsequent works of Chauvin and Rouault [21, 22], and Lalley and Sellke [33]. However, the results on the genealogies of [5] provides a complementary intuition.
The approach to the problem in terms of the auxiliary point process is very close in spirit to the study of competing particle systems (CPS). These systems were introduced in the study of spin glasses [3, 4, 39], but are a good laboratory in general to study problems of extremal value statistics. The CPS approach can be seen as an attempt to formalize to so-called cavity method developed by Parisi and co-authors [38] for the study of spin glasses. The connection with Theorem 3.6 is as follows.
Let \(\mathcal{E } =\sum _{i\in \mathbb{N }}\delta _{e_i}\) be the limiting extremal process of a BBM starting at zero. It is clear since \(m(t) = m(t-s) + \sqrt{2} s + o(1)\) that the law of \(\mathcal{E }\) satisfies the following invariance property: for any \(s\ge 0\),
where \(\{x_k^{(i)}(s); k\le n^{(i)}(s)\}_{i\in \mathbb{N }}\) are i.i.d. BBM’s. On the other hand, by Theorem 3.6,
where now \((\eta _i; i\in \mathbb{N })\) are the atoms of a PPP\((\sqrt{\frac{2}{\pi }}(-x) \mathrm{e}^{-\sqrt{2}x}dx)\) on \((-\infty ,0]\) shifted by \(\frac{1}{\sqrt{2}} \log Z\).
The main idea of the CPS-approach is to characterize extremal processes as invariant measures under suitable, model-dependent stochastic mappings. In the case of BBM, the mapping consists of adding to each ancestor \(e_i\) independent BBMs with drift \(-\sqrt{2}\). This procedure randomly picks of the original ancestors only those with offspring in the lead at some future time. But the random thinning is performed through independent random variables: this suggests that one may indeed replace the process of ancestors \(\{e_i\}\) by a Poisson process with suitable intensity measure.
Behind the random thinning, a crucial phenomenon of “energy vs. entropy” is at work. Under the light of (3.6), the probability that any such BBM with drift \(-\sqrt{2}\) attached to the process of ancestors does not wander off to \(-\infty \) vanishes in the limit of large times. On the other hand, the higher the position of the ancestors, the fewer one finds. A delicate balance must therefore be met, and only ancestors lying on a precise level below the lead can survive the random thinning. This is the content of Proposition 3.8 below, and a fundamental ingredient in the CPS-heuristics: particles at the edge come from a precise location of the tail in the past. A key step in identifying the equilibrium measure is thus to identify the tail, or at least a good approximation of it. In the example of BBM, we are able to show, perhaps indirectly, that a good approximation of the tail is a Poisson process with intensity measure \((-x) \mathrm{e}^{-\sqrt{2}x}dx\) (up to constant) on \((-\infty ,0)\).
We now list some of the properties of the auxiliary process in the limit of large times, which by Theorem 3.6 coincide with those of the extremal process of BBM.
Proposition 3.7
(Poissonian statistics of the cluster-extrema) Consider \(\Pi _t^{\text{ ext}}\) the point process obtained by retaining from \(\Pi _t\) the maximal particles of the BBM’s,
Then \(\lim _{t\rightarrow \infty } \Pi _{t}^{\text{ ext}} \stackrel{\text{ law}}{=}PPP (Z \sqrt{2} C \mathrm{e}^{-\sqrt{2} x} \text{ d}x )\) as a point process on \(\mathbb{R }\), where \(C\) is the same constant appearing in (1.8). In particular, the maximum of \(\lim _{t\rightarrow \infty } \Pi _{t}^{\text{ ext}} \) has the same law as the limit law of the maximum of BBM.
The fact that the laws of the maximum of the cluster-extrema and of BBM correspond is a consequence of (1.8) and the formula for the maximum of a Poisson process. The presence of Poissonian statistics in the extremes of BBM was proved in [6] using the results on the genealogies in [5]. The proof given here is conceptually very different and based on the auxiliary process. The last ingredient for the proof of Theorem 2.1 is a very precise control on the location of the atoms \(\eta \) for which the particles of the associated BBM may reach the leading edge. The proposition is central to the proof of Theorem 3.4.
Proposition 3.8
Let \(y\in \mathbb{R }\) and \(\varepsilon >0\) be given. There exist \(0 < A_1 < A_2 < \infty \) and \(t_0\) depending only on \(y\) and \(\varepsilon \), such that
4 Proofs
In what follows, \(\{\,x_k(t),\, k\le n(t)\}\) will denote a branching Brownian motion on the interval of time \([0,t]\) with one particle at \(0\) at time \(0\). The law of BBM will be denoted by \(\mathbb{P }\) and its expectation by \(\mathbb{E }\). We recall that we will use \(P\) and \(E\) for the probability and the expectation of the auxiliary process to distinguish with the original process. We will consider the F-KPP equation (1.2) with general initial condition \(v(0,x)=f(x)\) for some function \(f\) that will depend on context. Initial condition (1.3) corresponds to \(f(x)=1_{\{-x\le 0\}}\). It will be often convenient to consider \(u(t,x)\equiv 1-v(t,x)\) instead of \(v(t,x)\). Note that \(u(t,x)\) is solution of the equation
with initial condition \(u(0,x)=1-f(x)\). We will refer to this equation as the F-KPP Eq. (4.1).
4.1 Estimates of solutions of the F-KPP equation
We start by stating two fundamental results that will be used extensively. First, McKean’s insightful observation:
Lemma 4.1
([37]) Let \(f: \mathbb{R }\rightarrow [0,1]\) and \(\{x_k(t): k\le n(t)\}\) a branching Brownian motion starting at \(0\). The function
is solution of the F-KPP Eq. (1.2) with initial condition \(v(0,x)= f(x)\).
The second fundamental result is the one of Bramson on the convergence of solutions of the F-KPP equation to travelling waves:
Theorem 4.2
(Theorem A, Theorem B and Example 2 in [17]) Let \(u\) be a solution of the F-KPP Eq. (4.1) with \(0\le u(0,x) \le 1\). Then
where \(\omega \) is the unique solution (up to translation) of
if and only if
-
1.
for some \(h>0\), \(\limsup _{t\rightarrow \infty } \frac{1}{t} \log \int _t^{t(1+h)} u(0,y) \text{ d}y \le -\sqrt{2}\);
-
2.
and for some \(\nu >0\), \(M>0\), \(N>0\), \(\int _{x}^{x+N} u(0,y) \text{ d}y > \nu \) for all \(x\le - M\).
Moreover, if \(\lim _{x\rightarrow \infty } \mathrm{e}^{b x}u(0,x) = 0\) for some \(b> \sqrt{2}\), then one may choose
It is to be noted that the necessary and sufficient conditions hold for uniform convergence in \(x\). Pointwise convergence could hold when, for example, condition 2 is not satisfied. This is the case in the proof of Theorem 3.1. The following Proposition provides sharp approximations to the solutions of the F-KPP equation.
Proposition 4.3
Let \(u\) be a solution to the F-KPP equation (4.1) with initial data satisfying the assumptions of Theorem 4.2 and
Define
Then for \(r\) large enough, \(t\ge 8r\), and \(X\ge 8r - \frac{3}{2\sqrt{2}}\log t\),
for some \(\gamma (r)\downarrow 1\) as \(r\rightarrow \infty \).
The function \(\psi \) thus fully captures the large space-time behavior of the solution to the F-KPP equations. We will make extensive use of (4.8), mostly when both \(X\) and \(t\) are large in the positive, in which case the dependence on \(X\) becomes particularly easy to handle.
Proof of Proposition 4.3
For \(T>0\) and \(0<\alpha < \beta <\infty \), let \(\{\mathfrak{z}_{\alpha , \beta }^T(s), 0\le s \le T\}\) denote a Brownian bridge of length \(T\) starting at \(\alpha \) and ending at \(\beta \).
It has been proved by Bramson (see [17, Proposition 8.3]) that for \(u\) satisfying the assumptions in the Proposition 4.3, the following holds:
-
(1)
for \(r\) large enough, \(t\ge 8r\) and \(x\ge m(t)+8r\)
$$\begin{aligned}&u(t,x)\ge K_1(r) e^{t-r}\int \limits _{-\infty }^\infty u(r,y) \frac{e^{-\frac{(x-y)^2}{2(t-r)}}}{\sqrt{2\pi (t-r)}}\mathbb{P }\,[\mathfrak z ^{t-r}_{x,y}(s)>\mathcal{\overline{M} }_{r,t}^x(t-s),\nonumber \\&\quad s\in [0,t-r]] \mathop {\text{ d}}\limits _{\cdot } y \end{aligned}$$and
$$\begin{aligned}&u(t,x)\le K_2(r) e^{t-r}\int \limits _{-\infty }^\infty u(r,y) \frac{e^{-\frac{(x-y)^2}{2(t-r)}}}{\sqrt{2\pi (t-r)}}\mathbb{P }[\mathfrak z ^{t-r}_{x,y}(s)>\underline{\mathcal{M }}_{r,t}^{\prime }(t-s),\nonumber \\&\quad s\in [0,t-r]]\text{ d}y \end{aligned}$$where the functions \(\overline{\mathcal{M }}_{r,t}^x(t-s)\), \(\underline{\mathcal{M }}_{r,t}^{\prime }(t-s)\) satisfy
$$\begin{aligned} \underline{\mathcal{M }}_{r,t}^{\prime }(t-s)\le n_{r,t}(t-s)\le \overline{\mathcal{M }}_{r,t}^x(t-s), \end{aligned}$$for \(s\mapsto n_{r,t}(s)\) being the linear interpolation between \(\sqrt{2}{r}\) at time \(r\) and \(m(t)\) at time \(t\). Moreover, \(K_1(r)\uparrow 1\), \(K_2(r)\downarrow 1\) as \(r\rightarrow \infty \).
-
(2)
If \(\psi _1(r,t,x)\) and \(\psi _2(r,t,x)\) denote respectively the lower and upper bound to \(u(t,x)\), we have
$$\begin{aligned} 1\le \frac{\psi _2(r,t,x)}{\psi _1(r,t,x)}\le \gamma (r) \end{aligned}$$where \(\gamma (r)\downarrow 1\) as \(r\rightarrow \infty \).
Hence, if we denote by
we have by domination \(\psi _1\le \widehat{\psi }\le \psi _2\). Therefore, for \(r,t\) and \(x\) large enough
and
Combining (4.10) and (4.11) we thus get
We now consider \(X \ge 8r - \frac{3}{2\sqrt{2}} \log t\), and obtain from (4.12) that
The probability involving the Brownian bridge in the definition of \(\widehat{\psi }\) can be explicitly computed. The probability of a Brownian bridge of length \(t\) to remain below the interpolation of \(A>0\) at time \(0\) and \(B>0\) at time \(t\) is \(1-e^{-2AB/t}\), see e.g. [40]. In the above setting the length is \(t-r\), \(A= x-m(t)=x -\sqrt{2}t+ \frac{3}{2\sqrt{2}}\log t>0\) for \(t\) large enough and \(B=y-\sqrt{2}r=y^{\prime }\). Using this, together with the fact that \(\mathbb{P }(\mathfrak z ^{t-r}_{x,y}(s)>n_{r,t}(t-s),s\in [0,t-r])\) is \(0\) for \(B=y^{\prime }<0\), and by change of variable \(y^{\prime }=y+\sqrt{2}t\) in the integral appearing in the definition of \(\widehat{\psi }\), we get
This, together with (4.12), concludes the proof of the proposition. \(\square \)
The bounds in (4.8) have been used by Chauvin and Rouault to compute the probability of deviations of the maximum of BBM, see Lemma 2 [21]. Their reasoning applies to solutions of the F-KPP equation with other initial conditions than those corresponding to the maximum. We give the statement below, and reproduce Chauvin and Rouault’s proof in a general setting for completeness.
Proposition 4.4
Let \(u\) be a solution to the F-KPP equation (4.1) with initial data satisfying the assumptions of Theorem 4.2 and
Then,
Moreover, the limit of the right-hand side exists as \(r\rightarrow \infty \), and it is positive and finite.
The Proposition will often be used with the initial condition \(u(0,x)={\small 1}\!\!1_{\{-x>\delta \}}\), \(\delta \in \mathbb{R }\).
Proof
Note that the condition (4.15) implies (). The first claim is straightforward from Proposition 4.3 if the limit \(t\rightarrow \infty \) can be taken inside the integral in the definition of \(\psi \). This is justified by dominated convergence. For \(t\) large enough, since \(e^{-x}\ge 1-x\) for \(x>0\), it is easy to check that \(\psi \) times \(e^{x\sqrt{2}}\frac{t^{3/2}}{\log t}\) is smaller than
It remains to show that (4.17) is integrable in \(y^{\prime } \ge 0\). To see this, let \(u^{(2)}(t,x)\) be the solution to \(\partial _t u^{(2)} = \frac{1}{2} u^{(2)}_{xx} - u^{(2)}\) (the linearised F-KPP-Equation (4.1) with initial conditions \(u^{(2)}(0,x) = u(0,x)\). By the maximum principle for nonlinear, parabolic p.d.e.’s, see e.g. [17, Corollary 1, p. 29],
Moreover, by the Feynman–Kac representation and the definition of \(y_0\),
and for any \(x>0\) we thus have the bound
Hence,
The upper bound is integrable over the desired measure since
Therefore dominated convergence can be applied and the first part of the proposition follows.
It remains to show that
Write \(C(r)\) for the integral. By Proposition 4.3, for \(r\) large enough,
and
Therefore since \(\gamma (r)\rightarrow 1\)
and
It follows that \(\lim _{r\rightarrow \infty } C(r)\equiv C\) exists and so does \(\lim _{t\rightarrow \infty }e^{x\sqrt{2}}\frac{t^{3/2}}{\frac{3}{2\sqrt{2}}\log t} u(t,x+\sqrt{2t})\). Moreover \(C>0\) otherwise
which is impossible since
for \(r\) large enough but finite. (\(\gamma (r)\) and \(C(r)\) are finite for \(r\) finite.) Moreover \(C<\infty \), otherwise
which is impossible since \(\lim _{t\rightarrow \infty }e^{x\sqrt{2}}\frac{t^{3/2}}{\frac{3}{2\sqrt{2}}\log t} u(t,x+\sqrt{2t})\le C(r)\gamma (r)\) for \(r\) large enough, but finite. \(\square \)
For the proof of Theorem 3.4, the following refinement of Proposition 4.4 is needed.
Lemma 4.5
Let \(u\) be a solution to the F-KPP equation (4.1) with initial data satisfying the assumptions of Theorem 4.2 and
Then, for \(x = a \sqrt{t}\), \(a>0\), and \(Y\in \mathbb{R }\),
where
Moreover, the convergence is uniform for \(a\) in a compact set.
Proof
The proof is a simple computation:
the last step by dominated convergence (cfr. (4.18)–(4.22). Using that \(x = a\sqrt{t}\),
hence
\(\square \)
The contribution to \(C=\lim _{r\rightarrow \infty }\sqrt{\frac{2}{\pi }} \int _0^\infty u(r,y+\sqrt{2}r) ~ ye^{y\sqrt{2}}\text{ d}y\) comes from the \(y\)’s of the order of \(\sqrt{r}\). This result will be used in the proof of Proposition 3.8.
Lemma 4.6
Let \(u\) be a solution to the F-KPP equation (4.1) with initial data satisfying the assumptions of Theorem 4.2 and
Then for any \(x\in \mathbb{R }\)
For the proof of the lemma, we use an estimate of the law of the maximum similar to the one of Proposition 4.3 that was used in [6].
Lemma 4.7
[6, Corollary 10] For \(X>1\), and \(t\ge t_o\) (for \(t_o\) a numerical constant),
for some constant \(\rho >0\).
,
Proof of Lemma 4.6
We prove the first limit. The proof of the second is identical. By assumption, \(u(0,y)\le {\small 1}\!\!1_{\{y<y_0+1\}}\). It follows from Lemma 4.1 that
It thus suffices to prove the result for the right side. Write for simplicity \(\delta =x+y_0+1\).
We have by the change of variable \(y\rightarrow y+\delta +\frac{3}{2\sqrt{2}} \log r\)
By Lemma 4.7, the first term of () is smaller than
By the change of variable \(y\rightarrow \frac{y}{\sqrt{r}}\), this becomes
As \(r \rightarrow \infty \), this integral is bounded by a Gaussian integral which goes to zero as \(A_1\downarrow 0\). The second term in 4.33 is bounded similarly. The resulting integral is the one of 4.34 with \(y/\sqrt{r}\) instead of \(y^2\) in the integrand. Therefore, it goes to zero as \(r\rightarrow \infty \). This establishes (4.30). \(\square \)
The following lemma tells us how \(C=\lim _{r\rightarrow \infty }\sqrt{\frac{2}{\pi }}\int _0^\infty u(r,y+\sqrt{2}r) ~ye^{y\sqrt{2}}\text{ d}y\) behaves when \(u\) is shifted.
Lemma 4.8
Let \(u\) be a solution to the F-KPP equation (4.1) with initial data satisfying the assumptions of Theorem 4.2 and
Let
whose existence is ensured by Proposition 4.4. Then for any \(x\in \mathbb{R }\):
Proof
The claim will follow by Proposition 4.4, if it is shown that
Note that the limit on the right-hand side exists by the proposition.
The definition of \(\psi \) in (4.7) and the change of variable \(y^{\prime }=y+x\) gives
From this, a dominated convergence argument identical to the one in the proof of Proposition 4.4 implies
In the limit \(r\rightarrow \infty \), the contribution for any finite interval is zero because \(u(r,x+y+\sqrt{2}r)\rightarrow 0\) as \(r\rightarrow \infty \). Therefore the integral can be replaced by \(\int _0^\infty \). To establish 4.38, it remains to prove that
This is done exactly as in Lemma 4.6. In (), take \(A_1=\infty \) and replace \(y^2\) by \(y\). Following the same estimate gives a Gaussian integral in () with \(y/\sqrt{r}\) instead of \(y^2\). Hence, the integral goes to zero as \(r\rightarrow \infty \). \(\square \)
4.2 Existence of a limiting process
Proof of Theorem 3.1
It suffices to show that, for \(\phi \in \mathcal C _c(\mathbb{R })\) positive, the Laplace transform \(\Psi _t(\phi )\), defined in (3.1), of the extremal process of BBM converges. Remark first that this limit cannot be \(0\), since in the case of BBM it can be checked as in [5] that
hence the limiting point process must be locally finite.
For convenience, we define \(\max \mathcal E _t \equiv \max _{k\le n(t)} x_k(t)-m(t)\). By Theorem 4.2 applied to the function
it holds that
Now consider for \(\delta >0\)
Note that by (4.43), the second term on the r.h.s of 4.44 satisfies
It remains to address the first term on the r.h.s of (4.44). Write for convenience
We claim that the limit
exists, and is strictly smaller than one. To see this, set \(g_\delta (x) \equiv \mathrm{e}^{-\phi (x)} {\small 1}\!\!1_{\{x \le \delta \}}\), and
By Lemma 4.1, \(u_\delta \) is then solution to the F-KPP equation 1.2 with \(u_\delta (0,x)= g_\delta (-x)\). Moreover, \(g_\delta (-x)= 1\) for \(x\) large enough in the positive, and \(g_\delta (-x)=0\) for \(x\) large enough in the negative, so that conditions \((1)\) and \((2)\) of Theorem 4.2 are satisfied as well as (4.5) on the form of \(m(t)\). Note that this would not be the case without the presence of the cutoff. Therefore
converges as \(t\rightarrow \infty \) uniformly in \(x\) by Theorem 4.2. But
and therefore the limit \(\lim _{t\rightarrow \infty } \Psi _t^\delta (\phi ) \equiv \Psi ^\delta (\phi )\) exists. But the function \(\delta \mapsto \Psi ^\delta (\phi )\) is increasing and bounded by construction. Therefore, \(\lim _{\delta \rightarrow \infty } \Psi ^\delta (\phi ) = \Psi (\phi )\) exists. Moreover, there is the obvious bound
since the maximum is an atom of \(\mathcal E _t\) and \(\phi \) is non-negative. The limit \(t\rightarrow \infty \) and \(\delta \rightarrow \infty \) of the right side exists and is strictly smaller than \(1\) by the convergence in law of the re-centered maximum to \(\omega (x)\) (note that the support of \(\omega (x)\) is \(\mathbb{R }\)). Therefore \(\Psi (\phi ) =\lim _{\delta \rightarrow \infty }\lim _{t\rightarrow \infty }\Psi _t^\delta (\phi )<1\) which proves (4.46). \(\square \)
4.3 The Laplace functional and the F-KPP equation
Proof of Proposition 3.2
The proof of the proposition will be broken into proving two lemmas.
In the first lemma we establish an integral representation for the Laplace functionals of the extremal process of BBM which are truncated by a certain cutoff; in the second lemma we show that the results continues to hold when the cutoff is lifted. Throughout this section, \(\phi :\mathbb{R }\rightarrow [0,\infty )\) is a non-negative continuous function with compact support.
Lemma 4.9
Consider
Then \(u_\delta (t,x)\) is the solution of the F-KPP equation (4.1) with initial condition \(u_\delta (0,x)=1-e^{-\phi (-x)}1(-x\le \delta )\). Moreover, the following limit exists
and
Proof
The first part of the Lemma is proved in the proof of Theorem 3.1, whereas (4.50) follows from Theorem 4.2 and the representation (1.8). It remains to prove (4.49). The proof is a refinement of Proposition 4.4 that recovers the asymptotics (1.9).
For \(u_\delta \) as above, let \(\psi (r,t,x)\) be its approximation as in Proposition 4.3 and choose \(x, r\) so that \(x\ge m(t)+8r\). By Proposition 4.3 we then have the bounds
where
Using dominated convergence as in Proposition 4.4, one gets
Putting this back in (4.51),
for \( C(r) \equiv \sqrt{\frac{2}{\pi }}\int _0^\infty u_\delta (r,y^{\prime }+\sqrt{2}r)y^{\prime }e^{y^{\prime }\sqrt{2}} \text{ d}y^{\prime }, \) and \(x> 8r\). We know that \(\lim _{r\rightarrow \infty } C(r) \equiv C>0\) exists by Proposition 4.4. Thus taking \(x=9r\), letting \(r\rightarrow \infty \) in (4.52), and using that \(\gamma (r)\downarrow 1\), one has
On the other hand, the representation (1.8) and the asymptotics (1.9) yield
The claim follows from the last two equations.\(\square \)
The results of Lemma 4.9 also hold when the cutoff is removed. Essentially, one needs to prove that the limit \(t\rightarrow \infty \) and \(\delta \rightarrow \infty \) can be interchanged. The proof shows (non-uniform) convergence of the solution of the F-KPP equation when one condition of Theorem 4.2 is not fulfilled. With an appropriate continuity argument, a Lalley-Sellke type representation is also recovered.
Lemma 4.10
Let \(u(t,x), u_\delta (t, x)\) be solutions of the F-KPP equation (4.1) with initial condition \(u(0,x)=1-e^{-\phi (-x)}\) and \(u_\delta (0, x)= 1-e^{-\phi (-x)}{\small 1}\!\!1_{\{-x\le \delta \}}\), respectively. Set \(C(\delta , \phi ) \equiv \lim _{t\rightarrow \infty } \sqrt{\frac{2}{\pi }}\int _0^{\infty } u_\delta (t,y+\sqrt{2}t)ye^{\sqrt{2}y} \text{ d}y\). Then \(\lim _{\delta \rightarrow \infty } C(\phi ,\delta )\) exists, and
Moreover
Proof
Since \(\phi \) is non-negative, it is easy to see from Lemma 4.1 that
from which it follows that
Define
and
The inequalities in (4.58) then read
By Lemma 4.8, it holds
Remark also that Proposition 4.4 implies that for each \(\delta \), \(\lim _{t \rightarrow \infty } F(t, \delta ) \equiv F(\delta )\) exists and is strictly positive. We thus deduce from (4.62) that
We claim that \(\lim _{\delta \rightarrow \infty } F(\delta )\) exists, is strictly positive and finite. To see this, we first observe that the function \(\delta \rightarrow F(\delta )\) is by construction decreasing, and positive, therefore the limit \(\lim _{\delta \rightarrow \infty } F(\delta )\) exists. Strict positivity is proved in a somewhat indirect fashion: we proceed by contradiction, and rely on the convergence of the process of cluster extrema. Assume that
and thus that
Using the form of the Laplace functional of a Poisson process, we have that
Therefore, (4.66) would imply that
This cannot hold. In fact, for \(\Pi _t^{\text{ ext}}\) the process of the cluster-extrema defined earlier, one has the obvious bound
Since the process of cluster-extrema converges, by Proposition 3.7, to a PPP \(( C Z~ \sqrt{2} \mathrm{e}^{-\sqrt{2}x} \text{ d}x)\),
This contradicts (4.68) and therefore also (4.66). \(\square \)
Proposition 3.2 now follows directly from Lemma 4.10. \(\square \)
Proof of Corollary 3.3
Consider \(n\) independent copies \(\mathcal E ^{(i)}\), \(i=1,\dots ,n\) of \(\mathcal E \). By independence and by Proposition , the Laplace functional for \(\phi \in \mathcal C _c(\mathbb{R })\) of the superposition of these is
where \(Z^{(i)}\), \(i=1,\dots ,n\) are i.i.d. copies of the derivative martingale. The log of the variable \(\sum _{i=1}^nZ^{(i)}\) acts simply as a random shift in \(x\). Therefore \(\sum _{i=1}^n\mathcal E ^{(i)}_t\) has the same law as \(\mathcal E \) shifted by log of \(Z\). \(\square \)
4.4 The auxiliary process
Recall from Sect. 3.2 that \((\Omega ^{\prime },\mathcal{F }^{\prime },P)\) stands for the probability space on which the auxiliary point process \(\Pi _t\) is defined. The expectation under \(P\) is denoted by \(E\).
4.4.1 The process of cluster-extrema
In this section, we prove Proposition 3.7 on the convergence of the process of the cluster-extrema to a PPP\(( C Z \sqrt{2}\mathrm{e}^{-\sqrt{2}x} \text{ d}x )\). We remark that the proof is independent of Lemma 4.10 which uses the result.
A consequence of Lemma 4.8 is the following vague convergence of the maximum when integrated over the appropriate density.
Lemma 4.11
Let \(b\in \mathbb{R }\) and \(h(x)={\small 1}\!\!1_{[b,\infty )}(x)\). Then
Moreover, the convergence also holds for a continuous function \(h(x)\) that is bounded and is zero for \(x\) small enough:
Proof
The first assertion is direct from Lemma 4.8 with initial condition \(u(0,x)={\small 1}\!\!1_{\{x<0\}}\). For the second claim, note that the statement holds for any linear combination of functions of the form \({\small 1}\!\!1_{[b,\infty )}(x)\). Suppose for simplicity that \(|h(x)|\le 1\). By assumption, it is possible to find \(\delta >0\) such that \(h(x)=0\) for \(x<-\delta \). Moreover, for any \(\varepsilon >0\), \(\delta \) can be taken large enough so that \(Ce^{-\sqrt{2}\delta }<\varepsilon \). On \([-\delta ,\delta ]\), \(h\) can be approximated uniformly by linear combinations of indicator functions of the form \({\small 1}\!\!1_{[b,\infty )}(x)\). Therefore, (4.72) holds for \(h\) restricted to this interval. On \((\delta ,\infty )\), the term
is smaller than \(\varepsilon \) by the choice of \(\delta \) and the bound \(|h(x)|\le 1\). Since \(\varepsilon \) is arbitrary, the conclusion holds. \(\square \)
Proof of Proposition 3.7
Consider
where \(\eta =(\eta _i)\) is a Poisson process on \((-\infty ,0)\) with intensity measure \(\sqrt{\frac{2}{\pi }}(-y)e^{-\sqrt{2}y}dy\), and \(M^{(i)}(t)\equiv \max _k x_k^{(i)}(t)\). We show that
Since the underlying process is Poisson and the \(M^{(i)}\)’s are i.i.d. ,
where \(M(t)\) has the same distribution as one copy of the variables \(M^{(i)}(t)\). The result then follows from Lemma with \(h(x)=1-e^{-\phi (x)}\) after taking the limit.\(\square \)
4.4.2 Identification with the extremal process
Proposition 4.10 yields a short proof of Theorem .
Proof of Theorem 3.6
The Laplace functional of \(\Pi _t\) using the form of the Laplace functional of a Poisson process reads
with
By (4.37),
and the limit exists and is strictly positive by Lemma 4.10. This implies that the Laplace functionals of \(\lim _{t\rightarrow \infty }\Pi _t\) and of the extremal process of BBM are equal. \(\square \)
4.4.3 Properties of the clusters
In this section we prove Proposition 3.8 and Theorem 3.4.
Proof of Proposition 3.8
Throughout the proof, the probabilities are considered conditional on \(Z\). We show that for \(\varepsilon >0\) there exist \(A_1, A_2\) such that
We claim that, for \(t\) large enough, there exists \(A_1>0\) small enough such that
and \(A_2>0\) large enough such that
By Markov’s inequality and the fact that \(\sqrt{\frac{2}{\pi }}<1\), the left-hand side of (4.77) is less than
This can be smaller than \(\varepsilon /2\) by Lemma 4.6 by taking \(A_1\) small enough. The same reasoning can be applied to (4.78) thereby establishing the proposition. \(\square \)
Proof of Theorem 3.4
Let \((x_i(t), i\le n(t))\) be a standard BBM of law \(\mathbb{P }\). Let \(a\in I\), a compact interval in \((-\infty ,0)\) and \(b\in \mathbb{R }\). Set \(x=a\sqrt{t}+b\). Consider
and \(\max \overline{\mathcal{E }}_t\equiv \max _i x_i(t)-\sqrt{2}t\). We first claim that \( x + \max \overline{\mathcal{E }}_t\) conditionally on \(\{ x + \max \overline{\mathcal{E }}_t >0\}\) converges weakly to an exponential random variable,
for \(X>0\) and \(0\) otherwise. Remark, in particular, that the limit does not depend on \(x\).
To see (4.81), we write the conditional probability as
For \(t\) large enough (and hence \(-x\) large enough in the positive) we may apply the uniform bounds from Proposition 4.3 in the form
and
where \(\psi \) is as in (4.7) and the \(u\) entering into its definition is solution to F-KPP with Heaviside initial conditions, and \(r\) is large enough. Therefore,
By Lemma 4.5,
Taking the limit \(t\rightarrow \infty \) first, and then \(r\rightarrow \infty \) (and using that \(\gamma (r) \downarrow 1\)) we thus see that (4.85) implies (4.81).
Second, we show that for any function \(\phi \) that is continuous with compact support, the limit of
exists and is independent of \(x\). It follows from the first part of the proof that the conditional process has a maximum almost surely. It is thus sufficient to consider the truncated Laplace functional, that is for \(\delta >0\),
The above conditional expectation can be written as
Define
so that
Remark that the functions \(u_1, u_2\) and \(u_3\), all solve the F-KPP equation 4.1 with initial conditions
They also satisfy the assumptions of Theorem 4.2 and Proposition 4.3.
Let \(\psi _i\) be as in (4.7) with \(u\) replaced by the appropriate \(u_i\), \(i=1,2,3\). By Proposition 4.3,
By Lemma 4.5, the above limits exist and do not depend on \(x\). This shows the existence of (4.88). It remains to prove that this limit is non-zero for a non-trivial \(\phi \), thereby showing the existence and local finiteness of the conditional point process. To see this, note that, by Proposition 4.4, the limit of (4.88) equals
where \(C_i=\lim _{t\rightarrow \infty }\int _{-\infty }^0 u_i(t,y^{\prime }+\sqrt{2}t)(-y^{\prime })e^{-\sqrt{2}y^{\prime }} \text{ d}y^{\prime }\) for \(u_i\) as above. Note that \(0<C_3<\infty \), since by the representation of Proposition 3.2
and this probability is non-trivial. Now suppose \(C_1=C_2\). Then by Theorem 3.1 again, this would entail
where \(\mathcal E _t=\sum _i \delta _{x_i(t)-m(t)}\) and \(\max \mathcal E _t=\max _i x_i(t)-m(t)\). Thus,
But this is impossible since the maximum has positive probability of occurrence in \([0,\delta ]\) for any \(\delta \) and the process \(\lim _{t\rightarrow \infty }\mathcal E _t\) is locally finite. This concludes the proof of the Proposition. \(\square \)
Define the gap process at time \(t\)
Let us write \(\overline{\mathcal{E }}\) for the point process obtained in Theorem 3.4 from the limit of the conditional law of \(\overline{\mathcal{E }}_t\) given \(\max \overline{\mathcal{E }}_t>0\). We denote by \(\max \overline{\mathcal{E }}\) the maximum of \(\overline{\mathcal{E }}\), and by \(\mathcal D \) the process of the gaps of \(\overline{\mathcal{E }}\), that is the process \(\overline{\mathcal{E }}\) shifted back by \(\max \overline{\mathcal{E }}\). The following corollary is the fundamental result showing that \(\mathcal D \) is the limit of the conditioned process \(\mathcal D _t\), and, perhaps surprisingly, the process of the gaps in the limit is independent of the location of the maximum.
Corollary 4.12
Let \(x=a\sqrt{t}\), \(a<0\). In the limit \(t\rightarrow \infty \), the random variables \(\mathcal D _t\) and \(x+\max \overline{\mathcal{E }}\) are conditionally independent on the event \(x+\max \overline{\mathcal{E }}>b\) for any \(b\in \mathbb{R }\). More precisely, for any bounded continuous function \(f,h\) and \(\phi \in \mathcal C _c(\mathbb{R })\),
Moreover, convergence is uniform in \(x=a\sqrt{t}\) for \(a\) in a compact set.
Proof
By standard approximation, it suffices to establish the result for \(h(y)={\small 1}\!\!1_{\{y>b^{\prime }\}}\) for \(b^{\prime }>b\). By the property of conditioning and since \(b^{\prime }>b\)
The conclusion will follow from Theorem 3.4 by taking the limit \(t\rightarrow \infty \), once it is shown that convergence of \((\overline{\mathcal{E }}_t, y+ \max \overline{\mathcal{E }}_t)\) under the conditional law implies convergence of the gap process \(\mathcal D _t\). This is a general continuity result which is done in the next lemma. \(\square \)
Lemma 4.13
Let \((\mu _t,X_t)\) be a sequence of random variables on \((\mathcal M \times \mathbb{R }, \mathbb{P })\) that converges to \((\mu ,X)\) in the sense that for any bounded continuous function \(f,h\) on \(\mathbb{R }\) and any \(\phi \in \mathcal C _c(\mathbb{R })\)
Then for any \(\phi \in \mathcal C _c(\mathbb{R })\) and \(g:\mathbb{R }\rightarrow \mathbb{R }\), bounded continuous,
Proof
Let \(\varepsilon >0\) and \(f:\mathbb{R }\rightarrow \mathbb{R }\) be a bounded continuous function. Introduce the notation
We need to show that for \(t\) large enough
By standard approximations, it is enough to suppose \(f\) is Lipschitz, whose constant we assume to be \(1\) for simplicity.
Since the random variables \((X_t)\) are tight by assumption, there exists a compact interval \(K_\varepsilon \) of \(\mathbb{R }\) such that for \(t\) large enough
Now divide \(K_\varepsilon \) into \(N\) intervals \(I_j\) of equal length. Write \(\bar{x}_j\) for the midpoint of \(I_j\). For each of these intervals, one has
for
Since \(f\) is Lipschitz, the right-hand side is smaller than
Moreover
Note that there exists a compact \(C\), independently of \(t\) and \(j\) so that \(|\phi (y+X_t)-\phi (y+\bar{x}_j)|=0\) for \(y\notin C\) (it suffices to take \(C\) so that it contains all the translates \(\text{ supp} ~\phi +k\), \(k\in K_\varepsilon \)). By taking \(N\) large enough, \(|y+X_t- (y+\bar{x}_j)|=|\bar{x}_j-X_t|<\delta _\phi \) for the appropriate \(\delta _\phi \) making \(|\phi (y+X_t)-\phi (y+\bar{x}_j)|<\varepsilon \), uniformly on \(y\in C\). Hence, 4.102 is smaller than
The summation over \(j\) is thus smaller than \(\varepsilon \mathbb{E }[\mu _t(C)]\). By the convergence of \((\mu _t)\), this can be made smaller for \(t\) large enough.
The same approximation scheme for \((\mu ,X)\) yields
where \(\sum _j \mathcal R (j)\le \varepsilon \mathbb{E }[\mu (C)]\). Therefore (4.99) will hold provided that the difference of the first terms of the right-hand side of (4.101) and of (4.103) is small for \(t\) large enough and \(N\) fixed. But this is guaranteed by the hypotheses on the convergence of \((\mu _t,X_t)\). \(\square \)
4.5 Characterisation of the extremal process
Proof of Theorem 2.1
It suffices to show that for \(\phi : \mathbb{R }\rightarrow \mathbb{R }_+\) continuous with compact support, the Laplace functional \(\Psi _t(\phi )\) of the extremal process \(\mathcal E _t\) of BBM satisfies
for the point process \(\mathcal D \) of Corollary 4.12.
Now, by Theorem 3.6,
Using the form for the Laplace transform of a Poisson process we have for the right side
Let \(\mathcal D _t\) as in (4.94). The integral on the right-hand side above can be written as
for the bounded (on \([0,\infty )\)) continuous function \(f(x)=1-e^{-x}\), and where \(T_x\phi (y)=\phi (y+x)\). Note that \(f(0)=0\). By Proposition 3.8, there exist \(A_1\) and \(A_2\) such that
where the error term satisfies \(\lim _{A_1\downarrow 0, A_2 \uparrow \infty } \sup _{t\ge t_0}\, \Omega _t(A_1, A_2) = 0.\) Let \(m_\phi \) be the minimum of the support of \(\phi \). Note that
is zero when \(y+\max \overline{\mathcal{E }}_t< m_\phi \), and that the event \(\{y+\max \overline{\mathcal{E }}_t=m_\phi \}\) has probability zero. Therefore,
By Corollary 4.12, the conditional law of the pair \((\mathcal D _t, y+\max \overline{\mathcal{E }}_t)\) given \(\{y+\max \overline{\mathcal{E }}_t> m_\phi \}\) exists in the limit. Moreover the convergence is uniform in \(y \in [-A_1 \sqrt{t}, -A_2 \sqrt{t}]\). By Lemma 4.13, the convergence applies to the random variable \(\int \left\{ T_{y+\max \overline{\mathcal{E }}_t}\phi (z)\right\} \mathcal D _t(\text{ d}z)\). Therefore
On the other hand,
by Lemma 4.11 and by the same approximation as in (4.107).
Combining (4.110), (4.109) and () gives that (4.106) converges to
which is by (4.105) also the limiting Laplace transform of the extremal process of BBM: this shows (4.104) and thus concludes the proof of Theorem 2.1. \(\square \)
References
Aïdekon, É.: Convergence in law of the minimum of a branching random walk. Ann. Probab. arXiv:1101.1810 (to appear)
Aïdekon, É., Berestycki, J., Brunet, É., Shi, Z.: The Branching Brownian motion seen from its tip. arXiv:11.04.3738v3
Aizenman, M., Arguin, L.-P.: On the structure of quasi-stationary competing particle systems. Ann. Probab. 37, 1080–1113 (2009)
Aizenman, M., Sims, R., Starr, S.: Mean field spin glass models from the cavity-ROSt perspective. In: Prospects in Mathematical Physics, Contemporary Mathematics, vol. 437, pp. 1–30. American Mathematical Society, Providence (2007)
Arguin, L.-P., Bovier, A., Kistler, N.: The genealogy of extremal particles in Branching Brownian motion. Comm. Pure Appl. Math. 64, 1647–1676 (2011)
Arguin, L.-P., Bovier, A., Kistler, N.: Poissonian statistics in the extremal process of branching Brownian motion. Annals Appl. Probab. 22, 1693–1711 (2012)
Arguin, L.-P., Bovier, A., Kistler, N.: An ergodic theorem for the frontier of branching Brownian motion. arXiv:1201.1701 (2012)
Arguin, L.-P., Bovier, A., Kistler, N.: An ergodic theorem for the extremal process of branching Brownian motion. arXiv:1209.6027 (2012)
Aronson, D.G., Weinberger, H.F.: Nonlinear diffusion in population genetics, combustion and nerve propagation. In: Goldstein, J.A. (ed.) Partial Differential Equations and Related Topics Lecture Notes in Mathematics, vol. 446, pp. 5–49. Springer, New York (1975)
Aronson, D.G., Weinberger, H.F.: Multi-dimensional nonlinear diffusions arising in population genetics. Adv. Math. 30, 33–76 (1978)
Bolthausen, E., Deuschel, J.-D., Giacomin, G.: Entropic repulsion and the maximum of the two-dimensional Harmonic crystal. Ann. Probab. 29, 1670–1692 (2001)
Bolthausen, E., Deuschel, J.-D., Zeitouni, O.: Recursions and tightness for the maximum of the discrete, two-dimensional Gaussian free field. Electron. Commun. Probab. 16, 114–119 (2011)
Bovier, A.: Statistical mechanics of disordered systems. A mathematical perspective. Cambridge Universtity Press, Cambridge (2005)
Bovier, A., Kurkova, I.: Derrida’s generalized random energy models. 1. Models with finitely many hierarchies. Ann. Inst. H. Poincare. Prob. et Statistiques (B) Prob. Stat. 40, 439–480 (2004)
Bovier, A., Kurkova, I.: Kurkova Derrida’s generalized random energy models. 2. Models with continuous hierarchies. Ann. Inst. H. Poincare. Prob. et Statistiques (B) Prob. Stat. 40, 481–495 (2004)
Bramson, M.: Maximal displacement of branching Brownian motion. CPAM 31, 531–581 (1978)
Bramson, M.: Convergence of solutions of the Kolmogorov equation to travelling maves. Mem. Am. Math. Soc. 44(285), iv+190 pp (1983)
Bramson, M., Zeitouni, O.: Tightness of the recentered maximum of the two-dimensional discrete Gaussian free field. Comm. Pure Appl. Math. 65(1), 1–20 (2012)
Brunet, E., Derrida, B.: Statistics at the tip of a Branching random walk and the delay of traveling waves. Europhys. Lett. 87, 60010 (2009)
Brunet, E., Derrida, B.: A branching random walk seen from the tip. J. Statist. Phys. 143, 420–446 (2011)
Chauvin, B., Rouault, A.: Supercritical branching Brownian motion and KPP equation in the critical speed-area. Math. Nachr. 149, 299–314 (1990)
Chauvin, B., Rouault, A.: KPP equation and supercritical branching Brownian motion in the subcritical speed area. Application to spatial trees. Prob. Theor. Rel. Fields 80, 299–314 (1988)
Dembo, A.: Simple random covering. disconnection, late and favorite points. In: Proceedings of the International Congress of Mathematicians, Madrid III, pp. 535–558 (2006)
Dembo, A., Peres, Y., Rosen, J., Zeitouni, O.: Cover times for Brownian motion and random walks in two dimensions. Ann. Math. 160, 433–464 (2004)
Derrida, B.: A generalization of the random energy model that includes correlations between the energies. J. Phys. Lett. 46, 401–407 (1985)
Derrida, B., Spohn, H.: Polymers on disordered trees, spin glasses, and travelling waves. J. Statist. Phys. 51, 817–840 (1988)
Ding, J., Zeitouni, O.: Extreme values for two-dimensional discrete Gaussian free field. arXiv: 1206.0346 (2012)
Duplantier, B., Rhodes, R., Sheffield, S., Vargas, V.: Critical Gaussian multiplicative chaos: convergence of the derivative Martingale. arXiv: 1206.1671 (2012)
Fisher, R.A.: The wave of advance of advantageous genes. Ann. Eugen. 7, 355–369 (1937)
Harris, S.C.: Travelling-waves for the FKPP equation via probabilistic arguments. Proc. Roy. Soc. Edin. 129A, 503–517 (1999)
Kallenberg, O.: Random Measures. Springer, Berlin (1983)
Kolmogorov, A., Petrovsky, I., Piscounov, N.: Etude de l’ Équation de la diffusion avec croissance de la Quantité de Matière et son application à un problème Biologique, Moscou Universitet. Bull. Math. 1, 1–25 (1937)
Lalley, S.P., Sellke, T.: A conditional limit theorem for the frontier of a branching Brownian motion. Ann. Probab. 15, 1052–1061 (1987)
Leadbetter, M.R., Lindgren, G., Rootzen, H.: Extremes and related properties of random sequences and processes. Springer Series in Statistics. Springer, New York/Berlin (1983)
Madaule, T.: Convergence in law for the branching random walk seen from its tip. arXiv:1107.2543
Maillard, P.: A characterisation of superposable random measures, arXiv:1102.1888.
McKean, H.P.: Application of Brownian motion to the equation of Kolmogorov–Petrovskii–Piskunov. Comm. Pure Appl. Math. 28, 323–331 (1976)
Mézard, M., Parisi, G., Virasoro, M.: Spin Glass Theory and Beyond. World scientific, Singapore (1987)
Ruzmaikina, A., Aizenman, M.: Characterization of invariant measures at the leading edge for competing particle systems. Ann. Probab. 33, 82–113 (2005)
Scheike, T.H.: A boundary-crossing result for Brownian motion. J. Appl. Probab. 29, 448–453 (1992)
Talagrand, M.: Spin Glasses: A Challenge for Mathematicians. Cavity and Mean Field Models. Springer, Berlin (2003)
Author information
Authors and Affiliations
Corresponding author
Additional information
L.-P. Arguin was supported by the NSF grant DMS-0604869 during this work. L.-P. Arguin also acknowledges support from NSERC Canada and FQRNT Québec. A. Bovier is partially supported through the German Research Council in the SFB 611 and the Hausdorff Center for Mathematics. N. Kistler is partially supported by the Hausdorff Center for Mathematics. Part of this work has been carried out during the Junior Trimester Program Stochastics at the Hausdorff Center in Bonn, and during a visit by the third named author to the Courant Institute at NYU: hospitality and financial support of both institutions are gratefully acknowledged.
Rights and permissions
About this article
Cite this article
Arguin, LP., Bovier, A. & Kistler, N. The extremal process of branching Brownian motion. Probab. Theory Relat. Fields 157, 535–574 (2013). https://doi.org/10.1007/s00440-012-0464-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00440-012-0464-x