1 Introduction

Our main concern is the prediction of the deformation of a solid body under dynamic loads. It is possible to treat this as a transport problem, which in itself is of great interest for many fields of science and engineering. Consequently, a number of different numerical tools exist for finding solutions. A rough classification puts them into two groups, either working at a macroscopic or at a microscopic scale. The macroscopic methods, like the finite element method (FEM), the finite difference method (FDM), or the finite volume method (FVM), reduce the governing differential equations to algebraic equations by means of discretization. On the other hand, microscopic methods, such as molecular dynamics (MD) or direct Monte Carlo simulations (DMCS), strive to track the interactions of individual particles, which is rather computationally intensive. A different approach is undertaken in statistical mechanics by describing systems with large particle numbers probabilistically. This approach is utilized in a lattice Boltzmann method (LBM), which can be seen as a method associated with the mesoscopic scale. It is based on Boltzmann’s transport equation, which describes transport via the time evolution of an associated distribution function in phase space. The microscopic theory of the model is incorporated on an atomistic level through particle collisions. The LBM arises from the Boltzmann equation by discretizing the underlying phase space. The spatial domain is approximated by a lattice, in which the discrete points, or sites, are linked to each other. The velocity domain is reduced to a set of discrete lattice velocities, facilitating exchange between the sites. Thus, solving transport problems is broken down into two steps: on-site collisions and subsequent transport of the distribution functions, modeled as streaming along the links.

Since its beginnings in the 1980s, the LBM has been widely applied in the field of computational fluid dynamics, with a range of different techniques, such as single and multiphase flows or single and multi-relaxation time methods, see, e.g., [1,2,3,4]. Additionally, the method has been adapted for different physical models beyond fluids, such as wave propagation [5,6,7] and elastic waves [8,9,10,11] in different media. But the range of applications of the LBM has also been expanded to the simulation of elastic solids [12,13,14,15], although not much work has been published in this field yet. Only a few researchers work on the basics and an extensive method is still to be developed.

The application of such a LBM in fracture mechanics [16] has already been proposed. In our previous work [17] we used the wave model of Yan [5] to solve a reduced mechanical problem and examined a stationary crack under load. The present work builds thereon and presents two methods of non-lattice-conforming boundary conditions. With these, the boundaries of the physical domain do not need to adhere to boundaries of the lattice representation. This allows for more complex geometries to be regarded, such as circular holes within a domain. Additionally, cracks were modeled as notches of finite width in [17], whereas they can be correctly regarded as cuts of zero thickness within the probe with the new approaches. Until now, boundary conditions have not been a focus for a LBM in solid mechanics.

Section 2 describes the simplified elastodynamic problem that is considered in the present work, namely the mechanics of antiplane shear deformation of a homogeneous linear elastic solid. Section 3 recapitulates the lattice Boltzmann scheme for the wave equation and provides the necessary information for the following implementations. The next section then introduces a macroscopic and a mesoscopic treatment of non-lattice-conforming boundary conditions. Lastly, numerical examples illustrate these implementations. Results for a stationary crack are shown and compared to analytical and previous numerical results. Furthermore, the propagation of a shear wave is examined in a more complex geometrical setup.

Fig. 1
figure 1

Antiplane shear deformation w(x, y, t) of a linear elastic solid with outer normal vector \({\varvec{n}}\) subjected to Neumann boundary conditions \({\varvec{t}}^*\) and Dirichlet boundary conditions \(w^*\). The outline of the body in the deformed configuration is indicated by dashed lines

Full size image

2 Antiplane shear deformation of a linear elastic solid

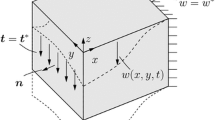
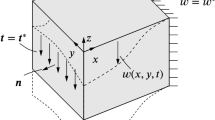
A homogeneous linear elastic body \({\mathcal {B}}\) with boundary \(\partial {\mathcal {B}}=\partial {\mathcal {B}}_w\cup {\mathcal {B}}_t\) subjected to Dirichlet boundary conditions on \(\partial {\mathcal {B}}_w\) and Neumann boundary conditions on \(\partial {\mathcal {B}}_t\) is considered, see Fig. 1. For the problem of antiplane shear deformation, the in-plane displacements are zero and the displacement field simplifies to \({\varvec{u}} = w(x,y,t) \, {\varvec{e}}_{z}\), where t is the time and \({\varvec{e}}_{z}\) describes the unit vector in z-direction. The evolution of w is given by the wave equation

$$\begin{aligned} \frac{\partial ^{2}w}{\partial x^{2}} + \frac{\partial ^{2}w}{\partial y^{2}} = \frac{1}{c_{s}^{2}} \frac{\partial ^{2}}{\partial t^{2}} w, \end{aligned}$$
(1)

where \(c_{s} = \sqrt{\nicefrac {\mu }{\rho }}\), with density \(\rho \), is the (macroscopic) wave speed of shear waves.

Eq. (1) describes the propagation of displacements w in \({\mathcal {B}}\). However, at the boundary \(\partial {\mathcal {B}}\) certain conditions have to be fulfilled. Two types are commonly used, namely Dirichlet and Neumann boundary conditions. Dirichlet-type conditions prescribe a displacement

$$\begin{aligned} w ({\varvec{x}}, {\varvec{y}}, t) = w^{*} ({\varvec{x}}, {\varvec{y}}, t) \end{aligned}$$
(2)

on \(\partial {\mathcal {B}}_{w}\), see Fig. 1, whereas Neumann-type conditions correspond to traction

$$\begin{aligned} \mu \left( \frac{\partial w}{\partial x} n_{x} + \frac{\partial w}{\partial y} n_{y} \right) {\varvec{e}}_{z} = t_{z}^{*} {\varvec{e}}_{z} = {\varvec{t}}^{*} \end{aligned}$$
(3)

or equivalently a prescribed gradient

$$\begin{aligned} \dfrac{\partial {w}}{\partial {{\varvec{x}}}}\cdot {\varvec{n}} = \dfrac{t_z^*}{\mu } = \dfrac{\partial {w}}{\partial {s}}^* \end{aligned}$$
(4)

on \(\partial {\mathcal {B}}_{t}\), see also Fig. 1. In the latter equation, \({\varvec{n}}\) refers to the normal vector at the boundary, and s is the arc length parameter for a line along the direction \({\varvec{n}}\) with s increasing in the direction of \({\varvec{n}}\).

3 Lattice Boltzmann implementation of the wave equation

This section introduces the lattice Boltzmann scheme for solving the wave equation, originally presented in [5]. The results are summarized here, providing only the information relevant to the following sections. A more detailed synopsis can also be found in [17].

Fig. 2
figure 2

a Lattice representation of the elastic solid and b the associated lattice velocity vectors (lattice links) for a single lattice point

Full size image

In the lattice Boltzmann method, the body \({\mathcal {B}}\) is represented by a 2D lattice \(\bar{{\mathcal {B}}}\) with uniform spacing \(\Delta h\), as displayed in Fig. 2. For the present case, each lattice point is linked to its four nearest neighbors, denoted by \({\alpha \in \left\{ 0,1,2,3,4 \right\} }\). The lattice Boltzmann method describes the evolution of the macroscopic fields, e.g., the displacement w, only indirectly. The primary quantities of the LBM are the so-called distribution functions \(f^{\alpha } ({\varvec{x}},t)\), which are each associated with a lattice direction \(\alpha \). The distribution functions \(f^{\alpha } ({\varvec{x}},t)\) are exchanged with lattice neighbors by means of the associated lattice velocity \({{\varvec{c}}^{\alpha }}\), which is defined as

$$\begin{aligned} \begin{aligned} {\varvec{c}}^{0}&=({c}^{0}_x,{c}^{0}_y)^{\mathop \intercal } = (0,0)^{\mathop \intercal }, \\ {\varvec{c}}^{1}&=({c}^{1}_x,{c}^{1}_y)^{\mathop \intercal } = (c,0)^{\mathop \intercal }, \qquad {\varvec{c}}^{2} =({c}^{2}_x,{c}^{2}_y)^{\mathop \intercal } = (0,c)^{\mathop \intercal }, \\ {\varvec{c}}^{3}&=({c}^{3}_x,{c}^{3}_y)^{\mathop \intercal } = (\text {-}c,0)^{\mathop \intercal }, \qquad {\varvec{c}}^{4} =({c}^{4}_x,{c}^{4}_y)^{\mathop \intercal } = (0,\text {-}c)^{\mathop \intercal }, \end{aligned} \end{aligned}$$
(5)

See Fig. 2b, where \(c = \nicefrac {\Delta h}{\Delta t}\) is the absolute value of the lattice velocity. Thus, the distribution functions reach the next site in one time step \(\Delta t\). Such a 2D lattice with five velocities is classified as a D2Q5 lattice Boltzmann model.

The continuum particle velocity \(\frac{\partial }{\partial t} w ({\varvec{x}},t) = {\dot{w}} ({\varvec{x}},t)\) is determined at the coordinate \({\varvec{x}}\) of a lattice point and at time t by means of the distribution functions

$$\begin{aligned} {\dot{w}} ({\varvec{x}},t) = \sum _{\alpha =0}^{4} f^{\alpha } ({\varvec{x}},t). \end{aligned}$$
(6)

Apart from transport to the nearest neighbors, the distribution functions also interact with other distribution functions at the particular lattice point. The latter is denoted by the collision of distribution functions. Transport and collision are both described by the lattice Boltzmann equation

$$\begin{aligned} f^{\alpha } \left( {\varvec{x}} + {\varvec{c}}^{\alpha } \Delta {t}, t + \Delta {t} \right) = f^{\alpha } ({\varvec{x}},t) - \underbrace{\frac{1}{\tau } \left[ f^{\alpha } ({\varvec{x}},t) - f^{\alpha }_{\text {eq}} ({\varvec{x}},t) \right] }_{\text {collision}}, \end{aligned}$$
(7)

where the relaxation time \(\tau >0\) and the equilibrium distributions \(f^{\alpha }_{\text {eq}}\) determine the particular physics that are simulated, e.g., the wave equation (1).

In 2D the equilibrium distribution functions according to the model of [5] for the wave equation are

$$\begin{aligned} \begin{aligned} f_\text {eq}^0&= \frac{\partial w}{\partial t} - \frac{2 \lambda w}{c^2},\quad {\lambda =\dfrac{c_s^2}{\Delta {t}\left( \tau -\dfrac{1}{2}\right) }}, \\ f_\text {eq}^{k}&= \frac{\lambda w}{c^2} \quad \text {for } k \in \{ 1,2,3,4 \}. \end{aligned} \end{aligned}$$
(8)

The displacement w is determined in a post-processing step after the distribution functions and the corresponding particle velocity \({\dot{w}}\) are determined by (1) and (6), respectively. An implicit Euler scheme is used to obtain the displacement via

$$\begin{aligned} w ({\varvec{x}}, t+\Delta {t}) = w ({\varvec{x}}, t ) + \Delta t \; {\dot{w}} ({\varvec{x}}, t+\Delta {t}). \end{aligned}$$
(9)

4 Non-lattice-conforming boundary conditions

The lattice Boltzmann Eq. (7) is able to determine the evolution of the distribution functions, and thus also the evolution of the macroscopic displacement, in the interior of the domain. However, lattice points at the boundary miss one or more lattice links, i.e., neighbor lattice points. These lattice points are denoted as boundary lattice points \({\varvec{x}}_B\). For boundary lattice points, not all distribution functions can be obtained from collision and streaming, i.e., by the lattice Boltzmann equation (7). Instead, the missing distribution functions have to be determined by the boundary conditions.

A simple but effective strategy is the so-called bounce-back strategy where the missing distribution functions are just set to the value of the distribution function associated with the lattice speed in the opposite direction. For LBM that treat fluid flows, the bounce-back typically corresponds to a non-slip wall, which is a very common type of boundary condition in fluid mechanics. For more complicate situations, e.g., curved or moving boundaries, more elaborate schemes have been introduced, such as immersed [18] or implicit [19] boundaries. However, if a solid is considered, the way of posing the boundary problem is different. One would like to specify displacements and traction, i.e., the gradient of the displacement, and it is not obvious how the bounce-back should be modified in order to satisfy those constraints, or how other boundary conditions would fit in the requirements of solid mechanics.

This motivated the strategy proposed in our previous work [17], where the missing distribution functions are computed such that the desired macroscopic boundary conditions are fulfilled. The drawback of this strategy is that the lattice is required to conform to the considered domain, i.e., the boundary lattice points need to coincide with the boundary

$$\begin{aligned} {\varvec{x}}_B \in \partial {{{{\mathcal {B}}}}}, \quad \forall {{\varvec{x}}_B}. \end{aligned}$$
(10)

Since the lattice is required to be strictly regular, this limits the geometries that can be modeled. In [17], this leads to the simplification that a crack needs to be modeled as a notch of finite width which contradicts the assumptions of a benchmark analytical solution also discussed in [17]. To address this shortcoming, two alternative approaches to treat boundary conditions are presented in this section that do not require the lattice to conform with the boundary.

Fig. 3
figure 3

A section of the considered body where non-lattice-conforming boundary conditions are applied at boundary lattice point \({\varvec{x}}_B\)

Full size image

4.1 Macroscopic implementation

The first strategy is similar to the one shown in [17]. However, it is now allowed that the bounding geometry does not exactly coincide with lattice points and can be rather independent of the underlying lattice. We refer to this strategy as a non-lattice-conforming implementation of the boundary conditions.

Figure 3 illustrates the algorithm for a particular boundary lattice point that clearly does not lie on the boundary itself. As a first step, the closest point on the boundary (blue point) is computed for each boundary lattice point (red points). Subsequently, an auxiliary line (dotted line) is constructed by the boundary lattice point and the associated nearest boundary point. The direction of the line is given by the outward normal vector \({\varvec{n}}\) at the boundary point. We parametrize the line by the arc length parameter s, where \(s=0\) at the boundary point and s increases in the outward normal direction. Along this line, a polynomial of second order is defined

$$\begin{aligned} {\tilde{w}}_{t+\Delta {t}}: [0,-2\Delta {h}] \rightarrow {\mathbb {R}}, \quad {\tilde{w}}_{t+\Delta {t}} = as^2+bs+c \end{aligned}$$
(11)

that approximates the displacement field at time \(t+\Delta {t}\).

A prescribed Neumann boundary condition \(\frac{\partial {w}}{\partial {s}}^*({\varvec{x}}_{CB}, t+\Delta {t})\) at the boundary point \({\varvec{x}}_B\) corresponds to the constraint

$$\begin{aligned} \dfrac{\partial {w}}{\partial {s}}({\varvec{x}}_{CB},t+\Delta {t}) = {\tilde{w}}'_{t+\Delta {t}}(0)= \dfrac{\partial {w}}{\partial {s}}^*({\varvec{x}}_{CB}, t+\Delta {t}), \end{aligned}$$
(12)

whereas a Dirichlet boundary condition reads

$$\begin{aligned} w({\varvec{x}}_{CB}) = {\tilde{w}}_{t+\Delta {t}}(0) = w^*({\varvec{x}}_{CB}, t+\Delta {t}). \end{aligned}$$
(13)

The constraints (12) and (13) are complemented by the condition that the polynomial must match the displacement at two interior points which are located at

$$\begin{aligned} {\varvec{x}}_{I} = {\varvec{x}}_{BC} - \Delta {h}{\varvec{n}} \end{aligned}$$
(14)

and

$$\begin{aligned} {\varvec{x}}_{II} = {\varvec{x}}_{BC} - 2\Delta {h}{\varvec{n}}. \end{aligned}$$
(15)

Thus, it is required that

$$\begin{aligned} {\tilde{w}}(-\Delta {h}) = w({\varvec{x}}_I, t+\Delta {t}) \end{aligned}$$
(16)

and

$$\begin{aligned} {\tilde{w}}(-2\Delta {h}) = w({\varvec{x}}_{II}, t+\Delta {t}). \end{aligned}$$
(17)

Consequently, three constraints are available that allow to determine the coefficients a, b, and c of \({\tilde{w}}\). In order to determine the unknown displacement at \({\varvec{x}}_B\) in a fashion that is consistent with the macroscopic boundary conditions, the polynomial \({\tilde{w}}\) is evaluated at the boundary lattice point

$$\begin{aligned} {\varvec{x}}_B={\varvec{x}}_{BC}-q{\varvec{n}}, \end{aligned}$$
(18)

where q is the shortest distance of \({\varvec{x}}_B\) to the boundary, i.e., after rearranging terms

$$\begin{aligned} \begin{aligned} w({\varvec{x}}_B, t+\Delta {t})&= {\tilde{w}}(-q) \\&= w_I(t+\Delta {t}) \underbrace{\left[ -\dfrac{q^2}{3\Delta {h}^2}+ \dfrac{4}{3}\right] }_{A_B} + w_{II}(t+\Delta {t})\underbrace{\left[ \dfrac{q^2}{2\Delta {h}^2}-\dfrac{1}{3}\right] }_{B_B} \\&\quad + \underbrace{\dfrac{\partial {w}}{\partial {s}}^*({\varvec{x}}_{BC}, t+\Delta {t})\left[ \dfrac{q^2}{3\Delta {h}}-q + \dfrac{2\Delta {h}}{3}\right] }_{C_B} \end{aligned} \end{aligned}$$
(19)

for Neumann boundary conditions and

$$\begin{aligned} \begin{aligned} w({\varvec{x}}_B, t+\Delta {t})&= {\tilde{w}}(-q) \\&= w_I(t+\Delta {t})\underbrace{\left[ -\dfrac{q^2}{\Delta {h}^2}+2\dfrac{q}{\Delta {h}}\right] }_{A_B} + w_{II}(t+\Delta {t})\underbrace{\left[ \dfrac{q^2}{2\Delta {h}^2}-\dfrac{q}{2\Delta {h}}\right] }_{B_B} \\&\quad + \underbrace{w^*({\varvec{x}}_{BC},t+\Delta {t})\left[ \dfrac{q^2}{2\Delta {h}^2}-\dfrac{3q}{2\Delta {h}}+1\right] }_{C_B} \end{aligned} \end{aligned}$$
(20)

for Dirichlet boundary conditions.

Note that \({\varvec{x}}_I\) and \({\varvec{x}}_{II}\) have to lie inside the considered domain which is guaranteed if the material is at least \(2\Delta {h}\) thick in the direction normal to any boundary. If that is not the case, e.g., for sharp (\(< 90^\circ \)) corners, the domain has to be modified, see Fig. 4. This can be accomplished by defining zones of \(2\Delta {h}\) width for each boundary segment which are shown as red and blue dashed lines in Fig. 4a. The union of all of these zones has to be part of the domain \({{{\mathcal {B}}}}\). If that is not the case, the responsible boundary segments have to be modified. In Fig. 4a, the light gray shaded region is removed to obtain the valid domain in Fig. 4b.

Fig. 4
figure 4

a A section of a domain \({{{\mathcal {B}}}}\) for which the macroscopic implementation for non-lattice-conforming boundary conditions cannot be utilized and b a modified geometry that allows to utilize the macroscopic implementation for non-lattice-conforming boundary conditions

Full size image

The points \({\varvec{x}}_{I}\) and \({\varvec{x}}_{II}\) generally do not coincide with lattice points. Thus, the displacement \(w({\varvec{x}}_I,t+\Delta {t})\) and \(w({\varvec{x}}_{II},t+\Delta {t})\) need to be interpolated. To this end, two quadratic cells \(C_{I}\) and \(C_{II}\) that contain \({\varvec{x}}_I\) and \({\varvec{x}}_{II}\), respectively, are considered, see Fig. 3. Within these cells bilinear interpolation is used to obtain \(w({\varvec{x}}_I,t+\Delta {t})\) and \(w({\varvec{x}}_{II},t+\Delta {t})\) from the current values of the corner points. The interpolated value is thus dependent on all lattice points constituting the cells corner points. We refer to these sets of lattice points as \({{{\mathcal {P}}}}_I\) and \({{{\mathcal {P}}}}_{II}\). Thus, we can compute the displacements at \({\varvec{x}}_{I}\) and \({\varvec{x}}_{II}\) from

$$\begin{aligned} \begin{aligned} w({\varvec{x}}_I,t+\Delta {t})&= \sum _{p\in {{{\mathcal {P}}}}_{I}}a({\varvec{x}}_{I},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}), \\ w({\varvec{x}}_{II},t+\Delta {t})&= \sum _{p\in {{{\mathcal {P}}}}_{II}}a({\varvec{x}}_{II},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}) \end{aligned} \end{aligned}$$
(21)

where \(a({\varvec{x}}_{I},{\varvec{x}}_p)\) and \(a({\varvec{x}}_{II},{\varvec{x}}_p)\) are the interpolation coefficients which only depend on the regarded geometry and the lattice. Note that the corner points of each cell may be part of the set of boundary lattice points Bd as well.

Substituting (21) into (19) or (20), respectively, yields an equation of the form

$$\begin{aligned} \begin{aligned}&w({\varvec{x}}_B, t+\Delta {t}) - A_B\sum _{p\in {{{\mathcal {P}}}}_I, p \in {Bd}} a({\varvec{x}}_{I},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}) \\&\qquad - B_B\sum _{p\in {{{\mathcal {P}}}}_{II}, p \in {Bd}} a({\varvec{x}}_{II},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}) \end{aligned} \nonumber \\ \left. \begin{aligned}&\quad = A_B \sum _{p\in {{{\mathcal {P}}}}_I, p \notin {Bd}} a({\varvec{x}}_{I},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}) \\&\qquad + B_B\sum _{p\in {{{\mathcal {P}}}}_{II}, p \notin {Bd}} a({\varvec{x}}_{II},{\varvec{x}}_p)w({\varvec{x}}_p,t+\Delta {t}) + C_B \end{aligned} \right\} =:R_B(t+\Delta {t}) \end{aligned}$$
(22)

where again Bd denotes the set of all boundary lattice points. This can be recast in a linear equation as

$$\begin{aligned} \sum _{\left( p\in {{{\mathcal {P}}}}_I \vee p \in {{{\mathcal {P}}}}_{II}\right) \wedge (p \in {Bd}) } S_{Bp} w({\varvec{x}}_p, t+\Delta {t}) = R_{B}(t+\Delta {t}). \end{aligned}$$
(23)

Herein, the coefficients of the unknown displacement at the boundary points \(S_{Bp}\) only depend on the geometry and the lattice setup. They do not depend on time. In contrast, the right-hand side \(R_B\) also depends on the geometry and the lattice but involves the current displacement at interior lattice points and the currently applied boundary condition at \({\varvec{x}}_{BC}\) as well. Consequently, the time-dependent part of the right-hand side \(R_B\) needs to be assembled in every time step, whereas the coefficients \(S_{Bp}\) do not. Forming equation (23) for each boundary lattice points results in a linear system of equations

$$\begin{aligned} {\varvec{S}}{\varvec{w}}_B(t+\Delta {t}) = {\varvec{R}}(t+\Delta {t}) \end{aligned}$$
(24)

that can be solved for the unknown displacements \({\varvec{w}}_B\) of all boundary lattice points. In general, the cardinality of Bd is much smaller than the total number of lattice points. Thus, the effort to solve this system of equations is relatively small. Furthermore, the matrix \({\varvec{S}}\) only needs to be assembled and inverted once. After \({\varvec{S}}^{-1}\) is available, \({\varvec{w}}_B\) is obtained through a simple matrix multiplication

$$\begin{aligned} {\varvec{w}}_B = {\varvec{S}}^{-1}{\varvec{R}}(t+\Delta {t}). \end{aligned}$$
(25)

Once \(w({\varvec{x}}_B,t+\Delta {t})\) is known at each boundary lattice point \({\varvec{x}}_B\), the missing distribution functions can be determined such that they are consistent with \(w({\varvec{x}}_B,t+\Delta {t})\). We denote the set of functions at \({\varvec{x}}_B\) that can be determined from (7), i.e., by collision and streaming, as the set of known distribution functions \({{\mathcal {F}}}_{{\varvec{x}}_B}\) and the number of missing distribution functions as \( n_{\text {miss}} = 5- \vert {{{\mathcal {F}}}}_{{\varvec{x}}_B} \vert \). Each missing distribution function is set to

$$\begin{aligned} \begin{aligned}&f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) = f_{\text {miss}} \\&\quad = \dfrac{1}{n_\text {miss}}\left[ \dfrac{w({\varvec{x}}_B, t+\Delta {t}) - w({\varvec{x}}_B, t)}{\Delta {t}}-\sum _{\beta \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}}f^{\beta }({\varvec{x}}_{B},t+\Delta {t})\right] , \quad \forall \alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B} \end{aligned} \end{aligned}$$
(26)

which will guarantee that \(w({\varvec{x}}_B,t+\Delta {t})\) is consistent with the definition of the distribution functions (6) as well as the integration rule (9). Note that (26) depends on the definition of the distribution functions and will thus be slightly different for other LBMs for the wave equation, as, e.g., the model presented in [20].

In (26) only the missing distribution functions are modified due to the applied boundary conditions. This approach seems natural since the other distribution functions can be determined by (7) and therefore represent a normal interaction with the surrounding material that should not be interfered with. However, if one only desires to derive set of distribution functions that is consistent with the macroscopic displacement, it is also possible to set all distribution functions to be equal to the equilibrium distribution at the desired displacement, i.e.,

$$\begin{aligned} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) = f^{\alpha }_{\text {eq}}(w({\varvec{x}}_B, t+\Delta {t})), \quad \forall \alpha . \end{aligned}$$
(27)

This option is described, e.g., in [21]. However, in the present work, we employ the first option (26).

The overall algorithm is displayed in Alg. 1. The part of the algorithm that deals with the implementation of the boundary conditions determines the macroscopic field \(w({\varvec{x}}_B,t+\Delta {t})\) at each boundary lattice point such that it is consistent with the boundary conditions on the macroscopic scale. This is why, we refer to the algorithm as a ‘macroscopic’ algorithm for the treatment of the boundary conditions.

figure a
Fig. 5
figure 5

Boundary cells for the mesoscopic treatment of Neumann boundary conditions

Full size image

4.2 Mesoscopic implementation of Neumann Boundary Conditions

By relation (6), the distribution functions are strongly related to the momentum density, i.e.,

$$\begin{aligned} \rho {\dot{w}}({\varvec{x}},t)=\rho \sum _{\alpha =0}^{4} f^\alpha ({\varvec{x}}, t+\Delta {t}). \end{aligned}$$
(28)

In order to derive an alternative approach to define Neumann boundary conditions at a boundary lattice point \({\varvec{x}}_B\), we consider a small material volume, i.e., a cell of size \(V_C\), that is centered around the lattice point and also intends to match the boundary as depicted in Fig. 5. This cell shares part of the external boundary \(A_C\subset \partial {{{\mathcal {B}}}}\). The cell does not exactly match the geometry of the considered body and thus the external traction that is applied to the boundary cell is only an approximation of the traction applied to the real geometry. Let us assume that the approximated external traction applied at \(A_C\) is

$$\begin{aligned} \int _{\partial {A_C}} {\varvec{t}}^* \mathrm{d}A \approx {\varvec{T}}_{C}^{\text {ext}} = {T}_{C}^{\text {ext}} {\varvec{e}}_z. \end{aligned}$$
(29)

Further, assuming that the momentum \(P_C\) of such a cell is approximately

$$\begin{aligned} P_C {\; \approx \;} V_C\rho {\dot{w}}({\varvec{x}}_{B}, t). \end{aligned}$$
(30)

The change of momentum of such a cell in one time step can be expressed as

$$\begin{aligned} \rho {V_C}\dfrac{{\dot{w}}({\varvec{x}}_{B}, t+\Delta {t})-{\dot{w}}({\varvec{x}}_{B}, t)}{\Delta {t}} = {T}_C^{\text {ext}} + {T}_C^{\text {int}}. \end{aligned}$$
(31)

Herein, \({T}_C^{\text {int}}\) is the internal traction that is applied to cell C via the surrounding material, i.e., the blue cells in Fig. 5. This motivates to identify the change of velocity caused by \({T}_C^{\text {int}}\) in one time step with

$$\begin{aligned} \dfrac{{T}_C^{\text {int}}\Delta {t}}{\rho {V}_C} = \sum _{\alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}\setminus \{0\}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) - \sum _{\alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}\setminus \{0\}} f^{\alpha }({\varvec{x}}_B,t), \end{aligned}$$
(32)

i.e., it is the change of distribution functions that are streamed to \({\varvec{x}}_B\) from its neighbors over one time step. Substituting (32) into (31) yields

$$\begin{aligned} \begin{aligned}&\sum _{ \alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t})+\sum _{ \alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) \\&\quad = \dfrac{{T}_C^{\text {ext}}\Delta {t}}{\rho {V_C}} + {\dot{w}}({\varvec{x}}_B, t) +\sum _{\alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}\setminus \{0\}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) - \sum _{\alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}\setminus \{0\}} f^{\alpha }({\varvec{x}}_B,t) \end{aligned} \end{aligned}$$
(33)

and finally

$$\begin{aligned} \begin{aligned}&\sum _{ \alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) = \dfrac{{T}_C^{\text {ext}}\Delta {t}}{\rho {V_C}} + {\dot{w}}({\varvec{x}}_B, t) -f^{0}({\varvec{x}}_B,t+\Delta {t})- \sum _{\alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}\setminus \{0\}} f^{\alpha }({\varvec{x}}_B,t) \end{aligned} \end{aligned}$$
(34)

Thus, the sum of the previously unknown distribution functions can be computed from (34) such that it is consistent with a balance of momentum for the cell \(V_C\). Once the sum of unknown distribution functions is determined, one can compute the value of the missing distribution functions by equally distributing to all missing distribution functions

$$\begin{aligned} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) = \dfrac{1}{n_{\text {miss}}} \left[ \sum _{\alpha =0, \alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t})\right] , \quad \forall {\alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B}} \end{aligned}$$
(35)

Since this variant of an implementation of boundary conditions does not start with a desired macroscopic value of \(w({\varvec{x}}_B, t+\Delta {t})\) but considers a balance of momentum at a mesoscopic scale, i.e., at the level of lattice points, we denote this variant as a mesoscopic implementation of the boundary conditions.

This approach has a distinct advantage over the previously mentioned macroscopic method, since it does not require the solution of a system of equations and is purely local. This is particularly useful for parallel computations in which each boundary lattice point can be treated independent of all other lattice points. Such parallelization is not possible for the macroscopic treatment of the boundary conditions.

Unfortunately, this approach is only available for Neumann boundary conditions. Dirichlet boundary conditions cannot be implemented since the applied reaction force that is required to obtain the desired \(w^*\) at the non-lattice-conforming boundary \({\varvec{x}}_{BC}\) is not known. The only thing that can be done in such a situation is to assume that the boundary is lattice conforming \({\varvec{x}}_{B} = {\varvec{x}}_{BC}\) and use the approach discussed in our previous work [17], i.e., to compute the sum of missing distribution functions from

$$\begin{aligned} \sum _{ \alpha \notin {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}) = \dfrac{w^{*}({\varvec{x}}_B, t+\Delta {t}-w({\varvec{x}}_B, t)}{\Delta {t}}-\sum _{ \alpha \in {{{\mathcal {F}}}}_{{\varvec{x}}_B}} f^{\alpha }({\varvec{x}}_B,t+\Delta {t}). \end{aligned}$$
(36)

Furthermore, an adaptation of the mesoscopic approach to other types of LBMs for wave equations such as, e.g., the model of [20] is not straightforward since their physical interpretation of the distribution functions is not directly linked to the momentum as in (28).

The overall algorithm for the mesoscopic implementation of Neumann boundary conditions is shown in Alg. 2. The only changes concern the treatment of the boundary conditions and the preprocessing of the geometry that is required to handle the different implementations.

Note that both implementations can also be combined. For example, it is possible to use the mesoscopic implementation to define zero Neumann boundary conditions at a crack inside the body and define all boundary conditions that are applied to the external boundary via the macroscopic implementation. Such a hybrid implementation of boundary conditions is applied for the second numerical example of the next section.

figure b

5 Numerical examples

In this section, the capabilities of the discussed enhanced treatment of boundary conditions are demonstrated by two numerical experiments. The first experiment demonstrates that the new algorithms indeed improve the results we obtained in [17] for the elastic fields close to the crack tip of a dynamically loaded stationary crack.

The second example highlights that the new methods are able to handle more general geometries. In particular, a geometry partly composed of circles and circle segments is considered that cannot be captured exactly by a mesh-conforming treatment of boundary conditions.

5.1 Instantaneous antiplane shear loading of a stationary crack

The first numerical experiment is concerned with simulating the elastic fields near a dynamically loaded crack. A feature of classical fracture mechanics is that cracks are assumed to be cuts of zero thickness in the material, i.e., in the undeformed state the crack faces have identical position. In general, the displacement field is discontinuous across open cracks and singular stresses appear at the crack tips if the body is loaded. Irwin found that the mechanical fields in the vicinity of the crack tip are universal except for three variables, the stress intensity factors (SIF), which depend on the specific geometry and loading situation [22]. In case of pure antiplane shear deformation, the fields are determined by only one stress intensity factor K(t).

In [17], we studied how well the LBM for the wave equation of [5] is able to predict the elastic fields near the crack tip, i.e., how well the SIF K(t) can be predicted. This is possible since the behavior of an elastic solid is described by the wave equation in the case of antiplane shear deformation as is shown in section two. In this work, we study the same problem in order to demonstrate the enhanced treatment of boundary conditions that is available due to the two approaches discussed in the previous section. We compare these results to our previous work reported in [17] and, as before, also to an analytical solution and FEM simulations.

The analytical solution obtained by Burridge [23] and Thau and Lu [24] considers a straight and stationary crack of length 2L and zero thickness in an infinite elastic medium with shear modulus \(\mu \) and wave speed \(c_s\), see Fig. 6a. The crack faces are subjected to an instantaneous uniform load of

$$\begin{aligned} \sigma _{xz}=-t_z^*H(t), \end{aligned}$$
(37)

where H(t) is the Heaviside function and \(t_z^*=0.0025\mu \frac{w_r}{L}\) is the magnitude of the applied traction and \(w_r\) a reference displacement. The resulting analytical expression of the dynamic stress intensity factor is

$$\begin{aligned} \dfrac{K({\hat{t}})}{K_{s}}=\dfrac{4}{\pi }\left[ \sqrt{{\hat{t}}}-\dfrac{1}{\pi }H({\hat{t}}-1)I({\hat{t}})\right] , \quad (0\le {{\hat{t}}}\le {2}) \end{aligned}$$
(38)

where \(K_s=\displaystyle \lim _{t\rightarrow {\infty }}K(t)=t_z^*\sqrt{\pi {L}}\) is the static limit of the SIF, \({\hat{t}}=\frac{c_st}{2L}\) is the dimensionless time and

$$\begin{aligned} I({\hat{t}})=\displaystyle \int _{1}^{{\hat{t}}}\dfrac{1}{\alpha }\sqrt{\dfrac{({\hat{t}}-\alpha )(\alpha +1)}{\alpha -1}}\ \mathrm {d}\alpha . \end{aligned}$$
(39)

In contrast to the analytical solution for an infinite elastic medium, the computational domain has a finite size of \(8L\times 8L\), where the element size in the FEM simulations is four times as coarse as the lattice spacing used in the LBM simulations, i.e., \(\Delta {h}_{\text {FEM}}=4\Delta {h}=\frac{8L}{336}\). Since the domain is still large enough to guarantee that reflection of waves at the boundary does not influence the results at the crack tip in the considered time interval, we do not expect any deviation from the analytic solution because of the finite size of the computational domain. The boundaries are assumed to be stress-free, i.e., \({t}_z={0}\) and the crack faces are subjected to a sudden traction load as defined in (37). The microscopic lattice wave speed is set to \(c=7.5c_s\) and the relaxation time is set to \(\tau =1.0\frac{\Delta {h}}{c}\). The time step is determined by the lattice speed c and the lattice spacing \(\Delta {h}\) as \(\Delta {t}=\frac{\Delta {h}}{c}=\frac{8L}{4\cdot 336\cdot 7.5c_s}\). The time step used in the explicit central difference scheme of the FEM computations is four times as large, i.e., \(\Delta {t}_{\text {FEM}}=\frac{8L}{336\cdot 7.5c_s}\). The shape functions in the FEM simulations are bilinear.

A major difficulty in modeling a crack with the LBM as used in [17] is that it fails to model cracks of zero width. This is due to the fact that the lattice points are required to lie on the boundary of the regarded body by the implementation of boundary conditions in [17], i.e., the geometry needs to ‘conform’ with the lattice. In the original model, a lattice point at the crack tip would be associated with five nearest neighbors—one additional neighbor due to the two crack faces that occupy the same surface in material space—and consequently it is unclear how the streaming from and to the crack tip should be handled. As a consequence, cracks can only be modeled as notches of finite width, see Figs. 6b and 7a. It follows that cracks need to be at least one lattice spacing \(\Delta {h}\) wide. This results in a systematical underestimation of the stiffness of the specimen by the LBM. However, due to the new approaches introduced in section four, it is now possible to model a geometry that is non-lattice conforming within the LBM. Thus, a crack of zero thickness can be represented in a straightforward manner, as shown in Fig. 6b, c.

Fig. 6
figure 6

a Antiplane shear loaded crack in an infinite elastic medium, b computational model for the LBM simulations in [17] (notch model), and c the computational model for the LBM and FEM simulations presented in this work

Full size image
Fig. 7
figure 7

a A detailed view of the computational model for the LBM simulation in [17] (notch model) which also shows the locations at which the displacement jump across the crack is evaluated. A detailed view of the computational model for the LBM simulations with the macroscopic (b) and mesoscopic (c) treatment of non-lattice-conforming boundary conditions. The arrows in b) and c) indicate that the displacement is extrapolated in order to determine the displacement jump across the crack

Full size image
Fig. 8
figure 8

Contour plots of w for the LBM simulations with non-lattice-conforming treatment of the boundary conditions at a \({\hat{t}}\approx 0.14\), b \({\hat{t}}=1.0\) (peak stress intensity factor), and at c \({\hat{t}}\approx 1.57\). The reference displacement is set to \(w_r=L\), but the deformation is scaled by factor 100 in the plots

Full size image
Fig. 9
figure 9

Graph of the SIF evaluated at different distances from the crack tip a for the LBM notch model from [17] with \(\tau =1.0\frac{\Delta {h}}{c}\), b for the LBM crack model with the macroscopic formulation of non-lattice-conforming boundary conditions, c for the LBM crack model with mesoscopic formulation of the non-lattice-conforming boundary conditions, and d for the FEM crack model

Full size image

From the simulations, the SIF is found by evaluating the displacement jump \(\delta \) across the crack close to the crack tip, i.e., at distances of \(r=\Delta {h}_{\text {FEM}}\) to \(r=3\Delta {h}_{\text {FEM}}\) for all computations except the mesoscopic model for which \(\delta \) is evaluated at \(r=0.875\Delta {h}_{\text {FEM}}\) to \(r=2.875\Delta {h}_{\text {FEM}}\),

$$\begin{aligned} \delta (r) = \vert {w}^+(r)-w^-(r){\vert }, \end{aligned}$$
(40)

where r is the distance from the crack tip and \(+/-\) indicate that the displacement is evaluated at two different crack faces.

In the FEM simulations, this is done by computing the difference of the displacement at nodes which are located at the same position but at opposing crack faces. In the LBM simulations with the notch model, this is done by evaluating the displacement at opposing sides of the notch as shown in Fig. 7a. In the LBM simulations with the enhanced boundary condition treatment, the displacement field is extrapolated to the crack faces by means of the applied traction and the current displacement at lattice points, see Fig. 7b, c. This is done by evaluating the polynomial (11) at \(s=0\). This extrapolation is not justifiable in the LBM notch model as proposed in [17], as the traction is also applied at the notch edges, but seems suitable if a crack is modeled by either the macroscopic or mesoscopic boundary condition treatment.

Once the displacement jump is known, the SIF can eventually be computed from

$$\begin{aligned} K(t)\approx \delta (r,t)\dfrac{\mu }{4}\sqrt{\dfrac{2\pi }{r}}, \quad r\ll {L}, \end{aligned}$$
(41)

see [23, 24].

Figure 8 gives an impression on how the loading affects the displacement field of in the specimen. This is very similar for both implementations of non-lattice-conforming boundary conditions. Consequently, only the plots for the macroscopic implementation are displayed. As the load is applied, a wave emanates from the crack faces and interacts with the crack surfaces. The crack opens steadily and thus the SIF at both crack tips is expected to increase until at \({\hat{t}}=1\) the presence of the other crack tip is ‘felt,’ see also the red lines in Fig. 9. The analytic solution states that at this time the SIF starts to decrease again.

In Fig. 9, the stress intensity factor according to the analytical solution, the LBM notch model, the LBM crack models with enhanced treatment of boundary conditions, and the FEM model are shown. It can be observed that the FEM results overestimate the specimens’ stiffness which results in an underestimation of the stress intensity factor compared to the analytical solution. The LBM on the other hand generally underestimates the stiffness of the material and thus overestimates the stress intensity factor. Nonetheless, both enhanced formulations of the boundary conditions noticeably improve the results obtained from the LBM notch model, which may also partly be attributed to the extrapolation mentioned above. Overall the relative error of the peak SIF, i.e., at \({\hat{t}}=1\), when the SIF is evaluated from the displacement jump at a distance of \(3\Delta {h}\) is reduced from \(4.59\%\) for the LBM notch model to \(2.24\%\) for the macroscopic and \(2.64\%\) for the mesoscopic boundary condition implementations, respectively.

Notably, all LBM simulations are more accurate than the benchmark FEM simulation with a relative error of the peak SIF of \(5.1\%\). A major cause for this is of course the much finer spatial and temporal resolution of the LBM computations, \(\Delta {h}_{\text {FEM}} = 4\Delta {h}, \Delta {t}_{\text {FEM}} = 4\Delta {t}\). However, the improved accuracy of the LBM simulations does not come with an increased runtime of the simulations. As already reported in [17], the FORTRAN-coded FEM simulations took 142193s (\(\sim \)40h) to complete when run on a conventional CPU, i.e., Intel Core i7-3770 3.40GHz. The runtimes of the LBM simulations on the same hardware are 96446s (\(\sim \)27h) for the notch model, 97426s (\(\sim \)27h) for the macroscopic treatment of the boundary conditions, and 94458s (\(\sim \)26h) for the mesoscopic treatment of the boundary conditions.

5.2 Propagation of a shear wave with a non-trivial geometry

Fig. 10
figure 10

The setup for the numerical example of shear wave propagation. The geometry of the domain is illustrated in (a). The boundary conditions are color-coded, with homogeneous Dirichlet boundary conditions in green and homogeneous Neumann boundary conditions in blue. Purple indicates the boundary which excites the initial wave through a time-dependent Neumann-type condition. The three markers show the positions of the points for which results are given in Fig. 13. The section displayed in (b) is indicted by the red corners. b shows lattice points with associated cells at the boundary in the lower left part of the domain. The spacing is reduced to \(\Delta h = \nicefrac {L}{8}\). The outer edges of the cells coincide with the boundary. c shows the Ricker wavelet \(\psi (t)\) defined in Eq. (42) for a simulation time of \(0 \le {\hat{t}} < 2\). For later times \(\psi \) remains at zero. This wavelet is responsible for the initial wave. (Color figure online)

Full size image
Fig. 11
figure 11

The mesh of the FE-simulation is composed of four parts to accommodate the geometry of the computational domain

Full size image
Fig. 12
figure 12

Contour plots of the displacement w at four points in time for the two LBM implementations and for the FEM. The columns show the different instances in time, given in terms of the dimensionless simulation time (\(0 \le {\hat{t}} \le 12\)); The rows depict the different numerical methods: the LBM with the meso- and macroscopic implementations and the FEM for comparison

Full size image

An additional numerical example showcases the possibilities of the presented implementations of boundary conditions. For this purpose, the propagation of an elastic shear wave in a non-trivial domain is regarded. The computational domain has a finite size of \(8L \times 8L\), where L is an arbitrary reference length. The material parameters are given as \(\mu \) and \(c_s\). The lattice spacing is chosen as \(\Delta h = \nicefrac {L}{32}\). The time step is then \(\Delta t = \nicefrac {\Delta h}{7.5 \cdot c_s} = \nicefrac {L}{32 \cdot 7.5 \cdot c_s}\). The time is given in terms of the dimensionless simulation time \({\hat{t}} = t \; \nicefrac {c_s}{L}\). Figure 12 illustrates the geometry of this domain and the three different boundary conditions that are employed: the lower and left edges are held fixed by a Dirichlet boundary condition prescribing zero displacement (in green); the right and top edges are connected by a circle segment and are free boundaries with a Neumann-type condition of zero traction (in blue). Additionally, a circular hole is cut out in the center of the lower left quadrant. Here a Neumann boundary condition (in purple) prescribes a time-dependent traction \(t^{*}_{z} ({\hat{t}}) = t^{*}_{z} \; \psi ({\hat{t}}) \; {\varvec{e}}_z\), which excites the initial elastic wave. The time dependency is defined by a Ricker wavelet [25]

$$\begin{aligned} \psi (t) = \frac{2}{(3 \sigma )^2 \, \pi ^4} \left( 1- \left( \frac{t-t'}{\sigma } \right) ^2 \right) \exp \left( -\frac{1}{2} \left( \frac{t-t'}{\sigma } \right) ^2 \right) , \end{aligned}$$
(42)

where \(t^{*}_0 = 1 \mu \frac{w_r}{L}\). The parameter \(\sigma = 0.215\) scales the width and \({\hat{t}}^{\prime } = 1\) shifts the maximum, see Fig. 10c.

Both the circular hole and the outer circle segment could not be modeled exactly by mesh-conforming boundary conditions. This can be seen for a section in the lower left part of the domain in Fig. 10b. It shows the lattice points (in blue), with a reduced lattice spacing of \(\Delta h = \frac{L}{8}\), and the cells of the boundary lattice cells for the mesoscopic implementation (in red).

Fig. 13
figure 13

The displacement w over time evaluated at three different points (as marked in Fig. 10a) for the two LBM implementations (solid red and blue) and for the FEM (solid black) for comparison. The dotted lines show the absolute deviation of the LBM results from the FEM at these points. (Color figure online)

Full size image

This example is solved numerically by means of the LBM with the meso- and macroscopic implementation of the non-mesh-conforming boundary conditions described in Sect. 4. But since there is no formulation for Dirichlet-type conditions in the mesoscopic implementation, the macroscopic formulation was used instead. What is called mesoscopic here is therefore actually a mix of both implementations. Lacking an analytical solution, numerical results have also been obtained by the FEM for comparison. Since the FEM is an accepted standard tool in engineering, and it is suitable as a benchmark. The mesh of the FE computation is shown in Fig. 11. The shape functions are bilinear and the standard Newmark scheme is employed for integration.

The results of all three simulations are illustrated in Fig. 12 as contour plots of the displacement w at four selected instances of time. All numerical strategies predict the circular wave expanding outward from the hole at \({\hat{t}} = 1.5\) The first reflection occurs at the fixed boundary and whereas the wave reaches the other edges of the domain at later times. A complex pattern emerges, consisting of superposed reflected waves traveling in different directions.

In addition to the instantaneous contour plots, Fig. 13 shows the displacement w over the simulation time for each of the three points indicated in Fig. 10a. The coordinates are \({(-3.02L, -2.02L)}\) for point 1, (1.02L, 1.02L) for point 2, and (2.02L, 2.02L) for point 3. At point 1, which is situated between the fixed boundary and the circular hole, the displacement shows the complex pattern of multiple reflections. The deviation of the LBM simulations from the FEM is relatively low and only slightly increases with time. The points 2 and 3 are located further away from the hole on the diagonal from the lower left to the upper right corner of the domain. Thus, the wave takes longer to reach these points. The wave speed \(c_s\) can be evaluated by regarding the time it takes the wave to travel between two points. At point 2 the zero-crossing of the initial wave occurs at \({\hat{t}}^{(2)}_{\text {zero}} = 4.7\), whereas it occurs at \({\hat{t}}^{(3)}_{\text {zero}} = 6.1\) at point 3. The distance between these points is \(\sqrt{2}L\). The wave with wave speed cover this distance in a time of \(\sqrt{2} \, \nicefrac {L}{c_s}\), which is close to the observed time difference of \(1.4 \, \nicefrac {L}{c_s}\). The displacement in Fig. 13 shows a similar pattern for both points 2 and 3, shifted relative to each other due to the difference in traveling times of the respective waves. Larger peaks occur compared to point 1 due to constructive interference. With increasing time the absolute deviation becomes more prominent. The peaks of the FEM curve occur slightly earlier than in the LBM, and both implementations also increasingly deviate from each other as time increases. Furthermore, the LBM shows less distinctive peaks. Features, such as local minima and maxima that are rather close together, appear to be somewhat equalized, e.g., for point 2 around \({\hat{t}} = 9\). These variations in the LBM results account for the relatively high absolute deviation that occurs coinciding with peaks in the displacement.

However, there is generally good agreement between the results of both LBM implementations and the FEM results, despite the fundamentally different approaches. The example suggests that the LBM is suitable for elastodynamical problems such as wave propagation even with more complex geometries.

6 Conclusion

This work proposes two new approaches to treat boundary conditions in a lattice Boltzmann method (LBM) for the wave equation. To be specific, the LBM presented in [5] is considered. The new strategies allow treating boundaries that do not conform with the regular lattice, which allows the flexibility to model more complex domains even with a regular lattice that is typical for the LBM. This is particularly useful if the wave equation is considered as an idealization that describes the evolution of a displacement of a solid which is the case if the motion of a solid is limited to antiplane shear deformation. By means of a non-lattice-conforming treatment of boundary conditions, it is straightforward to model cracks which had to be implemented as notches of finite width in our previous work [17].

The first implementation of non-lattice-conforming boundary conditions relies on a more macroscopic view of boundary conditions. The goal here is to determine the distribution functions at the boundary such that this results in a prescribed value of the macroscopic field, for Dirichlet-type boundary conditions, or a macroscopically observable gradient, for Neumann-type boundary conditions. This algorithm involves the solution of a system of linear equations. Although the resulting system of linear equations is relatively small, this approach couples the algorithmic treatment of all boundary lattice points in every time step and thus may hinder parallelization of the overall LBM.

The second implementation of non-lattice-conforming boundary conditions is only able to implement Neumann boundary conditions, but allows to handle the boundary conditions for each boundary lattice point separately. This is a major advantage if one considers parallel implementations of the LBM. The idea is to derive the missing distribution functions at boundary lattice points from a balance of momentum for cells surrounding each boundary lattice point.

In two numerical experiments, the capabilities of both strategies are demonstrated. The first experiment considers a dynamically loaded stationary crack under antiplane shear assumptions. This problem already served as a benchmark in [17], and it is demonstrated that both new strategies notably improve the LBM results. Furthermore, both implementations outperform the FEM in terms of accuracy and computational efficiency, i.e., reduced runtime.

The second numerical example also illustrates how the new strategies are able to model geometries that do not conform to the strictly regular mesh employed in the LBM. Here, FEM simulations serve as a benchmark and the LBM simulations again agree well with the FEM results.