Frictional contact problem of one-dimensional hexagonal piezoelectric quasicrystals layer

Abstract

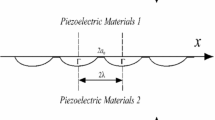
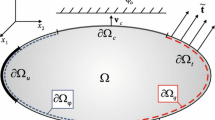
Based on three-dimensional (3D) general solutions for one-dimensional (1D) hexagonal piezoelectric quasicrystals (PEQCs), this paper studied the frictional contact problem of 1D hexagonal PEQCs layer. The frequency response functions for 1D hexagonal PEQCs layer are analytically derived by applying double Fourier integral transforms to the general solutions and boundary conditions, which are consequently converted to the corresponding influence coefficients. The conjugate gradient method is used to obtain the unknown pressure distribution, while the discrete convolution–fast Fourier transform technique is applied to calculate the displacements and stresses of phonon and phason, electric potentials and electric displacements. Numerical results are given to reveal the influences of layer thickness, material parameters and loading conditions on the contact behavior. The obtained 3D contact solutions are not only helpful for further analysis and understanding of the coupling characteristics of phonon, phason and electric field, but also provide a reference basis for experimental analysis and material development.

Appendices

Appendix A

The constants $a$,$b$,$c$,$d$ and $e$ involved in Eqs. (5, 6) are listed as follows:

$$\begin{aligned} & a = {C_{44}}[{\xi _{33}}(R_2^2 - {C_{33}}{K_1}) - {C_{33}}e_{33}^{\prime 2} - {K_1}e_{33}^2 + 2{R_2}{e_{33}}{e^\prime }_{33}] \\ & b = {\xi _{11}}{C_{44}}(R_2^2 - {C_{33}}{K_1}) - {\xi _{33}}[{C_{11}}{C_{33}}{K_1} + {C_{11}}R_2^2 + C_{13}^2{K_1} + 2{C_{13}}{C_{44}}{K_1} - 2{C_{13}}{R_2}({R_1} + {R_3}) - {C_{33}}{C_{44}}{K_2} \\ & + {C_{33}}{({R_1} + {R_3})^2} - 2{C_{44}}{R_1}{R_2}] - {C_{11}}({C_{33}}e_{33}^{\prime 2} + {R_1}e_{33}^2 - 2{R_2}{e_{33}}{e^\prime }_{33}) + {C_{13}}e_{33}^{\prime \prime 2}({C_{13}} + 2{C_{44}}) + 2{C_{13}}{K_1}{e_{33}}({e_{15}} \\ & + {e_{31}}) - 2{C_{13}}{e^\prime }_{33}[({R_1} + {R_3}){e_{33}} + {R_2}({e_{15}} + {e_{31}})] - {C_{33}}{K_1}{({e_{15}} + {e_{31}})^2} + 2{C_{33}}{e^\prime }_{33}[({R_1} + {R_3})({e_{15}} + {e_{31}}) - {C_{44}}{e^\prime }_{15}] \\ & - {C_{44}}{K_2}e_{33}^2 + 2{C_{44}}({K_1}{e_{31}}{e_{33}} - {R_1}{e_{33}}{e^\prime }_{33} - {R_2}{e_{31}}{e^\prime }_{33} + {R_2}{e_{33}}{e^\prime }_{15}) + {[{R_2}({e_{15}} + {e_{31}}) + {e_{33}}({R_1} + {R_3})]^2} \\ & c = {\xi _{11}}{C_{11}}(R_2^2 - {C_{33}}{K_1}) + {\xi _{11}}{C_{13}}{K_1}({C_{13}} + 2{C_{44}}) - 2{\xi _{11}}{C_{13}}{R_2}({R_1} + {R_3}) + {\xi _{11}}{C_{33}}(R_1^2 - {C_{44}}{K_2}) \\ & + {\xi _{11}}{C_{33}}{R_3}(2{R_1} + {R_3}) - 2{\xi _{11}}{C_{44}}{R_1}{R_2} - {\xi _{33}}{C_{11}}({C_{33}}{K_2} + {C_{44}}{K_1} - 2{R_2}{R_3}) + {\xi _{33}}{C_{13}}({C_{13}}{K_2} + 2{C_{44}}{K_2} \\ & - 2{R_1}{R_3} - 2R_3^2) + {\xi _{33}}{C_{44}}R_1^2 - {C_{11}}(2{C_{33}}{e^\prime }_{15}{e^\prime }_{33} + {C_{44}}e_{33}^{\prime 2} + 2{K_1}{e_{15}}{e_{33}} + {K_2}e_{33}^2) + 2{C_{11}}{R_2}({e_{15}}{e^\prime }_{33} + {e_{33}}{e^\prime }_{15}) \\ & + 2{e^\prime }_{33}[{C_{11}}{R_3}{e_{33}} + {e^\prime }_{15}(C_{13}^2 + 2{C_{13}}{C_{44}})] + 2{C_{13}}({K_1}{e_{15}} + {K_2}{e_{33}})({e_{15}} + {e_{31}}) - 2{C_{13}}{R_1}({e_{15}}{e^\prime }_{33} + {e_{33}}{e^\prime }_{15}) \\ & - 2{C_{13}}{R_2}{e^\prime }_{15}({e_{15}} + {e_{31}}) - 2{C_{13}}{R_3}(2{e_{15}}{e^\prime }_{33} + {e_{31}}{e^\prime }_{33} + {e_{33}}{e^\prime }_{15}) - {C_{33}}{C_{44}}e_{15}^{\prime 2} - {C_{33}}{K_2}{({e_{15}} + {e_{31}})^2} \\ & + 2{C_{33}}{R_1}{e^\prime }_{15}({e_{15}} + {e_{31}}) + 2{C_{33}}{R_3}{e^\prime }_{15}({e_{15}} + {e_{31}}) - {C_{44}}{K_1}e_{31}^2 + 2{C_{44}}{e_{31}}({K_2}{e_{33}} + {R_1}{e^\prime }_{33}) - 2{C_{44}}{e^\prime }_{15}({R_1}{e_{33}} \\ & + {R_2}{e_{31}}) + 2R_1^2{e_{15}}{e_{33}} - 2{R_1}{R_2}{e_{15}}({e_{15}} + {e_{31}}) + 2{R_1}{R_3}{e_{15}}{e_{33}} - 2{R_3}{e_{31}}[({R_1} + {R_3}){e_{33}} - {R_2}({e_{15}} + {e_{31}})] \\ & d = - {\xi _{11}}{C_{11}}({C_{33}}{K_2} + {C_{44}}{K_1} - 2{R_2}{R_3}) + {\xi _{11}}C_{13}^2{K_2} + 2{\xi _{11}}{C_{13}}({C_{44}}{K_2} - {R_1}{R_3} - R_3^2) + {\xi _{11}}{C_{44}}R_1^2 \\ & - {\xi _{33}}{C_{11}}({C_{44}}{K_2} - R_3^2) - {C_{11}}({C_{33}}e_{15}^{\prime 2} + 2{C_{44}}{e^\prime }_{15}{e^\prime }_{33} + {K_1}e_{15}^2) - 2{C_{11}}{e_{15}}({K_2}{e_{33}} - {R_2}{e^\prime }_{15} - {R_3}{e^\prime }_{33}) \\ & + 2{C_{11}}{R_3}{e_{33}}{e^\prime }_{15} + C_{13}^2e_{15}^{\prime 2} + 2{C_{13}}{C_{44}}e_{15}^{\prime 2} + 2{C_{13}}{K_2}{e_{15}}({e_{15}} + {e_{31}}) - 2{C_{13}}{R_1}{e_{15}}{e^\prime }_{15} \\ & - 2{C_{13}}{R_3}{e^\prime }_{15}(2{e_{15}} + {e_{31}}) - {C_{44}}{K_2}e_{31}^2 + 2{R_1}{e_{31}}({C_{44}}{e^\prime }_{15} - {R_3}{e_{15}}) + R_1^2e_{15}^2 + R_3^2e_{31}^2 \\ & e = {C_{11}}(R_3^2 - {C_{44}}{K_2} - {C_{44}}e_{15}^{\prime 2} - {K_2}e_{15}^2 + 2{R_3}{e_{15}}{e^\prime }_{15}) \\ \end{aligned}$$

(23)

The constants $a_{i} ,b_{i} ,c_{i}$ and $d_{i}$ involved in Eqs. (5, 6) are listed as follows:

$$\begin{aligned} a_{1} & = - \xi _{{33}} (C_{{13}} K_{1} + C_{{44}} K_{1} - R_{1} R_{2} - R_{2} R_{3} ) - (C_{{13}} + C_{{44}} )e_{{33}}^{{\prime 2}} - K_{1} e_{{33}} (e_{{15}} + e_{{31}} ) + [(R_{1} + R_{3} )e_{{33}} + R_{2} (e_{{15}} + e_{{31}} )]e^{\prime } _{{33}} \\ b_{1} & = - \xi _{{11}} [(C_{{13}} + C_{{44}} )K_{1} - (R_{1} + R_{3} )R_{2} )] - \xi _{{33}} [(C_{{13}} + C_{{44}} )K_{2} - R_{1} R_{3} - R_{3}^{2} )] - 2e^{\prime } _{{15}} e^{\prime } _{{33}} (C_{{13}} + C_{{44}} ) \\ & \quad - (K_{1} e_{{15}} + K_{2} e_{{33}} )(e_{{15}} + e_{{31}} ) + R_{1} (e_{{15}} e^{\prime } _{{33}} + e_{{33}} e^{\prime } _{{15}} ) + R_{2} e^{\prime } _{{15}} (e_{{15}} + e_{{31}} ) + R_{3} (2e_{{15}} e^{\prime } _{{33}} + e_{{31}} e^{\prime } _{{33}} + e_{{33}} e^{\prime } _{{15}} ) \\ c_{1} & = - \xi _{{11}} [(C_{{13}} + C_{{44}} )K_{2} - (R_{1} + R_{3} )R_{3} ] - (C_{{13}} + C_{{44}} )e_{{15}}^{{\prime 2}} - K_{2} e_{{15}} (e_{{15}} + e_{{31}} ) + (R_{1} e_{{15}} + 2R_{3} e_{{15}} + R_{3} e_{{31}} )e^{\prime } _{{15}} \\ a_{2} & = - C_{{44}} (\xi _{{33}} K_{1} + e_{{33}}^{{\prime 2}} ) \\ b_{2} & = \xi _{{33}} [(R_{1} + R_{3} )^{2} - C_{{11}} K_{1} - C_{{44}} K_{2} ] - C_{{11}} e_{{33}}^{{\prime 2}} - C_{{44}} (\xi _{{11}} K_{1} + 2e^{\prime } _{{15}} e^{\prime } _{{33}} ) - K_{1} (e_{{15}} + e_{{31}} )^{2} \\ & \quad + 2e^{\prime } _{{33}} (e_{{15}} + e_{{31}} )(R_{1} + R_{3} ) \\ c_{2} & = \xi _{{11}} [(R_{1} + R_{3} )^{2} - C_{{11}} K_{1} - C_{{44}} K_{2} )] - C_{{44}} e_{{15}}^{{\prime 2}} - C_{{11}} (\xi _{{33}} K_{2} + 2e^{'} _{{15}} e^{'} _{{33}} ) - K_{2} (e_{{15}} + e_{{31}} )^{2} \\ & \quad + 2e^{'} _{{15}} (e_{{15}} + e_{{31}} )(R_{1} + R_{3} ) \\ d_{2} & = - C_{{11}} (\xi _{{11}} K_{2} + e_{{15}}^{{'2}} ) \\ a_{3} & = C_{{44}} (\xi _{{33}} R_{2} + e_{{33}} e^{'} _{{33}} ) \\ b_{3} & = \xi _{{11}} C_{{44}} R_{2} + \xi _{{33}} (C_{{11}} R_{2} - C_{{13}} R_{1} - C_{{13}} R_{3} - C_{{44}} R_{1} ) + C_{{11}} e_{{33}} e^{'} _{{33}} \\ & \quad - (C_{{13}} e^{'} _{{33}} + R_{1} e_{{33}} )(e_{{15}} + e_{{31}} ) - C_{{44}} (e_{{31}} e^{'} _{{33}} - e_{{33}} e^{'} _{{15}} ) + R_{2} (e_{{15}} + e_{{31}} )^{2} - R_{3} e_{{33}} (e_{{15}} + e_{{31}} ) \\ c_{3} & = \xi _{{11}} [C_{{11}} R_{2} - C_{{13}} (R_{1} + R_{3} ) - C_{{44}} R_{1} ] + C_{{11}} (\xi _{{33}} R_{3} + e_{{15}} e^{'} _{{33}} + e_{{33}} e^{'} _{{15}} ) \\ & \quad - C_{{13}} e^{'} _{{15}} (e_{{15}} + e_{{31}} ) - C_{{44}} e_{{31}} e^{'} _{{15}} - R_{1} e_{{15}}^{2} - (R_{1} - R_{3} )e_{{15}} e_{{31}} + R_{3} e_{{31}}^{2} \\ d_{3} & = C_{{11}} (\xi _{{11}} R_{3} + e_{{15}} e^{'} _{{15}} ) \\ a_{4} & = C_{{44}} (R_{2} e^{'} _{{33}} - K_{1} e_{{33}} ) \\ b_{4} & = C_{{11}} (R_{2} e^{'} _{{33}} - K_{1} e_{{33}} ) + C_{{13}} K_{1} (e_{{15}} + e_{{31}} ) - C_{{13}} e^{'} _{{33}} (R_{1} + R_{3} ) + C_{{44}} (K_{1} e_{{31}} - K_{2} e_{{33}} - R_{1} e^{'} _{{33}} + R_{2} e^{'} _{{15}} ) \\ & \quad - R_{2} (e_{{15}} + e_{{31}} )(R_{1} + R_{3} ) + (R_{1} + R_{3} )^{2} e_{{33}} \\ c_{4} & = C_{{11}} (R_{2} e^{'} _{{15}} + R_{3} e^{'} _{{33}} - K_{1} e_{{15}} - K_{2} e_{{33}} ) + C_{{13}} K_{2} (e_{{15}} + e_{{31}} ) - C_{{13}} e^{'} _{{15}} (R_{1} + R_{3} ) \\ & \quad + C_{{44}} (K_{2} e_{{31}} - R_{1} e^{'} _{{15}} ) + R_{1}^{2} e_{{15}} + R_{1} R_{3} (e_{{15}} - e_{{31}} ) - R_{3}^{2} e_{{31}} \\ d_{4} & = C_{{11}} (R_{3} e^{'} _{{15}} - K_{2} e_{{15}} ) \\ \end{aligned}$$

(24)

In order to define the constants in Eq. (7), the following auxiliary constants $\lambda_{ki}$, $\gamma_{ki}$ and $\rho_{i}$ are introduced as:

$$\begin{aligned} \gamma_{0i} & = s_{i} (C_{13} \alpha_{1i} + R_{1} \alpha_{2i} + e_{31} \alpha_{3i} ) - C_{11} \\ \gamma_{1i} & = s_{i} (C_{33} \alpha_{1i} + R_{2} \alpha_{2i} + e_{33} \alpha_{3i} ) - C_{13} \\ \gamma_{2i} & = s_{i} (R_{2} \alpha_{1i} + K_{1} \alpha_{2i} + e_{33}^{{\prime }} \alpha_{3i} ) - R_{1} \\ \gamma_{3i} & = s_{i} (e_{33} \alpha_{1i} + e_{33}^{{\prime }} \alpha_{2i} + \xi_{33} \alpha_{3i} ) - e_{31} \\ \lambda_{1i} & = C_{44} (\alpha_{1i} + s_{i} ) + R_{3} \alpha_{2i} + e_{15} \alpha_{3i} \\ \lambda_{2i} & = R_{3} (\alpha_{1i} + s_{i} ) + K_{2} \alpha_{2i} + e_{15}^{{\prime }} \alpha_{3i} \\ \lambda_{3i} & = e_{15} (\alpha_{1i} + s_{i} ) + e_{15}^{{\prime }} \alpha_{2i} - \xi_{11} \alpha_{3i} \\ \rho_{1} & = C_{44} ,\rho_{2} = R_{3} ,\rho_{3} = e_{15}. \\ \end{aligned}$$

(25)

Appendix B

The intermediate variables $p_{1} ,q_{1} ,t_{ki}^{(n)} ,a_{ki}^{(n)}$ and $\overline{t}_{ki}^{(n)} ,\overline{a}_{ki}^{(n)}$ in Eq. (14) are:

$$\begin{aligned} t_{0i} & = - \gamma_{0i} - \gamma_{04} e^{{ - \alpha (s_{i} + s_{4} )h}} \quad (i = 1 - 4),\overline{t}_{0i} = \gamma_{0i} - \gamma_{04} e^{{\alpha (s_{i} - s_{4} )h}} \quad (i = 1 - 3) \\ t_{ki} & = \gamma_{ki} - \gamma_{k4} e^{{ - \alpha (s_{i} + s_{4} )h}} \quad (k = 1 - 3,i = 1 - 4),\overline{t}_{ki} = \gamma_{ki} - \gamma_{k4} e^{{\alpha (s_{i} - s_{4} )h}} \quad (k = 1 - 3,i = 1 - 3) \\ a_{ki} & = (\alpha_{ki} + \alpha_{k4} )e^{{ - \alpha s_{i} h}} \quad (k = 1 - 3,i = 1 - 4),\overline{a}_{ki} = ( - \alpha_{ki} + \alpha_{k4} )e^{{\alpha s_{i} h}} \quad (k = 1 - 3,i = 1 - 3) \\ t_{ki}^{(1)} & = t_{ki} - {{\overline{t}_{k3} a_{3i} } \mathord{\left/ {\vphantom {{\overline{t}_{k3} a_{3i} } {\overline{a}_{33} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{33} }}\quad (k = 0 - 3,i = 1 - 4),\overline{t}_{ki}^{(1)} = \overline{t}_{ki} - {{\overline{t}_{k3} \overline{a}_{3i} } \mathord{\left/ {\vphantom {{\overline{t}_{k3} \overline{a}_{3i} } {\overline{a}_{33} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{33} }}\quad (k = 0 - 2,i = 1,2) \\ a_{ki}^{(1)} & = a_{ki} - {{\overline{a}_{k3} a_{3i} } \mathord{\left/ {\vphantom {{\overline{a}_{k3} a_{3i} } {\overline{a}_{33} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{33} }}\quad (k = 1,2,i = 1 - 4),\overline{a}_{ki}^{(1)} = \overline{a}_{ki} - {{\overline{a}_{k3} \overline{a}_{3i} } \mathord{\left/ {\vphantom {{\overline{a}_{k3} \overline{a}_{3i} } {\overline{a}_{33} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{33} }}\quad (k = 1,2,i = 1,2) \\ t_{ki}^{(2)} & = t_{ki}^{(1)} - {{\overline{t}_{k2}^{(1)} a_{2i}^{(1)} } \mathord{\left/ {\vphantom {{\overline{t}_{k2}^{(1)} a_{2i}^{(1)} } {\overline{a}_{22}^{(1)} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{22}^{(1)} }}\quad (k = 0 - 3,i = 1 - 4),\overline{t}_{k1}^{(2)} = \overline{t}_{k1}^{(1)} - {{\overline{t}_{k2} \overline{a}_{21}^{(1)} } \mathord{\left/ {\vphantom {{\overline{t}_{k2} \overline{a}_{21}^{(1)} } {\overline{a}_{22}^{(1)} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{22}^{(1)} }}\quad (k = 0 - 3) \\ a_{1i}^{(2)} & = a_{1i}^{(1)} - {{\overline{a}_{12}^{(1)} a_{21}^{(1)} } \mathord{\left/ {\vphantom {{\overline{a}_{12}^{(1)} a_{21}^{(1)} } {\overline{a}_{22}^{(1)} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{22}^{(1)} }}(i = 1 - 4),\overline{a}_{11}^{(2)} = \overline{a}_{11}^{(1)} - {{\overline{a}_{12}^{(1)} \overline{a}_{21}^{(1)} } \mathord{\left/ {\vphantom {{\overline{a}_{12}^{(1)} \overline{a}_{21}^{(1)} } {\overline{a}_{22}^{(1)} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{22}^{(1)} }} \\ t_{ki}^{(3)} & = t_{ki}^{(2)} - {{\overline{t}_{k1}^{(2)} a_{1i}^{(2)} } \mathord{\left/ {\vphantom {{\overline{t}_{k1}^{(2)} a_{1i}^{(2)} } {\overline{a}_{11}^{(2)} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{11}^{(2)} }}\quad (k = 0 - 3,i = 1 - 4) \\ t_{ki}^{(4)} & = t_{ki}^{(3)} - {{t_{k4}^{(3)} t_{3i}^{(3)} } \mathord{\left/ {\vphantom {{t_{k4}^{(3)} t_{3i}^{(3)} } {t_{34}^{(3)} }}} \right. \kern-\nulldelimiterspace} {t_{34}^{(3)} }}\quad (k = 0 - 2,i = 1 - 3) \\ t_{ki}^{(5)} & = t_{ki}^{(4)} - {{t_{k3}^{(4)} t_{2i}^{(4)} } \mathord{\left/ {\vphantom {{t_{k3}^{(4)} t_{2i}^{(4)} } {t_{23}^{(4)} }}} \right. \kern-\nulldelimiterspace} {t_{23}^{(4)} }}\quad (k = 0,1,i = 1,2) \\ t_{01}^{(6)} & = t_{01}^{(5)} - {{t_{02}^{(5)} t_{11}^{(5)} } \mathord{\left/ {\vphantom {{t_{02}^{(5)} t_{11}^{(5)} } {t_{12}^{(5)} }}} \right. \kern-\nulldelimiterspace} {t_{12}^{(5)} }} \\ p_{1} & = {{\tilde{\tilde{p}}_{z} } \mathord{\left/ {\vphantom {{\tilde{\tilde{p}}_{z} } {\alpha^{2} }}} \right. \kern-\nulldelimiterspace} {\alpha^{2} }} - {{\tilde{\tilde{q}}_{z} t_{14}^{(3)} } \mathord{\left/ {\vphantom {{\tilde{\tilde{q}}_{z} t_{14}^{(3)} } {(t_{34}^{(3)} \alpha^{2} }}} \right. \kern-\nulldelimiterspace} {(t_{34}^{(3)} \alpha^{2} }}) - {{q_{1} t_{13}^{(4)} } \mathord{\left/ {\vphantom {{q_{1} t_{13}^{(4)} } {t_{23}^{(4)} }}} \right. \kern-\nulldelimiterspace} {t_{23}^{(4)} }},q_{1} = {{\tilde{\tilde{h}}_{z} } \mathord{\left/ {\vphantom {{\tilde{\tilde{h}}_{z} } {\alpha^{2} }}} \right. \kern-\nulldelimiterspace} {\alpha^{2} }} - {{\tilde{\tilde{q}}_{z} t_{24}^{(3)} } \mathord{\left/ {\vphantom {{\tilde{\tilde{q}}_{z} t_{24}^{(3)} } {(t_{34}^{(3)} \alpha^{2} )}}} \right. \kern-\nulldelimiterspace} {(t_{34}^{(3)} \alpha^{2} )}}. \\ \end{aligned}$$

(26)