Skip to main content
SpringerLink
Log in

Exact solution for bending analysis of two-directional functionally graded Timoshenko beams

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

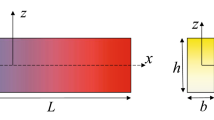
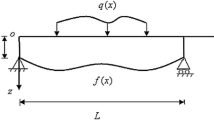
This paper studies the bending behavior of two-dimensional functionally graded (TDFG) beam based on the Timoshenko beam theory, where the material properties of the beam vary both in the length and thickness directions. By introducing a new auxiliary function, we simplify the coupled governing equations for the deflection and rotation to a single governing equation. Moreover, all physical quantities of interest can be expressed in terms of the auxiliary function. Then, the exact analytical solutions for bending of TDFG Timoshenko beams are derived for various boundary conditions. The influence of gradient indexes on the deflection and stress distribution of TDFG Timoshenko beams is discussed subjected to different transverse loadings, including uniformly distributed loading, linearly distributed loading and concentrated external loading. The introduced approach is of benefit to exact bending analysis of TDFG beams by employing other beam theories.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Birman, V., Byrd, L.W.: Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 60, 195–216 (2007)

    Article  Google Scholar 

  2. Sankar, B.V.: An elasticity solution for functionally graded beams. Compos. Sci. Technol. 61, 689–696 (2001)

    Article  Google Scholar 

  3. Kadoli, R., Akhtar, K., Ganesan, N.: Static analysis of functionally graded beams using higher order shear deformation theory. Appl. Math. Model. 32, 2509–2525 (2008)

    Article  Google Scholar 

  4. Li, X.F.: A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler–Bernoulli beams. J. Sound Vib. 318, 1210–1229 (2008)

    Article  Google Scholar 

  5. Thai, H.T., Vo, T.P.: Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. Int. J. Mech. Sci. 62, 57–66 (2012)

    Article  Google Scholar 

  6. Yang, Q., Zheng, B.L., Zhang, K., Li, J.: Elastic solutions of a functionally graded cantilever beam with different modulus in tension and compression under bending loads. Appl. Math. Model. 38, 1403–1416 (2014)

    Article  MathSciNet  Google Scholar 

  7. Hadji, L., Daouadji, T.H., Tounsi, A., et al.: A n-order refined theory for bending and free vibration of functionally graded beams. Struct. Eng. Mech. 54, 923–936 (2015)

    Article  Google Scholar 

  8. Li, X.B., Li, L., Hu, Y.J.: Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos. Struct. 165, 250–265 (2017)

    Article  Google Scholar 

  9. Elishakoff, I., Kaplunov, J., Nolde, E.: Celebrating the centenary of Timoshenko’s study of effects of shear deformation and rotary inertia. Appl. Mech. Rev. 67, 060802 (2015)

    Article  Google Scholar 

  10. Viet, N.V., Zaki, W., Umer, R.: Analytical model of functionally graded material/shape memory alloy composite cantilever beam under bending. Compos. Struct. 203, 764–776 (2018)

    Article  Google Scholar 

  11. Nemat-Alla, M.: Reduction of thermal stresses by developing two-dimensional functionally graded materials. Int. J. Solid Struct. 40, 7339–7356 (2003)

    Article  Google Scholar 

  12. Pydah, A., Sabale, A.: Static analysis of bi-directional functionally graded curved beams. Compos. Struct. 160, 867–876 (2017)

    Article  Google Scholar 

  13. Lu, C.F., Chen, W.Q., Xu, R.Q., Lim, C.W.: Semi-analytical elasticity solutions for bi-directional functionally graded beams. Int. J. Solid Struct. 45, 258–275 (2008)

    Article  Google Scholar 

  14. Simsek, M.: Bi-directional functionally graded materials (BDFGMs) for free and forced vibration of Timoshenko beams with various boundary conditions. Compos. Struct. 133, 968–978 (2015)

    Article  Google Scholar 

  15. Simsek, M.: Buckling of Timoshenko beams composed of two-dimensional functionally graded material (2D-FGM) having different boundary conditions. Compos. Struct. 149, 304–314 (2016)

    Article  Google Scholar 

  16. Huynh, T.A., Lieu, X.Q., Lee, J.: NURBS-based modeling of bidirectional functionally graded Timoshenko beams for free vibration problem. Compos. Struct. 160, 1178–1190 (2017)

    Article  Google Scholar 

  17. Nguyen, D.K., Nguyen, Q.H., Tran, T.T., Bui, V.T.: Vibration of bi-dimensional functionally graded Timoshenko beams excited by a moving load. Acta Mech. 228, 141–155 (2017)

    Article  MathSciNet  Google Scholar 

  18. Karamanli, A.: Free vibration analysis of two directional functionally graded beams using a third order shear deformation theory. Compos. Struct. 189, 127–136 (2018)

    Article  Google Scholar 

  19. Tang, Y., Lv, X.F., Yang, T.Z.: Bi-directional functionally graded beams: asymmetric modes and nonlinear free vibration. Compos. Part B 156, 319–331 (2019)

    Article  Google Scholar 

  20. Fariborz, J., Batra, R.C.: Free vibration of bi-directional functionally graded material circular beams using shear deformation theory employing logarithmic function of radius. Compos. Struct. 210, 217–230 (2019)

    Article  Google Scholar 

  21. Chen, X.C., Zhang, X.L., Lu, Y.X., Li, Y.H.: Static and dynamic analysis of the postbuckling of bi-directional functionally graded material microbeams. Int. J. Mech. Sci. 151, 424–443 (2019)

    Article  Google Scholar 

  22. Zhao, L., Zhu, J., Wen, X.D.: Exact analysis of bi-directional functionally graded beams with arbitrary boundary conditions via the symplectic approach. Struct. Eng. Mech. 59, 101–122 (2016)

    Article  Google Scholar 

  23. Pydah, A., Sabale, A.: Static analysis of bi-directional functionally graded curved beams. Compos. Struct. 160, 867–876 (2017)

    Article  Google Scholar 

  24. Karamanli, A.: Elastostatic analysis of two-directional functionally graded beams using various beam theories and Symmetric Smoothed Particle Hydrodynamics method. Compos. Struct. 160, 653–669 (2017)

    Article  Google Scholar 

  25. Li, J., Guan, Y.J., Wang, G.C., et al.: Meshless modeling of bending behavior of bi-directional functionally graded beam structures. Compos. Part B 155, 104–111 (2018)

    Article  Google Scholar 

  26. Elishakoff, I.: Handbook on Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate Theories. World Scientific, Singapore (2019)

    Book  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the reviewers for their valuable suggestions to improve the quality of the paper. This work was supported by Natural Science Foundation of Guangdong Province, PR China (Grant No. 2018A030313258).

Author information

Authors and Affiliations

  1. School of Mathematics and Big Data, Foshan University, Foshan, 528000, Guangdong, China

    Yong Huang & Zheng-Yong Ouyang

Authors
  1. Yong Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zheng-Yong Ouyang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yong Huang.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, Y., Ouyang, ZY. Exact solution for bending analysis of two-directional functionally graded Timoshenko beams. Arch Appl Mech 90, 1005–1023 (2020). https://doi.org/10.1007/s00419-019-01655-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-019-01655-5

Keywords

Search

Navigation