1 Introduction

It is well known that in many mechanical engineering systems, a contact between individual elements is not continuous. This may be an intended effect or a result of gradual destruction of the mechanical parts. Regardless of the cause, the collisions between various elements entail significant increase in the dynamic loads what leads to the greater destruction of the colliding elements.

In many papers dealing with collisions in multi-body systems consisting of rigid bodies, the influence of friction forces on the kinematic state of the bodies after impact is omitted. An approach to three-dimensional analysis of the collision of rigid bodies with friction was originally formulated by Routh [1]. In recent years, many researchers rediscover the Routh model [2], analyzing it in detail [4] and also applying it in modeling of relatively simple problems concerning collisions of free bodies [5] as well as collisions in the multi-body systems with impacts [6]. On the base of Routh’s model, some more advanced models have been recently developed [3, 7, 8].

In this paper, the collisions between a double pendulum and a motionless obstacle having a rough surface are investigated. The friction forces accompanying the collision are taken into account, and the Routh model is employed in order to modeling the single collision. This paper is continuation of paper [6]. Mathematical model of the motion of the pendulum which many times collides with the obstacle has been extended here, particularly with regard to the idea of modeling as a piecewise smooth system. Moreover, the exact formulas for coefficients of line of sticking and line of maximum compression which are unique for the considered multi-body system are presented in the paper. Simulations illustrating the application of the proposed model have been carried out to demonstrate the influence of friction forces on the collision what, in effect, has a significant impact on the pendulum behavior in longer time.

2 Model of the system

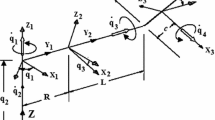
The behavior of a double pendulum colliding with an obstacle is considered (see Fig. 1a). The system is constrained to move in a fixed vertical plane. The pendulum, suspended at the point O, consists of two rigid bodies linked by a joint A. One of the bodies is a rod of mass \(m_{1}\) and length \(l_{1}\). The second part of the pendulum is composed of a rod of length \(l_{2}\) and a disk of radius r. The rod and the disk are connected to each other in a rigid manner. Their common mass is equal \(m_{2}\). \(C_{1}\) and \(C_{2}\) are the mass centers of the both parts. \(I_{1}\) and \(I_{2}\) denote the moments of inertia of the parts with respect to the axes which pass through the points \(C_{1}\) and \(C_{2}\), respectively, and are perpendicular to the plane of motion. There is viscous damping at the both joints with a priori known coefficients \(c_{1}\) and \(c_{2}\). Moreover, two torques \(M_{1}(t) = M_{01} \cos (\Omega _{1}t)\) and \(M_{2}(t) = M_{02} \cos (\Omega _{2}t)\) are taken into consideration.

Fig. 1
figure 1

a Double pendulum colliding with a rough surface. b Generalized coordinates

Full size image

The angles \(\psi _{1}\) and \(\psi _{2}\) are chosen as the general coordinates. The obstacle is motionless, and its surface is plane and rough. We assume that the distance D between the obstacle and the point O fulfills the following conditions

$$\begin{aligned} l_1<D<l_1 +l_2 +2r. \end{aligned}$$
(1)

So, the motion of the pendulum is constrained by unilateral constraint of the form

$$\begin{aligned} D-l_1 \cos (\psi _1 )-(l_2 +r)\cos (\psi _2 ) -r\ge 0, \end{aligned}$$
(2)

and only the disk placed at the end of the pendulum may come into contact with the rough obstacle.

3 Mathematical model

Observe that the unilateral constraint (2) does not act in relatively long intervals. From the point of view of the slow time scale which is suitable to observe the pendulum motion, it becomes active only in some time instants. When the contact with the obstacle occurs, the pendulum exhibits discontinuous behavior. The velocities of the both pendulum parts as well as the reaction forces at the joints and in the contact point with the obstacle undergo rapid changes. The pendulum, the motion of which is constrained by inequality (2), will be treated as piecewise smooth system. The main idea of such approach is presented in Fig. 2. On the right side, we can see the time line involving the whole process. On the time axis, the collisions are represented by several instants \(t_1^*,t_2^*,t_3^*,\ldots \). The motion starts from the known initial conditions at time \(t = 0\). All the intervals in which kinematic and dynamic quantities change continuously are separated from each other by the instants \(t_1^*,t_2^*,t_3^*,\ldots \) in which some of them change abruptly. The pendulum configuration given by \(\psi _1 (t_i^{*-} ), \psi _2 (t_i^{*-} )\) and its kinematic state \({\dot{\psi }}_1 (t_i^{*-} ), {\dot{\psi }}_2 (t_i^{*-} )\) just before the ith collision decides on the course of the collision. In turn, its kinematic state \({\dot{\psi }}_1 (t_i^{*+} ), {\dot{\psi }}_2 (t_i^{*+} )\) just after the ith collision determines the initial values for the next motion phase when the constraints (1) become inactive.

Fig. 2
figure 2

Double pendulum as a the piecewise smooth system

Full size image

3.1 Motion between collisions

In each relatively long term between the collisions, the pendulum motion is determined by differential equations and initial conditions. The equations of the double pendulum motion derived from the Lagrange equations of the second kind and written in matrix notation are as follows

$$\begin{aligned} \mathbf{A}\cdot {\varvec{{\ddot{\Psi }}}}=\mathbf{Q}, \end{aligned}$$
(3)

where

$$\begin{aligned} \mathbf{A}= & {} \left[ \begin{array}{lll} a_{11}&{}\quad a_{12} \\ a_{21}&{}\quad a_{22}\\ \end{array}\right] ,\quad {{\varvec{{\ddot{\Psi }}}}}=\left[ \begin{array}{lll} {{\ddot{\psi }}_1 } \\ {{\ddot{\psi }}_2 } \\ \end{array}\right] ,\quad \mathbf{Q}=\left[ \begin{array}{l} q_1 (t,\psi _1 ,\psi _2, {\dot{\psi }}_1 ,{\dot{\psi }}_2) \\ q_2 (t,\psi _1 ,\psi _2, {\dot{\psi }}_1 ,{\dot{\psi }}_2) \\ \end{array}\right] , \\ a_{11}= & {} I_1 +l_1^2 \left( {\frac{m_1}{4}+m_2}\right) ,\; a_{22} =I_2 +l_c^2 m_2,\quad a_{12} =a_{21} =l_1 l_c m_2 \cos (\psi _1 -\psi _2 ),\\ q_1= & {} M_{01} \cos (\Omega _1 t)-(c_1 +c_2 ){\dot{\psi }}_1 +c_2 {\dot{\psi }}_2 -l_1 l_c m_2 \sin (\psi _1 -\psi _2 ){\dot{\psi }}_2^2 -\left( {\frac{m_1}{2}+m_2}\right) gl_1 \sin \psi _1,\\ q_2= & {} M_{02}\cos (\Omega _2 t)+c_2({\dot{\psi }}_1 -{\dot{\psi }}_2 )+l_1 l_c m_2\sin (\psi _1-\psi _2){\dot{\psi }}_1^2 -m_2 gl_c \sin \psi _2,\\ l_c= & {} AC_2 . \end{aligned}$$

The configuration of the pendulum at time instant \(t_{i}\) and its kinematic state after ith collision are assumed as the initial values for the motion in (\(i+1\))th interval. Taking into account also the conditions at t = 0, we can write

$$\begin{aligned} {\varvec{\Psi }} (t_i )={\varvec{\Psi }}_{0i}, \quad {\varvec{{{\dot{\Psi }}}}}(t_i )={{\varvec{\Theta }}}_{0i}, \quad i=0, 1, 2,\ldots \end{aligned}$$
(4)

The vectors \({{\varvec{\Psi }}}_{00} ,{{\varvec{\Theta }}}_{00} \) are known a priori, while both the vectors \({{\varvec{\Psi }}}_{0i} ,{{\varvec{\Theta }} }_{0i} \) (for \(i>\) 0) are determined, using the Routh method, for each of the collision event.

Solving equation (3) with respect to the vector \({\varvec{{\ddot{\Psi }}}}\) we obtain

$$\begin{aligned} {{\varvec{{\ddot{\Psi }}}}}=\mathbf{A}^{-1}\cdot \mathbf{Q}, \end{aligned}$$
(5)

where \(\mathbf{A}^{-1}\) is the inverse matrix of \(\mathbf{A}\).

The determinant of the matrix A

$$\begin{aligned} \left| \mathbf{A} \right| =I_1 \left( I_2 +l_c^2 m_2 \right) +\frac{1}{4}l_1^2 \left( I_2 m_1 +4I_2 m_2 +l_c^2 m_1 m_2 \right) +l_1^2 l_c^2 m_2^2 \sin ^{2}\left( \psi _1 -\psi _2 \right) \end{aligned}$$
(6)

is positive for each pendulum configuration. Hence, the matrix A is regular.

Each of the initial value problems (5) with appropriate initial conditions (4) is solved numerically using the fourth order Runge–Kutta method. Usefulness of the method as well as the choice of the suitable time step h have been tested numerically.

3.2 Kinematic aspect of the collision

An important element of the algorithm used to solving the initial problem (4) and (5) is the continuous tracking of the pendulum position in order to detect the collision with the obstacle. Accordingly to inequality (2) we define the function f

$$\begin{aligned} f\left( \psi _1 (t),\psi _2 (t)\right) =D-l_1 \cos \left( \psi _1 (t)\right) -\left( l_2 +r\right) \cos \left( \psi _2 (t)\right) -r. \end{aligned}$$
(7)

The collision occurs exactly when

$$\begin{aligned} f\left( \psi _1 (t),\psi _2 (t)\right) =0. \end{aligned}$$
(8)

So, every time when function f changes its sign the Runge–Kutta algorithm is discontinued. Let us suppose that for some interval \(\langle {t{ }_j, t{ }_{j+1}} \rangle \), where \(t{ }_{j+1}= t{ }_j+ h\), the relationship

$$\begin{aligned} f(\psi _{1j} ,\psi _{2j} )f(\psi _{1 \left( {j+1} \right) } ,\psi _{2\left( {j+1} \right) } )<0 \end{aligned}$$
(9)

is true. \(\psi _{1j} , \psi _{2j} \) and \(\psi _{1 \left( {j+1} \right) } ,\;\psi _{2\left( {j+1} \right) } \) are approximate values of \(\psi _1 (t_j ), \psi _2 (t_j )\) and \(\psi _1 (t_{j+1} ), \psi _2 (t_{j+1} )\), respectively.

Fulfillment of the condition (9) means that in the found interval \(\left\langle {t{ }_j, t{ }_{j+1}} \right\rangle \) the collision appears. Let it be the ith collision event from the beginning of the movement. The function f is interpolated linearly in the found interval what allows to determine approximately the instant \(t_{{ }_i}^*\)

$$\begin{aligned} t_{{ }_i}^*\approx \frac{f(\psi _{1j} ,\psi _{2j} )(t_j +h)-f(\psi _{1 \left( {j+1} \right) } ,\psi _{2\left( {j+1} \right) } ) t_j }{f(\psi _{1j} ,\psi _{2j} )-f(\psi _{1 \left( {j+1} \right) } ,\psi _{2\left( {j+1} \right) } )}. \end{aligned}$$
(10)

The approximate values of both angles \(\psi _1 (t_i^{*-} ),\;\psi _2 (t_i^{*-} )\) as well as the angular velocities \({\dot{\psi }}_1 (t_i^{*-} ), {\dot{\psi }}_2 (t_i^{*-} )\) are calculated using the linear interpolation. For instance, the value approximating the value of the angle at the instant \(t_{{ }_i}^{*-} \) is assumed as follows

$$\begin{aligned} \psi _1 (t_{{ }_i}^{*-} )\approx \frac{\psi _{1 \left( {j+1} \right) } f(\psi _{1j} ,\psi _{2j} )-\psi _{1j} f(\psi _{1 \left( {j+1} \right) } ,\psi _{2\left( {j+1} \right) } ) }{f(\psi _{1j} ,\psi _{2j} )-f(\psi _{1 \left( {j+1} \right) } ,\psi _{2\left( {j+1} \right) } )}. \end{aligned}$$
(11)

The approximate values of \( \psi _2 (t_i^{*-} ), \;{\dot{\psi }}_1 (t_i^{*-} ), {\dot{\psi }}_2 (t_i^{*-} )\) are calculated in the same manner.

3.3 Collision laws

Modeling the collision, we assume commonly used assumptions. All displacements and rotations during the collision are negligible, therefore

$$\begin{aligned} \psi _1 (t_{{ }_i}^{*+} )=\psi _1 (t_{{ }_i}^{*-} ), \quad {\psi _2 (t_{{ }_i}^{*+} )=\psi _2 (t_{{ }_i}^{*-} )}, \quad i=1,2,\ldots \end{aligned}$$
(12)

The colliding bodies remain rigid and interact on each other only at one point. In time scale adapted for description of pendulum motion the duration of each collision is very short. However, during the collision the forces as well as the velocities and the accelerations change rapidly and these changes require to be described in a different time scale. We introduce the fast scale time \(\tau \) being more suitable for the collisions modeling. For each collision, the time \(\tau \) runs from 0 to \(\tau _{_i }^f \). The impulses of the contact forces at the contact point M as well as the forces at joints O and A are bounded when time \(\tau _{_i }^f \) tends to zero. The forces whose impulses are taken into account are shown in Fig. 3. The impulses of the gravity forces, the damping forces and both torques may be neglected due to very short duration of collision. The Cartesian coordinate system Mxyz depicted in Fig. 3 is assumed as the collision reference frame. The axis y along which the angular velocities \({{\varvec{\upomega }}}_1 , {{\varvec{\upomega }}}_2 \) of the pendulum parts are directed is perpendicular to the plane xz.

Fig. 3
figure 3

Forces taken into account during collision

Full size image

The Euler laws of motion in the integral form govern the behavior of the pendulum during the collision. Applying the above-mentioned assumptions, we can write

$$\begin{aligned} m_1 \left( v_{1x} (\tau )-v_{1x} (0)\right)= & {} {\bar{{H}}}-\bar{{R}}, \end{aligned}$$
(13)
$$\begin{aligned} m_1 \left( v_{1z} (\tau )-v_{1z} (0)\right)= & {} \bar{{V}}+\bar{{P}}, \end{aligned}$$
(14)
$$\begin{aligned} m_2 \left( v_{2x} (\tau )-v_{2x} (0)\right)= & {} \bar{{T}}-\bar{{H}}, \end{aligned}$$
(15)
$$\begin{aligned} m_2 \left( v_{2z} (\tau )-v_{2z} (0)\right)= & {} \bar{{F}}-\bar{{V}}, \end{aligned}$$
(16)
$$\begin{aligned} I_1 \left( \omega _{1y} (\tau )-\omega _{1y} (0)\right)= & {} \left( \bar{{V}}-\bar{{P}}\right) \frac{l_1 }{2}\sin \left( \psi _{1i}^*\right) -(\bar{{R}}+\bar{{H}})\frac{l_1 }{2}\cos (\psi _{1i}^*),\end{aligned}$$
(17)
$$\begin{aligned} I_2 \left( \omega _{2y} (\tau )-\omega _2y (0)\right)= & {} \left( \bar{{V}}l_c +\bar{{F}}d\right) \sin \left( \psi _{2i}^*\right) -\left( \bar{{H}}l_c +\bar{{T}}d\right) \cos \left( \psi _{2i}^*\right) -\bar{{T}}r, \end{aligned}$$
(18)

where \(d=l_2 +r-l_c , \quad v_{1x} ,v_{1z} ,v_{2x} ,v_{2z} \) are components of the velocities \(\mathbf{v}_1 \) and \(\mathbf{v}_2 \) of the mass centers \(C_{1}\) and \(C_{2}\), \(\omega _{1y} ={\dot{\psi }}_1 , \omega _{2y} ={\dot{\psi }}_2 \) are components of the angular velocities \({{\varvec{\upomega }}}_1 \) and \({{\varvec{\upomega }}}_2 \).

The angles \(\psi _{1i}^*=\psi _1 (t_i^{*-} )\) and \(\psi _{2i}^*=\psi _2 (t_i^{*-} )\) determine the pendulum configuration at the beginning of the ith collision.

\(\bar{{F}},\bar{{T}},\bar{{H}},\bar{{V}},\bar{{R}},\bar{{P}}\) are impulses of the components of the forces shown in Fig. 3. For instance, the impulse of the normal force F

$$\begin{aligned} \bar{{F}}=\int \limits _0^\tau {F({\tilde{\tau }})\mathrm{d}{\tilde{\tau }}} ,\quad \tau \in \left\langle {0,\tau _i^f } \right\rangle \end{aligned}$$
(19)

Equations (17) and (18) concerning the angular momentum have been written with respect to the local central axis of inertia. Equations (13)–(18) are valid for any instant \(\tau \in (0,\tau _i^f )\), whereas \(\tau _i^f \) is the instant at which the ith collision ends. The values \(\omega _{1y} (0)={\dot{\psi }}_1 (t_i^{*-} )\) and \(\omega _{2y} (0)={\dot{\psi }}_2 (t_i^{*-} )\) are known for \(i=1, 2,\ldots \), so also \(v_{1x} (0),v_{1z} (0),v_{2x} (0),v_{2z} (0)\) can be calculated.

The following commonly known relationships hold

$$\begin{aligned} \mathbf{v}_1 ={{\varvec{\upomega }}}_1 \times {\vec {OC}}_1 ,\quad \mathbf{v}_2 ={{\varvec{\upomega }} }_1 \times {\vec {OA}}+{{\varvec{\upomega }}}_2 \times {\vec {AC}}_2 , \end{aligned}$$
(20)

that reduce the number of the independent kinematic quantities in Eqs. (13)–(18) from six to two. We choose \(\omega _{1y} (\tau )\hbox { and } \omega _{2y} (\tau )\hbox { }\)as the mutually independent quantities and then rewrite the system of Eqs. (13)–(18)

$$\begin{aligned}&l_1 m_1 \Delta \omega _{1y} (\tau )\cos \left( \psi _{1i}^*\right) =2(\bar{{R}}-\bar{{H}}), \end{aligned}$$
(21)
$$\begin{aligned}&l_1 m_1 \Delta \omega _{1y} (\tau )\sin \left( \psi _{1i}^*\right) =2\left( {\overline{V}} +{\overline{P}} \right) , \end{aligned}$$
(22)
$$\begin{aligned}&l_1 m_2 \Delta \omega _{1y} (\tau )\cos \left( \psi _{1i}^*\right) +l_c m_2 \Delta \omega _{2y} (\tau )\cos \left( \psi _{2i}^*\right) =\bar{{H}}-\bar{{T}}, \end{aligned}$$
(23)
$$\begin{aligned}&l_1 m_2 \Delta \omega _{1y} (\tau )\sin \left( \psi _{1i}^*\right) +l_c m_2 \Delta \omega _{2y} (\tau )\sin \left( \psi _{2i}^*\right) =\bar{{F}}-\bar{{V}}, \end{aligned}$$
(24)
$$\begin{aligned}&I_1 \Delta \omega _{1y} (\tau )=(\bar{{V}}-\bar{{P}})\frac{l_1 }{2}\sin (\psi _{1i}^*)-(\bar{{R}}+\bar{{H}})\frac{l_1 }{2}\cos (\psi _{1i}^*), \end{aligned}$$
(25)
$$\begin{aligned}&I_2 \Delta \omega _{2y} (\tau )=\left( \bar{{V}}l_c +\bar{{F}}d\right) \sin \left( \psi _{2i}^*\right) -\left( \bar{{H}}l_c +\bar{{T}}d\right) \cos \left( \psi _{2i}^*\right) -\bar{{T}}r, \end{aligned}$$
(26)

where \(\Delta \omega _{1y} (\tau )=\omega _{1y} (\tau )-\omega _{1y} (0), \quad \Delta \omega _{2y} (\tau )=\omega _{2y} (\tau )-\omega _{2y} (0).\)

The velocity at the contact point M may be decomposed into two mutually perpendicular components in the following way

$$\begin{aligned} \mathbf{v}_M =\mathbf{s}+\mathbf{c}=s\mathbf{i}+c\mathbf{k}, \end{aligned}$$
(27)

where \(\mathbf{i}\hbox { and }{} \mathbf{k}\) are unit vectors of the axes of the collision reference frame shown in Fig. 3. The vector \(\mathbf{s}\) is called the sliding velocity, and \(\mathbf{c}\) is the closing velocity.

According to the Poisson hypothesis, we distinguish two phases of the collision. They are separated from each other by an instant \(\tau _i^m \) at which the closing velocity c is equal zero. The magnitude of the normal force F achieves its maximum at \(\tau _i^m \). The impulses of the normal force F in the first and in the second phase are coupled as follows

$$\begin{aligned} \bar{{F}}_{II} =k \bar{{F}}_m , \end{aligned}$$
(28)

where k is the coefficient of restitution, and

$$\begin{aligned} \bar{{F}}_m =\int \limits _0^{\tau _i^m } {F({\tilde{\tau }})\mathrm{d}{\tilde{\tau }}} , \quad \bar{{F}}_{II} =\int \limits _{\tau _i^m }^{\tau _i^f } {F({\tilde{\tau }})\mathrm{d}{\tilde{\tau }}} . \end{aligned}$$
(29)

The Coulomb law has been employed to describe the relationship between the friction force T and normal force F. Regarding that character of this relationship depends on the existence of the slip between the contacting bodies, we write

$$\begin{aligned} s\ne 0 \Rightarrow T=-\mu F\frac{s}{\left| s \right| }, \quad s=0 \Rightarrow T \le \mu F, \end{aligned}$$
(30)

where \(\mu \) is the friction coefficient, and \(T=\mathbf{T}\cdot \mathbf{i}\) is the projection of the vector T on the common tangent at the contact point M.

Equations (21)–(26), written for the instant \(\tau _i^f \), together with Eq. (28) and relationships (30) create the set of collision laws. They allow to determine the kinematic state of the double pendulum after ith collision.

3.4 Routh’s method and collision of double pendulum

All of the collision laws, except the friction laws, have the global nature. In other words they are written in the integral formulation and concern the whole collision. The law given by (30) is formulated for instantaneous values and due to its dual form cannot be generalized for the impulses \(\bar{{F}}\) and \(\bar{{T}}\) in a simple way, i.e., by integrating. The value of the impulse \(\bar{{T}}\) at the moment \(\tau _i^f \) depends on existence of the slip at the contact point M because the magnitude as well as the direction of the force T depend on the sliding velocity s at the contact point M. In what follows we illustrate how to solve this difficulty applying the Routh method. It should be emphasized that Routh’s method is an exact one.

In order to apply this method, we should determine the relations between the sliding and the closing velocities on one hand and the impulses of the forces at the contact point Mon the other hand. The assumption the position of the double pendulum does not change during the collision yields

$$\begin{aligned} \mathbf{v}_M (\tau )-\mathbf{v}_M (0)=\left( {{\varvec{\upomega }}}_1 (\tau )-{{\varvec{\upomega }}}_1 (0)\right) \times \vec {OA}+\left( {{\varvec{\upomega }}}_2 (\tau )-{{\varvec{\upomega }} }_2 (0)\right) \times \vec {AM,} \end{aligned}$$
(31)

for any \(\tau \in \left\langle {0,\tau _i^f } \right\rangle \).

Decomposing the vectors \(\mathbf{v}_M (\tau )\) and \(\mathbf{v}_M (0)\) in accordance with Eq. (27) we get

$$\begin{aligned} s(\tau )-s(0)= & {} -l_1 \Delta \omega _{1y} (\tau ) \cos \left( \psi _{1i}^*\right) -(r+(d+l_c )\cos \left( \psi _{2i}^*\right) \Delta \omega _{2y} (\tau ), \end{aligned}$$
(32)
$$\begin{aligned} c(\tau )-c(0)= & {} l_1 \Delta \omega _{1y} (\tau ) \sin \left( \psi _{1i}^*\right) +(d+l_c )\Delta \omega _{2y} (\tau ) \sin \left( \psi _{2i}^*\right) . \end{aligned}$$
(33)

Solving the system of Euler’s laws (21)–(26) with respect to the following quantities: \(\Delta \omega _{1y} ,\Delta \omega _{2y} ,\bar{{H}},\bar{{V}},\bar{{R}},\bar{{P}}\) and then substituting the solutions for \(\Delta \omega _{1y} (\tau )\) and \(\Delta \omega _{2y} (\tau )\) into Eqs. (32) and (33) we obtain the sought dependencies

$$\begin{aligned} s(\tau )-s(0)=\alpha _i \bar{{T}}+\varepsilon _i \bar{{F}}, \end{aligned}$$
(34)
$$\begin{aligned} c(\tau )-c(0)=\varepsilon _i \bar{{T}}+\gamma _i \bar{{F}}. \end{aligned}$$
(35)

The constants \(\alpha _i ,\varepsilon _i ,\gamma _i \) are defined as follows

$$\begin{aligned} \alpha _i =\frac{\mathrm{A}_i }{4\left| \mathbf{A} \right| }, \quad {\gamma _i =\frac{\Gamma _i }{4\left| \mathbf{A} \right| }}, \quad {\varepsilon _i =\frac{\mathrm{E}_i }{4\left| \mathbf{A} \right| }}, \end{aligned}$$
(36)

where

$$\begin{aligned} \mathrm{A}_i= & {} 4l_1^2 \cos \left( \psi _{1i}^*\right) (\left( I_2 +l_c^2 m_2 \right) \cos \left( \psi _{1i}^*\right) -l_c m_2 \left( r+(l_2 +r)\cos \left( \psi _{2i}^*\right) \right) \cos \left( \psi _{1i}^*-\psi _{2i}^*)\right) \\&+\left( 4I_1 +l_1^2 \left( m_1 +4m_2 \right) \right) \left( r+(l_2 +r)\cos \left( \psi _{2i}^*\right) \right) ^{2}\\&-2l_1^2 l_c m_2 \left( r+(l_2 +r)\cos \left( \psi _{2i}^*\right) \right) \left( \cos (2 \psi _{1i}^*-\psi _{2i}^*\right) +\cos \left( \psi _{2i}^*\right) ),\\ \Gamma _i= & {} \left( 4I_1 +l_1^2 \left( m_1 +4m_2 \right) \right) (l_2 +r)^{2}\sin ^{2}\left( \psi _{2i}^*\right) +4l_1^2 \sin ^{2}\left( \psi _{1i}^*\right) \left( I_2 +l_c^2 m_2 -l_c m_2 (l_2 +r)\sin ^{2}\left( \psi _{2i}^*\right) \right) \\&-2l_1^2 l_c m_2 (l_2 +r)\left( 2\sin ^{2}(\psi _{1i}^*)\sin ^{2}\left( \psi _{2i}^*\right) +\sin \left( 2 \psi _{1i}^*\right) \sin \left( 2 \psi _{2i}^*\right) \right) , \\ \mathrm{E}_i= & {} 2l_1^2 (l_c m_2 (l_2 +r\left( 1+\cos \left( \psi _{2i}^*\right) \right) -I_2 -l_c^2 m_2 ) \sin (2 \psi _{1i}^*) \\&+\,r\left( 4l_1^2 l_c m_2 \sin ^{2}\left( \psi _{1i}^*\right) -(l_2 +r) \left( 4I_1 +l_1^2 (m_1 +4m_2 )\right) \right) \sin \left( \psi _{2i}^*\right) \\&+\,(l_2 +r)\left( {2l_1^2 l_c m_2 -\frac{l_2 +r}{2}\left( 4I_1 +l_1^2 \left( m_1 +4m_2 \right) \right) } \right) \sin \left( 2 \psi _{2i}^*\right) , \end{aligned}$$

the determinant \(\left| \mathbf{A} \right| \) is defined by Eq. (6).

The constants \(\alpha _i,\quad {\gamma _i } \quad {\varepsilon _i}\) depend on the geometrical and inertial parameters of the pendulum but also on its configuration at the beginning of the collision what means that they must be determined separately for each collision.

The Routh method has a clear geometrical interpretation in the impulse space. In the case of planar motion, this space is two-dimensional. According to the nature of a normal force F, its impulse is always nonnegative. Therefore, we will say further about the impulse semi-plane.

Assuming in Eq. (34) \(s(\tau )=0\), one can derive the condition concerning the collision without slip. A line called the line of sticking corresponds to this condition on the semi-plane. Similarly, supposing \(c(\tau )=0\) in Eq. (35), we obtain the equation of the line of maximum compression. In turn, the relationship between impulses \(\bar{{F}}\) and \(\bar{{T}}\), when \(s(\tau )\ne 0\), derived from Eq. (30) has the form

$$\begin{aligned} \bar{{T}}=-\mu \bar{{F}}\frac{s(0)}{\left| {s(0)} \right| }. \end{aligned}$$
(37)

The line of friction is its image on the impulse semi-plane. It should be noted that all these lines are strictly determined by the configuration state of the pendulum as well as the velocity \(\mathbf{v}_M \) at the moment in which the collision starts. Mutually, location of these lines is of decisive importance for the values of impulses at the end of each collision. There are some possibilities of this arrangement. Five of them are presented in Fig. 4.

Fig. 4
figure 4

Interpretation of Routh’s method on the impulse semi-plane

Full size image

The axes of the coordinate system are scaled in the units of the force impulse. The starting point of the line of friction (depicted by bold solid line) lies always at the origin of the coordinates system and represents the beginning of the collision (we assume that at \(\tau =0\), the slip always appears). On the graph 4a, the line of friction and the line of sticking (depicted by dotted line) do not cross each other in the first phase of collision (i.e., on the left side of the line of maximum compression \(c = 0\)). Therefore, the point \(\Gamma _m \) in which the line of friction and the line of maximum compression intersect each other determines the end of the first phase of the collision. In accordance with Eq. (16), the abscissa of the point \(\Gamma _m \) multiplied by \((1+k)\) specifies the line of end of collision (it is always parallel to the vertical axis). The line of friction crosses it at the point \(\Gamma _f \) the coordinates of which are sought values of the impulses \(\bar{{F}}\) and \(\bar{{T}}\) at the end of the collision. On the graphs b) and c), the line of friction crosses the line of sticking in the first phase of the collision. That means the sliding velocity s becomes then equal zero. The relation between the angles \(\varphi \) and \(\varphi _s \) is of decisive importance for the possibility of the continuation of the collision which is accompanied by the slip. If \(\varphi >\varphi _s \), what is shown in Fig. 4b, the slip vanishes and the collision without the sliding lasts to the end of the contact with the obstacle. Since that moment, the line of sticking represents the collision and its crossing-points with the lines of maximum compression as well as the line of end of collision determine the point \(\Gamma _f \). Otherwise, what is shown on the graph 4c, the friction forces are too small to eliminate the slide between the disk and the obstacle. So, the disk, having changed the direction of motion, still slides on the obstacle. The change of the sign of the vectors s and T causes that on the line of friction appears the discontinuity in slope. Graphs 4d and 4e concern the situation when the line of friction crosses the line of sticking in the second phase of the collision. For each of the graphs shown in Fig. 4 exists its counterpart that presents an arrangement with the line of friction which is symmetric in respect of the horizontal axis.

4 Results

Let us consider the motion of double pendulum whose parameters are as follows: \(m_1 =3.2\,\hbox {kg,}\; m_2 = 3.8\,\hbox {kg,}\; l_1 =0.5\, \hbox {m,}\; l_2 = 0.6\,\hbox {m,} \;r=0.05\,\hbox {m}\). The mass center of the second pendulum part is distant from the joint A by \(l_c \approx 0.3627\,\hbox {m}\). The moments of inertia of the both pendulum parts with respect to their central principal axes are: \({I_1 \approx 6.76 \times 10^{-2}\,\hbox {kg}\, \hbox {m}^{\mathrm {2}},} \quad {I_2 \approx 0.164\,\hbox {kg}\, \hbox {m}^{\mathrm {2}}}\). During the motion, the pendulum collides with a fixed obstacle that is placed at the distance \(D = 0.9\) m from the point O. The value of the coefficient of restitution k was assumed as 0.9. It is assumed that do not act the external torques and also there is no damping at the both joints in order to focus on the influence of the collisions on the pendulum motion. The results of two simulations will be presented farther on. These two simulations differ from each other only in the occurrence of friction force between the obstacle and the disk. One of them concerns the case when the pendulum collides with the obstacle having perfectly smooth surface (\(\mu =0)\). In the second simulation, the value of the friction coefficient \( \mu =0.15.\) The values describing the initial state of the pendulum were assumed for the both simulations the same. They are listed below:

$$\begin{aligned} \psi _1 (0)=140^{\circ }, \quad \psi _2 (0)=-90^{\circ }, {\dot{\psi }}_1 (0)=1.2\,\hbox {rad/s,} \quad {\dot{\psi }}_2 (0)=-0.5\, \hbox {rad/s}. \end{aligned}$$
Fig. 5
figure 5

Stepwise changes of mechanical energy of the pendulum

Full size image
Fig. 6
figure 6

Changes in time of the angular velocities of the rod OA

Full size image
Fig. 7
figure 7

Changes in time of the angular velocities of the second pendulum part

Full size image

In Fig. 5, the loss of mechanical energy versus time of motion is shown for the case with the friction (red line) and without the friction (black line). Under the given assumptions (no torques and no damping), the system may lose the energy only as a result of collisions. Indeed, we can see that between the collisions the total energy is constant. The energy decreases stepwise after each contact with the obstacle. For comparison, the energy of the pendulum at the stable equilibrium position \(\psi _1 =0\) and \(\psi _2 =0\) is about of −40.007 J. The both graphs shown in Fig. 5 differ from each other. The numbers of the impacts with the obstacle are different. The total energy of the pendulum after the first collision decreased much more when the friction force was taken into account. The comparison, concerning the first collision, is justified because only then, the kinematic state of the pendulum just before the collision is the same for the both considered cases. Greater global energy loss which is observed in the case when the friction force exists is also a result of the bigger number of collisions. It can be seen that the pendulum collides six times in time of simulation for the case \(\mu =0\), and ten times, when \( \mu =0.15.\)

In Figs. 6 and 7, the time histories of the angular velocities of the both part of the pendulum are shown. In these figures, the graphs, drawn in black, concern the case when the friction force does not act during the collisions, whereas the graphs drawn in red—concern collisions with the friction force. When it is assumed that the obstacle is perfectly smooth, the angular velocities of the pendulum parts are subject to the discontinuous changes as a result only of the oblique eccentric collision. Appearance of the friction force at the contact point is an additional circumstance which causes the discontinuities of the angular velocities. The visible differences between the time dependencies of angular velocities in both compared cases involve the shape of the graphs and also the number of the discontinuity points (six and ten, respectively).

The vertical P and horizontal R components of the reaction force at the joint O as functions of time are presented in Fig. 8. As previously, the black lines refer to the case without the friction force, and the red lines concern the case when \( \mu =0.15\). The divergence between the graphs (presented in one figure), which is caused by the influence of the friction force, becomes more and more visible after each subsequent collision.

Fig. 8
figure 8

Changes in time of reaction force components at the joint O

Full size image

The time histories of the vertical Vand horizontal H components of the internal force at the joint A are shown in Fig. 9. The black lines refer to the case without the friction force, whereas the red lines—the case when the friction coefficient \( \mu =0.15\). The differences observed for the both components deepen with time, i.e., with the growing number of collisions.

Fig. 9
figure 9

Changes in time of reaction force components at the joint A

Full size image

5 Conclusions

Models of collision phenomena taking into account friction forces at contact are more suitable for real problems. The obtained results indicate that the friction forces have a significant impact on the collisions.

Possibility of the non-sliding type of contact significantly complicates the solving of the problem, even for the relatively simple models with only one point of contact. In the paper, the Routh method has been applied to solve the problem concerning the collision of multi-body system. Combination of the exact method with numerical calculations in the framework of the piecewise smooth model allows us to investigate multiple collisions of the mechanical system taken under consideration. The proposed model employing the Routh method is relatively simple. This approach does not require neither the formulating nor solving the differential equations which describe the collisions. The process of collision is solved on the base of the algebraic formulation.

The numerical simulations have been done using the original software written in Fortran 95.