Precise estimation of pressure–temperature paths from zoned minerals using Markov random field modeling: theory and synthetic inversion

Abstract

The chemical zoning profile in metamorphic minerals is often used to deduce the pressure–temperature (P–T) history of rock. However, it remains difficult to restore detailed paths from zoned minerals because thermobarometric evaluation of metamorphic conditions involves several uncertainties, including measurement errors and geological noise. We propose a new stochastic framework for estimating precise P–T paths from a chemical zoning structure using the Markov random field (MRF) model, which is a type of Bayesian stochastic method that is often applied to image analysis. The continuity of pressure and temperature during mineral growth is incorporated by Gaussian Markov chains as prior probabilities in order to apply the MRF model to the P–T path inversion. The most probable P–T path can be obtained by maximizing the posterior probability of the sequential set of P and T given the observed compositions of zoned minerals. Synthetic P–T inversion tests were conducted in order to investigate the effectiveness and validity of the proposed model from zoned Mg–Fe–Ca garnet in the divariant KNCFMASH system. In the present study, the steepest descent method was implemented in order to maximize the posterior probability using the Markov chain Monte Carlo algorithm. The proposed method successfully reproduced the detailed shape of the synthetic P–T path by eliminating appropriately the statistical compositional noises without operator’s subjectivity and prior knowledge. It was also used to simultaneously evaluate the uncertainty of pressure, temperature, and mineral compositions for all measurement points. The MRF method may have potential to deal with several geological uncertainties, which cause cumbersome systematic errors, by its Bayesian approach and flexible formalism, so that it comprises potentially powerful tools for various inverse problems in petrology.

Appendix

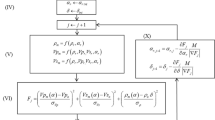
It is essential to estimate the precise P–T path that the hyperparameters, $\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,$ and $\sigma_{Tm}^2,$ are determined. This is the most important advantage of the Bayesian approach. The hyperparameters, $\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,$ and $\sigma_{Tm}^2,$ can also be regarded as random thermodynamic variables. Then, we need to determine the set of hyperparameters that maximize the posterior probability $p(\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2 |\{ X_{1}^i \} ,\{ X_{2}^i \} ) .$ Using Bayes’ theorem,

$$ p(\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2|\{ X_{1}^i \} ,\{ X_{2}^i \} )= \frac{{p(\{ X_{1}^i \} ,\{ X_{2}^i \} |\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2) \cdot p(\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2)}}{{p(\{ X_{1}^i \} ,\{ X_{2}^i \} )}}. $$

(19)

Here, the following equation has mathematical equality:

$$ \begin{aligned} &p(\{ X_{1}^i \} ,\{ X_{2}^i \} |\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2) \\ &=\int \int p(\{ X_{1}^i \} ,\{ X_{2}^i \} ,\{ P^i\} ,\{ T^i\} |\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2) \, d\{ P^i\} d \{T^i\}. \end{aligned} $$

(20)

This type of operation is referred to as marginalization. We define the negative logarithm of the posterior possibility as the free energy function using Eqs. 19 and 20 as

$$ \begin{aligned} F(\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2) &\equiv -\,\hbox{ln}\,p(\{ X_{1}^i \} ,\{ X_{2}^i \} |\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2) \\ &= -\,\hbox{ln}\,\left\{\int \int \hbox{exp} \left\{-E(\{ P^i \} ,\{ T^i \} ,\sigma_{1n}^2,\sigma_{2n}^2,\sigma_{Pm}^2 ,\sigma_{Tm}^2)\right\} \, d\{ P^i\} d \{T^i\} \right\} + C, \end{aligned} $$

(21)

where $E(\{ P^i \} ,\{ T^i \},\sigma_{1n}^2,\sigma_{2n}^2,\sigma_{Pm}^2 ,\sigma_{Tm}^2)$ is the evaluation function defined by Eq. 16, and C is a constant independent of $\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,$ and $\sigma_{Tm}^2.$

In order to search the set of hyperparameters that minimize $F(\sigma_{1n}^2, \sigma_{2n}^2, \sigma_{Pm}^2,\sigma_{Tm}^2),$ the steepest decent method was used in the present study. The slope of the free energy F to the hyperparameter σ² can be expressed as

$$ \begin{aligned} \frac{{\partial F}}{{\partial \sigma^2}} &= \frac{\displaystyle {\int \int \frac{{\partial E}}{{\partial \sigma^2}} \cdot{\exp} \left\{-E\right\}\, d\{ P^i\} d \{T^i\}}} {\displaystyle {\int \int\hbox{exp} \left\{-E\right\}\, d\{ P^i\} d \{T^i\}}} \\ &= {\int \int \frac{{\partial E}}{{\partial \sigma^2}} \cdot p(\{ P^i \} ,\{ T^i \} |\{ X_{1 }^i \} ,\{ X_{2 }^i \} ) } \, d\{ P^i\} d \{T^i\} \\ &= \left \langle \frac{{\partial E}}{{\partial \sigma^2}} \right \rangle _{p(\{ P^i \} ,\{ T^i \} |\{ X_{1 }^i \} ,\{ X_{2 }^i \} )}, \end{aligned} $$

(22)

where $\langle g\rangle _{h}$ indicates the expectation value of g for the probability distribution h. This type of equation can be written for every hyperparameter. Hence, the calculation of the gradients of the free energy F to the hyperparameters results in the calculation of the expectation values of $\partial E/\partial \sigma^2$ for the posterior probability distribution $p(\{ P^i \} ,\{ T^i \} |\{ X_{1 }^i \} ,\{ X_{2 }^i \} ).$ In the present study, the Metropolis algorithm, which is a type of MCMC method, was used to numerically calculate the expectation value (Metropolis et al. 1953). In the algorithm, numerous candidate sets of {P ⁱ} and {T ⁱ} are generated to produce the posterior probability distribution $p(\{ P^i \} ,\{ T^i \} |\{ X_{1 }^i \} ,\{ X_{2 }^i \} ).$ Consequently, the MAP and PM solutions of {P ⁱ} and {T ⁱ} can be simultaneously obtained in the process of hyperparameter estimation.