Filling the matrix: an ANOVA-based method to emulate regional climate model simulations for equally-weighted properties of ensembles of opportunity

Abstract

Collections of large ensembles of regional climate model (RCM) downscaled climate data for particular regions and scenarios can be organized in a usually incomplete matrix consisting of GCM (global climate model) x RCM combinations. When simple ensemble averages are calculated, each GCM will effectively be weighted by the number of times it has been downscaled. In order to facilitate more equal and less arbitrary weighting among downscaled GCM results, we present a method to emulate the missing combinations in such a matrix, enabling equal weighting among participating GCMs and hence among regional consequences of large-scale climate change simulated by each GCM. This method is based on a traditional Analysis of Variance (ANOVA) approach. The method is applied and studied for fields of seasonal average temperature, precipitation and surface wind and for the 10-year return value of daily precipitation and of 10-m wind speed for a completely filled matrix consisting of 5 GCMs and 4 RCMs. We quantify the skill of the two averaging methods for different numbers of missing simulations and show that ensembles where lacking members have been emulated by the ANOVA technique are better at representing the full ensemble than corresponding simple ensemble averages, particularly in cases where only a few model combinations are absent. The technique breaks down when the number of missing simulations reaches the sum of the numbers of GCMs and RCMs. Also, the method is only useful when inter-simulation variability is limited. This is the case for the average fields that have been studied, but not for the extremes. We have developed analytical expressions for the degree of improvement obtained with the present method, which quantify this conclusion.

1 Introduction

Regional climate model (RCM) downscaling of global climate model (GCM) output is a most frequently used method to obtain geographically detailed and physically consistent information of local climate change effects (Giorgi 2019). It is a foundation for the possibility of climate services to have robust information on local geographical scale of future climate change (Hewitt et al. 2021).

Many different GCM simulations are available for downscaling, and many RCMs exist, which can perform such downscaling. In order to minimize effects of both model biases and internal climate variability on conclusions drawn from downscaling simulations, many different GCM simulations need to be downscaled, preferably with many different RCMs.

RCM simulations require not just boundary conditions from GCMs but also a considerable computational effort, and therefore it is not feasible to perform simulations for all combinations of GCM simulations and RCM models. Traditionally, there has not been a synchronized strategy for how to combine GCMs with RCMs in order to obtain a matrix with a homogeneous use of plausible GCMs. Rather, such matrices are ensembles of opportunity, where pragmatic circumstances have decided which simulations have actually been performed (McSweeney et al. 2012). In spite of this, through a considerable international effort within CORDEX [the COordinated Regional climate Downscaling EXperiment, Giorgi and Gutowski (2015)], combination matrices between the most frequently used GCMs and RCMs are being constructed for all continents. One of the largest efforts has been concerned with a simulation domain covering Europe in around 12 km grid distance, in the EURO-CORDEX community initiative (Jacob et al. 2020). Currently a matrix for 3 RCP (Representative Concentration Pathways) forcing scenarios, 10 GCMs and 13 RCM versions containing a total of 124 simulations exist.

In conventional ensemble analyses, the existing ensembles of opportunity will give an unequal weight to the various GCMs caused by the quite arbitrary distribution of downscaling simulations for each GCM. Various methods for assessing characteristics of such ensembles of opportunity have been tested. This includes both techniques to comprehensively analyse the existing simulations and methods to artificially fill up matrices by statistical methods. Alternatively, methods to reduce size while attempting to retain as much of the uncertainty characteristics as possible are also used. A few examples include: Kendon et al. (2010), who used a linear pattern-scaling method for providing climate projections at the local scale in RCMs for different driving GCMs considering also untried GCM–RCM combinations and Chadwick et al. (2011) who used artificial neural networks to fill up a sparsely filled GCM-RCM matrix. By utilizing the full time series in a functional data analysis method based on Euclidian distances between simulated trajectories of change and their first derivatives, Holtanová et al. (2019) emphasized the need for carefully assessing the choice of RCMs in any applied research. Also Bayesian techniques have been used, such as in Evin et al. (2019), who show that this can be used also to propagate uncertainty due to missing information in the resulting estimates. Analysis of variance (ANOVA) is another method that has been extensively used to characterize the dependence of the ensemble mean characteristics on GCMs, RCMs and internal variability [e.g. Déqué et al. (2007, 2012), Yip et al. (2011) and Christensen and Kjellström (2020)]. Examples of how reduction of the number of simulations can be used are given by Mendlik and Gobiet (2016) and Wilcke and Bärring (2019), both applying clustering techniques.

In this study we examine a method, where “holes” in a GCM/RCM combination matrix can be emulated, based on information from the existing simulations in the matrix. The method is based on a standard ANOVA analysis with GCM choice, RCM choice, and simulation period as 3 determining factors of a field value, and works for N_G×N_R matrices where at least N_G + N_R  − 1 simulations exist, N_G and N_R being the number of GCMs and RCMs, respectively. We study the accuracy of the emulation and the effect of holes on both simple ensemble means and emulated ensemble means for a complete matrix consisting of 5 GCMs and 4 RCMs for the RCP8.5 emission scenario and for the 12 km European EURO-CORDEX domain, where we analyse up to 1000 combinations of simulations for each number of holes; see Christensen and Kjellström (2020) for details about the ANOVA analysis of these 20 simulations.

2 Methods and data

By use of an ANOVA analysis (e.g. Déqué et al. 2007; Yip et al. 2011; Christensen and Kjellström, 2020) it is possible under certain conditions to “fill holes” in a matrix, i.e., calculate emulated values for model combinations, which have not yet been filled by an actual simulation, based on an incomplete matrix of actual simulations. The terms of an ANOVA analysis determining the effect of period in a scenario, of GCM, and of RCM, are listed in Table 1. The strategy of ANOVA is a separation of the influences of various factors; here period, GCM choice and RCM choice, into average linear terms and multi-index cross terms. For instance, the G term will give the effect of the GCM choice averaged over RCMs and periods etc. Interdependence of RCM and GCM choice will be in the GR terms for each combination of GCM and RCM. Given trustworthy values of the linear (single-index) terms (S_i, G_j and R_k from Table 1) in an ANOVA analysis, we can emulate values for the holes. For this purpose we postulate that there is no specific effect of the GCM-RCM combination in question, but that it is simply a sum of a period-specific, a GCM-specific and an RCM-specific term; since there is no way to estimate the single-simulation specific ANOVA contribution of an unavailable simulation, this contribution will be set to zero, and the resulting equations will be solved with the values in the positions without simulations as the unknown. In other words, we find the best possible value based on individual contributions from GCM and RCM identities.

Table 1 Formulae for the various ANOVA terms, under the requirement that all terms sum to zero over any single index

The hole filling technique operates on each field, season, and point individually. We will use the notation Y_ijk for field values for a period i which is 1 for the present-day 30-year period and 2 for the future 30-year period; GCM is indexed with j and RCM with k; the notation is the same, whether the value is known or is missing. Note that averaging over each 30-year period is implicit. In this study present and future periods either both exist or both do not exist.

The ANOVA method will write each individual term as a sum of linear terms and cross terms,

$$ Y_{ijk} = M + S_{i} + G_{j} + R_{k} + SG_{ij} + SR_{ik} + GR_{jk} + SGR_{ijk} $$

(1)

The requirement that all terms sum to zero over an explicit index leads to the term definitions in Table 1. When a simulation is missing, we will now set the GCM-RCM-specific terms to zero, SGR_ijk = 0 and GR_jk = 0 for a hole corresponding to GCM j and RCM k and valid for both periods i = 1,2; this corresponds to the explicit equation

$$ 0 = Y_{ijk} - Y_{ij.} - Y_{i.k} - Y_{.jk} + Y_{i..} + Y_{.j.} + Y_{..k} - Y_{ \ldots } $$

(2)

where the dots indicate averaging over a dimension. Since both total means and single-RCM or single-GCM means enter this equation, a fully coupled linear system of equations will result from a situation with several holes; these means will contain contributions from both the emulated value at ijk and from all other emulated values. This equation system is mostly but not always solvable.

The technique described above is now applied to seasonal average fields obtained from 20 simulations from the EURO-CORDEX initiative (Jacob et al. 2014). The ANOVA analysis of these simulations, which form a complete matrix with 5 GCMs and 4 RCMs, has been described in Christensen and Kjellström (2020); the analysis in that paper was performed for the 19 models available at the time, the remaining simulation emulated as described in that study. In the current study, all 20 models are available. The simulations have also been analysed in terms of performance for the historical climate (Vautard et al. 2020) and for climate change (Coppola et al. 2021). The models are listed in Table 2.

Table 2 Global and regional models analysed in this study

For a number n of holes, there are a total of 20!/(n! (20-n)!) different combinations. For 1 and 2 holes this number is 20 and 190, respectively; these matrices are all solvable (see below). We have performed the calculation for all configurations with one and two holes. For larger numbers we have limited ourselves to 1000 randomly chosen different solvable configurations with the given number of holes. For each of the resulting matrices, the hole-filling algorithm is applied.

In order to examine significance related to an ANOVA analysis, equality of interannual variance is a general prerequisite. We have not performed any formal test for such homoscedasticity but we note that, for the fields considered, pointwise ratios between maximum and minimum variability are sometimes above 2. This may, as a rule of thumb, be considered as an upper level for equal variance (Yang et al. 2019) implying that this general assumption is violated. However, as the ratio is most often less than 4 and as sample sizes are equal, which acts to minimize the influence of this type of violation, we neglect any influence of this on the results. Also, we note here that the ANOVA technique is used here to emulate non-existing simulations and that significances associated with its terms are of lesser importance.

2.1 Matrix properties

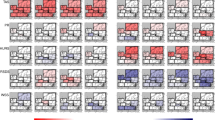
We find minimum requirements for properties of the GCMxRCM population matrix (one if a simulation exists, otherwise zero) for enabling unique calculations of emulated values for the empty holes. Examples of population matrices where the procedure does not work are instances with no simulations at all for a specific GCM or a specific RCM. Also, situations where the matrix can be split into two non-connected sub-matrices are invalid; see examples in Fig. 1. Conceptually: If one sub-matrix has generally much higher values than a remaining disconnected sub-matrix, there is no way to know if the set of GCMs or the set of RCMs are the reason; this is reflected in a redundancy in the set of equations, which makes the solution non-unique.

Fig. 1

Examples of four GCM × RCM matrices with twelve holes. The two in the top are solvable. The bottom two not: The first can be split into two disconnected sub-matrices as indicated by yellow and green colours; the second has a row without simulations (red)

The minimum necessary properties that each GCM and also each RCM is represented at least once, and that each simulation shares at least either the same GCM or the same RCM with others, and finally that no independent sub-matrices exist, lead to a minimum number of existing simulations of N_GCM + N_RCM – 1. At the same time, it is straightforward to generalise the examples above to show that this number is also sufficient to solve the equation. So, even if there may exist other rules than those above, which may disqualify particular combination matrices, it still holds that the minimum number of existing simulations for applying the method studied is the number above, the sum total of both kinds of models, minus one.

For the current situation of five GCMs and four RCMs the maximum number of holes turns out to be twelve. It means that for a 5 × 4 GCM-RCM matrix we need at least eight simulations to have a chance to build the entire matrix with this ANOVA technique. Of course it does not mean that the reconstruction of the missing element would be satisfactory in practice, but that it is a minimum number of simulations required.

An example of the kind of equation system to solve is the following, where we have two holes, Y_ij’k’ and Y_{ij’’k’’} and assume that j’ ≠ j’’ and k’ ≠ k’’, i.e., that the holes represent different GCMs as well as different RCMs. Let’s look at the control period i = 1. In Eq. 2 only the last term, the total ensemble mean, connects the two holes. The two-dimensional system can then be expressed in the form

$$ \left[ {\begin{array}{*{20}c} {\left( {N_{G} - 1} \right)\left( {N_{R} - 1} \right)} & 1 \\ 1 & {\left( {N_{G} - 1} \right)\left( {N_{R} - 1} \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {Y_{1j^{\prime}k^{\prime}} } \\ {Y_{1j^{\prime\prime}k^{\prime\prime}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {B_{1j^{\prime}k^{\prime}} } \\ {B_{1j^{\prime\prime}k^{\prime\prime}} } \\ \end{array} } \right] $$

(3)

where the number of GCMs is N_G = 5, the number of RCMs is N_R = 4, and the B indicate expressions, which do not depend on the unknown hole values, only on various averages of existing simulation data for the point, season, and field in question. The exact definitions can be determined from Eq. 2.

It is important for the practical feasibility of using this method, that only one matrix inversion is necessary for each model combination. The only operation proportional to the number of points and seasons is the matrix multiplication necessary for obtaining the Y values corresponding to matrix holes.

3 Results and discussion

3.1 Effects of missing simulations

We want to study to which degree sparsely filled matrices, where holes are synthetically filled, can replicate features of the full matrix. Any simulation-specific contribution to the field for the simulation being removed, like effects of internal variability, as represented in the corresponding full-matrix GR and SGR terms, can in no way be emulated, as this information is removed from the underlying data along with the simulation; this includes effects of GCM-RCM dependency for the combination being removed. Here our aim is to investigate the deterioration of the emulated values as a function of the number of holes.

An example is shown in Fig. 2, where we look at the ensemble mean temperature averaged over both periods (Y_.jk) as well as the mean climate change (Y_2jk – Y_1jk) separately at a seasonal basis, and calculate root-mean-square differences of values over the model domain as well as over j and k. For each matrix, the holes have been filled as described above.

Fig. 2

Average RMS deviation (deg. C) from one-hole emulated values of seasonal mean temperature as a function of the number of excess holes (the number of holes more than the one hole we compare to, for each hole in each configuration). Up to 1000 configurations have been examined for each number of holes (see text). More than 11 excess holes, i.e., a total of less than 8 existing simulations, cannot be treated with this method. Solid lines: mean climate. Dashed lines: Future minus mean, i.e., 50% of the climate change signal. DJF blue, MAM green, JJA orange, SON black

For a number n of holes, we look at each jk combination in turn, find the matrices where jk is one of the holes, and calculate the average squared deviation from the 1-hole emulated value across all grid points. We average this quantity over all matrices with a hole at jk, and after that over all jk combinations. In the end we have, for each field and season investigated, a measure of the mean squared deviation from the best emulated value, as a function of n. Taking the square root we have a measure of the deviation from the emulated value based on only one hole. The unit is the same as that of the quantity examined.

In Figs. 3, 4 and 5 we present results from the analysis of our collection of configurations for the three fields analysed: Seasonal mean temperature, mean precipitation, and mean 10 m wind speed. For a given configuration, we compare the emulated field with the corresponding emulated field when only the combination in question is missing, i.e., the one-hole situation. The reason for this procedure is the intent to not include the specific characteristics of this combination but only look at the deterioration of the emulation as more and more actual simulations are removed.

Fig. 3

Like Fig. 2, but for precipitation (mm/d)

Fig. 4

Like Fig. 2, but for average 10-m wind speed (m/s)

Fig. 5

Top: Deviation of one direct 8-model average DJF temperature from true 20-model average (deg. C). Bottom: Deviation of emulated 20-value average based on the same 8 models from true 20-model average. The left column shows differences in mean climate, the right column shows differences in (full) climate change

The curves show the RMS average over missing simulations, over all matrices, and over points. Full curves show results for mean climate, whereas dashed curves show results for climate change.

The shapes of these curves are quite similar: A large jump in deviation appears when 1 extra hole is introduced. After that there is a slight upwards curve as a function of the number of holes, until we reach the maximum possible number of 11 extra holes, where we note that the steepness of the curves increases. The average deviation over the full domain is of the order of 5–10 times larger for 11 extra holes compared to 1 extra hole both for the mean and for the climate change signal. We also note that there are differences in how large the errors are between the seasons. Winter stands out with the largest error for the mean climate for all three variables. Conversely, spring shows the smallest error. For the climate change signal the difference between the seasons are less consistent. However, winter stands out also here with larger errors for temperature and wind speed than in any of the other seasons.

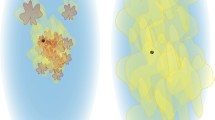
A possible contribution to the large deviation for winter is illustrated in Fig. 5, bottom row: The differences between emulated and actual temperatures are quite large for sea-ice covered areas in the Barents Sea and north of Iceland. These regions were also recognised in Christensen and Kjellström (2020) as areas with a large SGR cross-term in the ANOVA analysis. In other words, since the behaviour over sea ice is influenced by the particular combination of the GCM sea ice distribution and the RCM physics, the current emulation procedure will not be well suited to describe such areas due to the basic assumption that SGR is set to zero for the missing simulations.

3.2 Estimating ensemble averages

A different way to approach the issue of added value from the hole-filling procedure is to look at how to best estimate the complete matrix mean including all 20 simulations from a set of fewer available simulations. This complete matrix mean is not necessarily closer to the physical truth than a simple average; it does, however, introduce a more “democratic” weighting of both the RCMs and the GCMs involved. In a pure ensemble of opportunity, each GCM will have an effective weight corresponding to the number of times it has been downscaled, and correspondingly for each RCM. With the technique being developed here, however, there will be equal weight between the GCMs chosen to be represented in the matrix and also between the RCMs. We have therefore analysed two strategies for approximating the filled-matrix ensemble average from an incomplete matrix: The simple ensemble-of-opportunity “direct” average of the existing simulations in the incomplete matrix, and the mean obtained from matrix filling with emulated values filled into holes as outlined in this study. As opposed to Sect. 3.1 we will go back to a comparison with the full matrix.

In the presentation of this section we will concentrate on temperature for illustration purposes. In Fig. 5 we see an example for one arbitrary 5 × 4-member matrix with 12 holes and only 8 simulations. It is clear that the direct 8-member ensemble-of-opportunity mean is mostly much farther from the complete-matrix “truth” than it is possible to achieve with the matrix-filling method used here. Further, we note relatively poor performance for the direct-average method over sea in general, where the emulation technique gives equal weight to the SST values of each GCM, just as in the true full-matrix average. A notable exception is the sea ice covered areas north of Russia and of Iceland, where the matrix filling technique is further from the true average than the direct average. The emulated results are worse in some northern sea-ice covered areas, where Christensen and Kjellström (2020) saw large difference between individual simulations and their emulated counterparts, i.e., a large role of specific GCM-RCM combinations. This is probably related to specifics of sea ice description in the 8 models used, compared to the total ensemble. This needs further investigation.

To systematise this also for other number of holes and other seasons, we plot in Fig. 6 the RMS average over all points and all matrices of deviations as those shown in Fig. 5 as a function of the number of holes. It is clear from the figure that the matrix-filling procedure creates a matrix that is much more similar to the original full matrix compared to the direct mean of any ensemble of opportunity consisting of fewer members. This is true for all numbers of holes investigated both for the mean climate (top panel) and for the climate change signal (bottom panel).

Fig. 6

RMS deviations over points and bootstrapped simulations of deviation from true 20-model complete matrix average seasonal mean temperatures as a function of the total number of holes. Full lines: Deviation of direct average of ensembles from 20-model truth; dashed lines: Deviation of means over emulated full matrix from 20-model truth. Top panel: Mean climate. Bottom panel: climate change. DJF blue, MAM green, JJA orange, SON black

Adding perspective, in Fig. 7 we add a curve spanning all possible numbers of holes, where 1000 different combination matrices (20 for 1 and 19 missing simulations, 190 for 2 and 18 missing simulations) have been chosen randomly, since there are no solvable matrices for more than 12 holes. Note the small discrepancy around 10–12 holes between the mean deviation of completely random but different combinations and mean deviation of only solvable different combinations—this must be because non-solvable combinations will frequently miss an RCM or a GCM entirely, hence deviating more from the true average than combinations where all models are represented; ensembles of solvable matrices are more homogeneous among models and therefore somewhat closer to the true average.

Fig. 7

Extension of Fig. 6 with simple averages of random ensembles added. Left column: Mean climate. Right column: Climate change. Top: Temperature (K). Middle: Precipitation (mm/day). Bottom: Wind speed (m/s). The legend applies to all panels. See text

A comparison between the present hole-filling averaging and the simple averaging is detailed in Fig. 8, showing the ratio between the two measures for the same sets of combination matrices. Here, we show the results for temperature, precipitation, and 10-m wind speed; we will also investigate 10-year return values of daily precipitation and 10-m wind speed. It can be seen that the improvement taking the emulated mean versus the primitive mean is always largest when only a few simulations are missing. For temperature we can estimate the true ensemble mean of both mean climate and climate change around 3 times better with the ANOVA-based technique than we do with simple averaging of available models when the matrix is almost complete, decreasing to around a factor of 2 when we reach the limits of the current technique. For precipitation the situation is similar but with somewhat smaller ratios, falling from around 2.5 to around 1.5. For wind speed we see large improvements for the mean climate, similar to temperature, whereas there is hardly any improvement for climate change. For the extremes investigated we find that this method does not add any improvement over the primitive average.

Fig. 8

Ratio between the square root of mean over combinations of squared difference between incomplete-ensemble mean and true ensemble mean, and the corresponding squared difference between emulated-ensemble mean and true ensemble mean. Solid lines: mean climate. Dashed lines: Climate change signal. DJF blue, MAM green, JJA orange, SON black. Top panel: Temperature. Middle panel: Precipitation. Bottom panel: 10 m wind speed

3.3 Mathematical modelling of ensemble averaging methods

To put the results into perspective, let us estimate which dependence on the number of holes we may expect. We will for a moment assume that the ensemble can be viewed as following a statistical distribution with a constant spread around a mean, which we for the moment set to zero. Let there be N_G x N_R = N members in total of the matrix, and let us examine m holes.

The emulated values will be located around the same mean, but have a variance, which is considerably lower, at least for large matrices, since they are determined by summation rules involving sums of many existing simulations. Simple calculations of the dependence on m show that the deviation is proportional to $\sqrt{m}$ for the emulated mean, and to $\sqrt{m /\left(N-m\right)}$ for the direct mean; the emulated mean will have a smaller deviation than the direct one, and the ratio between them will grow with m. Let us look at a matrix of independent random numbers. Whenever a hole is created, the emulation will replace this random variable with a sum of random variables; for the first hole the variance of the emulated number will be a factor (N_G – 1)(N_R – 1) smaller than the simulation variance, or almost negligible. Ignoring interactions between holes, we get to the first order that the variance will be proportional to the number of holes, and hence the deviation will be the square root of that. For the direct mean, the deviation between the full and the reduced matrix mean will be (1/N–1/(N-m)) times the sum of existing simulations, plus 1/N times the sum of actual values of the holes. The variability of this can be reduced to m/(N(N-m)) times the single-simulation variability.

These dependence formulae are built on several assumptions. However, testing them on the actual data shows them to be very accurate to model the full curves for the actual analysis of Fig. 7 as a function of m with the form $A \sqrt{m/(N-m)}$ (Fig. 9). Also, the ratio between the two kinds of deviation depends on m as $1/\sqrt{(N-m)}$ as expected from this simple analysis (Fig. 10), though with a slight downward bend for the largest possible m.

Fig. 9

The simple-average curves of Fig. 7 for temperature, divided by $\sqrt{m/(N-m)}$. Full lines: Mean climate. Dashed lines: Climate change. DJF blue, MAM green, JJA orange, SON black

Fig. 10

The deviation ratio of Fig. 8 for temperature, divided by $\sqrt{N/(N-m)}$. Solid lines: Mean climate. Dashed lines: Climate change. DJF blue, MAM green, JJA orange, SON black

If we assume the functional form to hold for the real simulation matrix as a function of m, also for m = 1, we can straightforwardly calculate the mean deviation (D) between one-hole averages and true averages both for emulated and direct means, averaged over all one-hole configurations, and use the results to calculate proportionality factors. For simplicity of the equations below, we will ignore the scenario index (S) in these calculations and do it for the mean over scenarios; the results apply similarly to each scenario individually; for climate change, the RMS mean of the SGR term replaces the GR term in the formulae, SG and SR replace G and R. The results are:

$$ D_{emulated} \left( 1 \right) = \frac{{\sqrt {GR^{2} } }}{{\left( {N_{G} - 1} \right)\left( {N_{R} - 1} \right)}} $$

(4)

$$ D_{direct} \left( 1 \right) = \frac{{\sqrt {G^{2} + R^{2} + GR^{2} } }}{{\left( {N - 1} \right)}} $$

(5)

where the ANOVA terms correspond to the full matrix analysis, and where angled brackets indicate average over the matrix. Combining our approximations, we find the general formulae

$$ D_{emulated} \left( m \right) = \frac{{\sqrt {GR^{2} } }}{{\left( {N_{G} - 1} \right)\left( {N_{R} - 1} \right)}}\frac{{\sqrt {m } \left( {N - 1} \right)}}{N - m} $$

(6)

$$ D_{direct} \left( m \right) = \frac{{\sqrt {G^{2} + R^{2} + GR^{2} } }}{{\left( {N - 1} \right)}}\sqrt {\frac{{m \left( {N - 1} \right)}}{N - m}} $$

(7)

With these formulae we can, e.g., ask how large an improvement would be expected, using the slightly more complex emulated mean compared to the simple mean, provided that the goal is to be close to the total full-matrix mean. The ratio between the emulated and direct mean is

$$ \frac{{D_{emulated} \left( m \right)}}{{D_{direct} \left( m \right)}} = \sqrt {\frac{{GR^{2} }}{{G^{2} + R^{2} + GR^{2} }}} \frac{{\left( {N - 1} \right)^{3/2} }}{{\left( {N_{G} - 1} \right)\left( {N_{R} - 1} \right)\sqrt {N - m} }} $$

(8)

Remembering that the denominator in the square root is the total model variance for scenario means, we see that the expected improvement in estimating the total mean is directly proportional to the relative importance of the GR terms in the ANOVA analysis, i.e., how “well-behaved” the multi-model ensemble is towards being a sum of a GCM effect and an RCM effect (The G and R terms). The better behaved, the more reason to use an emulated estimate. The presence of noise at interannual to decadal scale will decrease the advantage of emulation, since individual simulations will be out of phase and therefore have relatively large individual GR values. These observations are reflected in the results of this study: Noisy fields like precipitation and wind, and especially extremes, have only a weak deterministic part, which can be described with the ANOVA terms, and have a large remaining noisy contribution to variability.

These formulae should work for each point and each season. In other words, it is possible to construct maps based on ANOVA parameters, which show the areas with the most likely improvement in results using emulation instead of direct averages. Of course, in a real-life situation with a given non-complete combination matrix, the full-matrix ANOVA parameters will have to be approximated from the parameters based on the emulation itself.

In Table 3 we show the ratio for m = 1 for the 4 seasons and five fields: average temperature, daily precipitation, and 10 m wind speed as well as the 10-year return value of daily precipitation and of maximum daily 10-m wind speed. In summary, the method is better suited for mean fields than for climate change; it is better for temperature and wind than for precipitation. There seems to be no systematic seasonal dependence, which is common for all fields. The error reduction, which is RMS averaged over points and over configurations, varies from a fourfold improvement for some temperature fields to a reduction of roughly one third for precipitation climate change.

Table 3 The ratio between emulated-mean and direct-mean deviation from full-matrix mean for one-hole matrix configurations for temperature, precipitation, 10 m wind speed, and 10-year return value of daily precipitation and of 10-m wind speed, for each season in per cent

For extreme precipitation and wind speed there seems to be no value at all using the emulation. According to Eq. 8, one missing simulation is the configuration where we expect the largest advantage of emulation, so we conclude that the spread between individual simulations due to climate variability, as manifested in the single-simulation GR and SGR terms, are too large for emulation to add value. In Fig. 11 we show the relative difference between the two deviations across Europe for winter averages of temperature, 10-m wind speed, precipitation, and 10-year return value of daily precipitation for configurations with a single missing simulation. It is clear that there is a large gain over the Atlantic Ocean for the averages, since this is very directly determined by the GCM with quite small variability; “GCM democracy” makes a relatively large difference in this case. For all seasonal-average fields, there is added value in all points with very few exceptions, using emulation instead of direct averaging. For the extreme case there are no areas with a systematic added value of the emulation technique at all. In this case, the individual simulation results at each individual point are influenced by internal variability, and the ANOVA analysis does not work well at all.

Fig. 11

Relative difference between emulated ensemble average deviation from true mean and direct ensemble average deviation from true mean, i.e., the relative improvement by using emulation instead of direct averages, for winter (DJF) precipitation change. Top panel: Seasonal average temperature. Second panel: Seasonal average 10-m wind speed. Third panel: Seasonal average precipitation. Bottom panel: 10-year return value of daily precipitation. Greenish colour means the emulation is worse than direct average

4 Conclusions

The current work focuses on a systematic investigation of effects of making a GCM-RCM matrix sparser and sparser. This allows for a quantification of how the emulation procedure deteriorates for more and more sparse matrices or, conversely, how much information may be gained by adding new simulations to existing sparse real-world simulation matrices compared to a filling with emulated values. Of course, we can only aim for an emulation of matrices, which are already partly populated; it is an additional challenge not addressed here to ascertain that the GCMs and RCMs in the matrix as far as possible are representative for larger multi-model ensembles. In situations where a well filled matrix is extended by addition of new simulations, e.g., a new GCM model downscaled by one or a few of the RCMs already in the matrix, the present technique can be used to fill in emulated values for the simulations with the new GCM not yet performed, and give an estimate of an ensemble average, where the new GCM has the same weight as the already present GCMs. It should be noted that the technique is linear and is unable to emulate effects of specific GCM-RCM combinations not in the matrix.

It turns out to be possible to get a general idea about the gains of using emulation to try to obtain a better ensemble average of a field with equal weighting of the participating GCMs directly from the full-matrix ANOVA parameters. This estimate does not specifically depend on the field in question, nor on season etc. It only depends on these through the values of the actual ANOVA parameters of the full matrix.

In a real-life situation, the combination matrix will be given, based on the actual simulations at hand. Averages based on emulation are expected to generally give better results than direct averages; based on the present analysis, the expected improvements can be estimated point by point and season by season from Eq. 8. The improvement is large when either the GCM or the RCM choice has a large influence on simulated results; it is smaller when the individual combination and/or inter-annual variability has a large influence compared to inter-simulation variability.

While the ANOVA-based hole filling technique works well when there is skill in the ANOVA contribution-splitting itself, our results for the 10-year precipitation return value shows that it does not work well when the ANOVA linear-term variabilities are much smaller than the total ensemble variability. This expected result is seen extremely clearly. The analytic formula for the two different ways of calculating the mean of an incomplete matrix shows that the ratio between emulated-matrix-mean error and direct-mean error is simply proportional to this term, for scenario mean matrices and for climate change matrices (not explicitly shown but exactly the same calculations).

A future perspective would be to investigate if it is possible to go beyond the current model-only world and learn something about biases. One obvious step would be to make a missing-simulation analysis of bias, i.e., investigating to which extent the biases of individual simulations can be written as the sum of a GCM-specific part and an RCM-specific part; Sørland et al. (2018) find that this is a problematic statement, and it would be interesting to investigate in the current very large ensemble. This would supplement the current analysis of mean fields and of climate change and also supplementing the evaluation of the entire ensemble performed by Vautard et al. (2020).

A further perspective, which will also be pursued in the future, is to put these results into perspective through further analyses of the role of internal variability, particularly of the GCM, in significance determination. Even when looking at 30-year averages, longer-time variations exist in GCM simulations, the details of which can be studied through downscaling of different ensemble members of the same GCM.

Appendix 1

In this appendix we will derive the expressions for ensemble averages in Eqs. 4 and 5, when there is exactly one simulation missing in a matrix. The ANOVA terms below will refer to their values for a complete matrix.

We will take each averaging method in turn. First the emulated mean (Eq. 4) in comparison to the complete-matrix average. The term D_emulated(1) is defined as the square root of the mean over configurations (hole positions) of the squared difference between the complete-matrix average and the emulated average.

In the derivation presented here, we will look at the average over periods to keep the equations manageable. We will use tildas for the situation with an incomplete matrix containing one emulated value, and non-tilda symbols for the full matrix. The derivation for each period proceeds in the same way, but has more terms. We let jk be the place with a missing simulation, and isolate $\tilde{Y}_{.jk.}$ from the equation $= 0$:

$$ GR_{jk} = 0 = \tilde{Y}_{.jk} - \widetilde{ Y}_{..k} - \widetilde{ Y}_{.j.} + \tilde{Y}_{ \ldots } = \tilde{Y}_{.jk} - Y_{..k } + \frac{1}{{N_{G} }}\left( {Y_{.jk } - \tilde{Y}_{.jk} } \right) - Y_{.j. } + \frac{1}{{N_{R} }}\left( {Y_{.jk} - \tilde{Y}_{.jk} } \right) + Y_{ \ldots } - \frac{1}{{N_{G} N_{R} }}\left( {Y_{.jk } - \tilde{Y}_{.jk} } \right) $$

which leads to

$$ \tilde{Y}_{.jk} = \left( {Y_{..k} + Y_{.j. } - Y_{ \ldots } - \left( {\frac{1}{{N_{G} }} + \frac{1}{{N_{R} }} - \frac{1}{{N_{G} N_{R} }}} \right)Y_{.jk } } \right)/\left( {1 - \frac{1}{{N_{G} }} - \frac{1}{{N_{R} }} + \frac{1}{{N_{G} N_{R} }}} \right) $$

We now calculate the difference in average between the complete matrix and the one with an emulated value. Since only the emulated place is different, we have the difference

$$ \frac{1}{{N_{G} N_{R} }}\left( {Y_{.jk } - \tilde{Y}_{.jk} } \right) = \frac{{\frac{1}{{N_{G} N_{R} }}\left( {Y_{..k. } + Y_{.j.. } - Y_{ \ldots . } - Y_{.jk. } } \right)}}{{\left( {1 - \frac{1}{{N_{G} }} - \frac{1}{{N_{R} }} + \frac{1}{{N_{G} N_{R} }}} \right)}} = \frac{{\frac{ - 1}{{N_{G} N_{R} }}GR_{jk} }}{{\left( {1 - \frac{1}{{N_{G} }} - \frac{1}{{N_{R} }} + \frac{1}{{N_{G} N_{R} }}} \right)}} $$

Taking the square, averaging over all jk and finally taking the square root leads to Eq. 4.

The second part is the difference between the direct averages of a full matrix and a matrix with one hole.

The direct average of the incomplete matrix can be written as

$$ \frac{{N_{G} N_{R} }}{{N_{G} N_{R} - 1}}\left( {Y_{ \ldots } - \frac{{Y_{.jk } }}{{N_{G} N_{R} }}} \right) $$

Therefore the difference in averages is

$$ \frac{1}{{N_{G} N_{R} - 1}}\left( {Y_{ \ldots } - Y_{.jk } } \right) $$

Squaring, averaging over jk and taking the square root leads to Eq. 5, noting that the complete spread of $Y_{.jk. }$ across the matrix by the ANOVA definitions is $G^{2} + R^{2} + GR^{2}$.