1 Introduction

Morocco is one of the Mediterranean and North African countries where observed global warming impacts are the most noticeable (Lelieveld et al. 2016; Sowers et al. 2011; Waha et al. 2017). Analysis of trends in precipitation and temperature in Morocco have indicated a tendency towards warmer and dryer conditions (Donat et al. 2014; Driouech et al. 2013, 2020a; Filahi et al., 2015; Sippel et al. 2017; Tramblay et al. 2013). Furthermore, most of the state-of-the-art models agree in projecting an increase in mean temperatures and a decrease in total annual precipitation amounts over the country (Driouech and El Rhaz 2017; IPCC, 2013, 2018; Polade et al. 2017), consistent with the whole Mediterranean region. Future changes in extremes are also expected, including increased drought and day and night-time extreme temperature events (Betts et al. 2018; Dosio and Panitz 2016; Giorgi et al. 2014; Molinié et al. 2018). Such changes would result in severe impacts on water resources, agriculture, and many other socio-economic sectors (Betts et al. 2018; Brouziyne et al. 2018; Döll et al. 2018; Driouech 2010; Marchane et al. 2017; Niang et al. 2014; Schewe et al. 2014; Tramblay et al. 2016; Wanders and Wada 2015). Moreover, the negative effects associated with climate change have been already witnessed in the past; i.e., drought leading to a drop in water reserves, agricultural productivity, and electricity generation (e.g., Verner et al. 2018). As a result, several efforts aimed at implementing appropriate adaptation actions and strategies have been undertaken.

To effectively plan adaptation to climate change, there is a need for detailed and precise information about the climate conditions that are expected for the future. In particular, the large uncertainty due to the choice of model is frequently pointed out by the adaptation community to be one of the main difficulties hindering the use of climate projections (e.g., Maraun et al. 2017; Sultan et al. 2020). Furthermore, there can be computational restrictions that, for some applications, impede the use of the full ensemble of models (e.g., Dalelane et al. 2018). Important efforts and accomplishments have been done by the scientific community to deliver reliable and actionable information on the relevant temporal and spatial scales. Our main tools for providing accurate estimates of future changes are global and regional climate models (GCMs and RCMs, respectively). Yet, uncertainty is an inherent feature of climate projections due to the chaotic nature of the climate system and the various assumptions the numerical models are subject to (e.g., the choice of emission scenario)(Blázquez and Nuñez 2013; Hawkins et al. 2016). Moreover, when working with ensembles, how to best handle model inter-dependencies becomes an important question to address since the contributing models are generally not designed to be independent of each other. Shared observational data for model tuning, common assumptions on the climate system as well as replication of code and shared components across different models(developed by independent institutions) result in similarities between the outputs (and correlation between the errors) of different models (Abramowitz et al. 2019; Annan and Hargreaves 2017; Eyring et al. 2019; Knutti et al. 2013; Sanderson et al. 2015a). Moreover, for several models, multiple realizations with slightly perturbed initial conditions (and therefore highly interdependent) are provided.

Model weighting approaches are used with the aim of reducing the unwanted uncertainty in climate model projections (Giorgi and Mearns 2003; Knutti et al. 2010; Murphy et al. 2004; Tebaldi and Knutti 2007). However, due to different model performances when compared to observations and the lack of independence among models, giving equal weight to each available model can be suboptimal (Boé et al. 2015; Eyring et al. 2019; Knutti et al. 2010). It is widely assumed that the reliability of a model in the future will come determined by its ability to reproduce the present-day climate (Hausfather et al. 2020). Consequently, some models would deserve more important weights than others in the construction of the multi-model ensemble depending on their performance for a given application (e.g., Baumberger et al. 2017; Eyring et al. 2019; Gleckler et al. 2008; Knutti et al. 2010, 2017). For instance, Cardoso et al. (2019) suggested a weighting method based on the models’ ability to represent spatio-temporal characteristics and PDFs of variables (e.g., the maximum and minimum temperature). More consistent/comprehensive weighting approaches account for both model performance and independence. Models that simulate the real world poorly as well as models duplicating other models are down-weighted (e.g., Brunner et al. 2019; Knutti et al. 2017; Lorenz et al. 2018). Dalelane et al. (2018) suggested using a weighting approach for the reduction of the number of ensemble members based on their performance and interdependencies with the objective of preserving relevant information on potential future climate states and maximizing the independent ensemble quality score.

Based on three widely used high-resolution datasets of climate projections (Euro-CORDEX, bias-adjusted Euro-CORDEX, and NEXGDDP), this study evaluates the effect of three different multi-model combination strategies (simple averaging, model weighting based on model performance, and model weighting based on model performance and independence) on the climate changes projected over northern Morocco for the end of the twenty-first century and under two different emission scenarios (RCP4.5 and RCP8.5). In particular, we focus not only on temperature and precipitation, but also on a number of related extreme indices for 22 local stations. Note that, to the authors’ knowledge, this is the first attempt to undertake such a comprehensive analysis on the advantages and limitations of different multi-model combination approaches for this region.

The paper is structured as follows: in Sect. 2, we describe the data, the weighting methods, and the climate indices used. The results are presented and discussed throughout Sects. 3 and 4. Finally, the main conclusions are delineated in Sect. 5.

2 Data and methods

2.1 Observed data

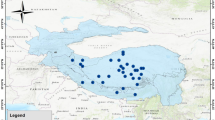
Morocco is located in the Northwest of the African continent, extending from 21 to 37°N and bordering the Mediterranean Sea in the north and the Atlantic Ocean in the West. Moroccan climate is influenced by the Atlantic Ocean, the Mediterranean Sea, and the Sahara (Knippertz et al. 2003; Born et al. 2008; Driouech et al. 2009; Tramblay et al. 2012) leading to a sub-humid to semi-arid climate in the north and an arid to desertic climate in the south. Observed daily precipitation, maximum and minimum temperature time series collected at 22 Moroccan meteorological stations are used in this study (Fig. 1) to compute the different weights that are applied to each model based on its ability to reproduce the observed historical climate. These data have been provided by the Moroccan National Meteorological Service (La Direction Générale de la Météorologie) and cover the period 1971–2005. The days with missing values (less than 0.5% of the available data) were omitted from the analysis. The geographic distribution of the 22 stations covers the main climate regions excluding the south (Hamly et al. 1998; Knippertz et al. 2003; Ward et al. 1999). In fact, we limit the analysis to the northern half of the country due to the common domain covered by the three ensembles used (see Sect. 2.2). In particular, the Euro-CORDEX project doesn’t cover the whole country (see Fig. 1) and some stations were excluded to avoid undesired border effects. Nevertheless, note that our target region corresponds to the wettest part of the country.

Fig. 1
figure 1

Geographical distribution of the 22 stations used in this work. The size of the circles indicates the length of the available records. The map at the bottom-right corner shows the Euro-CORDEX domain (light shading)

Full size image

2.2 Modeled data

To assess the effect of model weighting on present-day climate and future climate change estimates, we use, for the first time, data from three state-of-the-art multi-model ensembles: the NASA Earth Exchange Global Daily Downscaled Climate Projections (NEXGDDP), Euro-CORDEX, and bias-adjusted Euro-CORDEX ensembles. In particular, we use daily maximum temperature, minimum temperature, and precipitation issued from the first member (first run r1i1p1) of each ensemble.

The NEXGDDP dataset consists of 21 General Circulation Model (GCM) from the Coupled Model Intercomparison Project Phase 5 (CMIP5, (Taylor et al. 2012)), which have been statistically downscaled to a global grid generated using the Bias-Correction Spatial Disaggregation (BCSD) method (Maraun et al., 2017; Thrasher et al. 2012; Wood et al. 2004) on a global grid with a spatial resolution of 0.25°. Table S1 in the supplementary material provides the list of the 21 models included in the NEX-GDDP dataset. Data access, as well as detailed documentation about NEX-GGDP, are available at https://www.nccs.nasa.gov/services/data-collections/land-based-products/nex-gddp.

The Euro-CORDEX dataset (Jacob et al. 2014) contains daily information at a spatial resolution of 0.11º from several Regional Climate Models (RCMs) which have been driven by multiple GCMs from CMIP5. In addition, to assess the potential added value of bias adjustment over the raw RCM outputs, we also use the bias-adjusted Euro-CORDEX dataset. Note that it is widely recognized that climate model outputs should not be used directly as inputs for impact models and some kind of adjustment towards the observed climatology is necessary (Manzanas et al. 2019). For consistency, notice that only the 10 GCM-RCM combinations which are simultaneously available in both the raw and the bias-adjusted Euro-CORDEX datasets were used for this work (see Tables S2 and S3), which can be retrieved from the ESGF portal (https://esgf-node.ipsl.upmc.fr/projects/esgf-ipsl/).

For all the three multi-model ensembles used, we consider 1971–2005 as the historical reference period. Future changes are analyzed for the period 2071–2100 (with respect to 1971–2005). Two Representative Concentration Pathways (RCP) scenarios, RCP4.5 and RCP8.5, were considered (Moss et al. 2010; van Vuuren et al. 2011). RCP4.5 assumes a radiative forcing increase of 4.5 W/m2 by the end of the century, relative to the pre-industrial era, associated with a peek of global emissions around 2040 and its stabilization until 2100. RCP8.5 assumes that emissions rise throughout the twenty-first century leading to a radiative forcing of 8.5 W/m2 by the end of the century, relative to the pre-industrial era (Riahi et al. 2011).

2.3 Model weighting

We compare three different combination approaches to form suitable multi-model ensembles, ranging from the most straightforward arithmetic average of models to more sophisticated alternatives which take into account the models’ performance and interdependence. Each of these combination approaches/weighting methods is applied to both historical and future climate simulations issued from the three ensemble datasets (NEXGDDP, Euro-CORDEX and bias-adjusted Euro-CORDEX). A multi-model ensemble average (m) can be calculated as follows:

$$m=\frac{{w}_{i}*{m}_{i}+\dots +{w}_{N}*{m}_{N}}{N}$$
(1)

where \({m}_{i}\) are the individual models’ values, \({w}_{i}\) the correspondent weight for model i and N the number of models in the ensemble.

The first combination approach (MM-AVG in the following) consists of calculating the multi-model ensemble average as an arithmetic mean which supposes equal weights for all contributing models, \({w}_{i}\)=\({w}_{N}=1\).

The second approach (MM-PERF hereafter) is based on models’ performance and calculates weights based on metrics rankings (Cardoso et al. 2019). Models that agree well with the selected set of observations get high weights and vice versa (see Sect. 2.3.1 for details).

The third approach (MM-PERF + I hereafter) accounts for both model performance and independence (Knutti et al. 2017). Models that have poor performance get less weight and models that largely duplicate existing models (inter-dependent models) also get less weight (detailed in Sect. 2.3.2).

Weights are calculated over the historical period (1971–2005) at the annual scale, for each climate variable/indicator (see Sect. 2.4) at each of the 22 stations considering their nearest neighbors in the models’ grids.

2.3.1 The MM-PERF method

The MM-PERF method focuses on the model's historical run quality. Four validation metrics are computed for each climate variable/indicator (precipitation, temperature, and related extreme indices) by model and station. The mean bias, the root mean square error (RMSE), the normalized standard deviation ratio (\(\sigma\)), and the Pearson correlation (r) are calculated between the model and the observations (Cardoso et al. 2019; Soares et al. 2017). Then, a ranking of models is built based on these metrics by introducing specific ranks (Cardoso et al. 2019). A model with higher performance is a model with higher metrics’ ranks and therefore gets a higher weight.

Let’s consider n as the number of observed/modeled timesteps, N as the number of models in each ensemble, o and p the observation and model values respectively, and ō and p̄ the corresponding means calculated over the historical period.

For the first two metrics (bias and RMSE), ranks are equal to the inverse of the absolute value since the best expected result should be closest to zero (Eqs. 2 and 3). As the optimal value for normalized standard deviation is 1 and since in some cases the deviations are very small, the normalized standard deviation ratio rank is its inverse in case of values superior to 1 (Eq. 4). The correlation related rank is calculated by adding 1 to the correlation value in order to prevent negative ranks (5).

$${Bias}_{rank}=\frac{1}{\left|\sqrt{\frac{1}{n}{\sum }_{k=1}^{n}({p}_{k}-{o}_{k})}\right|}$$
(2)
$${RMSE}_{rank}=\frac{1}{\left|\sqrt{\frac{1}{n}{\sum }_{k=1}^{n}{({p}_{k}-{o}_{k})}^{2}}\right|}$$
(3)
$${\sigma }_{rank}=\sigma =\frac{{\sigma }_{p}}{{\sigma }_{o}}=\frac{\sqrt{\frac{1}{n}{\sum }_{k=1}^{n}{({p}_{k}-\overline{p })}^{2}}}{\sqrt{\frac{1}{n}{\sum }_{k=1}^{n}{({o}_{k}-\overline{o })}^{2}}} if\sigma <1 ; \frac{1}{\sigma } if \sigma >1$$
(4)
$${r}_{rank}=1+\frac{{\sum }_{k=1}^{n}\left({o}_{k}-\overline{o }\right)-({p}_{k}-\overline{p })}{\sqrt{{\sum }_{k=1}^{n}{({o}_{k}-\overline{o })}^{2}{\sum }_{k=1}^{n}{({p}_{k}-\overline{p })}^{2}}}$$
(5)
$$rank=\frac{{rank}_{i}}{{\sum }_{j\ne i}^{N}{rank}_{j}}$$
(6)
$${w}_{i}=\frac{w(i)}{{\sum }_{j\ne i}^{N}w(j)}$$
(7)

Ranks are then normalized by dividing each value by the sum of all ranks of other models in a way to have the total sum of the ranks for each metric equal to 1. (6).

Weights w(i) are computed by averaging the ranks of the four metrics. And finally, each weight is normalized so that the sum of the weights (\({w}_{i}\)) in the ensemble is equal to 1. (7).

2.3.2 The MM-PERF + I method

The MM-PERF + I weighting scheme extends the previous method by additionally considering model interdependence. It takes into account both model quality and uniqueness. Models that agree well with observations for the selected set of diagnostics get high weight and models that show uniqueness (do not duplicate existing models) compared to other models in the ensemble get also high weight (Knutti et al. 2017; Lorenz et al. 2018; Sanderson et al. 2015a, b). The weighting first requires defining a distance metric Di of model i to observations, and \({S}_{ij}\), the distance metric between model i and model j, and a relationship to convert those into a weight.

We use the Euclidean distance as a metric to quantify the distances between model simulations and between model simulations and observation as in (Sanderson et al. 2015a).

For M models in each ensemble, the single model weight \({w}_{i}\) for model i is defined as follows:

$${w}_{i}=\frac{{e}^{\frac{{{D}_{i}}^{2}}{{{\sigma }_{D}}^{2}}}}{1+{\sum }_{j\ne i}^{M}{e}^{-\frac{{{S}_{ij}}^{2}}{{{\sigma }_{S}}^{2}}}}$$
(8)

The numerator represents model skill by using a Gaussian weighting where the weight decreases exponentially the further away a model is from observations.

The denominator is the “effective repetitionradia of a model” and is intended to account for model interdependency (Knutti et al. 2017; Sanderson et al. 2015a, 2015b). If a model has no close neighbors, then all \({S}_{ij}\) (i ≠ j) are large, the denominator is approximately one and has no effect. If two models i and j are identical, then \({S}_{ij}\) is null and the denominator equals two, so each model gets half the weight. The constants \({\sigma }_{D}\) and \({\sigma }_{S}\) determine how strongly the model performance and similarity are weighted, large values will lead to an approximation of equal weighting while very small values will lead to aggressive weighting and possibly overconfident results (Knutti et al. 2017; Lorenz et al. 2018). The distance \({\sigma }_{S}\) is also called ‘‘radius of similarity” and is used to adjust the (nonlinear) decrease of the exponential function to the desired range of distances, we chose here the mean distance between simulations as in Dalelane et al. (2018). The quantity \({\sigma }_{D}\) is an analog to \({\sigma }_{S}\) determining how strongly the model’s error is penalized, for which we use here the mean distance between simulations and observations. The weights are finally normalized so that their sum equals one.

2.4 Extreme indices

In addition to annual mean temperature and precipitation, we considered a set of four climate extreme indices to assess the effect of weighting. The daily mean temperatures are calculated as the sum of the daily minimum and maximum temperatures divided by two. The four extreme indices used here are defined in the ETCCDI (Frich et al. 2002; Peterson et al., 2002; Zhang et al. 2011) and are linked to high precipitation events (R95p), drought (CDD), heat waves (WSDI) and cold waves (CSDI) (see Table 1). Mean temperature and precipitation as well as climate extreme indices are calculated at an annual scale for the historical period (1971–2005) and the future period (2071–2100) under the two RCP scenarios (RCP4.5 and RCP8.5). For WSDI (CSDI), the 90th (10th) percentile is computed independently for each day of the year (e.g., 18 of June) based on a 5-day running window surrounding that day during 1971–2005. The latter is also the baseline period considered to compute the 95th percentile for the case of the R95p indicator. Note that projected changes (Sect. 3.2) for any of these three indicators are computed with respect to the percentile values obtained for 1971–2005.

Table 1 List of the extreme indices used with their acronyms, full name, definition, and corresponding units
Full size table

3 Results

3.1 Assessment of models’ historical runs

Evaluating the quality of climate models over the historical period is key to understanding the reliability of the climate change responses. Since this study aims at assessing the effect of model weighting, this section compares unweighted and weighted models from the three multi-model ensembles considered and does not evaluate or compare the different GCMs/RCMs individually. For each climate indicator (mean temperature, mean precipitation, and related extreme indices), Fig. 2 shows the mean biases along the 22 stations of interest (for which the nearest model grid box is considered). The results obtained from the individual models are shown by blue boxplots. The boxplots assigned to each of the multi-model ensembles’ means are obtained using the three different weighting methods respectively (MM-AVG: orange, MM-PERF: green, and MM-PERF + I: pink). Note therefore that whereas the blue boxplots contain 22 × N values (N is the number of individual models), the remaining boxplots (orange, green, and pink) contain only 22 values (one for each station, as given by the corresponding multi-model ensemble mean). This allows analyzing the multi-models’ uncertainty range before and after weighting as well as the effect of weighting on the ensemble’s performance.

Fig. 2
figure 2

Boxplots for biases of mean temperature (°C) (a), cold (CSDI) (b) and warm (WSDI) (c) spells (days) indices, as well as biases of mean precipitation (mm/day) (d), high precipitation (R95P) (mm/day) (e) and drought (CDD) (days) (f) indices. Biases for unweighted individual models (blue) and weighted models (orange, green, and pink) are obtained per comparison to stations’ observations over the period 1971–2005. The number above each non-blue boxplot is the percentage of \({sd}_{ratio}\) higher than one (see the text for details)

Full size image

A new metric (\({sd}_{ratio}\)) is included to assess whether the reduction in spread exhibited by the non-blue boxplots is a consequence of the weighting process or a simple reduction in the sample size. For each individual model (in each blue boxplot), we compute the standard deviation (\({sd}_{i}\), i varying from 1 to N) along the 22 stations. Then, we compute the ratios between these \({sd}_{i}\) values and the standard deviation obtained from each of the non-blue boxplots (\({sd}_{m})\).

For each model i, the standard deviation ratio (\({sd}_{ratio}\)) is given as follows:

$${sd}_{ratio}\left(model\right)=\frac{{sd}_{i}}{{sd}_{m}}$$
(9)

A ratio higher than 1 would indicate that the standard deviation of the particular model is higher than the one issued from the weighted multi-model mean. Finally, for each weighting approach, we compute the percentage of ratios exceeding 1. The same procedure is also conducted for future changes’ boxplots (Figs. 3 and 5) in Sect. 3.2.

Fig. 3
figure 3

Boxplots of future changes for mean temperature (°C) (a, d), CSDI (days), (b, e) and WSDI (days) (c, f) for the period 2071–2100, with respect to 1971–2005. Results for the RCP4.5 (RCP8.5) scenario are shown in the top (bottom) row. The number above over each non-blue boxplot is the percentage of \({sd}_{ratio}\) higher than one (see the text for details)

Full size image

In order to investigate whether the effect of weighting is smoothed by the combination of all stations together, annual evolution curves comparing observations, individual models, and weighted multi-model ensembles are also analyzed at local stations. These curves (Figs. S2–S6) reflect the same conclusions extracted from the boxplots, indicating that the three weighting approaches yield similar results even at a local scale.

3.1.1 Temperature and related extreme events

The bias values of unweighted models show that the bias-adjusted Euro-CORDEX ensemble performs, as expected, relatively well in reproducing annual mean temperatures at the local scale despite some overestimations with a median bias of about 0.5 °C (Fig. 2a). Residual biases are more important in the case of NEXGDDP which tends to underestimate the mean temperature. This is probably due to differences between the observational gridded datasets that have been used as a reference for bias correction in the two ensembles (Landelius et al. 2016; Maurer and Hidalgo 2008; Thrasher et al. 2012; Wood et al. 2004) and the local observations used in this work. Cases of important differences between observational datasets for particular regions have been in fact highlighted by previous studies (Herrera et al. 019; Kotlarski et al. 2017; Manzanas et al. 2020). The weighting effect is more noticeable in the Euro-CORDEX ensemble case, with an improvement of the overall performance and a median bias reduced from − 1 °C to around − 0.5 °C. Based on the interquartile range of boxplots, a considerable reduction of the spread of local biases for the two dynamically downscaled ensembles is also noticed. Overall, the three weighting methods have almost the same impact for each of the three ensembles (orange, green, and pink boxplots). Weighting produces the smallest effect in the case of NEXGDDP, for which higher biases (compared to the other ensembles) are found. Note that important biases exhibited by NEXGDDP when compared to local data have also been found in previous studies (e.g., Chen et al. 2020). These biases may be related to inherent limitations of the bias correction approach used to generate this database, as bias correction techniques may present serious drawbacks when the gap between the spatial resolution of models and observations is large (Maraun et al. 2017). To cope with this issue, the latter study also advocated the development of new methods combining advanced statistical modeling with physical understanding (Addor et al. 2016; Volosciuk et al. 2017).

The biases for cold and warm spell duration indices (WSDI and CSDI) are shown in (Fig. 2b, c, respectively). All multi-model ensembles tend to overestimate the numbers of extreme temperature events, with median biases slightly higher for warm spells. The weighting effect is obvious in terms of reducing the spread of the biases but also provides a slight improvement of the overall quality of ensembles. In particular, the MM-PERF method leads to relatively smaller median biases compared to the other weighting methods. An exception is found for NEXGDDP, which shows a smaller and comparable effect between the weighting methods in the case of WSDI.

3.1.2 Precipitation and related extreme events

As for temperature related indices, the three weighting methods lead in general to similar results for each ensemble for both mean precipitation and precipitation extreme events (R95p and CDD). In particular, the biases’ mean value and dispersion are reduced (Fig. 2d, e, f respectively). An exception comes from Euro-CORDEX, for which MM-AVG and MM-PERF + I exhibit relatively lower biases in the case of mean precipitation and the drought index respectively. An overall improvement of the simulated values is noted in the case of dynamically downscaled data. Such improvement is however more noticeable for uncorrected simulations.

We also note a better performance of bias-adjusted Euro-CORDEX simulations for both mean and extreme precipitation events. This added value is however overtaken by the weighting in the case of extreme events. Although the improvements resulting from the application of weighting, Euro-CORDEX multi-model mean, in agreement with previous studies, underestimates annual mean precipitation (Vaittinada Ayar et al. 2016; Zittis et al. 2019) and the length of the longest annual dry period. The drought index is also underestimated by the bias-adjusted Euro-CORDEX ensemble and on the contrary overestimated by NEXGDDP. Contrasted biases are given for the high precipitation index.

For both precipitation and temperature indicators and in the majority of the cases, the percentages of \({sd}_{ratio}\) higher than one are clearly above 50%, which confirms that weighting contributes efficiently to reducing the spread of the biases shown by the individual models.

3.2 Assessment of future changes

Projected changes for temperature and precipitation and their related extreme indices (CSDI, WSDI, R95p, and CDD) are analyzed in this section under the two emission scenarios considered (RCP4.5 and RCP8.5) for 2071–2100, with respect to the historical period 1971–2005. In particular, we analyze the distribution of the changes for both the unweighted individual models and the weighted multi-model ensemble means obtained from the MM-AVG, MM-PERF, and MM-PERF + I methods (Figs. 3 and 5), which allows for a better understanding of the effect of weighting on the uncertainty of the future projections. In addition, for the particular case of the weighted bias-adjusted Euro-CORDEX ensemble, which was found to provide the best performance in present climate conditions (see Fig. 2), we also look at the spatial patterns of the projected changes (Fig. 4). For each indicator, the Mann–Whitney U test has been applied to test the statistical significance (at a 95% confidence level) of the change at the station level. Note that the Mann–Whitney U is non-parametric and does not make any assumption about the distribution of the underlying data (James and Washington 2013).

Fig. 4
figure 4

Future changes of mean temperature (°C) (a), CSDI (days) (b), WSDI (days) (c), precipitation (%) (d), R95p (%) (e) and CDD (days) (f) obtained from weighted bias-adjusted Euro-CORDEX multi-model ensemble according to RCP8.5 for the period 2071–2100, with respect to 1971–2005. Within each panel, top/middle/bottom maps correspond to the MM-AVG/MM-PERF/MM-PERF + I weighting method. A black circle indicates that the projected change is significant at a 95% confidence level, according to a Mann–Whitney U test

Full size image

3.2.1 Temperature and related extreme events

The boxplots in Fig. 3 show the spread of the projected changes for annual mean temperature along the 22 stations, as projected under the RCP4.5 and RCP8.5 scenarios (panels a and d, respectively). The three ensembles of models project a generalized increase in temperature by the end of the century. Warming varies between 1.5 °C and 3 °C (3.5 ºC and 5 ºC) according to RCP4.5 (RCP8.5), depending on the model and location, which is in agreement with previous studies (Donat et al. 2013; Filahi et al. 2015; Ozturk et al. 2018; Waha et al. 2017; Zittis et al., 2019). Note that weighting shows a better performance in reducing uncertainty for the bias-adjusted Euro-Cordex and NEXGDDP ensembles (with higher percentages of \({sd}_{ratio}\) higher than one). Moreover, in some cases, weighting can introduce slight changes in the signals projected by the unweighted ensemble mean. For instance, the median change corresponding to the three weighting methods is shifted up (compared to the individual models’ median), which indicates that higher weights are given to the models that reproduce higher warming levels. Note the importance of this result which suggests that weighting would contribute to the provision of more reliable future climate information (e.g., Brunner et al. 2019). This is also reflected in the mean temperature evolution curves (see Fig. S5) where the weighted multi-model curves are shifted up compared to the median curve of the individual models at local stations.

Projected changes for CSDI are shown in the boxplots in Fig. 3b, e. Overall, the projected signals from the three ensembles are similar, although NEXGDDP tends to project higher reductions for both scenarios. Changes vary from + 1 to − 7 days for RCP4.5(+ 1 to − 9 days for RCP8.5). Most of the models don’t project any cold spells by the end of the century, which might be related to significant projected increases in yearly mean minimum temperatures.

The difference between the three weighting methods is clearer for NEXGDDP. Indeed, MM-PERF and MM-PERF + I methods project higher changes than MM-AVG for which the median change is close to the individual models’ median change, indicating that higher weights are given to the NEXGDDP models projecting higher decreases. This is more noticeable for the Warm Spell Duration Index (WSDI), shown in Fig. 3c, f, and confirms that higher weights are given to warmer models. This is also noticeable from the curves showing the annual evolution (Fig. S6) and corroborates that weighting seems to be more sensitive to the climate index than to the spatial location. This can be explained by the fact that individual models perform better for some indicators than for others, which results in a different weighting effect (more noticeable for indicators poorly simulated by the models, e.g., WSDI here). Moreover, the low spatial variability of the results obtained may be presumably related to the relatively small size of our target region, which might explain the similar weighting effect found across the different stations.

Changes’ variation for WSDI is larger than for CSDI (Fig. 3b, e) and we can notice higher amplitudes for WSDI, suggesting that the warming will gain more from high temperature events than cold ones, consistent with observed trends in Driouech et al. (2020a). Changes’ amplitudes are even higher for NEXGDDP. Indeed, for RCP4.5 (RCP8.5), the Euro-CORDEX ensemble projects increases up to 150 (250) days while increases of more than 200 (300) days are expected according to NEXGDDP models. Remarkably, the spread of the projected changes, which is the highest for NEXGDDP, is largely reduced after weighting.

For a spatial assessment of these results, maps in Fig. 4a show for the 22 locations of interest, the projected changes for annual mean temperature, as given by the weighted bias-adjusted Euro-CORDEX ensemble under the RCP8.5. In general, the yearly mean temperature is expected to increase significantly over Morocco in the range between 4 and 5.5 °C in inland stations and between 2.5 °C to above 3.5 °C near the coast. The MM-PERF + I method shows slightly different results in a few stations while the MM-AVG and MM-PERF give similar spatial patterns of changes. The increase is statistically significant at a 95% level over nearly all stations for both scenarios RCP4.5 and RCP8.5. The pattern of changes is mostly linked to inland/coastal contrast and is also noticed for the RCP4.5 scenario (see Fig. S1.a). Similar results about cooler mean temperature changes near coasts were discussed in Cardoso et al. (2019) focusing on Portugal. The lower warming in the coastal areas may be related to local sea-breeze circulations responsible for the transport of cooler and moisture air, hence softening the effects of climate change local warming.

As for CSDI and WSDI indices, the spatial pattern of projected changes across the 22 stations considered is shown in (Fig. 4b, c respectively). The changes for both indices are statistically significant in most of the stations. CSDI is expected to decrease down to 5 days, especially in inland stations. WSDI, however, is expected to increase substantially: up to 100 days in coastal regions and between 100 and 200 days in inland regions. This means that, by the end of the century, between one and two thirds of the year would correspond to what’s currently considered a heatwave spell. Doubtless, this will have important effects on different socio-economic sectors, including agriculture, health, tourism, etc.

3.2.2 Precipitation and related extreme events

The boxplots for projected annual precipitation changes over Morocco are shown in Fig. 5a, d. Our results indicate a high consensus between models in all ensembles towards a decrease in annual precipitation, which is in agreement with previous studies (Thrasher et al., 2012; Driouech et al. 2013, 2020b; Tramblay et al. 2013; Donat et al. 2014). Some individual models from bias-adjusted Euro-CORDEX and NEXGDDP project an increase of about 10% for the RCP4.5 scenario. Comparing the three ensembles, Euro-CORDEX projects the highest decreases, with changes ranging from about − 20% to − 40% under RCP4.5 (− 35% to − 55% for RCP8.5). For the other two ensembles, the projected changes for RCP4.5 are 5%–10% lower. The three weighting methods further reduce such differences in the strength of the decrease, leading all of them to very similar results within each ensemble. The weighting contributes highly to reducing the uncertainty of precipitation changes across the different stations (orange, green, and pink boxplots of Fig. 5a, d). Indeed, the standard deviation of the results found for the three multi-model means is much smaller than individual models, regardless of the weighting approach considered.

Fig. 5
figure 5

Boxplots of future changes for precipitation (%) (a, d), R95p (%) (b, e) and CDD (days) (c, f) for the period 2071–2100, with respect to 1971–2005. Results for the RCP4.5 (RCP8.5) scenario are shown in the top (bottom) row. The number above over each non-blue boxplot is the percentage of \({sd}_{ratio}\) higher than one (see the text for details)

Full size image

A similar weighting effect is also noticeable for high precipitation events (R95p) and annual longest dry spell (CDD) despite the projected changes are intensified by MM-PERF and MM-PERF + I for the case of NEXGDDP (Fig. 5b, c, e, f). In general, a decrease in the percentage of precipitation amounts issued from very wet days can be expected from all ensembles for both scenarios although some individual models project increases up to 20%. The decrease in R95p varies mostly, for individual models, between + 40 and − 80% for RCP4.5 and between + 20 and − 100%, for RCP8.5. Weighting leads to median changes around − 20% for both Euro-CORDEX ensembles for RCP4.5 and around − 45% for RCP8.5 independently from the method used. MM-PERF and MM-PERF + I project a 5% more decrease in annual precipitation from very wet days for NEXGDDP. Consistent with the projected reductions in precipitation across the stations, all ensembles project an increase in the number of CDD, indicating that more prolonged drought episodes are expected in the future. The changes issued from individual models range between − 10 and 50 days for the RCP4.5 scenario and between − 10 and 80 days for RCP8.5. NEXGDDP ensemble projects the lowest increase although the spread amongst models is reduced by the weighting and the additional few days gained from MM-PERF and MM-PERF + I methods respectively.

Maps in Fig. 4d, e, f show the spatial patterns of projected changes for precipitation and its related extreme indices. These maps bring to light a general and statistically significant decrease in both mean and extreme precipitation, together with a reinforcement in drought persistence. In particular, projected changes for high precipitation events (R95p) are more significant in the case of RCP8.5 than for RCP4.5 (see S1). For all the ensembles, the three weighting methods lead to similar projected changes. Very few stations (2–3) exhibit some slight increase or decrease in the amplitude of the projected changes depending on the method and index.

4 Discussion

Finding the ideal solution for climate model weighting has been controversial so far. Indeed, beyond the question of whether or not to weigh the different models, the metrics and methods used for this task have been largely discussed in the literature, and advantages, as well as limitations, have been found depending on the application of interest. In principle, it seems reasonable to think that weighting models according to their performance and interdependence may ensure ensemble democracy (Knutti et al. 2017). Thus, one of the aims of this work is to confirm whether or not more sophisticated weighting procedures based on model performance and independence outperform simpler ones based only on model performance, and to compare both alternatives with straightforward averaging (i.e., equal weights). The choice of metrics for both first approaches, the size of each ensemble as well as the chosen time scale constitute the main limitations of this work.

There are multiple ways to proceed with model weighting and it is very difficult to agree on an optimal way. An infinite number of performance metrics can be defined: quality assessment metrics such as correlation, root mean square error, and bias for example (Baumberger et al., 2017 and Cardoso et al. 2019), spatial performance assessment metrics such as SPAtial EFficiency metric (SPAEF) or Fractions skill score (FSS) (Ahmed et al. 2019; Koch et al. 2018) or any other quality scores comparing the model to observations. However, the choice of an appropriate performance metric is quite challenging (Keupp et al. 2019; Knutti et al. 2010, 2018; Weigel et al. 2010).

Moreover, weighting approaches can be very sensitive to the chosen metric: if weighting is based on a criterion that is inadequate for the targeted quantity or is dominated by variability, then there is a possibility that the result gets worse rather than better (Weigel et al. 2010). The performance metrics considered for this work have been selected based on similar previous studies but other metrics might have led to different weights and ranks and therefore to maybe different results (e.g., Gleckler et al. 2008; Kjellström et al. 2010; Ring et al. 2017).

The sensitivity to the metric choice can also depend on the number of the models considered (Knutti 2018). Hence, the differences we noticed between NEXGDDP and Euro-CORDEX datasets could be more related to the size of the corresponding ensembles (21 and 10, respectively) than to the different nature (statically and dynamically downscaled, respectively). Some studies select the best performing models to constitute new “smaller” sub-ensembles (Ahmed et al. 2019; Cardoso et al. 2019). This would definitely give different results for the three weighting approaches considered in this work. However, it can lead to the loss of information from the eliminated models. It can also induce some political sensitivities since it is difficult to dismiss models from certain centers or countries in a coordinated modeling project for example.

As an alternative to assigning weights to models, another research topic focuses on the so-called emergent constraints which allow for reducing the uncertainties in climate change projections through a relationship between the observation and the projection (Wenzel et al. 2014). This relationship (usually established through some form of regression across models) can then be used to estimate a constrained projection that is relatively independent of the underlying models (Boé et al. 2009; Cox et al. 2013; Mahlstein et al. 2012). This method is, however, highly susceptible to the quality of the observed data, the understanding of the physical processes, and sometimes the subjective decisions of the researcher (Keupp et al. 2019). As shown in Caldwell et al. (2018), recent studies using emergent constraints on equilibrium climate sensitivity have pointed out several limitations of this method. Other options consist of interpolations in a low-dimensional model space (Sanderson et al. 2015b) or Bayesian methods (Tebaldi et al. 2004).

Our results add evidence to the statement by Weigel et al. (2010) that equal weighting, for some applications, maybe the most transparent way to combine models and can be preferable to other weighting strategies which may not represent the true hidden uncertainties appropriately. Furthermore, a simple evaluation of models’ performance for the present climate is not really sufficient to rank the ‘best performing’ models (e.g., Dosio et al. 2019). Thus, it is challenging to find a suitable methodology to subsample an ensemble by just weighting-based approaches. We also found that taking the independence of models within the ensemble into consideration may not be of much help in some applications, especially when this aspect is evaluated based on the same kind of metrics used to evaluate the models’ performance.

All this implies that efficient model weighting requires a more careful investigation of models’ performance and independence by taking into account the ability of the models to simulate the physical driving processes which are key for the region and application of interest.

5 Conclusion

We investigate in this work the effect of model weighting over a collection of widely used multi-model ensembles -Euro-CORDEX, bias-adjusted Euro-CORDEX, and NEXGDDP- over northern Morocco. We apply three different weighting methods of reference nowadays and use 6 climate indices: mean temperature, CSDI, WSDI, mean precipitation, R95P, and CDD. All model simulations were first evaluated against local observations issued from a set of 22 meteorological stations for the historical period (1971–2005).

Our results show that weighted ensembles provide better scales than unweighted ones. In particular, weighting is useful in centering the model simulations towards the observed quantities and reducing their biases’ mean value and dispersion. This suggests that weighted ensembles may provide more reliable (i.e., less uncertain) future projections in the climate change context.

None of the three weighting approaches is found to be systematically better than the others; they provide similar results in most of the cases. The bias-adjusted Euro-CORDEX ensemble shows the smallest bias for mean temperature but a similar weighted median bias (compared to the two other multi-model ensembles) for warm (WSDI) and cold extreme events (CSDI). The bias-adjusted Euro-CORDEX exhibits also the smallest bias for mean precipitation and its related extreme indices (CDD and R95p). Our results indicate also a better performance of dynamical downscaling (i.e., Euro-CORDEX) with respect to global bias-corrected datasets (i.e., NEXGDDP), in particular for the reproduction of extreme indicators at the local scale. Nevertheless, it is important to remark that the raw Euro-CORDEX simulations also present their own biases (large in some cases), requiring thus the posterior application of bias correction or other more advanced post-processing. Furthermore, the results highlight that even bias-corrected datasets (bias-adjusted Euro-CORDEX and NEXGDDP) still show biases when compared to local observations. This highlights the issue of uncertainty linked to observational datasets as well as the fact that the bias correction effect depends on the method, the parameter, and the scale.

Future changes of the six climate indicators considered were also investigated under two emission scenarios (RCP4.5 and RCP8.5). Our results show that all models project a significant temperature increase over Morocco, more severe in inland regions than near coasts for both scenarios. Moreover, the vast majority of the models suggest an increase of warm spell durations by the end of the century while cold spells are not expected. Besides, most of the models agree on an alarming decrease in precipitation and accordingly longer and more severe dry conditions. Based on the multi-model mean changes, most of the models show a decrease in the amount of precipitation issued from high precipitation events although some individual models project an increase.

A difference between the three weighting approaches is found for the NEXGDDP ensemble in the case of extreme indices, especially WSDI and CDD. MM-PERF and MM-PERF + I tend to project more severe changes (less precipitation and higher warming) highlighting the fact that more warming/drying models are given higher weights (these models are considered more reliable). For the other indicators, the uncertainty due to the choice of the multi-model combination strategy is nearly negligible, with the three weighting methods leading to almost identical spatial patterns of climate change over Morocco.

Overall, although weighting is important in summarizing the climate models’ information and reducing the projected changes’ uncertainties, it represents some limitations. In particular, we illustrated that metric-based weighting does not always lead to considerable improvements compared to the basic ensemble average. Using model weighting approaches may require more understanding of the physical processes related to the application of interest.