1 Introduction

El Niño-Southern Oscillation (ENSO) is the most prominent short-term climate oscillation on Earth, which significantly influences the climate and weather anomalies in most regions globally. Therefore, it is significantly important to study and predict ENSO, which has been the focus of atmospheric and marine sciences since the 1980s (Cane et al. 1986; Zebiak and Cane 1987; Ji et al. 1996; Latif et al. 1998; Behringer et al. 1998; Kang and Kug 2000; Barnston et al. 2012; Ham et al. 2012; Chen et al. 2004, 2015; Tang et al. 2018; Peng et al. 2018; Ham et al. 2019). Although scientists have made significant progress in theorizing ENSO as well as in observing and predicting it over the years, many problems continue to exist. For example, currently, more than 20 models exist to issue real-time forecasts from 6 months to 1 year (https://iri.columbia.edu/climate/ENSO/currentinfo/update.html). However, these models have produced different results, suggesting a significant uncertainty in ENSO predictions (Chen and Cane 2008; Jin et al. 2008; Tippept et al. 2012; Luo et al. 2018). In particular, the occurrence of two strong westerly wind bursts (WWBs) in early 2014 apparently prompted some models to predict an extreme event, which failed to materialize in fact, due to the absence of additional WWBs activity (Menkes et al. 2014; Hu and Fedorov 2016). Not only that, the boreal summer easterly wind burst had the effect of preventing and then reversing the discharge of the equatorial heat content which helped push the 2015–2016 El Niño event to extreme magnitude (Levine and McPhaden 2016). The intra-seasonal wind bursts in the tropical Pacific challenged almost all ENSO prediction models, stimulating a new round of research on ENSO globally (Lian et al. 2017).

The Lamont-Doherty Earth Observation (LDEO) model, developed by Cane and Zebiak in the mid-1980s, is the earliest physically based ENSO forecast model (Cane et al. 1986; Zebiak and Cane 1987). Chen et al. (1995) adopted a more balanced scheme to improve the quality of the initial fields, which made a significant improvement to its prediction ability. Later, its initialization schemes were further developed by incorporating sea level and wind data (Chen et al. 1998, 1999). Subsequently, its prediction skill became comparable to the most advanced coupled general circulation models (CGCMs) after a bias-correction method was incorporated that reduced large systematic model biases (Chen et al. 2000). This model has since become a benchmark for ENSO prediction models and has been intensively used in simulating and predicting ENSO in the past decades (Cheng et al. 2010; Wu 2016; Peng et al. 2018; Zhao et al. 2019). Since its latest version LDEO5 was reported in the seminal paper by Chen et al. (2004), this model-based prediction system has not been further developed.

This study provides an extension to the LDEO5 prediction system. It includes two critical improvements over LDEO5. First is regarding its initialization scheme. LEDO5 has been using a nudging scheme to assimilate sea surface temperature (SST) anomalies and other satellite derived products for initialization during the operational services. The rapid development of data assimilation methods in recent years, especially the Ensemble Kalman Filter (EnKF) and other ensemble-based methods, have greatly advanced the initialization study (Zhang et al. 2005; Deng et al. 2009, 2010; Zheng et al. 2006; Wu 2016). Compared to the nudging scheme, the EnKF scheme considers observation errors, thus, alleviating the imbalance in model dynamics and physics to some extent. Thus, in this study, we construct a weak coupling assimilation system based on EnKF to assimilate SST and wind stress anomalies for producing balanced initial conditions. The second issue addresses the uncertainties caused by stochastic noises (Kleeman and Moore 1997; Moor and Kleeman 1999; Zheng et al. 2009a; Cheng et al. 2010). To account for these uncertainties in prediction systems, an effective strategy is to perform ensemble predictions (EPs) and the uncertainties are valued using probabilistic measures (Chen and Cane 2008; Zheng et al. 2009b; Cheng et al. 2010; Wilks and Vannitsem 2018). For a noise-free model, such as LEDO5, stochastic optimals (SOs) analysis are considered efficient to generate ensemble predictions (Farrell and Ioannou 1993; Kleeman and Moore 1997). Thus, we employ SOs to represent the effect of atmospheric stochastic processes on ENSO prediction errors. In addition, we also conduct a long-term ensemble hindcast for the past 163 years using the new system. This study is built upon and expands the study conducted by Chen et al. (2004) from a single prediction to multiple-member ensemble predictions.

This paper is structured as follows. In Sect. 2, the model and method are described, including a brief introduction of the LDEO model, EnKF algorithm, and SOs construction. In Sect. 3, the ensemble coupled data assimilation (CDA) system is introduced and assimilation experiments carried out are described. In Sect. 4, the EP system is elaborated, and retrospective forecasts are carried out. Summary and discussion are given in Sect. 5.

2 Model and methodology

2.1 The LDEO model

The LDEO model is an ocean–atmosphere coupled model and its components are briefly described as follows. The atmospheric dynamics are loosely governed by steady state and linear shallow-water equations (Gill 1980), which are forced by the heating anomalies parameterized by SST anomalies and moisture convergence. The integral range of the atmospheric model spans over the domain of 101.25° E–286.875° E and 29° S–29° N, with the grid spacing of 5.625° (longitude) × 2° (latitude). The oceanic dynamics are simulated using a reduced-gravity model, which is forced by the wind stress anomalies from the atmospheric model. The integral range of the oceanic dynamics spans over the domain of 125° E–281° E and 28.75° S–28.75° N, with a grid spacing of 2° (longitude) × 0.5° (latitude). The oceanic thermodynamics are modeled by a three-dimensional nonlinear equation for the SST anomalies, covering the domain of 129.375° E–275.625° E and 19° S–19° N, with the same grid as that of atmospheric model. The model time step is 10 days. More details about the LDEO model can be found in Zebiak and Cane (1987).

2.2 EnKF algorithm

The EnKF has been widely used in earth sciences for many decades. In simple terms, the analysis equation of the EnKF can be expressed as follows:

$${\text{X}}_{a} = {\text{ X}}_{b} + BH^{T} \left( {HBH^{T} + R} \right)^{ - 1} \left[ {y - H\left( {X_{b} } \right)} \right]$$
(1)

where \({\text{X}}_{a}\), \({\text{X}}_{b}\), \(B\), \(R\), \(H\), \(y\), and \(T\) denote the analysis values, background values, background error covariance, observational error covariance, transform matrix, observations, and transposition in mathematics, respectively. In this study, we use the EnKF to build the assimilation system using following procedures.

First, the initial SSTA are perturbed to generate ensembles. The integrations are defined as background values, which are used to estimate background error covariance. Then, the analysis values are obtained using Eq. (1), with the given observations and their error covariance. Each ensemble member has an analysis value and the ensemble mean represents a final analysis. This procedure cycle is repeated until the observations are not available. More procedural details can be obtained from Ham et al. (2009) and Tang et al. (2016).

2.3 SOs algorithm

SOs, which represent the spatial pattern of noise most efficient in causing error growth within a dynamical system, is widely used in noise-free models (Farrell and Ioannou 1993; Kleeman and Moore 1997; Tang et al. 2005,2008; Moore et al. 2006). It has been reported that SOs can produce a good ensemble and improve the ENSO predictability (Tang et al. 2008; Liu et al. 2019).

For white noise in the time, the SOs are eigenvectors of the operator S, which is expressed as follows:

$$S = \mathop \int \nolimits_{0}^{{T^{\prime}}} R^{*} \left( {0,t} \right)R\left( {0,t} \right)dt$$
(2)

where \(T^{\prime}\) is the forecast interval of interest, \(R\left( {0,t} \right)\) is the forward tangent propagator of the linearized dynamical model that advances the state vector of the system from time 0 to \(t\) and \(R^{*}\) is the adjoint of \(R\). The latest studies have shown that, there is a close relationship between WWBs and ENSO (Karspeck et al. 2006; Gebbie et al. 2007; Lopez and Kirtman 2014). In this study, only atmospheric stochastic processes are considered and the SOs are constructed by perturbing the wind stress anomalies during the entire prediction integration. It should be noted that, the SOs may include but not limited to WWBs process. More procedural details of SOs can be obtained from Tang et al. (2005) and Moore et al. (2006).

3 Ensemble coupled data assimilation system

In this section, an ensemble CDA system is developed based on EnKF. Assimilation experiments are carried out for the past 163 years, which generate the initial conditions for ENSO prediction used in the next section.

3.1 System establishment and experiment design

Mostly, EnKF has two limitations due to a finite ensemble size. First limitation is the spurious correlation between model states and remote observations, while the other is the negative bias of prior error variance. To address these issues, many covariance localization and inflation techniques have been proposed (Gaspari and Cohn 1999; Zhang et al. 2005; Bishop and Hodyss 2009; Raeder et al. 2012; Wu 2016). In this study, localization coefficients used are in the form of Gaspri-Cohn function (GC function; Gaspari and Cohn 1999), which is the most widely used function to cut off the long-distance correlations. After a series of tests, the best result is obtained by taking four times distance between the adjacent grids as much as the decorrelation length. For covariance inflation, we use static multiplicative method. The factors, from 1.0 to 1.6, with an interval of 0.05, are gradually tested. The best factor in this work is 1.2.

The SST and zonal wind stress (ZWS) anomalies are assimilated in a framework of weak coupling assimilation. Three experiments are conducted to evaluate the performance of the assimilation system. First, a comparison test is conducted to assimilate SST anomalies using the nudging method. Second, SST anomalies are assimilated using the EnKF. Last, SST and ZWS anomalies are assimilated using the EnKF. The three experiments are named exp. 1, exp. 2, and exp. 3. The Kaplan SST anomalies from January 1856 to December 2018, for the region of 97.5° E–287.5° E, − 32.5° S to 32.5° N, with 5° resolutions on both longitude and latitude and the ECMWF twentieth century reanalysis (ERA-20C) wind data from January 1900 to February 2010 for the region of 0° E–358.875° E, 89.1415° S–89.1415° N are assimilated into LDEO5 for model initialization (called ensemble scheme). It should be noted that before assimilation, the monthly Kaplan SST anomalies and ERA-20C wind data are interpolated into the grids of LDEO5 model after space–time smoothing. Here, the initial SST anomalies perturbations are random numbers in a Gaussian distribution, with a mean of 0 and variance of 1 °C. Whereas, the observational perturbations are random numbers in a Gaussian distribution, with a mean of 0 and a variance of 0.1 °C and 0.01 dyn/cm2. In this study, the assimilation frequency is once a month with the ensemble size of 100.

3.2 System analysis

The analyses and simulations from the ensemble CDA system are examined in this study. Figure 1 shows the time series of observed and analyzed Niño3.4 SST anomalies in the three experiments. It can be seen that all the analyses are found to be in good agreement with the observed values in the three experiments. As in Chen et al. (2004), the modeled SSTA are nudged toward the observed data by a simple nudging scheme, i.e., using observed SSTA to replace model counterpart. The correlation is found to be 0.9896 in exp. 3, which is larger than that of exp. 2. In other words, the SST anomaly analyses in assimilating multi-source data are better than that in assimilating single-source data. The same conclusions are obtained when the results are evaluated using Niño 3 index. Thus we always use Nino3.4 for evaluation in following discussions unless indicated otherwise.

Fig. 1
figure 1

Time series of observed (red) and analyzed (blue) Niño3.4 SST anomalies in a exp. 1, b exp. 2, c exp. 3, respectively

Full size image

From top to bottom, Fig. 2 shows the time series of ensemble spread and root mean square (RMS) errors before and after assimilation of Niño3.4 SST anomalies in exp. 3. It can be seen that the ensemble spread has an appropriate order, same as that of variance of observational error. The time-averaged RMS error is found to be 0.1505 after assimilation and it significantly decreases compared to that of before assimilation, which is found to be 0.4749.

Fig. 2
figure 2

Time series of a ensemble spread and b RMS errors before and after assimilation of Niño3.4 SST anomalies in exp. 3

Full size image

In addition to the SST anomalies, assimilated data also include the ZWS anomalies, which are available from January 1900 to February 2010. Figure 3 shows the time series of observations and analyses, as well as the ensemble spread and RMS errors before and after assimilation of ZWS anomalies in the Niño3.4 region. It can be seen that the analyses are in agreement with the observed values, with the correlation of 0.9376. Further, the ensemble spread has an appropriate order, same as that of variance of observational error. The RMS error is observed to be 0.0744 after assimilation, which decreases to a certain extent compared to that of before assimilation, which is observed to be 0.1008.

Fig. 3
figure 3

Time series of a ZWS anomalies in the Niño3.4 region (red, observed; blue, analyzed), b ensemble spread and c RMS errors before and after assimilation of ZWS anomalies in the Niño3.4 region in exp. 3

Full size image

The above-mentioned results indicate that this ensemble CDA system successfully assimilated multi-source data. It also suggests that the system should be investigated for its ability to simulate other variables. Figure 4 shows the time-longitude diagram of the upper layer depth (ULD) anomalies in the equatorial region from Simple Ocean Data Assimilation (SODA) reanalysis and simulation. It can be seen that the ensemble CDA system captures the characteristics of the thermocline variability, amplitude, and eastward propagation.

Fig. 4
figure 4

Time-longitude diagram of the ULD anomalies in the equatorial region from a SODA reanalysis and b simulation

Full size image

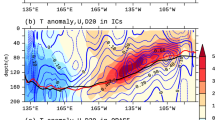
The subsurface thermal variability is an important factor that dominates ENSO variation. Figure 5 shows the evolution of the subsurface temperature (Te) anomalies averaged over the Niño3.4 region, from SODA reanalysis and simulations. The correlation between SODA reanalysis and simulations is found to be 0.7953.

Fig. 5
figure 5

Evolution of the Te anomalies averaged over the Niño3.4 region from SODA reanalysis and simulations

Full size image

The above-mentioned results indicate that the ensemble CDA system simulated the ULD and Te anomalies well. The other two experiments exhibit similar performance, which are not presented in detail in this paper. Additionally, the three assimilation experiments generate three groups of initial conditions for ENSO prediction for the past 163 years.

4 Ensemble prediction system

In this section, an EP system with SOs representing the atmospheric stochastic processes is developed. Using the initial conditions mentioned in Sect. 3, three ENSO prediction experiments are carried out for the past 163 years, namely exp. 4, exp. 5, and exp. 6. To further demonstrate the advantage of assimilating multi-source data, a single forecast with the averaged initial conditions of exp. 6 is also carried out, namely exp. 7. The settings of the four forecast experiments are summarized in by Table 1.

Table 1 Settings of the four forecast experiments
Full size table

4.1 System development and experiment design

The ensemble CDA system provided initial ensembles for exp. 5 and exp. 6; thus, we only consider atmospheric stochastic processes in the two experiments and constructed the SOs by perturbing the wind anomalies during the entire prediction integration. For comparison, exp. 4 is a single hindcast initialized by the nudging scheme, while exp. 7 is a single hindcast initialized by the averaged initial conditions of exp. 6. Figure 6 depicts the leading EOF mode of all the first SOs, representing the fastest error growth of SST anomalies due to stochastic processes that are incorporated into wind anomalies. It shows large amplitudes in the eastern equatorial Pacific, indicating that the uncertainties of winds in this area mostly influence on the prediction error of SSTA in this model. This is quite consistent with the recent work of Hu and Fedorov (2018) that highlighted the important role of cross-equatorial winds in the tropical Pacific climate mean state and variability. Four hindcast experiments are carried out covering the period of 1856–2018, each lasting for 12 months and initialize from the beginning of each calendar month.

Fig. 6
figure 6

Leading EOF mode of the first stochastic optimal wind stress anomalies for the past 163 years

Full size image

4.2 System analysis

The anomaly correlation coefficients (ACCs) and RMS errors of the predicted ensemble mean of Niño3.4 index relative to the observations are used to evaluate the overall predictability of ENSO. Figure 7a and b show the ACCs and RMS errors between the observed and forecasted Niño3.4 SST anomalies, as a function of leading months. It can be seen that the forecast skill in exp. 4 is the worst, whereas exp. 6 gives the best skill. Furthermore, the forecast skills in exp. 5 and exp. 7 lie between the both, indicating that assimilating multi-source data yields better results and SOs plays a beneficial impact on the forecast skill. The error bars shown in Fig. 7a and b suggest that, for most leading months, the skill difference between Exp. 5 and Exp. 6 exceeds their sampling errors.

Fig. 7
figure 7

a ACCs and b RMS errors between the observed and forecasted Niño3.4 SST anomalies in leading months in the four forecast experiments

Full size image

Figure 8 shows the variations of ACCs with respect to lead time and start time for exp. 6. It is shown that the prediction skill is somewhat dependent on the season. Specifically, the prediction shows high skill in boreal summer and low skill in spring. The latter is generally referred to as the well-known spring predictability barrier (SPB) phenomenon (Webster and Yang 1992; McPhaden 2003; Duan and Wei 2013). However, the SPB here is not as severe as that in persistence or in most other forecast models, implying that the SPB in this prediction system is reduced to some extent. The same results can be found from exp. 4, exp. 5 and exp. 7 (not shown).

Fig. 8
figure 8

ACCs of the predicted Niño3.4 SST anomalies as a function of start month and lead month

Full size image

Figure 9 shows the time series of the observed and forecasted Niño3.4 SST anomalies from exp. 6 at leading 3, 6, 9, and 12 months for the past 163 years. It can be seen that the forecasts fit the observations sufficiently well, except for some predictions at leading 9 and 12 months. The correlation skill is 0.75 at lead time up to 6-month, which is comparable with the current best level and better than that of original LDEO5 (Barnston et al. 2012; Li et al. 2015; Ren et al. 2017; Chen et al. 2004). Moreover, most large El Niño and La Niña events occurred during the past 163 years are forecasted successfully at leading 12 months by the EP system.

Fig. 9
figure 9

Time series of observed (red) and forecasted (blue) Niño3.4 SST anomalies: a 3 months lead time, b 6 months lead time, c 9 months lead time, d 12 months lead time, respectively

Full size image

Probabilistic skill measures the ability of the system to predict the probability distribution of the occurrence of events. Talagrand diagrams are considered to be effective for such evaluation (Talagrand et al. 1998; Hamill 2001; Zheng et al. 2009b). Talagrand diagrams are generated by sorting each ensemble from the smallest to the largest for each grid point. With 100 members, this creates 101 intervals. The observation then falls into one of the 101 bins, which forms a diagram of the frequencies as a function of the bin index. Figure 10 shows the Talagrand diagrams for Niño3.4 SST anomalies for the past 163 years. It can be seen that the probability distribution is relatively flatter, except the two extreme bins on both sides. It is observed to be closer to the expected averaged probability, indicating that the ensembles show a good identity. For different lead times, it is found that the shorter the lead time, the better the distribution. In conclusion, the probability distribution of the observations can be well represented using the ensemble approach.

Fig. 10
figure 10

Talagrand diagrams for the SST anomalies in the Niño3.4 region: a 3 month lead time, b 6 month lead time, c 9 month lead time, d 12 month lead time. Dashed line indicates the expected value

Full size image

The relative operating characteristic (ROC, Mason and Graham 1999) is chosen to measure the ensemble forecast performance probabilistically. It compares the fraction of events properly forewarned against the fraction of nonevents occurring after a warning is issued. ROC curves for the Niño3.4 SST anomalies at the lead times of 3, 6, 9, and 12 months are shown in Fig. 11. For all the lead times, all the points on ROC curves of three different event types are found to cluster in the upper-left corner of the diagram, indicating that the system consists of relatively large hit rates and small false alarm rates. This implies that the system exhibits forecast skill for all the three event types. For all the lead times, warm events are found to be well predicted, followed by cold events. It possesses relatively lower skill for the neutral events.

Fig. 11
figure 11

ROC curves for a 3 months lead time, b 6 months lead time, c 9 months lead time, d 12 months lead time

Full size image

5 Discussion and conclusions

The LDEO model has played a central role in understanding and predicting ENSO. Its latest version LEDO5, developed in the late 1990s, continues to be intensively used in ENSO studies. In this study, we improved its initialization system and extended it from a single prediction to ensemble run.

An ensemble CDA system was first developed based on the EnKF, and afterwards, assimilation experiments were carried out for the period of 1856–2018. The results showed that higher assimilation skills were obtained by assimilating multi-sources data. Further, it was found that the RMS errors significantly decreased after assimilation, compared to before assimilation. In addition, the system performed well in simulating the ULD anomalies in the equatorial region and the Te anomalies in the Niño3.4 region.

Afterwards, an EP system was developed by adding the SOs onto the wind stress anomalies. Retrospective forecasts were carried out for the past 163 years with the EP system. The comparison revealed that the forecast skills, obtained from assimilating multi-sources data, were higher than any other, which was comparable with the world advanced level. The SPB was not very severe with our EP system. In terms of probabilistic forecast, the probability distribution of observations was well represented by the ensembles. All three types of events showed probabilistic prediction skills, with the best exhibited for warm events, followed by cold and neutral events.

This work has provided the foundation for the application of EnKF and atmospheric perturbations for ENSO prediction. Although better predictions were made by assimilating multi-source data, the assimilation system was in the framework of weak coupling, which did not sufficiently utilize observed information. The strong coupling assimilation can further enhance the physical correlation and consistency of the model parameters in the coupled system. However, it has two limitations due to the mismatch between the time scales of different components, namely the significant challenge to accurately estimate the coupling error covariance, and the large noises introduced by the accumulation of sampling error. Many strategies have been formulated to address the above-mentioned limitations (Aksoy et al. 2006; Zheng and Zhu 2010; Wu et al. 2012; Zhang et al. 2012, 2015; Han et al. 2013; Liu et al. 2014; Lu et al. 2015). Therefore, it is important to further study the practical application of the strong coupled data assimilation in an operational ENSO prediction system, like LEDO5, which we will carry out in the future. In the present work, ensemble members were constructed by perturbing initial conditions and SOs were adopted to represent the atmospheric stochastic forcing. There are many other approaches to deal with initial perturbations and model errors, such as conditional nonlinear optimal perturbations (CNOPs) and nonlinear forcing singular vector (NFSV) based ensemble forecasts (Duan and Zhou, 2013; Duan et al. 2016; Duan and Huo 2016; Huo et al. 2019; Tao and Duan 2019). It is interesting to apply for these methods for further exploring ENSO predictability, which is under our way.