1 Introduction

The El Niño–Southern Oscillation (ENSO) is the largest source of interannual variability in the Tropics, and manifests as anomalous sea surface temperatures in the Eastern and Central Pacific Ocean. El Niño (EN), the phase with anomalously warm sea surface temperatures in this region, has been shown to impact surface climate around the globe. While in a qualitative sense the Northern Hemisphere response to EN in boreal winter and spring over North America has been known for several decades (Bjerknes 1969; Horel and Wallace 1981; Mo and Livezey 1986; Ropelewski and Halpert 1987; Sardeshmukh and Hoskins 1988; Halpert and Ropelewski 1992; Trenberth et al. 1998) and includes warm wintertime temperatures over Northwestern North America and excess precipitation over the southern United States, there are several open questions.

No two EN events have identical sea surface temperature (SST) anomalies, and hence the teleconnections from each event may differ due to differences in either the location of peak convective anomalies or in the strength of the underlying event. While stronger EN events should be expected to induce a stronger tropical/subtropical Rossby wave source (e.g. Frauen et al. 2014), identical sea surface temperature anomalies located in different regions will not, in general, lead to the same tropical rainfall response due to the existence of a minimum threshold for deep convection (Chiodi and Harrison 2013; Frauen et al. 2014; Johnson and Kosaka 2016). This asymmetric tropical rainfall response, could in principle drive nonlinearities in the extratropical troposphere (Hoerling and Kumar 1997; Hoerling et al. 1997, 2001).

Whether nonlinearity—i.e. a response not proportionate with the underlying tropical SST forcing—is in fact present in the extratropical response is not clear. While the observational composites of Hoerling and Kumar (1997) clearly show evidence for nonlinearity between EN and La Niña (LN), the observational composites of DeWeaver and Nigam (2002) which sample a different period, and those of Deser et al. (2017) and Deser et al. (2018) which sample the period 1920 to 2013, exhibit weaker nonlinearity. This difference could be due to decadal variability, though it is not clear whether this decadal variability is forced (Gershunov and Barnett 1998; Zhou et al. 2014) or reflects internal atmospheric variability. Relatedly, Deser et al. (2017) and Deser et al. (2018) argue that many of the purported “nonlinearities” in ENSO teleconnections may in fact be an artifact of internal variability, and that there have not been enough events in the observational record to fully establish the details of the North Pacific response forced by ENSO. Namely, if one subsamples observed sea level pressure patterns from all ENSO events since 1920, the North Pacific response to a given ENSO phase can differ by a factor of two depending on which specific events are included in the subsample. This difference is not due to differences in the strength of the underlying ENSO events sampled, and is rather likely due to internal variability. Hence, apparent nonlinearities in the response to EN vs. LN and between moderate vs. strong events may in fact be an artifact of the still-short observational record (\(\sim \) 20 EN and 14 LN events are considered in the studies of Yu et al. 2012; Deser et al. 2017). Kumar and Chen (2017) also highlight the role of internal atmospheric variability for the apparent failure of seasonal forecasts for United States West Coast precipitation during the very strong EN of 2015/2016. The difficulty in isolating nonlinearity in the presence of large internal variability is consistent with early work using idealized models: the extratropical response to ENSO is driven in large part by a positive feedback from extratropical transients (Held et al. 1989) and extraction of energy from zonal asymmetries in the extratropical basic state (Simmons et al. 1983; Branstator 1985), and both of these features involve internal extratropical dynamics and are inherently noisy.

Even if one considers equally strong EN events, there is an additional source of inter-event variability: the degree to which strong sea surface temperature anomalies extend into the Central Pacific. Specifically, several papers have argued that the atmospheric response to EN events that peak in the central equatorial Pacific (CP EN events), also called dateline or Modoki EN events (Larkin and Harrison 2005; Ashok et al. 2007), differs from that in response to EN events that peak in the eastern equatorial Pacific (EP EN events; see the recent review by Capotondi et al. 2015). While all EN types lead to a deepened Aleutian low (Weng et al. 2009; Yu and Kim 2011), it has been suggested that central Pacific (CP) EN leads to a westward and southward displacement of the deepened Aleutian low and different impacts on United States precipitation and temperature (Larkin and Harrison 2005; Weng et al. 2009).

However, the extratropical response to CP is not robust across the various CP definitions that have been proposed: for example, the precipitation anomalies over the United States in response to CP EN differ between the studies of Weng et al. (2009) and Larkin and Harrison (2005), the temperature anomalies over the United States in response to CP EN differ between the studies of Larkin and Harrison (2005) and Johnson and Kosaka (2016) (see also Yu et al. 2015), and the upper tropospheric height patterns in Garfinkel et al. (2013) for a range of CP definitions are qualitatively different. It is unclear whether these differences actually reflect a forced response to the slightly different sea surface temperature patterns during the events composited, or are due to unforced variability that happened to be present in the years composited (Garfinkel et al. 2013; Deser et al. 2017). Furthermore, many ENSO events cannot be cleanly labeled either EP or CP (Johnson 2013; Capotondi et al. 2015), and thus for any CP/EP definition there will be ambiguities as to how to classify marginal events (and the specific years deemed marginal in turn depends on the CP/EP definition adopted, Garfinkel et al. 2013). Finally, CP EN events tend to be weaker than EP EN events (Capotondi et al. 2015), and it is conceivable that the relatively weak teleconnective response to CP EN (Yu et al. 2015) may be due to the relative strength of the underlying events as opposed to differences in the spatial distribution of sea surface temperature anomalies.

Despite all these difficulties in isolating nonlinearities in the observed extratropical response to ENSO, nearly all modeling experiments with a large enough sample size have succeeded in identifying nonlinearities (e.g. Hoerling et al. 1997, 2001; Hoerling and Kumar 2002; Garfinkel et al. 2013; Frauen et al. 2014; Johnson and Kosaka 2016), though with the caveat that the nonlinearities tend to be weak in comparison with internal variability and are only identifiable upon averaging over many events (Hoerling and Kumar 2002; Garfinkel et al. 2013). This motivates the following two questions: (a) In what regions will nonlinearities first begin to become identifiable above the noise as sample sizes increase? (b) How large of a model ensemble is necessary before these nonlinearities manifest themselves?

We answer these questions by first identifying the nonlinear responses to ENSO in an ensemble of 42 integrations using the Goddard Earth Observing System Chemistry-Climate Model (GEOSCCM; Rienecker et al. 2008; Oman and Douglass 2014) in the North Pacific and North American sectors. We then consider how many events must be averaged together before these nonlinearities emerge from noise. In all cases, we consider the following three forms of nonlinearity or differences among ENSO flavors: (1) antisymmetry between EN and LN; (2) a disproportionately stronger response for a stronger event; and (3) differences in impact between CP and EP events.

After introducing the data and methods in Sects. 2 and 3, we demonstrate that nonlinearities in the central North Pacific response to ENSO, where the SLP response to ENSO peaks, are only robust upon averaging over several dozens of events (Sect. 4.1). In contrast, nonlinearities are more salient to the north and east of this region (Sect. 4.2), and also over select populated regions of North America (Sect. 5), after averaging only 10–20 events. These nonlinearities in the SLP response account for nonlinearities in the surface temperature and precipitation response over North America. All of these nonlinearities can be traced back to the wavenumber spectrum of the tropical precipitation anomalies. After discussing the implications for the observed response to ENSO (Sect. 6), we summarize our results.

2 Data

The foundation of this study is an ensemble of simulations conducted using the GEOSCCM. This model couples the GEOS-5 (Rienecker et al. 2008; Molod et al. 2012) atmospheric general circulation model to the comprehensive stratospheric chemistry module StratChem (Pawson et al. 2008). The model has 72 vertical layers, with a model top at 0.01 hPa, and all simulations discussed here were performed at 2\(^\circ \) latitude × 2.5\(^\circ \) longitude horizontal resolution. The model spontaneously generates a QBO (Molod et al. 2012). An enhanced stratospheric resolution has been shown to be crucial for a correct stratospheric and Eurasian response to ENSO (Bell et al. 2009; Cagnazzo and Manzini 2009; Hurwitz et al. 2014), and we consider nonlinearities in these regions in a follow-on paper. Fine stratospheric resolution is likely less important for the North Pacific and North American response (e.g. Bell et al. 2009). 42 ensemble members covering the period 1980 to 2009 are analyzed, and all impose observed SST variations globally. Full details of the model ensemble are included in Garfinkel et al. (2017).

By forcing the model with historical SSTs, we allow for a more natural comparison to the observed response to ENSO as compared to simulations with annually repeating identical SST anomalies [as analyzed by Garfinkel et al. (2013)] or idealized SST patterns (Frauen et al. 2014; Hegyi et al. 2014). However we acknowledge that the imposing of SSTs violates energetic constraints and does not allow for the generation of self-consistent SST anomalies and teleconnections. Hence it is worth revisiting all conclusions we make in this paper in a different model configuration.

Model output is compared to meteorological fields from MERRA (Modern-era retrospective analysis for research and applications; Rienecker et al. 2011) reanalysis, precipitation from the GPCP v2.3 (updated from Adler et al. 2003), and surface air temperature from Berkeley Earth (updated from Rohde et al. 2013).

3 Methods

ENSO events are identified based on the November through February (NDJF) seasonal mean SST anomalies in the ERSSTv5 dataset (Huang et al. 2017) with a 1981–2010 base period. EN events are identified when SST anomalies in the Niño3.4 region (5S–5N, 170W–120W), are larger than 0.5 K, and LN events are identified when SST anomalies in this region are more negative than − 0.5 K. EN and LN events are further categorized into four groups similar to Hurwitz et al. (2014): Eastern Pacific (EP) EN, characterized by positive SST anomalies in the Niño-3 region (5S–5N, 210E–270E), and Central Pacific (CP) EN, characterized by positive SST anomalies in the Niño-4 region (5S–5N, 160E–210E), as well as EP and CP LN events, characterized by negative SST anomalies in the same two regions. EP EN events are identified when the Niño-3 anomaly is 0.1 K larger than the corresponding Niño-4 anomaly. Similarly, EP LN events are identified when the Niño3 anomaly is 0.1 K less than the Niño-4 anomaly. CP EN and CP LN events are identified analogously. All remaining years, either because they are neutral ENSO or because the Niño-3 and Niño-4 anomalies are within 0.1K of one another, are categorized as “other events”. We emphasize that the “other events” composite includes events that are difficult to classify unambiguously as EP or CP due to relatively similar anomalies in the Niño-3 and Niño-4 regions despite having strong anomalies in the Niño-3.4 region (e.g. 2002/2003 and 2006/2007). The years included in each composite are listed in Table 1. As the response to CP LN and EP LN are not robustly different in these integrations despite the availability of hundreds of model-seasons (as shown below in select figures), we combine these two composites, as well as LN years that cannot be unambiguously classified as either EP or CP, into a single LN composite for most of our figures. Composited anomalies during EP and CP events depend on the specific definition adopted, however the two years identified herein as CP EN (1994/1995 and 2004/2005) are so classified for nearly all CP definitions (e.g Garfinkel et al. 2013; Johnson and Kosaka 2016), and much of the uncertainty discussed by Garfinkel et al. (2013) arises from the decision on how to classify marginal events which in our study fall into the “other events” composite.

Table 1 Events composited for GEOSCCM and observations
Full size table

When considering the linearity of ENSO teleconnections, we stratify years by their SST anomalies in the Niño3.4 region during NDJF for simplicity. However, we acknowledge that the choice of which single index is most closely associated with the extratropical response likely depends on the specific extratropical region examined (L’ Heureux et al. 2015; Yu et al. 2015). The supplement considers sensitivity to stratifying EP events by the Niño-3 anomaly and CP events by the Niño-4 anomaly.

As we would like to discern whether differences in the response to EP EN and CP EN are due to differences in the position of tropical convection and not due to differences in event amplitude, we further divide the EP EN composite into “extreme” events (i.e. 82/83 and 97/98) and “moderate” events (i.e. 1986/1987, 1991/1992). Note that SST anomalies in the Niño3.4 region are still \(\sim 30\%\) stronger for the moderate EP EN events than for the CP EN events.

Most ENSO events peak in the late fall or early winter, and decay by the following spring. However the peak response in California precipitation occurs only in late winter and early spring (Jong et al. 2016). In addition, the peak lower-stratospheric response in observations (Manzini et al. 2006; Garcia-Herrera et al. 2006), in previous modeling studies (e.g. Cagnazzo et al. 2009), and in the model experiments described in this paper only occurs in late winter (not shown), and hence we consider the response separately from December through February and in early spring (March and April).

Anomalies are computed as follows. A monthly climatology over the full duration of each model experiment, reanalysis product, and observational dataset is computed, and is then subtracted from the raw fields to generate monthly anomalies. All anomalies are then detrended by removing the linear trend over the period 1980 through 2009.

Statistical significance for the anomalies in a composite relative to climatology and for the difference between two composites is computed using a two-tailed Student-t test at the \(95\%\) confidence level. For figures showing maps of anomalies, stippling indicates grid boxes that are not significant based on a false discovery rate of 10% following Wilks (2016). Statistical significance of the difference in slope between regression lines computed for two different ENSO types is computed by considering the interaction term when both types are included in the same regression analysis (pp. 220–228 of McDonald 2014).

4 ENSO effect in the North Pacific

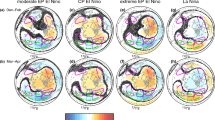
We begin with composites of sea level pressure (SLP) and precipitation using all 42 available simulations for 4 different categories: moderate EP EN, CP EN, extreme EP EN (97/98 and 82/83), and LN (Figs. 1, 2). All three EN composites show the canonical wavetrain pattern in the Western Hemisphere, with a low in the Northeastern Pacific, a high over Canada, and a low near the Eastern United States (Fig. 1), and all show enhanced precipitation in the Tropical Pacific (Fig. 2). SLP and tropical precipitation anomalies in the LN composite are to zeroth order opposite to those in the EN composites. However the location of the nodes and extrema of the wavetrain pattern in SLP differ among all four composites, and we turn our attention to these deviations. We first discuss changes in the North Central Pacific where the response to ENSO maximizes (red box on Fig. 1), and then discuss the response further north and further east ( blue and green boxes on Fig. 1).

Fig. 1
figure 1

Sea level pressure response to ENSO in GEOSCCM. The contour interval is 1 hPa. A red box demarcates the region shown in the left column of Fig. 4, a green box demarcates the region shown in the middle column of Figs. 4 and 5a, while the blue box demarcates the region shown in the right column of Figs. 4 and 5b. a, b EP El Niño events excluding those in 1982/1983 and 1997/1998; c, d CP El Niño events; e, f 1982/1983 and 1997/1998; g, h La Niña. (Top) December through February and (bottom) March and April. The zero line is thick black. Statistical significance is computed using a two-tailed Student’s t test using all 42 integrations with a 95% confidence threshold, and stippling indicates grid boxes that are not significant based on the use of a false discovery rate of 10% following Wilks (2016)

Full size image
Fig. 2
figure 2

Precipitation anomalies (mm/day) in the GEOSCCM integrations in December-February. The contour interval is 0.4mm/day. Red and blue boxes demarcate regions shown in Figs. 5 and 8. The zero line is thick black. Statistical significance is computed using a two-tailed Student’s t test using all 42 integrations with a 95% confidence threshold, and stippling indicates grid boxes that are not significant based on the use of a false discovery rate of 10% following (Wilks 2016)

Full size image
Fig. 3
figure 3

95% confidence intervals on the response to El Niño in the North Pacific when the full ensemble is subsampled. a Longitude of the peak response of sea level pressure from 40N–56N; b Magnitude of the peak response in the North Pacific. For b the response to La Niña is multiplied by − 1

Full size image
Fig. 4
figure 4

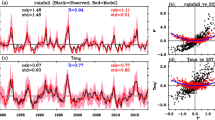
North Pacific sea level pressure response to ENSO in boreal winter and spring. a, b Sea level pressure from 40N to 56N and 180E to 220E (red box on Fig. 1); c, d 40N to 56N and 220E to 240E (green box on Fig. 1); e, f 52N to 72N and 190E to 240E (blue box on Fig. 1). (Top) December, January, and February; (bottom) March and April. Winters categorized as Central Pacific ENSO are in black, and Eastern Pacific ENSO are in blue. A linear least-squares best fit is shown in each panel, and the slope is indicated. If the slope for EP and CP events are statistically significantly different, then we show the slope for each composite separately in blue (for EP) and black (for CP). The ensemble mean response is indicated with a large x, and each integration with a dot. The response in MERRA reanalysis is shown with a diamond. Each integration has been linearly detrended before the anomalies associated with each event are computed (see Sect. 3). Note that there are winters with nearly identical mean NDJF anomalies (e.g. the La Nina events in 1999/2000 and 2007/2008), which leads to near overlap in this figure for such winters

Full size image
Fig. 5
figure 5

As in Fig. 3 but for a SLP in the Northeast Pacific (40N to 56N and 220E to 240E; green box on Fig. 1); b SLP in Alaska (52N to 72N and 190E to 240E; blue box on Fig. 1); c precipitation in the land areas within the red box on Fig. 2; d precipitation within the blue box on Fig. 2; e 2 m temperature in the land areas within the red box on Fig. 9; f 2 m temperature within the blue box on Fig. 9. For all panels, we scale the magnitude of the response to extreme EN by the magnitude of the underlying Niño3.4 anomalies as compared to the moderate EP EN composite mean (which are 55% stronger during 82/83 and 97/98 than for the two moderate EP EN events)

Full size image
Fig. 6
figure 6

Power spectrum of a precipitation from 5S to 5N and b sea level pressure from 40N-56N for the five ENSO composites. Each power spectrum is normalized so that the total power in each composite is identical. The correlation between the power spectrum for equatorial precipitation and extratropical SLP for each composite is indicated. The correlation of the power spectrum of precipitation from 5S to 5N for each of the three EN composites with sea level pressure from 40N–56N for each of the three EN composites in included in supplemental table 1. Uncertainty estimates on the power spectrum are computed using a bootstrapping with resampling technique as described in the text, and are offset slightly from the wavenumber to which they correspond for clarity

Full size image
Fig. 7
figure 7

Difference in precipitation between the moderate-EP EN and CP EN composites in boreal a winter and b spring. The left column shows the magnitude of the differences (contour interval is 0.4 mm/day). Statistical significance is computed using a two-tailed Student’s t test using all 42 integrations with a 95% confidence threshold, and stippling indicates grid boxes that are not significant based on the use of a false discovery rate of 10% following (Wilks 2016). The right column indicates the minimum number of events required in a subsample before anomalies become significant at the 95% level, with white indicating that differences are not statistically significant even with 80 events, green indicating wettening, and gray/black indicating drying. Red and blue boxes demarcate regions shown in Fig. 8

Full size image

4.1 SLP in the North Central Pacific

We first focus on the longitude of the extrema in the North-central Pacific (red box on Fig. 1). The extrema in tropical rainfall anomalies are shifted into the Central Pacific during CP events as compared to EP events (Fig. 2), and hence one might expect that the peak North Pacific response is farther to the west for CP EN as compared to EP EN. We now test this hypothesis. For each integration and each ENSO composite we compute the longitude of the extrema (minimum for EN and maximum for LN) in sea level pressure anomalies in the North Pacific averaged between 40N and 56N. While the longitude of the peak response for LN and CP EN are indistinguishable, the extrema during both CP EN and LN is approximately \(15^\circ \) further westward as compared to EP EN when averaged across the entire ensemble (\(\sim 185\)E versus \(\sim 200\)E). However, the peak longitude in any given member of the ensemble can differ by more than \(50^\circ \) from the ensemble mean location for a given composite due to internal atmospheric variability, and this internal variability is larger than the difference in the forced response between EP EN and CP EN. Only upon averaging many samples can the internal variability be averaged out to uncover differences in the forced response. We quantify the emergence of the forced signal, and specifically the number of individual winters needed before this forced response becomes robust, as follows. We bootstrap with replacement the longitude of the peak North Pacific response for a subsample of the full 42-member ensemble, with the size of the subsample increasing from 5 randomly selected events up to 75 randomly selected events for each ENSO category. We create 2000 such bootstrapped subsamples for each subsample-size. We then compute the mean and the top and bottom 2.5% quantiles without making any assumption on the nature of the distribution, and hence form 95% confidence intervals of the response. This allows us to quantify how the uncertainty in the location of the North Pacific response decreases as the number of events averaged together increases (Fig. 3a), and when \(95\%\) confidence intervals do not overlap then we consider the response to be statistically significant (note that if one assumes a normal distribution, some overlap can occur yet the difference of the means is still statistically significant). Approximately 25 individual events are necessary before the difference in peak longitude between moderate EP EN (the red line) and CP EN (black line) in Fig. 3a becomes statistically significant. A similar but weaker nonlinearity is also present between extreme EN and moderate EP EN events (compare red and magenta lines in Fig. 3a), as approximately 55 events are necessary. The implications of this result for the observed response to ENSO are discussed in Sect. 6.

We now consider the linearity of the amplitude of the extrema in SLP in the North Pacific. Figure 1 suggests that the magnitude of the peak midlatitude SLP response is weaker in the CP EN composite as compared to EP EN, and we quantify in Fig. 3b how many events are needed in order for the relative weakness of the North Pacific response during CP EN to become robust. For this panel we calculate the peak response separately for each ensemble member and ENSO composite in order to isolate where the response peaks. At least 75 events, or essentially the entire ensemble, need to be averaged together before the difference between CP EN and EP EN is statistically significant.

Can the weakness of the CP EN North Pacific response be linked quantitatively to the relative weakness in the underlying tropical forcing? To answer this, we present in Fig. 4a, b the SLP response in the central North Pacific averaged over the region indicated with a red box in Fig. 1 for each event for all 42 model integrations. Each season is stratified by its Niño3.4 anomaly, and the range of responses across all 42 ensemble members (each ensemble member is a dot), the response in the MERRA reanalysis (a diamond), and the ensemble mean (a large x), is shown. We then compute the linear best-fit regression line for all data points, and if the difference in slope between the regression line for CP and EP events is statistically significant, we list the slope separately for each. Supplemental Figure 1 is comparable but SSTs in the Nino3 region are used to characterize the strength of EP events and SSTs in the Nino4 region are used to characterize the strength of CP events. In both winter and spring, the slope of the best-fit regression line is actually steeper for CP events than for EP events (Fig. 4a, b). In other words, a given change in SSTs in the tropical Pacific leads to a stronger response for CP events than for EP events. Hence, the weakness of the CP EN North Pacific response is linked to the relative weakness in underlying tropical forcing, and not to peculiarities in the location of the SST forcing.

Next, we consider linearity between EN and LN events: is the central North Pacific response to an EN event equal and opposite to that of a LN event of comparable strength? Nonlinearity can be deduced by considering whether there are systematic differences between the ensemble mean response from the best-fit line for EN or LN events in Fig. 4a, b. As there is no indication of any such systematic differences in either Fig. 4a or Fig. 4b, there is no evidence for nonlinearity in the Central North Pacific, in agreement with Frauen et al. (2014, see their Figure 11). Finally, the blue lines on Fig. 3, which correspond to LN, fully overlap the CP EN response (shown with black lines), and hence confirm that there is no nonlinearity between EN and LN.

In conclusion, the differences in the region of strongest response in the North Pacific are only weakly nonlinear: the only nonlinearity that is salient with fewer than 55 individual events are differences in the location of peak SLP response (if more than \(\sim \) 25 events of each type are considered, the westward displacement of the CP EN response and the eastward displacement of the extreme EP response becomes robust). There are no indications of any deviations from antisymmetry between LN and (CP) EN in our GEOSCCM ensemble.

4.2 SLP in the Northeastern Pacific and Alaska

We now demonstrate that nonlinearities in the SLP response to ENSO are more salient outside of the region of strongest response. A notable feature in the SLP composites in Fig. 1 is the downstream response over North America: the CP EN wavetrain has a higher zonal wavenumber, and has nodal lines oriented more meridionally and less zonally, as compared to the EP wavetrain. For example, the nodal line between the North Pacific low and the Canadian ridge (i.e. where the response changes sign) is over the far-eastern North Pacific during CP EN but east of the Rockies during EP EN. The nodal line between the Canadian high and the Eastern United States low is located further to the west, and extends further south, during CP EN. These differences in the remote response to EN far exceed the differences in longitude and magnitude of the North Pacific response discussed in Sect. 4.1, and have implications for surface climate over North America as discussed in Sect. 5. These differences in SLP over the far-Northeastern Pacific and over Canada are consistent with those found by Johnson and Kosaka (2016), and also with the association of EP EN but not CP EN with the tropical Northern Hemisphere pattern (Yu et al. 2015). The salience of the difference in SLP in the far-Northeastern Pacific (the region indicated with a green box in Fig. 1) between the EP EN and CP EN composites is considered in Fig. 5a, where we bootstrap with replacement 2000 times a subsample of the full 42-member ensemble (as in Fig. 3). The responses to EP EN and CP EN are robustly distinguishable with 15 events averaged over in each composite. Hence nonlinearities in the Northeast Pacific are more prominent than in the central North Pacific. Supplemental figure 3 presents a map view of where SLP anomalies differ robustly between CP and EP, and confirms that differences are more robust over the far Northeastern Pacific than further west.

This shift in the downstream response is likely caused by the tropical precipitation anomalies during each EN type. Figure 6 shows the power associated with each zonal wavenumber for equatorial precipitation and for SLP averaged over 40N to 56N. Uncertainty in the power spectrum is computed by bootstrapping with replacement 42 randomly chosen ensemble members with some members necessarily repeated and others left out, calculating the power spectrum, and then repeating 2000 times. The top and bottom 2.5% quantiles relative to the mean estimate the 95% confidence intervals on the response and are indicated. Figure 6 also indicates the correlation between the power spectrum of 40N–56N SLP and the power spectrum of tropical precipitation. The power spectrum in midlatitude SLP is highly correlated with the power spectrum in tropical precipitation for all five ENSO composites, which indicates that differences in the zonal signature of the extratropical response are linked to the zonal signature in the tropics. This correspondence between the wavenumber of the tropical forcing and the extratropical response is consistent with kinematic wave theory (Hoskins and Karoly 1981). The tropical precipitation response to CP EN is weighted towards higher wavenumbers as compared to EP EN (Fig. 6a), and this tendency is mirrored in the extratropical response (Fig. 6b). Consistent with this, the correlation of the spectrum of midlatitude SLP with tropical precipitation for CP EN exceeds the cross correlation between CP EN and EP EN (supplemental table 1). Hence, the more pronounced zonal structure in the CP EN extratropical response (cf. Fig. 1) is linked to its tropical precipitation pattern, in which precipitation is confined to the tropical Central Pacific and does not extend into the East Pacific (Fig. 2).

Fig. 8
figure 8

As in Fig. 4 but for a, b precipitation over land areas area-weighted from 32N to 44N and 235E to 245E. The diamonds represent anomalies in GPCP v2.3 precipitation. c, d 2 m temperatures over land areas in North America area-weighted between 46N and 70N and 195E to 250E. e, f 2 m temperatures over the Midwest of the United States and adjoining areas in Canada (area-weighted between 40N and 52N and 255E to 280E). The diamonds represent anomalies in Berkeley Earth surface temperature in c–f

Full size image

A second robust difference in the SLP response to CP and EP lies over Alaska (the region indicated with a blue box in Fig. 1). For example, the latitude of the subpolar nodal line in the Pacific sector (i.e. the latitude the extratropical wavetrain reaches) is further poleward for EP EN (\(\sim 75\)N in Fig. 1a) as compared to CP EN (\(\sim 65\)N in Fig. 1c, consistent with Garfinkel et al. 2013), and this difference is consistent with the theory of Rossby ray propagation and stationary wavenumber developed by Hoskins and Karoly (1981) as a wave with a lower wavenumber launched towards the pole will reach a higher latitude as compared to a wave with a higher wavenumber. This difference in SLP over the region indicated with a blue box in Fig. 1 is statistically significant with only 15 events in each composite (Fig. 5b, see also Supplemental figure 3).

We now consider the question of linearity between EN and LN events—is the response to LN over Alaska and the far Northeastern Pacific symmetric to that in EN? Figure 4c, d demonstrates that the response in the far Northeastern Pacific (the region indicated with a green box in Fig. 1) is linear, as there are no systematic deviations of the ensemble mean responses from the best fit line. Namely, the blue and black points lie along the blue and black lines respectively for both positive and negative values of the Nino3.4 index. A similar picture emerges for SLP over Alaska (Fig. 4e, f). Results are similar if we use SSTs in the Nino3 region to characterize the strength of EP events and SSTs in the Nino4 region to characterize the strength of CP events (supplemental figure 2). This linearity is confirmed by Fig. 5a, b, where the LN response lies in between the EP EN and CP EN response, with CP EN serving as the closer analog to LN than EP EN.

5 ENSO impacts in North America

We now consider the downstream effects of ENSO in North America.

5.1 Precipitation

We start with the precipitation response over the Western United States, where EN usually leads to a wetter winter (Yu et al. 2015; Jong et al. 2016; Kumar and Chen 2017). Such a response is evident in the moderate EP EN composite and even more pronounced in the extreme EP EN composite (see the red box on Fig. 2), and is also evident in the difference between the moderate EP EN and CP EN composites (Fig. 7). However this difference in response between the moderate EP EN and CP EN composites is only statistically significant upon considering nearly the entire ensemble available (Fig. 5c).

Precipitation anomalies also differ significantly in the South-central United States (see the blue box in Fig. 2) between EP EN and CP EN (Fig. 7), and this difference is also evident in the composited response to observed events (Johnson and Kosaka 2016 their figure 8). This difference becomes statistically significant after more than \(\sim \)65 events of each type are selected (Fig. 5d). Changes in the precipitation response in this region are consistent with the wavetrain associated with each ENSO phase noted in Sect. 4.2: the high SLP that is confined to Canada under EP EN extends further south and west under CP EN (Fig. 1). Associated with this is a ridge aloft (not shown), and hence the eastward extension of the subtropical jet typically present during EN is less evident during CP. This leads to reduced precipitation during CP EN as compared to EP EN (cf. Johnson and Kosaka 2016, and references therein). Overall, differences between moderate EP EN and CP EN over the United States are generally small and require a large model ensemble to robustly identify.

Are there nonlinearities in the response to extreme EP EN events versus moderate EP EN events in North America? To answer this, we present in Fig. 8a, b the precipitation response over the Western United States (land areas only in the red boxed region on Fig. 2) for each event for all 42 model integrations. This figure is constructed analogously to Fig. 4: each season is stratified by its Niño3.4 anomaly, and the range of responses across all 42 ensemble members, the response in the MERRA reanalysis, and the ensemble mean, is shown. As in Fig. 4, we then compute the linear best-fit regression line for all data points, and if the difference in slope between the regression line for CP and EP events is statistically significant, we list the slope separately for each. Supplemental Figure 2 is constructed similarly but SSTs in the Nino3 region are used to characterize the strength of EP events and SSTs in the Nino4 region are used to characterize the strength of CP events. The ensemble mean response to the two strongest EP EN events in 82/83 and 97/98 (the two rightmost “x”s in the panels) lies above the best-fit line and hence shows evidence of a nonlinear response. Only 15 events are necessary before the difference between moderate EP EN events and extreme EP EN events becomes statistically significant even after we weight the response in the extreme EP EN events by its underlying Niño3.4 SST anomalies (Fig. 5c). The precipitation response over the Western United States shown here is consistent with the observed response documented by Jong et al. (2016), who show that only the strongest EN events have a pronounced impact on California precipitation, while LN and weak EN events have relatively little impact. Supplemental figure 4 presents a map view of where precipition anomalies differ robustly between extreme EP EN and moderate EP EN, and confirms that differences are robust over the Western United States.

The likely cause of this nonlinearity is the eastward extension of the North Pacific low during extreme EP events: the North Pacific low is located \(10^\circ \) further east during extreme EP EN events as compared to moderate EP EN events (Figs. 1, 3a, and Supplemental figure 5), and this eastward shift in SLP is likely forced by a similar eastward shift in tropical precipitation and tropical sea surface temperatures. The net effect is that precipitation increases over the far-Eastern Pacific and in the Western United States during extreme EP EN events. Implications for the recent 2015–2016 strong EN event are discussed in Sect. 7. Finally, there is no evidence for deviations from symmetry in the response to LN as compared to EN in Fig. 8a, b or supplemental figure 2ab.

5.2 Near-surface temperature

We next consider changes in 2-m temperature in North America in response to ENSO. Figure 9 shows composites of 2-m temperature if all model integrations are included for 4 different categories: (a) moderate EP EN, (b) CP EN, (c) extreme EP EN (82/83 and 97/98), and (d) LN. Figure 10 shows the difference in 2-m temperature between the moderate EP EN and CP EN composites. All three EN composites show warming in Northwest North America that is particularly pronounced during observed EP events (Yu et al. 2015), while cooling prevails during LN. However there are nonlinearities in the response to each ENSO phase, and we now turn attention to these nonlinearities.

Fig. 9
figure 9

As in Fig. 2 but for 2 m temperature. The contour interval is 0.5 K

Full size image

Over Northwest North America where the response to ENSO maximizes (land areas in the red boxed region on Fig. 9), there is little difference between the response to moderate EP EN and CP EN events in winter, aside from a slightly stronger warming during moderate EP EN (Fig. 10a). However this difference in the magnitude of the warming between moderate EP EN and CP EN is not statistically significant unless all simulations performed are considered (Fig. 5e). In fact, if one accounts for the strength of the events underlying the moderate EP EN and CP EN composites, CP events have a slightly stronger impact on this region than EP events (see the slopes of the best-fit lines in Fig. 8c and supplemental figure 2ab). Deser et al. (2018) also find no significant difference in the surface temperature response to CP EN as compared to EP EN over Northwest North America. The response to LN is also statistically indistinguishable from the inverse of the response to EN even if all ensemble members are considered (Fig. 5e). However, the response to extreme EP EN is not proportionately stronger. While this region does warm in response to extreme EP EN, the warming is weaker than in the moderate EP EN composite (Fig. 9a, c), and the relative cooling during extreme EP EN is statistically significant with only 20 events upon weighting the extreme EP EN response by the magnitude of its underlying Niño3.4-region SST anomalies (Fig. 5e). The temperature response in this region for each event is shown in 8c, d, and the ensemble mean response to the two strongest EP EN events in 82/83 and 97/98 (the two rightmost events in the panels) lies below the best-fit line. The likely cause of this nonlinearity is the eastward extension of the North Pacific low during extreme EP events discussed above in the context of precipitation nonlinearities: the North Pacific low is located \(10^\circ \) further east during extreme EP EN events as compared to moderate EP EN events (Figs. 1, 3a, and Supplemental figure 5). Hence the southerly winds that advect warm maritime air over Northwest North America during EN events are weaker during the strongest EP EN events, and the peak warming during extreme EP EN is instead simulated to occur over Central Canada east of the Rockies (near 100W in Fig. 9c). Supplemental figure 6 presents a map view of where temperature anomalies differ robustly between extreme EP EN and moderate EP EN, and confirms that temperatures over Western North America are warmer during moderate EP EN events than during extreme EP EN events.

Fig. 10
figure 10

As in Fig. 7 but for 2 m temperature. The contour interval is 0.5 K

Full size image

Nonlinearity is also pronounced in the warming response over the Midwestern United States and adjacent areas in Canada (indicated by a blue box in Figs. 9 and 10). Over this well-populated region, EP EN leads to warming but CP EN events do not (Fig. 9, 10). This difference is consistent with that found by Johnson and Kosaka (2016 their figure 8) and Deser et al. (2018 their figure 14) and is statistically significant with more than 20 events (Fig. 5f). Figure 8e shows the response across all integrations in the region indicated by a blue box in Figs. 9 and 10, and the slope of the best fit line for CP is significantly different to that of EP. Changes in the temperature response in this region are due to the difference in the wavetrain noted in Sect. 4.2: the high SLP that is confined to Canada under EP EN extends further south under CP EN (Fig. 1). Associated with this High are northerly winds that advect cold subpolar air southward over Southern Canada and the Midwestern United States.

6 Realism of model variance

As noted by Deser et al. (2017), a necessary prerequisite for comparing observed and modeled ENSO teleconnections is for the model to simulate a similar amount of variance as compared to that observed, as otherwise the model does not satisfactorily capture internal atmospheric variability. We now discuss whether GEOSCCM simulates a realistic amount of variance in the regions discussed earlier. We evaluate the variance by computing the variance of the monthly anomalies in each region for each of the 42 ensemble members, sort the variance for the 42 members, and evaluate where the observed/reanalysis variance would lie if we were to consider it as “ensemble member 43”. The range of model variance is indicated with a vertical line on Fig. 11, and the observed variance is indicated with a diamond. The realism of model variance has also been assessed by following the procedure used in figure 1 of McKinnon et al. (2017), and results are presented in Supplemental Figures 7–9. All conclusions drawn below as to regions with biased model variance are consistent with the conclusions that can be drawn from Supplemental Figures 7–9.

For both SLP in the Central North Pacific and over Alaska (the red and blue boxed regions in Fig. 1), the variance in reanalysis data lies well within the variance simulated by GEOSCCM, and hence we expect that our conclusions with regards to uncertainties in the effect of ENSO in this region are relevant to nature as well.

In contrast, all 42 GEOSCCM integrations simulate less variance over the Northeast Pacific region (the region indicated with a green box in Fig. 1) than is found in observations (Supplemental Figure 7), though the difference between the variance in the integration with the most variance and in reanalysis data in winter is only \(2\%\) (Fig. 11) and this bias disappears in March and April (19 of 42 model integrations simulate less variance than has been observed). This effect is evident in Fig. 4c: the observed response in the two most extreme EN events and in the most extreme LN event are larger than in any GEOSCCM integration (the observed response is shown in diamonds in Fig. 4). Recall that in this region GEOSCCM simulated a qualitatively different response to CP vs EP, with only EP leading to lower SLP in this region, and that only 15 events are necessary in order to reach this conclusion (Fig. 5a). There are (at least) two implications for this bias in variance in this region in applying our findings from GEOSCCM to nature: first, the error bars indicated on Fig. 5a are likely too small; and second, the slopes of the best fit regression line in Fig. 4c are also likely too small (indeed the best fit slope for observed EP ENSO events in this region is \(-2.0\pm 1.3\) hPa/K as compared to \(-1.3\pm 0.1\) hPa/K for GEOSCCM). The first of these effects would imply that our conclusions based on GEOSCCM might overestimate the robustness of the nonlinearity, while the second implies that our conclusions based on GEOSCCM underestimate the degree of nonlinearity. It is unclear how to quantify the net of these two effects, and hence the degree to which ENSO’s response in this region is nonlinear can only be fully quantified upon considering additional models. That being said, a similar nonlinearity is evident in both the observational and model composites of Johnson and Kosaka (2016) (see their figure 6) including in models with far fewer ensemble members than those which are available here, and hence this nonlinearity appears robust.

Fig. 11
figure 11

Comparison of the variance in each member of the GEOSCCM ensemble (vertical line) to the variance in observations/reanalysis data (diamond) for seven key regions discussed in the text in winter (December through February)

Full size image

Most GEOSCCM ensemble members simulate less variance in precipitation over the Western United States than has been observed (Fig. 11), but a few integrations do simulate quantitatively similar variance, and hence there is no conclusive evidence of a model bias. In contrast, GEOSCCM does suffer from too little variance in precipitation over the Central United States (blue boxed region in Fig. 2; Fig. 11). Note that the observational composites of Johnson and Kosaka (2016) show a statistically significant difference between EP and CP in this region even though far fewer events are included in their composites than we expect should be required. This suggests that GEOSCCM may be underestimating the degree of nonlinearity in this region. Ultimately, conclusions regarding the degree to which variability in this region is nonlinear need to be confirmed with other models.

Finally, GEOSCCM simulates realistic variability in near-surface temperatures over the Midwest United States, though too much variability over Northwest North America (Fig. 11; Supplemental Figure 9). Recall that nonlinearities in near-surface temperatures over Northwest North America were most pronounced during extreme EP EN events: the extreme EP EN events in our model ensemble led to less warming than might be expected given the strength of the underlying event. The diamonds in Fig. 8c, d, which show the response in reanalysis data, suggest that this nonlinearity is present in nature for the 97/98 and 82/83 events as well as the observed warming during both events in this region was weak. However, future work with other models should explore whether the biased variability in GEOSCCM in this region may lead to a faulty estimate of the degree of nonlinearity.

Overall, GEOSCCM simulates realistic variance in most of the regions considered by this paper and therefore satisfactorily simulates internal atmospheric variability. Even for regions where GEOSCCM suffers from biases in the variance, the observed nonlinearity in the response to ENSO appears similar to that simulated by GEOSCCM.

7 Conclusions

Pronounced nonlinearities are evident in the response to ENSO. The most prominent nonlinearities are listed in Table 2, and are summarized here. In the Central North Pacific region where the SLP response to ENSO peaks (the region indicated with a red box in Fig. 1), nonlinearities are relatively muted (Figs. 3, 4a, b). There is no indication of any nonlinearities between EN and LN. The response to strong EN events peaks slightly to the east of that for moderate EN events, though this effect is only evident upon averaging more than 55 events. Nonlinearities between CP and EP events in the longitude (amplitude) of the peak response are statistically significant only upon averaging 25 (75) events.

Table 2 Summary of nonlinearities
Full size table

In contrast, changes in SLP to the east of this region (far-Northeastern Pacific) and to the north of this region (over Alaska) in response to different ENSO phases are more clearly nonlinear. The anomalous low over the central Pacific extends beyond the far-Northeastern Pacific into North America during EP EN, but does not during CP EN. This difference in the downstream response is statistically significant upon considering more than 15 events in GEOSCCM (Figs. 4c, d, 5a), and is consistent with the response in observations and in other models as well (Johnson and Kosaka 2016). This nonlinearity can be related back to the zonal wavenumber of the tropical precipitation response: the precipitation response to EP EN is weighted towards lower wavenumbers than that of CP EN, and the wavenumber composition of the precipitation dictates the wavenumber composition of the extratropical response (Fig. 6). There is no evidence for nonlinearities between EN and LN or between extreme EN and moderate EN events in this region (Fig. 4c, d). However GEOSCCM simulates slightly too-weak internal atmospheric variability in this region (Fig. 11), and our conclusions as to the degree of nonlinearity in this region should be considered preliminary.

Robust nonlinearity is also evident over Alaska: the anomalous low over the central Pacific extends northward into Alaska during EP EN, but does not during CP EN (Figs. 5b, 4e, f). This difference in the downstream response is statistically significant with 15 events in GEOSCCM. This difference can also be related back to the zonal wavenumber spectrum of the tropical precipitation (Fig. 6). In contrast, there is no evidence for nonlinearities between EN and LN or between extreme EN and moderate EN events in this region (Fig. 4e, f).

Nonlinearities in precipitation over the Western United States (see the red box on Fig. 2) between EP EN and CP EN, or between LN and EN, are statistically significant only upon considering nearly the entire ensemble available (Figs. 5c, 8a, b). In contrast, extreme EP EN events lead to disproportionately increased precipitation in this region, and this increase is detectable with more than 15 events. This nonlinearity can be related back to the eastward extension of the North Pacific low (Figs. 1, 3a).

Precipitation anomalies also differ significantly in the South-central United States (see the blue box on Fig. 2) between EP EN and CP EN if more than 65 events of each type are selected (Fig. 5d). However our model suffers from biased variance in this region (Fig. 11), and the observed difference in precipitation in this region is statistically significant despite far fewer observed events (Johnson and Kosaka 2016).

Over Northwest North America where the surface warming response to EN maximizes (land areas in the red boxed region on Fig. 9), there is no significant difference between the response to moderate EP EN and CP EN events or between EN and LN unless all available integrations are considered (Figs. 5e, 8c, d). However, the response to extreme EP EN is not proportionately stronger, and only 15 events are needed to detect such a nonlinearity. This nonlinearity can be related back to the eastward extension of the North Pacific low for extreme EP EN events discussed above, as the peak warming is further east over Central Canada (Fig. 9).

The Midwestern United States and adjacent areas in Canada cool during CP EN events but not during EP EN events (Figs. 5f, 8e, f), and this difference is statistically significant with more than 20 events. This nonlinearity is also due to the difference in the zonal wavenumber of the wavetrain (Fig. 6).

In all regions at least 10 events of each type are necessary before nonlinearities can be identified as statistically significant at the \(95\%\) confidence level, and the nonlinearities that emerge fastest from the noise are between different classes of EN events rather than between EN and LN. Given that only approximately 20 EN events and 14 LN events are considered in the observational studies of Yu et al. (2012); Deser et al. (2017, 2018), it is not surprising that it has been difficult to establish conclusively the nature of nonlinearities using observational data. Similarly, it is not surprising that different studies that evaluate different eras or select different sets of events should reach different conclusions as to the degree of nonlinearity (Hoerling and Kumar 1997; Hoerling et al. 1997, 2001; DeWeaver and Nigam 2002; Yu et al. 2015; Deser et al. 2017), as randomly chosen subsamples of the response differ qualitatively in all regions examined (Figs. 3, 5). Indeed, the simplest explanation for the differences in the extratropical teleconnnections across these studies is that internal variability still clouds our ability to discern nonlinearities using the observational record between EN and LN, between moderate EN and extreme EN, and between CP and EP, in agreement with Deser et al. (2017, 2018).

Our simulations do not include the recent strong EN event in 2015/2016, and hence we cannot quantify the cause(s) of the failure of seasonal forecasts for Western United States precipitation in that season (Kumar and Chen 2017). However, it is evident from Fig. 8a, b that a few individual ensemble members simulate a drier Western United States during the 97/98 and 82/83 events, even though the ensemble mean and most individual integrations clearly indicate a wetter winter as indeed occurred. Hence variability in precipitation in this region has both a forced and unforced component (Zhang et al. 2018; Lim et al. 2018; Jong et al. 2018), and it is premature to conclude anything about the forced response to the SST anomalies present in 2015/2016 from the observed lack of increased precipitation in California. As discussed above, the increase in precipitation over the Western United States during extreme EN events is only expected to become statistically significant if more than 10 extreme EN events are compared to the composited response for moderate EP EN events. That being said, other studies have provided evidence that the dryness in Southern California during the 2015/2016 event specifically arose partially from SST variability in the Pacific Ocean (Siler et al. 2017; Jong et al. 2018; Lim et al. 2018).

The results presented in this work are based on atmospheric GCM experiments with imposed observed SST anomalies. It is conceivable that the extratropical response in the ensemble mean is due not only to the large-scale tropical Pacific SST anomalies, but also to the small-scale structure of tropical SST anomalies (or SST anomalies in other basins). It is also reasonable to ask whether the extratropical response in our composites is the result of a single outlier included in a given composite, and is not truly representative of the other members in that composite. Figs. 4 and 8 indicate these potential complications are not a major concern: these figure consider each ENSO event separately, and for all 6 metrics shown on these figures and for both boreal winter and spring, the ensemble-mean response to events with closely-spaced Nino3.4 indices is similar. Furthermore, we have computed the ensemble-mean longitude of the North Pacific low for the two years in each of the three EN composites separately (e.g. Fig. 3), and the mean location for the two CP EN years is similar (\(186.5^\circ \)E and \(185.1^\circ \)E), the mean location for the two EP EN years is similar (\(201.4^\circ \)E and \(204.5^\circ \)E), and likewise the mean location for the two extreme-EP EN years is similar (\(208.9^\circ \)E and \(213.5^\circ \)E). Hence there is no indication that our results are aliased by the peculiarities of the SST anomalies in a specific event rather than representing the response to the large-scale tropical SST anomalies.

The results presented in this work are based on a single GCM, and hence must be confirmed with other models and modeling configurations. However model biases in variance were not present over most of the key regions we identified, and even for regions with biases we find similar results to previous studies using other models or observations. Hence we would be surprised if additional models with realistic variance disagreed strongly with our results.

ENSO affects variability in the NH polar stratosphere and over Eurasia as well (Manzini et al. 2006; Garfinkel and Hartmann 2007; Ineson and Scaife 2009; Bell et al. 2009; Cagnazzo and Manzini 2009), and we are currently preparing a follow-up to this paper that addresses the degree to which the response to ENSO is nonlinear in these regions.