Assessment of natural climate variability using a weather generator

Abstract

It is common practice to use a 30-year period to derive climatological values, as recommended by the World Meteorological Organization. However this convention relies on important assumptions, of which the validity can be examined by deriving the uncertainty inherent to using a limited time-period for deriving climatological values. In this study a new method, aiming at deriving this uncertainty, has been developed with an application to precipitation for a station in Europe (Westdorpe) and one in Africa (Gulu). The weather generator framework is used to produce synthetic daily precipitation time-series that can also be regarded as alternative climate realizations. The framework consists of an improved Markov model, which shows good performance in reproducing the 5-day precipitation variability. The sub-seasonal, seasonal and the inter-annual signals are introduced in the weather generator framework by including covariates. These covariates are derived from an empirical mode decomposition analysis with an improved stability and significance assessment. Introducing covariates was found to substantially improve the monthly precipitation variability for Gulu. From the weather generator, 1,000 synthetic time-series were produced. The divergence between these time-series demonstrates an uncertainty, inherent to using a 30-year period for mean precipitation, of 11 % for Westdorpe and 15 % for Gulu. The uncertainty for precipitation 10-year return levels was found to be 37 % for both sites.

1 Introduction

Using a 30-year period to define climatology is a common practice. Adopted by the World Meteorological Organization (WMO) for defining normals, the use of such a period has become a key to perform model evaluations, climate sensitivity studies as well as almost any climate analysis. Guttman (1989) describes the two main historical steps that led to the current definition of climate normals and the use of 30-year periods; In the beginning of the 20th century, the climate was described as stationary over periods longer than human experience (Landsberg 1972). Using a long observational period was therefore advised to improve the quality of the estimation of time-series statistics. However, at this time, observations were usually covering short and differing periods. In 1935, the WMO decided to use a 30-year period, namely 1901–1930, to define as normals, what seems to be a compromise between the period duration covered by observations and the quality of normals’ estimations.

After the concept of stationarity climate became obsolete (Landsberg 1972), the WMO proposed to use sliding 30-year periods to define these normals. Currently, WMO normals are updated every decade. The reason to use a 30-year period instead of a longer period is not a problem of observations’ availability anymore, but a need to relate normals to the current climate. Currently, this is still the definition of climate normals.

This latter definition encompasses two assumptions that can be described using the concept introduced by Hasselmann (1976), which consists in representing the climate with a rapidly varying “stochastic” component and a slowly varying “deterministic” component. The first assumption is that 30 years is assumed to be enough to average the stochastic component out. The second assumption is related to using the past 30 years to derive the current normals. It implicitly assumes the stationarity of the slowly varying component on the last 30 years.

Because the WMO definition of a 30-year period to define climatology is well established, analyses related to climate are generally performed using such a period. Using another time-period, especially shorter, is often criticized and regarded as non-representative of the climatology, although it shares similar assumptions as the 30-year period. Therefore the question remains on how large the inherent uncertainties are for describing the climatology on a basis of a limited period?

Livezey et al. (2007) proposed an alternative method to derive climate normals that is not based on a fix period duration and that accounts partially for the non-stationarity of the “slowly responding” component over the last 30 years. Although this work is a step forward towards a better description of climatology values, uncertainties related to the period under investigation still need to be assessed.

Global circulation models (GCMs) can also provide estimates of the uncertainty inherent to WMO assumptions by using ensemble methods. The advantage of using GCMs is the use of equations that aim at reproducing the deterministic climate signal and stochastic processes. In addition it is possible to get an estimation of the uncertainty inherent to WMO assumptions over large areas. Altough GCMs provide good estimations of large-scale climatology, the resolution of these models remain currently too coarse to give accurate information at the regional scale (Wilby and Wigley 1997). To correctly estimate the uncertainty, a further downscaling is needed (e.g. using RCM). Therefore the use of these dynamical models to correctly derive this uncertainty is a rather costly and complex solution. It is still performed on small integration periods in internationally coordinated projects such as the CORDEX project (http://wcrp.ipsl.jussieu.fr/cordex/about.html).

This study proposes a method to analyse the uncertainty inherent to using a limited time-period for deriving the climatology. It uses the framework of weather generators to provide synthetic time-series or possible climate realizations, that include slow (deterministic) and rapid (stochastic) variations (Hasselmann 1976). The rapidly varying component is associated with processes occurring on a daily scale (front occurrence, convection, etc), while the slowly varying component is more related to climate-scale processes (the solar cycle, ENSO, NAO, trends, etc). The weather generator reproduces the rapidly varying component via the use of the Markov model framework. The slowly varying component is extracted using an adaptation of the empirical mode decomposition (EMD) developed by Huang et al. (1998) and is used as covariates in the weather generator. Then the divergence of the synthetic climate realizations derived from the weather generator are used to quantify the climatology uncertainty for both the averaged precipitation and precipitation return levels.

A few studies have already proposed methods to derive this uncertainty (Leith 1973; Pavia 2004) but to our knowledge it is the first time that uncertainty includes not only the rapidly varying component, but also the slowly varying component. Considering the slowly varying component may be crucial for deriving accurately this uncertainty. Another innovative aspect of this study is the generation of alternative climate realizations on the daily time-scale. Such time-series can, therefore, be used to derive uncertainty not only related to averages, but also to more complex statistics such as the return levels.

The observations and the method used to produce alternative climate realizations are described in Sect. 2. An evaluation of this method is performed on a European and an African station in Sect. 3 together with the presentation of derived climatological uncertainty. Sections 4 and 5 close the paper with discussions and conclusions.

2 Dataset and methods

2.1 Dataset

The precipitation datasets are derived from tipping bucket systems and were downloaded from the Global Historical Climatology Network-Daily (GHCN-D) data (Menne et al. 2012). In total, two different stations, namely Westdorpe (${51^\circ } 13^{\prime }$N, ${3^\circ } 52^{\prime }$E) and Gulu (${2^\circ } 45^{\prime }$N, ${32^\circ } 20^{\prime }$E), respectively located in Western Europe and Africa were considered. The motivation for having different locations lies in the different characteristics of the slowly varying signal. While Westdorpe is characterized by a weak precipitation seasonal cycle and a little sensitivity to long term natural oscillations, Gulu experiences long dry and wet periods and has known some strong inter-annual variation in the previous decades (Nyeko-Ogiramoi et al. 2013; Taye and Willems 2011, 2012; Willems 2013). Daily data are used, allowing estimations of extreme precipitation events. All precipitation values lower than 0.3 mm are set to zero to account for the presence of dewdrops that can distort the result (Tu et al. 2005). A 95-year dataset was available for Westdorpe while only 59 years were available at Gulu. In addition for Gulu some data gaps (1.5 % of the dataset) were filled using the weather generator described in Sect. 2.3.

2.2 General methodology

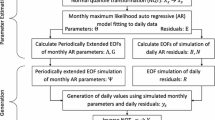
A description of the general methodology, developed in this paper, is shown in Fig. 1. A 4-step procedure, indicated with arrows in Fig. 1, is applied to each time-series. The first step is to produce 1,000 precipitation time-series using a model referred to as WGEN-WOC (Weather generator without covariates). This weather generator models precipitation occurrence through the use of a Markov model and precipitation intensity using gamma and generalized Pareto (GP) distributions. The time-series produced by the WGEN-WOC represent the stochastic component retrieved from the observation. The second step is to retrieve the deterministic signal, that consists of pseudo-cycles and a trend, from the observation. This step is performed by applying the empirical mode decomposition (EMD), to both the observations and the time-series derived in the first step. In a third step, both precipitation occurrence and intensity are modelled using the deterministic signal as covariates in a model referred to as WGEN-WC (Weather generator with covariates). Another 1,000 time-series which include both the stochastic and deterministic components, are derived from this step. Finally, in the fourth step, these time-series are post-processed to estimate the uncertainty induced by using a fixed time-period in classical statistical analyses related to climatology.

Fig. 1

Flowchart describing the general methodology proposed in this paper. The four different methodological steps are indicated with numbers. Grey shades were added to indicate our contributions to the existing scientific literature. To ease the reading, acronyms are used in the flowchart: HnMM2—homogeneous nth order Markov model with 2 states; NH2MM3—non-homogeneous 2nd order Markov model with 3 states; NHnMM3—non-homogeneous nnd order Markov model with 3 states; GP generalized pareto, EMD empirical mode decomposition

2.3 Step 1: modelling the rapidly varying component (WGEN-WOC)

2.3.1 Modelling precipitation occurrence

The precipitation occurrence is modelled using the framework of Markov models, a concept first applied to precipitation by Gabriel and Neumann (1962). Since then it has been extensively used to model precipitation stochastically for different locations. The concept behind the Markov model is that the prediction of a non-continuous variable—each unique value defining a state—at the time-step t is dependent on previous time steps. Transition probabilities define this dependency by defining the chance that a transition from state to state occurs. The following three parameters characterize these transition probabilities, namely the order, the number of states and the homogeneity.

• The order of the model defines the number of previous time-steps considered in the model

• The number of states defines the number of unique values that the non-continuous variable can take.

• The (non-)homogeneity indicates if transition probabilities are time-(in)dependent.

In this study two Markov models with different parameters are combined to represent precipitation occurrence. The first model is a homogeneous nth order Markov model with two states (HnMM2) with n varying from 1 to 10 depending on the location. The two states refer to dry and wet days. For each location the best order is derived based on the lowest Akaike Information Criterion (AIC—Akaike 1974). The transition probabilities are calibrated by the maximum likelihood method which, for the Markov model, consists of setting them equal to the ratio of observed transitions.

The second model is a non-homogeneous 2nd order Markov model with 3 states (NH2MM3). Using three states allows to discriminate intense precipitation from non-intense precipitation, a discrimination justified by the fact that these two types of precipitation often result from different physical processes (e.g. convective vs non-convective precipitation). The threshold above which precipitation is considered to be intense is set to the 95 % quantiles of each station throughout this paper. The threshold 95 % was selected based on the good performance of the different models when this value was used. For more simplicity, this threshold is referred to as TR95. Therefore a day with precipitation accumulation equal to 0 mm is assigned the state 1, a day with precipitation accumulation higher than 0 and lower than TR95 is assigned the state 2, while a day with precipitation accumulation higher than or equal to TR95 is assigned the state 3. The order of the model is limited to 2 due the relative low probabilities of having 3 consecutive days assigned to state 3 which might result in assigning a value of 0 to this transition probability, preventing them from ever happening. This wouldn’t be correct in a Bayesian framework such as the one used for generating data. This model is also non-homogeneous, meaning that the transition probabilities are evolving in time. This is implemented by making the transition probabilities dependent on covariates derived from the EMD methods (described in Sect. 2.4.1).

More details on the method used to combine the two models, namely the HnMM2 and the NH2MM3, can be found in "Appendix". The generation is performed randomly by using the derived probability transition values.

2.3.2 Modelling precipitation intensity

Precipitation intensity is modelled using truncated gamma and GP distributions depending on the state that characterizes the day, respectively low and medium precipitation quantiles and high precipitation quantiles. To ensure continuity of the combined distribution, the scale factor of the GP distribution is adjusted as described in Furrer and Katz (2008). The shape parameter of both models is kept unconstrained. These fits are performed using the maximum likelihood method. The generation is performed randomly.

2.4 Step 2: extracting the slowly varying signal

2.4.1 Deriving intrinsic mode functions

Many techniques can be used to provide covariates to the weather generator with the most popular being the Fourier transformation and the wavelet analysis. Unfortunately not all required assumptions, such as linearity or stationarity, are valid for climate data, especially for daily precipitation. The empirical mode decomposition (EMD), a technique developed by Huang et al. (1998) that decomposes a signal into intrinsic mode functions (IMFs), does not require the time-series to follow such assumptions. The EMD method has also the advantage of being totally empirical, leading to more objective analyses. In addition IMFs have time-dependent amplitude and frequency and are orthogonal to each other. The decomposition performed by the EMD can be described as follows:

$$\begin{aligned} x(t)=\mathop {\sum \limits _{i=1}^n} IMF_{i}(t) + R(t) \end{aligned}$$

(1)

where $x(t)$ is the time-series to be processed, $IMF_{i}$ is one of the $n$ IMFs derived from the EMD and $R(t)$ is the residual also called trend. The algorithm used to perform an EMD is based on a 3-step iteration procedure:

• 1. The local extrema of the signal $x(t)$ are identified and two spline interpolations are performed on the minima (Smin) and on the maxima (Smax) separately.

• 2. The mean of the envelope (Smean) delimited by Smin and Smax is then extracted. For practical reasons a “sifting process”, which consists in repeating the step 1 and 2 using Smean instead of $x(t)$, is applied until its mean is found to be smaller than a given threshold defined as advised by Rilling and Goncalves (2003)

• 3. The derived signal is an IMF. It is removed from $x(t)$ and the three steps are repeated with the remaining signal in order to obtain a second IMF. The process stops when only 2 extrema can be found in the remaining signal. This final remaining signal $R(t)$ can be identified as a trend.

2.4.2 Assessing the significance of intrinsic mode functions

One of the bottlenecks of the EMD is that, although this study aims at extracting physically meaningfulness signals, no information is provided concerning IMFs’ physical meaningfulness. It is, therefore, necessary to assess the physical meaningfulness of each IMF. This is a critical step as using non-physically meaningful information to derive climate realizations would restrain the variability between the different realizations. This restriction would, therefore, result in an underestimation of the natural climate variability estimation. In the following, the physical meaningfulness of an IMF is assessed by deriving the significance of an IMF. The significance of an IMF is defined by the latter having a variability or energy significantly higher than the energy of an IMF derived from noise.

Wu and Huang (2004) have shown that when applied to a normalized white noise time-series, the product of the energy density of the derived IMFs and their corresponding averaged period is equal to 1, leading to:

$$\begin{aligned} \log {\bar{E_{i}}} = \log {\bar{P_{i}}} \end{aligned}$$

(2)

where $\bar{E_{i}}$ and $\bar{P_{i}}$ are respectively the energy density and the average period of an $IMF_{i}$. $E_i$ is equal to the variance of $IMF_{i}$ and $P_i$ is derived using the following formula:

$$\begin{aligned} P=\frac{2 \cdot \varDelta t}{N-1} \end{aligned}$$

(3)

where $\varDelta t$ is the time-period separating the first and last extrema of the time-serie and N is the total number of extrema. Wu and Huang (2004) have also shown that the energy density of each IMF is normally distributed. From these conclusions they developed a method that allows the assessment of IMF significance compared to white noise based on a simple equation:

$$\begin{aligned} \log {\bar{E_{i}}} > \log {\bar{P_{i}}} + k \sqrt{\frac{2}{n}} e^{\frac{\log {\bar{P_{i}}}}{2}} \end{aligned}$$

(4)

where n is the number of samples in $x(t)$ and $k$ is a constant determined by the significance level required. As $IMF_{i}$ is normally distributed, $k$ also corresponds to the quantiles of a Gaussian distribution. For the 1, 5 and 10 % significance level, the $k$ values equal 2.326, 1.645 and 1.282 respectively. This method allows a direct estimation of the significance of IMFs by comparing their energy densities to those of IMFs derived from white noise time-series. It assumes that the analysed signal can be decomposed to

$$\begin{aligned} x(t)=WN(t)+S(t) \end{aligned}$$

(5)

where $WN(t)$ corresponds to a white noise signal and $S(t)$ a significant signal. Nevertheless, according to Hasselmann (1976), precipitation alike many other meteorological variables, can be described as:

$$\begin{aligned} x(t)=RN(t)+S(t) \end{aligned}$$

(6)

where $RN(t)$ represents the rapidly varying component which has red variance spectra and $S(t)$ corresponds to the slowly varying component which is resulting from deterministic processes. Franzke (2009) has shown that Eq. 2 changes to Eq. 7 when applied to time-serie derived from an AR(1) process.

$$\begin{aligned} \log {\bar{E_{i}}} = a\log {\bar{P_{i}}} \end{aligned}$$

(7)

where $a$ is a constant dependent to the autocorrelation degree of the time-series. Therefore Eq. 4 is also changed to Eq. 8 to account for the separate character of the meteorological data spectra.

$$\begin{aligned} \log {\bar{E_{i}}} > a\log {\bar{P_{i}}} + k \sqrt{\frac{2}{n}} e^{\frac{a\log {\bar{P_{i}}}}{2}} \end{aligned}$$

(8)

In this study, the time-series under investigation are characterized by a maximum auto-regressive order of 5 days. However, because IMFs are derived from monthly time-scales time-series, these time-series are, therefore, assumed to be approximatively equivalent to an AR(1) process. This assumption was found to be a reasonable hypothesis empirically. Equations 7 and 8 are, consequently, also valid for the time-series under investigation in this study.

The IMFs are computed for the synthetic time-series derived from the weather generator WGEN-WOC described in Sect. 2.3 (black points in Fig. 2). The value of $a$ is estimated using Eq. 7 and IMFs computed from 1,000 synthetic time-series. The fit is performed using $i$ ranging from 2 to 7. $IMF_{1}$ was excluded from this fit because $IMF_{1}$ doesn’t fulfil the hypothesis of normality assumed to derive Eq. 2. As shown in Fig. 2, the fitted line derived from Eq. 7 is well centred on all IMFs suggesting that the introduction of the parameter $a$ was sufficient to account for autocorrelation. In addition, the upper dotted line that indicates the threshold above which IMFs are significant (1 % level) is rather well located. Indeed on average about 20 points for each IMFs (black points) are located above this significance line which correspond to 2.5 % of the points.

In Wu and Huang (2004) the energy of the IMFs derived from a time-series are rescaled by adding $\log {\bar{E_{1}}}-\log {E_{1}^{obs}}$ to $\log {\bar{E_{i}}}$ for each i. Indeed in this study it is considered that the first IMF is characterized by pure noise in both the observation and the synthetic time-series. To avoid such assumption, it is proposed to substitute the $IMF_{1}$ generated from observations by a $IMF_{1}$ derived from a synthetic time-series and then only adjust all $\log {\bar{E_{i}}}$.

Fig. 2

Illustration of the method used to assess the significance of the IMFs at Gulu for the occurrence of low and medium quantiles of precipitation intensity. The black points represent IMFs derived using the synthetic time-series from WGEN-WOC. The green points are those obtained with the original observations while the red points are derived using the perturbed observed time-series (see Sect. 2.4.3 for more information). The black line results from the linear fit described by Eq. 7. The dotted line is the significance line derived from Eq. 8

2.4.3 Assessing the robustness of intrinsic mode functions

Due to the iterative nature of the EMD, the first IMFs may have an impact on all IMFs when applied to complex data. Consequently, introducing a perturbation in the original signal may disturb the decomposition and result in the production of IMFs significantly differing from IMFs derived from the original signal. This issue, known as the mode mixing problem (Huang et al. 1999; Wu et al. 2009), is critical because applying the EMD to the original signal only, may not exhaust all possible IMFs. It is, therefore, possible that an EMD would not result in extracting some physically meaningful variability in one single IMF. Instead, this physically meaningful variability would be spread in different IMFs. This spread into these IMFs (referred to as contaminated) has two main consequences; First, the spread of the variability decreases the chance to identify this signal as a significant signal. Second, the contaminated IMFs will be composed from part of the physically meaningful variability together with some random signal. If the physically meaningful variability is high, the IMF may be found to be significant but will still encompass more noise than desired. To solve these issues, a method based on the study of Wu et al. (2009) is applied. Wu et al. (2009) use a noise assisted data analysis technique which consists in building an ensemble of IMF by introducing some white noise into the original signal before performing the EMD. This method, referred to as the Ensemble EMD (EEMD), allows to exhaust all possible IMFs from the original signal. As advised by Wu et al. (2009), the amplitude of white noise introduced in the original signal is about $0.2$ standard deviation of that of the original signal. In Wu et al. (2009), all $IMF_{i}$ of the ensemble are averaged separately for each i. In this study, only the significant $IMF_{i}$ are averaged. This selection of significant IMFs is motivated by the assumption that only physically meaningful IMFs are significant while non-physically meaningful signals or random signals are non-significant (as described in Sect. 2.4.2). Restricting the averaging to significant IMFs only would, therefore, reduce the part of the random signal compared to the physically meaningful one in the resulting IMF. In addition, to avoid having two IMFs or more describing the same physical meaningful variability, the IMFs resulting from the EEMD are used as covariates only if more than half of the ensemble members are significant. Therefore instead of applying the EMD directly to the original signal (e.g. observed or synthetic time-series), it is applied to an ensembles of 1,000 time-series that are created by adding some random perturbations (red points in Fig. 2). When more than 50 % of the IMFs derived from these ensemble members are significant, their average is computed. This average is referred to as AIMF.

The spread of IMFs derived from perturbed time-series (red points in Fig. 2) is not as strong as the spread of IMFs derived from the synthetic time-series (black points in Fig. 2). This indicates that the perturbation introduced in the observation is preserving the signal present in the original data. Finally, the 6th IMF derived from the observation (green points in Fig. 2) is not considered to be significant while most of the 6th IMFs derived from the perturbed time-series are. This shows the relevance of the randomization procedure to increase the robustness.

A last step before using the AIMFs is to ensure their independence. This is performed by comparing the Pearson correlation coefficient for each possible combination of 2 significant AIMFs ($AIMF_{i}$ and $AIMF_{j}$ with $i\ne j$) to a threshold. First, a randomization procedure, consisting in randomly distributing the daily values of the original time-serie in time, is applied 1,000 times to each AIMFs (e.g. $AIMF_{i}$ and $AIMF_{j}$). This procedure results in the generation of 1,000 time-series for each AIMFs (e.g. $AIMF_{i}$ and $AIMF_{j}$). Second, Pearson coefficients are calculated between each randomized $AIMF_{i}$ and $AIMF_{j}$. Finally the threshold is defined as the 99th percentiles of the Pearson coefficients derived in the previous step. If two AIMFs are found to be mutually dependent then they are summed.

2.5 Step 3: modelling the rapidly and the slowly varying components (WGEN-WC)

The rapidly varying component is modelled using WGEN-WOC as described in Sect. 2.3. To account for the slowly varying component, independent covariates are added to each model of the WGEN-WOC. In total four different statistics are used as covariates. They are all calculated on a monthly scale as shorter period memory has already been derived from the WGEN-WOC. Two of these statistics are related to the precipitation occurrence, namely the percentage of occurrence of low and medium precipitation quantiles and the percentage of occurrence of high precipitation quantiles. Two others are related to precipitation intensity, namely the average values of low and medium precipitation quantiles and the average values of high precipitation quantiles. When, within a month, no day characterized by low and medium (high) precipitation quantiles has occurred, the lowest corresponding intensity is assigned (e.g. 0 mm for low and medium precipitation quantiles, and TR95 for high precipitation quantiles). The EMD is applied to each of these four statistics, resulting in four different datasets of AIMFs. The significant AIMFs of each statistic is used as a covariates for an element of the WGEN-WOC. The two covariates related to precipitation occurrence are calibrated to the associated transition probabilities of the Markov model NH2MM3. The covariates related to the precipitation intensity of low and medium quantiles and the high quantiles are respectively calibrated to the gamma and generalized Pareto distribution through their respective scale parameters.

3 Results

3.1 Empirical mode decomposition

For each station a different set of AIMFs was found to be significant using the criteria described in Sect. 2.4.2. A summary of these AIMFs is given in Table 1. In order to ease the interpretation, AIMFs are classified in the following 4 different categories:

• The sub-seasonal AIMFs, characterized by a period of about 6 months. They only occur at the station Gulu and are due to the displacement of the Inter-Tropical Convergence Zone (ITCZ)

• The seasonal cycle, characterized by a period of about 12 months. It occurs at all stations for all fields and is highly significant. An example of such an AIMF is shown in Fig. 3. Note: Some seasonal cycle signals were found to spread over different AIMFs. Although the EEMD is attenuating mode mixing, it remains an issue for highly significant AIMF (not shown).

• The inter-annual cycle characterized by a period longer than a year and the occurrence of at least 3 extrema. For Westdorpe only one of these AIMFs is significant, namely the AIMF that describes the occurrence of the low and medium quantiles precipitation intensity. This AIMF is having a similar frequency as the north Atlantic oscillation (NAO) as illustrated in Fig. 3. At Gulu, an AIMF with a period of about 25 years is found to be significant for the occurrence of the low and medium precipitation quantiles.

• The residual AIMFs, that can be seen as a trend, characterized by the occurrence of less than 3 extremas. These AIMFs are significant for the averaged intensity of precipitation low and medium quantiles, occurrence of precipitation low and medium quantiles in Westdorpe (shown in Fig. 3) and the occurrence of precipitation low and medium quantiles in Gulu. The first two trends are monotonic and show an increase in the occurrence of events and a decrease in their intensity. The last trend is not monotonic and it seems that the time-serie is not long enough to have these AIMFs defined as a long term pseudo-cycle.

Fig. 3

Illustration of three AIMFs derived from the occurrence of low and medium precipitation quantiles at Westdorpe. The seasonal cycle is plotted for a 10 years period only to provide more details while the inter-annual cycle and the trend are plotted for the full period of observation. The NAO and the inter-annual cycle extracted from the observations are shown as 5-year running averages

The degrees of significance of these AIMFs, that also denote the amplitude and therefore impact, are varying from station to station. In general it was found that Gulu contains AIMFs at a higher significance level than Westdorpe. This shows that the slowly varying component has higher influence on Gulu precipitation than one Westdorpe’s one.

Table 1 Summary of AIMFs extracted from both Westdorpe and Gulu

3.2 Evaluation of the weather generator

The evaluation of the weather generators (WGEN) is performed in two steps. First each of the components modelled by the weather generator, namely the precipitation occurrence, the low and medium quantiles and high quantiles of precipitation intensity, are evaluated. In a second step all the components are evaluated together on a daily time-scale as well as on longer time-scales. Table 2 provides a summary of the occurrences’ evaluation. In general the occurrence ratio (WGEN/OBS) is close to 1, which shows a very good fit. The introduction of the covariates in the Markov model leads to a slight deterioration of the modelling of the highest quantiles occurrence at Westdorpe and a more significant deterioration at Gulu. In general the impact of this deterioration does not have much of an influence on the full model due to the relative low occurrence of these higher quantiles but it could impact precipitation return levels. Nevertheless at Gulu, the modelled low and moderate rain occurrence is more problematic, due to its regular occurrence, as it might result in an underestimation of precipitation if the intensity models are not compensating.

Table 2 Occurence ratio (WGEN/OBS) of precipitation occurrence averaged over 1,000 realizations

The calibration of the Gamma distribution leads to high correlation and low RMSE values (Fig. 4), showing good performance of this component of the weather generator. Higher values of the RMSE for Gulu can be explained by the higher range covered with the Gamma distribution at Gulu than at Westdorpe. A proportional difference will therefore lead to a higher RMSE.

Fig. 4

Quantile-quantile plots of the observed precipitation against the output of the model based on the gamma distribution for both Westdorpe (a) and Gulu (b). Both the WGEN-WOC (without covariates) (red) and the WGEN-WC (with covariates) (blue) are displayed

The GP distribution is also showing good performance (Fig.  5) although a bit deteriorated compared to the Gamma distribution. Westdorpe carries a too heavy tail while Gulu a too light one. A subjective modification of the shape parameter could correct for this defect but it was decided to keep the method entirely objective. In addition, it was expected that the GP distribution would be deteriorated compared to the Gamma one, as the variability in extreme precipitation is very high due to its stochastic nature. The introduction of covariates is significantly improving the model showing that covariates contribute to explain part of the variability inherent to extreme precipitation.

Fig. 5

Quantile-quantile plots of the observed precipitation against the output of the model based on the GP distribution for both Westdorpe (a) and Gulu (b). Both the WGEN-WOC (without covariates) (red) and the WGEN-WC (with covariates) (blue) are displayed

After evaluating each component of the weather generator, an evaluation is performed on the weather generator as a whole. This evaluation is performed on different time-scales to assess the ability of the model to reproduce the rapidly and slowly varying features that characterize the observations. To ease this assessment, time-series (T-RAN) are created by randomizing the observed daily values, thus with absence of rapidly and slowly varying features. Figure 6 shows the weather generators outputs without and with covariates (WGEN-WOC and WGEN-WC respectively) as well as the T-RAN in quantile plots for time-scales of 1, 5, 30 and 365 days. For the 1 and 5 days time-scales, all WGEN show good performances; The RMSE is lower than 1 mm for all models. Generally the T-RAN RMSE is twice as large as the RMSE of almost all the WGEN. The lowest quantiles are overestimated while the highest quantiles are underestimated in T-RAN. This shows that the rapidly varying features derived from the observations are already crucial to represent well the 5 days average precipitation quantiles. However the difference is small between the two weather generators showing that the implementation of covariates does not have a clear benefit at these small time-scales.

For the 30 days time-scale, results strongly differ for the two stations. This is due to the difference in the seasonal variation, strong at Gulu and weak at Westdorpe. Indeed at Westdorpe the differences between the two weather generators remain small. On the contrary, at Gulu the RMSE in precipitation quantiles of the WGEN-WOC is doubled compare to the RMSE of the WGEN-WC. The quantiles, again, are overestimated for the lowest quantiles and underestimated for the highest quantiles for WGEN-WOC. For the 365 days precipitation average, the models show similar performances indicating that neither the influence of the rapidly varying feature nor the slowly varying ones are significantly improving the representation of annual rainfall depths.

Fig. 6

Quantile-quantile plots of precipitation for the stations Westdorpe (a, c and e) and Gulu (b, d and f). a and b show the performance of the weather generator on the daily time-scale. c and d, e and f and g and h are showing similar performance on respectively a 5, 30 and 365 days time-scale. The WGEN-WOC (without covariates) are shown in red, the WGEN-WC (with covariates) are in blue and the T-RAN (randomized observed time-series) are in green

3.3 Climate variability

Based on the WGEN-WC results (1,000 synthetic time-series), the influence of the slowly and rapidly varying features on the climate statistics has been studied. To do so a statistic at the time $t$ is derived based on the values temporally located before or on time $t$ for each time-series. For a given synthetic time-series $j$, the average of a variable $X$ between the start of the time-serie and time $t$ is given by:

$$\begin{aligned} \bar{X}_{j}(t)=\frac{1}{N(t)} \mathop {\sum \limits _{i=1}^{N(t)}} X_{j}(i) \end{aligned}$$

(9)

where $N(t)$ is the number of samples such that $N(t)=t/\delta t$ with $\delta t$ being the time-scale at which the statistics is computed. Figure 7 shows this statistic applied to each synthetic time-series. Previous findings that the covariates have a stronger influence at Gulu than at Westdorpe are confirmed. While at Westdorpe the median of these 1,000 realizations stays more or less constant, the one at Gulu is strongly varying. This suggests that when deriving climate statistics, the period that is accounted for should be chosen with care. Figure 7 also shows the observed realization. For both locations the latter stays within the $2\sigma$ envelope but is not always close to the median. This fact brings confidence in the ability of the method to describe the climate variability correctly. In this paper the $2\sigma$ envelope is used to describe the uncertainty inherent to using a limited time-period to derive a climatology. In the rest of this paper we refer to this uncertainty as $\epsilon (t)$.

Fig. 7

Averaged values of precipitation amount ($\bar{X}(t)$) between the start of the time-serie and time t for 1,000 realizations of the WGEN-WC. Both location, namely Westdorpe (a) and Gulu (b), are shown. The median of all realizations (blue) as well as their $2\sigma$ envelope (red) are plotted. The observed realization (green) is also shown

Figure 8 shows a similar statistics than $\bar{X}(t)$ but for the 10-year precipitation return level. The presence of numerous peaks shows the high sensitivity of the derivation of 10-year precipitation return levels to elements of the time-series. However the realizations’ median is rather stable. In Fig. 8, for the longest time period, it can be noticed that although the realizations’ median is close to the observation in Westdorpe, the WGEN-WC overestimates the 10-year precipitation return levels by almost 20 mm in Gulu. This overestimation had already been pointed out during the evaluation of the WGEN in Sect. 3.2.

Fig. 8

Similar as Fig. 7 but for the 10-year precipitation return values

The spread of this envelope is represented in Fig. 9a for both locations. Both lines are very close to each other, suggesting that the way the uncertainty is derived is not really affected by the slowly varying signal but more by the stochasticity of the rapidly varying signal. A similar conclusion is drawn for the 10-year return levels uncertainty (Fig. 9b). From Fig. 9 it can be deduced that using a 30-year period induced an uncertainty of about 11 % and about 37 % when deriving respectively the average and the 10-year precipitation return level. Similar values were found when using WGEN-WOC instead of WGEN-WC (not shown). When deriving similar values using the T-RAN time-series instead of the WGEN-WC ones, the uncertainty values go down to 6 and 25 % respectively (not shown). This shows that using a WGEN based method and not a simple re-sampling method is essential to provide a good estimate of $\epsilon (t)$.

Fig. 9

Uncertainty $\epsilon (t)$ related to using a limited time-period at Gulu and Westdorpe for both averaged precipitation (a) and 10-year precipitation return level (b)

4 Discussion

4.1 The effect of the phase of the covariates

It is common practice to quantify climate change by substracting the 30-year climatology at the end of the 20th century (1970–1999) from the twenty-first century climatology (2070–2099). In order to assess the uncertainty $\epsilon (t)$ for such applications, a modification of the weather generator framework is necessary. After all, in the framework presented above, the time variant covariates are strictly identical in each synthetic time-series. This assumption does not hold when comparing future climatology with present-day climatology. To be able to derive $\epsilon (t)$ for these applications, it is required to unsynchronize the covariates in between time-series. As most climate analyses are performed on time-scale longer than a year, only the covariates referred to as inter-annual are unsynchronized. This is performed by generating covariates through the phase scrambling method (Theiler et al. 1992; Franzke 2012a, b). The phase scrambling method can be used to generate synthetic covariates with a power spectra similar to the original signal but with a randomized phase spectra. For more details please refer to (Theiler et al. 1992). The resulting synthetic covariates are, therefore, characterized by a period similar to the original covariates and are unsynchronized. With this new model, referred to as WGEN-WC-RS, 1,000 synthetic time-series have been generated (Fig. 10). Compared to Fig. 7b there is no local maximum at around 10 years anymore in the time-series median (in blue). The values of $\epsilon (t)$ derived from WGEN-WC-RC time-series are shown in Fig. 11.

Fig. 10

Averaged values of precipitation amount on a given period for a 1,000 realizations of the WGEN-WC for Gulu. The median of all realizations (blue) as well as their $2\sigma$ envelope (red) are plotted. The observed realization (green) is also shown

Fig. 11

Uncertainty $\epsilon (t)$ related to using a limited time-period at Gulu and Westdorpe for both averaged precipitation (a) and 10-year precipitation return level (b). Continuous lines are used or the WGEN-WC (with covariates) output and dotted lines for the WGEN-WC-RS (with shifted covariates)

Westdorpe’s WGEN-WC-RS $\epsilon (t)$ hardly differ from the one of the WGEN-WC due to the weak influence of the inter-annual covariates on the observation. On the contrary $\epsilon (t)$ for 30 years period in Gulu is increased by a factor of 1.25 when using WGEN-WC-RS instead of WGEN-WC. This factor increases with the time averaged period implying that longer periods are necessary to keep $\epsilon (t)$ unchanged in Gulu compared to Westdorpe. For example, when deriving precipitation averages in Gulu, a period of 20 years is needed to have a similar uncertainty compared to a 10-year period in Westdorpe. There is no significant difference in using WGEN-WC-RS instead of WGEN-WC for 10-years precipitation return levels (Fig. 11b). This is due to the low impact of inter-annual covariates on the higher quantiles of precipitation.

4.2 Implication for GCMs and RCMs

Climate modellers perform sensitivity analyses based on GCMs or regional climate models (RCMs). Although these models reproduce both the observed rapidly and slowly varying features, the slowly varying features are not always in phase with the observed ones. Of course components such as the seasonal cycle, the solar cycle or trends are in phase as they come from forcings external to the model. Nevertheless some inter-annual signal such as the ENSO or the NAO (Osborn et al. 1999), although being well reproduced, are not in phase with observations. As there was no known externally forced signal in the inter-annual covariates, the $\epsilon (t)$ inherent to using a limited period of GCMs output is similar to the one derived in Sect. 4.1.

5 Conclusion

This paper evaluates different methods to retrieve the uncertainty $\epsilon (t)$ related to deriving climate statistics from series which are limited in time. Different models were introduced that are able to reproduce none (T-RAN), part (rapidly varying—WGEN-WOC), or the whole components (rapidly and slowly varying—WGEN-WC) present in observations. In order to extract the slowly varying components the EMD has been modified to increase the robustness and to improve the significance assessment of AIMFs.

This method has been applied to a western European station (Westdorpe) and an eastern African one (Gulu). It was found that the improved EEMD produces physically consistent results with notably the presence of a seasonal cycle for both stations as well as some sub-seasonality ones in Gulu. In Westdorpe, a signal that was found to have a similar frequency as the NAO was also extracted. For both locations trends were identified.

The evaluation of the weather generator shows the ability of the models to reproduce similar sequences of precipitation events. It was found that although the WGEN-WOC is able to correctly reproduce daily precipitation quantiles, it is not able to correctly reproduce monthly averaged quantiles at Gulu. This deficiency was removed when implementing covariates in the weather generator framework.

Using the synthetic time-series derived from the WGEN-WC, it was found that the uncertainty, inherent to using a 30-year period, is 11 % for mean precipitation and 37 % for 10-year return levels. Randomized time-series (T-RAN) substantially underestimate $\epsilon (t)$ compared to the weather generator. When comparing different climatological periods, a modification to WGEN-WC was found to be necessary in order to relax the assumption that the time-varying covariates are strictly identical in each synthetic time-series. This improved weather generator (WGEN-WC-RS) is more sensitive to the presence of inter-annual pseudo-cycles in the observations and consequently $\epsilon (t)$ for mean precipitation increases at Gulu from 11 to 15 %. The uncertainty $\epsilon (t)$ in both average precipitation and 10-year return levels is substantial and should be taken into account when presenting climate projections for the future, which are based on limited time periods.

Appendix

In this appendix, the method used to combine the two Markov models, namely the HnMM2 and the NH2MM3, is described and illustrated (Fig. 12). After using likelihood estimations to calibrate separately these two models, namely the HnMM2 and the NH2MM3, they are combined to build a non-homogeneous nth order Markov model with 3 states (NHnMM3). The combination is performed by using the following calculations for each time-step t:

$$\begin{aligned} P^{NHnMM3}_{abcd->1}(t)=P^{HnMM2}_{abcd->1}\frac{P^{NH2MM3}_{d->1}(t)}{P^{HnMM2}_{d->1}}\end{aligned}$$

(10)

$$\begin{aligned} P^{NHnMM3}_{abcd->2}(t)=P^{HnMM2}_{abcd->2}\frac{P^{NH2MM3}_{d->2}(t)}{P^{HnMM2}_{d->2}}\end{aligned}$$

(11)

$$\begin{aligned} P^{NHnMM3}_{abcd->3}(t)=P^{HnMM2}_{abcd->2}\frac{P^{NH2MM3}_{d->3}(t)}{P^{HnMM2}_{d->2}} \end{aligned}$$

(12)

where $a, b, c, d$ represent respectively the time-step t-1, t-2, t-3, t-4 and can take any value from 1 to 3.

$$\begin{aligned} P^{NHnMM3}_{abci->j}(t)=P^{NHnMM3}_{a'b'c'i->j}(t) \end{aligned}$$

(13)

where $a, b, c, a', b'$ and $c'$ can take independently a value of 2 or 3 while $i$ and $j$ can take any values. This example illustrates the combination with a 4rd order markov model but it is valid for any order, taken by HnMM2.

Fig. 12

Illustration of an example of combination of the two models HnMM2 and NH2MM3. States are indicated with numbers ranging from 1 to 3 which respectively refer to no precipitation, precipitation above 0 and lower than TR95 and precipitation above TR95. Straight arrows indicate a homogeneous relation and wavy arrows a non-homogeneous one