1 Introduction

During the last decade, ensembles of dynamical downscaling climate simulations have been increasingly used to better understand our evolving climate at scales that are not resolved by global climate models (GCM). Despite their limited area of integration, regional climate models (RCM) are now commonly used to downscale climate-change projections from GCM. Regional models, as well as global models, are sensitive to initial conditions (IC) due to the chaotic character of the climate system. In an ensemble of simulations performed with a given RCM driven by the same external boundary conditions, but launched from different IC, individual simulations evolve into different weather sequences. The spread of the ensemble’s members around the ensemble mean (EM) provides a quantitative measure of internal variability (IV) in RCM simulations, which will influence the estimates of uncertainty in downscaling climate simulations and projections. Therefore, it seems relevant to pay a particular attention on statistics of IV in ensembles of RCM simulations.

Numerous previous studies have demonstrated the presence of internal variability (IV) in ensembles of nested RCM simulations (e.g., Giorgi and Bi 2000; Weisse et al. 2000; Rinke and Dethloff 2000; Christensen et al. 2001; Caya and Biner 2004; Rinke et al. 2004; Lucas-Picher et al. 2004; Alexandru et al. 2007; de Elía et al. 2008; Lucas-Picher et al. 2008; Nikiéma and Laprise 2011a, b). IV is defined as the inter-member spread between members in an ensemble of simulations performed by a given RCM driven by identical lateral boundary conditions (LBC), where different members are being initialised at different times. In autonomous coupled atmosphere–ocean global climate models (AOGCM), IV is equivalent to natural, transient-eddy variability (TV) under steady forcing, in the limit of long simulations and large ensembles, owing to the ergodicity property (i.e. time and ensemble averages should all be equal). In the context of nested models, it is important to distinguish IV and TV because the ergodicity property is violated due to the control exerted by LBC. Possibly a better name for IV that avoids all ambiguity is that of “inter-member variability”. In the following, the abbreviation IV will be referring to inter-member variability.

Recent work has been undertaken to further our understanding of the physical mechanisms responsible for the maintenance of IV in nested RCM simulations despite the control exerted by LBC, and the intermittent nature of IV fluctuations. Working under the hypothesis that episodes of rapid growth of IV coincide with hydrodynamic instabilities of the flow, Diaconescu et al. (2012) have used singular vector (SV) to analyse an ensemble simulations of the fifth-generation Canadian RCM (CRCM5) over North America. They found that a large part of the IV growth could be explained by the rapid growth of initially small amplitude perturbations represented by a set of the ten leading (i.e. most unstable) SVs. They also found a high similarity between the structure of the first SV after 24–36 h of the tangent-linear model integration and the IV disturbances in the CRCM5 simulation, the vertical structure of this SV revealing that baroclinic conversion is the dominant process in the IV growth.

Nikiéma and Laprise (2011a, b) established detailed prognostic equations for inter-member variance (\( \partial \sigma^{2}_{IV} /\partial t \)) of various atmospheric variables such as potential temperature and vorticity. They applied these equations to perform diagnostic budget studies to quantify the various dynamical and diabatic contributions to the time variations of IV that took place in an ensemble of 20 simulations of the third-generation Canadian RCM (CRCM3) that differed only in their IC. Results show that the dominant terms responsible for the rapid increases of IV are either the covariance term involving inter-member fluctuations of temperature and diabatic heating, or covariance of inter-member fluctuations acting upon ensemble-mean gradients. By far the dominant term responsible for decreases of IV is that of transport of \( \sigma^{2}_{IV} \) by the ensemble-mean flow out of the domain. Although \( \sigma^{2}_{IV} \) greatly fluctuates in time, there is no long-term trend. In a time-averaged sense, the IV budget equation reduces to a balance between generation and destruction terms. Nikiéma and Laprise (2011b) noted that the dominant terms in the \( {{\partial \sigma^{2}_{IV} } \mathord{\left/ {\vphantom {{\partial \sigma^{2}_{IV} } {\partial t}}} \right. \kern-0pt} {\partial t}} \) equation tend to contribute systematically (either positively or negatively) throughout the troposphere and most of the time. A noteworthy result from these studies is that there appears to be an undeniable parallel between the energetics of IV in ensemble simulations of nested model and the energy conversions taking place in weather systems, with generation of potential energy by diabatic processes such as condensation, convection and radiation, and later conversion to kinetic energy (e.g., Lorenz 1955, 1967). This led the authors to conclude that RCM IV is a natural phenomenon arising from the chaotic nature of the atmosphere, and not a numerical artefact associated, for example, to the nesting technique.

The motivation of this paper is to pursue further the possibility of establishing a close parallel between the energy conversions associated with time fluctuations of IV in ensemble simulations of RCM and the energy conversions taking place in weather systems. Inspired by the classical work of Lorenz (1955, 1967) for global energetics of weather systems, we aimed at a formulation of an energy cycle for IV that would be applicable for limited-area domain. Pearce (1978) and later Marquet (1991, 1994, 2003a, b) had developed a general conceptual framework for local energy cycle that provided the sought formalism. In this paper, the prognostic equations for ensemble-mean kinetic energy and available enthalpy are decomposed into contributions due to ensemble-mean variables (EM) and those due to deviations from the ensemble mean (IV), which leads to an energy cycle for inter-member variability in ensemble simulations of RCM.

The paper is structured as follows. In Sects. 2 and 3, we review the basic field equations and the different forms of energy in the atmospheric system, respectively. Then in Sect. 4, we establish tendency equations for EM and IV contributions to kinetic energy and available enthalpy. In Sect. 5, an energy cycle is built by linking the various contributions to exchanges between the energy reservoirs, and physical interpretations are discussed. Finally conclusions are given in Sect. 6. Symbols and notations are explained in “List of symbols”.

2 Basic equations in the atmospheric system

The equations that form the basis of atmospheric component of climate models describe the time evolution and spatial structure of different atmospheric variables at scales that are resolved by the computational mesh. The momentum, thermodynamics and continuity equations express the principles of conservation of momentum, energy and mass, respectively. A diagnostic relation for the hydrostatic equilibrium and the state law for an ideal gas complete the primitive equations. Using pressure \( \left( p \right) \) as vertical coordinate and a local Cartesian system \( \left( {x,y} \right) \) aligned with latitude \( \left( \varphi \right) \) and longitude \( \left( \lambda \right) \), these equations can be written under the traditional approximation (e.g., Holton 2004) as follows:

$$ \frac{{\partial \overrightarrow {V} }}{\partial t} + \overrightarrow {V} \cdot \overrightarrow {\nabla } \overrightarrow {V} + \omega \frac{{\partial \overrightarrow {V} }}{\partial p} + f\hat{k} \times \overrightarrow {V} + \overrightarrow {\nabla } \Upphi - \overrightarrow {F} = 0 $$
(1)
$$ \frac{\partial T}{\partial t} + \overrightarrow {V} \cdot \overrightarrow {\nabla } T + \omega \frac{\partial T}{\partial p} - \frac{\omega \alpha }{{C_{p} }} - \frac{Q}{{C_{p} }} = 0 $$
(2)
$$ \overrightarrow {\nabla } \cdot \overrightarrow {V} + \frac{\partial \omega }{\partial p} = 0 $$
(3)
$$ \frac{\partial \Upphi }{\partial p} + \alpha = 0 $$
(4)
$$ \alpha - \frac{RT}{p} = 0 $$
(5)

where \( \overrightarrow {V} \left( {u,v} \right) \) is the horizontal wind vector with components \( u = a\cos \varphi d\lambda /dt \) and \( v = ad\varphi /dt \), and \( \omega = dp/dt \) is the pressure-coordinate vertical motion. The operators \( \frac{\partial }{\partial t} \) and \( \overrightarrow {\nabla } \) are respectively the local time derivative and the lateral gradient, both taken along constant pressure surfaces (vectors operations in spherical coordinates are given in “Appendix 1”). All symbols have their standard meaning: \( a \) is the average Earth radius, \( f = 2\Upomega \sin \varphi \) is the Coriolis parameter, \( \Upomega \) is the Earth’s rotation rate, \( \Upphi = gz \) is the geopotential height, \( z \) is the altitude, \( \overrightarrow {F} \) is horizontal momentum sources/sinks, \( T \) is the air temperature, \( Q \) is the total diabatic heating rate, \( C_{p} \) is the specific heat at a constant pressure and \( R \) is the gas constant for dry air.

3 The atmospheric energy equations

In the atmospheric system expressed in pressure coordinate, the basic forms of energy are naturally the specific kinetic energy \( K = \vec{V}\cdot\vec{V}/2 \) and specific enthalpy \( H = C_{p} T \) (the term specific will henceforth be omitted to lighten the terminology). The kinetic energy equation is obtained by taking the following operations:

$$ \overrightarrow {V} \cdot \left( {{\text{Eq}}.\,1} \right) + \left( {K + \Upphi } \right)\left( {{\text{Eq}}.\,3} \right) + \omega \left( {{\text{Eq}}.\,4} \right) $$

resulting in the following equation (as detailed in “Appendix 2”):

$$ \frac{\partial K}{\partial t} + \overrightarrow {\nabla } \cdot \left[ {\left( {K + \Upphi } \right)\overrightarrow {V} } \right] + \frac{{\partial \left[ {\left( {K + \Upphi } \right)\omega } \right]}}{\partial p} + \omega \alpha - \overrightarrow {V} \cdot \overrightarrow {F} = 0 $$
(6)

The enthalpy equation is readily obtained by taking the following operation:

$$ C_{p} \left[ {\left( {{\text{Eq}}.\,2} \right) + T\left( {{\text{Eq}}.\,3} \right)} \right] $$

which gives

$$ \frac{{\partial \left( {C_{p} T} \right)}}{\partial t} + \overrightarrow {\nabla } \cdot \left( {C_{p} T\overrightarrow {V} } \right) + \frac{{\partial \left( {C_{p} T\omega } \right)}}{\partial p} - \omega \alpha - Q = 0 $$
(7)

Once integrated over the entire atmospheric column, the sum of kinetic energy (6) and enthalpy (7) equations expresses the change of the total energy, defined as \( K + C_{p} T \):

$$ \frac{{\partial \left( {K + C_{p} T} \right)}}{\partial t} + \overrightarrow {\nabla } \cdot \left[ {\left( {K + \Upphi + C_{p} T} \right)\overrightarrow {V} } \right] + \frac{{\partial \left[ {\left( {K + \Upphi + C_{p} T} \right)\omega } \right]}}{\partial p} - \overrightarrow {V} \cdot \overrightarrow {F} - Q = 0 $$
(8)

Upon global averaging over the entire atmosphere, noted as \( \left\{ {} \right\} \), and with suitable lower boundary conditions (e.g. eq. 2.12 and 2.16 of Laprise and Girard 1990), the celebrated result of atmospheric energetics obtains:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\partial \left\{ K \right\}}}{\partial t} + \left\{ {\omega \alpha } \right\} - \left\{ {\overrightarrow {V} \cdot \overrightarrow {F} } \right\} = 0} \hfill \\ {\frac{{\partial \left\{ {C_{p} T} \right\}}}{\partial t} - \left\{ {\omega \alpha } \right\} - \left\{ Q \right\} = 0} \hfill \\ {\frac{{\partial \left\{ {K + C_{p} T} \right\}}}{\partial t} - \left\{ {\overrightarrow {V} \cdot \overrightarrow {F} } \right\} - \left\{ Q \right\} = 0} \hfill \\ \end{array} } \right. $$
(9)

The last equation expresses conservation of global total energy \( \left\{ {K + C_{p} T} \right\} \) in the absence of net external sources/sinks of mechanical energy \( \left\{ {\overrightarrow {V} \cdot \overrightarrow {F} } \right\} \) and diabatic heat \( \left\{ Q \right\} \). Hence \( \{ {\omega \alpha } \} \) represents a conversion between kinetic energy and enthalpy (e.g., Lorenz 1967; Peixoto and Oort 1992).

In energetics studies it is useful to decompose the terms appearing in the budget equations into contributions from some mean and deviations thereof, where the mean may be either an average taken over time, around a latitude circle or, as will be the case in this paper, the average of the members in an ensemble of nested model simulations. For quadratic terms such as kinetic energy in (6), the decomposition leads to separate contributions from mean winds and from deviation winds. The same decomposition applied to linear terms such as enthalpy in (7), however, does not bring out any apparent contribution from deviations upon averaging and hence it is not possible to clearly identify contributions from mean and deviations in exchanges between kinetic and thermodynamic energies (e.g., Boer 1989). This and the fact that enthalpy appears to be overwhelmingly large compared to kinetic energy for typical atmospheric states, makes it advantageous to modify (7) in order to operate as deviation from some reference state, thus reducing the magnitude of the thermodynamic energy contribution. Casting the thermodynamic equation in a quadratic (or some other nonlinear) form also allows decomposing into contributions from mean and deviations.

The most widely used approach for global energetics is that pioneered by Lorenz (1955, 1967) of using the concept of available potential energy (APE). APE has the advantage of being a much smaller quantity than enthalpy and a positive definite quantity. It requires however defining a minimum potential energy reference state that can only be established globally, and “APE is a global concept defined for a system as a whole, not for a portion of it” (van Mieghem 1973, section 14.8); hence APE is not meaningful locally or over limited-area domains.

Following the approach of available potential energy described by Pearce (1978), Marquet (1991, 1994, 2003a, b) discussed the concept of locally defined available energy. He showed that the desired properties are obtained with using a variable called Available Enthalpy \( a_{h} = \left( {H - H_{r} } \right) - T_{r} \left( {S - S_{r} } \right) \) combining enthalpy \( H = C_{p} \left( {T - T_{r} } \right) + H_{r} \) and entropy \( S = C_{p} \ln \left( {\theta /\theta_{r} } \right) + S_{r} \), with \( T_{r} \), \( H_{r} \) and \( S_{r} \) three constants, and where \( \theta = T\left( {p_{oo} /p} \right)^{{R/C_{p} }} \) is the potential temperature, \( \theta_{r} = T_{r} \left( {p_{oo} /p_{r} } \right)^{{R/C_{p} }} \) is a constant with units of temperature and \( p_{r} \) a constant with units of pressure. An equation for \( a_{h} \) is thus obtained from the enthalpy and entropy equations

$$ \frac{dH}{dt} - \omega \alpha - Q = 0 $$
(10)
$$ \frac{dS}{dt} - \frac{Q}{T} = 0 $$
(11)

by taking the operation \( \left( {{\text{Eq}}.\,10} \right) - T_{r} \left( {{\text{Eq}}.\,11} \right) \), which gives

$$ \frac{{da_{h} }}{dt} - \omega \alpha - \left( {1 - \frac{{T_{r} }}{T}} \right)Q = 0 $$
(12)

A Lagrangian form of the kinetic energy equation may be obtained by taking the operation \( \overrightarrow {V} \cdot \left( {{\text{Eq}}.\,1} \right) + \omega \left( {{\text{Eq}}.\,4} \right) \):

$$ \frac{dK}{dt} + \overrightarrow {V} \cdot \overrightarrow {\nabla } \Upphi + \omega \frac{\partial \Upphi }{\partial p} + \omega \alpha - \overrightarrow {V} \cdot \overrightarrow {F} = 0 $$
(13)

Taking the sum \( \left( {{\text{Eq}}.\,12} \right) + \left( {{\text{Eq}}.\,13} \right) \) gives

$$ \frac{{d\left( {K + a_{h} } \right)}}{dt} + \left[ {\overrightarrow {V} \cdot \overrightarrow {\nabla } + \omega \frac{\partial }{\partial p}} \right]\Upphi - \overrightarrow {V} \cdot \overrightarrow {F} - \left( {1 - \frac{{T_{r} }}{T}} \right)Q = 0 $$
(14)

where the term \( [ {\overrightarrow {V} \cdot \overrightarrow {\nabla } + \omega \frac{\partial }{\partial p}} ]\Upphi \) represents fluxes of gravitational potential energy. The set (12)–(14) offers an alternative form to the conventional energy equations to (6)–(8) and to Lorenz APE. Compared to the conventional set, this set has the advantages that available enthalpy is a much smaller quantity than enthalpy and it is not a linear function of temperature, which will allow decomposing the energy cycle into contributions from the ensemble mean and deviations thereof, as we shall see shortly. Compared to Lorenz energy cycle based on APE that can only be applied globally, the set (12)–(14) is amenable to be applied on limited-area domains (e.g., Marquet 1994, 2003a, b).

Marquet (1991) pointed out that available enthalpy can be slit into separate contributions depending solely on temperature and pressure:

$$ a_{h} \left( {T,p} \right) = a_{T} \left( T \right) + a_{p} \left( p \right) $$
(15)

where

$$ a_{T} \left( T \right) = C_{p} T_{r} \left[ {\left( {\frac{{T - T_{r} }}{{T_{r} }}} \right) - \ln \left( {\frac{T}{{T_{r} }}} \right)} \right] $$
(16)

and

$$ a_{p} \left( p \right) = RT_{r} \ln \left( {\frac{p}{{p_{r} }}} \right) $$
(17)

The equation for \( a_{h} \) may be split into separate equations for \( a_{T} \) and \( a_{p} \) as follows:

$$ \frac{{da_{T} }}{dt} - \frac{R\omega }{p}\left( {T - T_{r} } \right) - \left( {1 - \frac{{T_{r} }}{T}} \right)Q = 0 $$
(18)
$$ \frac{{da_{p} }}{dt} - \frac{R\omega }{p}T_{r} = 0 $$
(19)

Equations (18) and (19), together with the kinetic energy equation (13), form a valid (and exact) local energy cycle system for hydrostatic flow; these are the pressure-coordinate equivalent of equations (14) of Marquet (1991). Alternatively Eqs. (18) and (19) may be cast in flux form using (3):

$$ \frac{{\partial a_{T} }}{\partial t} + \overrightarrow {\nabla } \cdot \left( {a_{T} \overrightarrow {V} } \right) + \frac{{\partial \left( {a_{T} \omega } \right)}}{\partial p} - \frac{R\omega }{p}\left( {T - T_{r} } \right) - \left( {1 - \frac{{T_{r} }}{T}} \right)Q = 0 $$
(18')
$$ \frac{{\partial a_{p} }}{\partial t} + \overrightarrow {\nabla } \cdot \left( {a_{p} \overrightarrow {V} } \right) + \frac{{\partial \left( {a_{p} \omega } \right)}}{\partial p} - \frac{R\omega }{p}T_{r} = 0 $$
(19')

We note that in pressure coordinates Eq. (19) is an identity since \( \frac{{\partial a_{p} }}{\partial t} = 0 \), \( \overrightarrow {\nabla } a_{p} = 0 \) and \( \frac{{\partial a_{p} }}{\partial p} = RT_{r} \frac{\partial }{\partial p}\ln p = \frac{{RT_{r} }}{p} \). It is noteworthy that, despite the fact that \( a_{p} \) is constant locally in pressure coordinates, its integral over a finite domain fluctuates as a result of changes in surface pressure \( p_{S} \):

$$ \begin{aligned} - \frac{1}{g}\frac{d}{dt}\int\limits_{{p_{S} }}^{{p_{T} }} {a_{p} dp} & = - \frac{{RT_{r} }}{g}\frac{d}{dt}\int\limits_{{p_{S} }}^{{p_{T} }} {\ln \frac{p}{{p_{r} }}dp} \\ & = - \frac{{RT_{r} }}{g}\frac{d}{dt}\left[ {p\ln \frac{p}{{p_{r} }} - p} \right[_{{p_{S} }}^{{p_{T} }} \\ & = \frac{{RT_{r} }}{g}\frac{d}{dt}\left[ {p_{S} \left( {\ln \frac{{p_{S} }}{{p_{r} }} - 1} \right)} \right] \\ \end{aligned} $$
(20)

Marquet (1991) noted that the constant \( p_{r} \) can be chosen so that the global average of the absolute value of \( a_{p} \) is zero; this is achieved by defining \( \ln\,p_{r} \) as the time and space average of \( \ln p \), which means that \( p_{r} \approx p_{oo} /e \) if \( p_{oo} \) is approximately the mean of \( p_{S} \).

Following Marquet (1991), the temperature-dependent component \( a_{T} \left( T \right) \) can be written as

$$ a_{T} \left( T \right) = C_{p} T_{r} \;\Im \left( \chi \right) $$
(21)

where

$$ \Im \left( \chi \right) = \chi - \ln \left( {1 + \chi } \right) $$
(22)

and

$$ \chi = \frac{{T - T_{r} }}{{T_{r} }} $$
(23)

It is noteworthy that the function \( \Im \left( \chi \right) \) is positive definite for \( \chi \)> -1, which corresponds to \( T > 0 \); this property is most valuable when working with available energy concepts. The constant \( T_{r} \) may be chosen to minimise the value of \( \chi \) over the domain of interest, as in Pearce (1978). Marquet (1991) proposed to define it such that \( T_{r}^{ - 1} \) corresponds to the time and space average of \( T^{ - 1} \) over the domain of interest, which would give \( T_{r} \approx 250\,{\text{K}} \) if integrated over the entire atmosphere. With this choice, the actual temperature generally deviates from \( T_{r} \) only by less than \( \pm 20\,\% \), and hence \( \chi \) is a small quantity. This allows approximating \( a_{T} \left( T \right) \) by series expansion around \( a_{T} \left( {T_{r} } \right) \), i.e. expand \( \Im \left( \chi \right) \) around \( \Im \left( 0 \right) \). Noting that \( \Im \left( 0 \right) = \Im^{\prime}\left( 0 \right) = 0 \) and \( \Im^{\prime \prime } \left( 0 \right) = 1 \), this gives to leading order

$$ a_{T} \left( T \right) \approx \frac{{C_{p} T_{r} }}{2}\;\left( {\frac{{T - T_{r} }}{{T_{r} }}} \right)^{2} $$
(24)

The positive-definite character of \( a_{T} \left( T \right) \) is maintained by the quadratic form under this approximation. The consequences of the small-\( \chi \) approximation on the thermodynamic equation are discussed in “Appendix 4”. Equations (13), (18) and (19), together with the definition (17) and the approximation (24), constitute an approximate set that can be used to establish an energy cycle (Pearce 1978; Marquet 1991) in terms of ensemble mean and deviations thereof, for ensembles of limited-area, regional climate simulations. In the next section, the approximate Eq. (24) will be used to establish the available enthalpy energy equations associated with EM and IV. It will be showed that the quadratic expression of \( a_{T} \) leads to an IV available-enthalpy that is proportional to the inter-member variance of temperature (\( \left\langle {T^{\prime 2} } \right\rangle \), e.g. Nikiéma and Laprise 2001a). This retains the conventional definition of IV and allows an immediate physical interpretation.

4 Ensemble-mean energy equations

An ensemble of simulations of an RCM will be analysed in terms of basic statistics such as ensemble mean and variance and covariance of deviations thereof. The statistics will be calculated from an archive of an ensemble of N-member simulations produced with the same nested model driven by identical LBC, but launched at different starting times; for instance, the initial conditions (IC) of two successive simulations will be shifted by 1 day. A representative ensemble-mean (EM) state, as well as deviations from the ensemble mean, can be computed from the member simulations in the ensemble. Thus, each atmospheric variable \( \Uppsi_{n} \in \left\{ {T_{n} ,\,u_{n} ,\,v_{n} ,\,\omega_{n} ,\,\Upphi_{n} ,\, \ldots } \right\} \) where \( n \) represents the index number of each simulation, will be split into ensemble-mean \( \left\langle \Uppsi \right\rangle \) and deviation \( \Uppsi^{\prime} \) components as

$$ \Uppsi = \left\langle \Uppsi \right\rangle + \Uppsi^{\prime} $$
(25)

where the ensemble-mean operator \( \left\langle {} \right\rangle \) is calculated as

$$ \left\langle \Uppsi \right\rangle = \frac{1}{N}\sum\limits_{n = 1}^{N} {\Uppsi_{n} } $$
(26)

and the deviations as

$$ \Uppsi^{\prime} = \Uppsi - \left\langle \Uppsi \right\rangle $$

with the property that \( \left\langle {\Uppsi^{\prime}} \right\rangle = 0 \). Without ambiguity, the index n is ignored to facilitate reading and writing of equations.

Quadratic quantities such as the product of two variables \( \psi \) and \( \chi \) can be decomposed as

$$ \psi \,\chi = \left\langle \psi \right\rangle \left\langle \chi \right\rangle + \left\langle \psi \right\rangle \chi^{\prime} + \psi^{\prime}\left\langle \chi \right\rangle + \psi^{\prime}\chi^{\prime} $$
(27)

so that

$$ \left\langle {\psi \,\chi } \right\rangle = \left\langle \psi \right\rangle \left\langle \chi \right\rangle + \left\langle {\psi^{\prime}\chi^{\prime}} \right\rangle $$
(28)

In particular, the ensemble-mean kinetic energy \( \left\langle K \right\rangle = \langle \overrightarrow {V} \cdot \overrightarrow {V} /2\rangle \) can be decomposed into two components as follows:

$$ \left\langle K \right\rangle = K_{EM} + K_{IV} $$
(29)

where \( K_{EM} = \langle \overrightarrow {V} \rangle \cdot \langle \overrightarrow {V} \rangle /2 \) is the kinetic energy of the ensemble-mean wind and \( K_{IV} = \langle \overrightarrow {{V^{\prime}}} \cdot \overrightarrow {{V^{\prime}}} \rangle /2 \) is ensemble-mean kinetic energy of the deviation winds. Similarly, using the quadratic approximation to the temperature component \( a_{T} \) of available enthalpy, its ensemble mean \( A = \langle a_{T} \rangle \) can be decomposed as

$$ A = A_{EM} + A_{IV} $$
(30)

where \( A_{EM} = \frac{{C_{p} }}{{2T_{r} }}\langle T - T_{r} \rangle^{2} \) and \( A_{IV} = \frac{{C_{p} }}{{2T_{r} }}\langle T^{\prime 2} \rangle \) (see “Appendix 3” for details).

It can be noted that \( A_{IV} \) is proportional to the inter-member variance (\( \sigma^{2}_{IV} \)) for the temperature (Nikiéma and Laprise 2001a). Unlike the exact formulation of \( a_{T} \) (Eq. 21), the quadratic expression leads to convenient definitions of AEM and AIV, which are proportional to \( \langle T\rangle^{2} \) and \( \langle T^{\prime 2} \rangle \), respectively.

The ensemble-mean equations for kinetic energy and available enthalpy are readily obtained by applying the operator \( \langle \rangle \) on (6), (18') and (19'):

$$ \frac{\partial \langle K\rangle }{\partial t} + \overrightarrow {\nabla } \cdot \left\langle {\left( {K + \Upphi } \right)\overrightarrow {V} } \right\rangle + \frac{\partial }{\partial p}\left\langle {\left( {K + \Upphi } \right)\omega } \right\rangle + \frac{R}{p}\langle \omega T\rangle - \left\langle {\overrightarrow {V} \cdot \overrightarrow {F} } \right\rangle = 0 $$
(31)
$$ \frac{{\partial \langle a_{T} \rangle }}{\partial t} + \overrightarrow {\nabla } \cdot \left( {\left\langle {a_{T} \overrightarrow {V} } \right\rangle } \right) + \frac{{\partial \left( {\left\langle {a_{T} \omega } \right\rangle } \right)}}{\partial p} - \frac{R}{p}\left\langle {\omega \left( {T - T_{r} } \right)} \right\rangle - l\left\langle {\left( {\frac{{T - T_{r} }}{{T_{r} }}} \right)Q} \right\rangle = 0 $$
(32)
$$ \frac{{\partial \left\langle {a_{p} } \right\rangle }}{\partial t} + \overrightarrow {\nabla } \cdot \left( {\left\langle {a_{p} \overrightarrow {V} } \right\rangle } \right) + \frac{{\partial \left( {\left\langle {a_{p} \omega } \right\rangle } \right)}}{\partial p} - \frac{{RT_{r} }}{p}\left\langle \omega \right\rangle = 0 $$
(33)

where \( l \) in (32) is a factor of order unity (details are provided in “Appendix 4”).

These equations embody the approximate energetics applicable to an ensemble of regional climate model simulations. We now proceed in separating ensemble-mean kinetic energy and enthalpy into components resulting of the ensemble-mean variables and components resulting of covariances of deviations from the ensemble mean. This will reveal the physical processes responsible for conversions from one type of energy to another.

4.1 Kinetic energy equations for \( K_{EM} \) and \( K_{IV} \)

The kinetic energy equation for the ensemble-mean wind (\( K_{EM} \)) is obtained by taking the following operation:

$$ \left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {{\text{Eq}}.\,1} \right\rangle + \left( {K_{EM} + \left\langle \Upphi \right\rangle } \right)\left\langle {{\text{Eq}}.\,3} \right\rangle + \left\langle \omega \right\rangle \left\langle {{\text{Eq}}.\,4} \right\rangle + \left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {\overrightarrow {{V^{\prime}}} \left( {{\text{Eq}}.\,3 - \left\langle {{\text{Eq}}.\,3} \right\rangle } \right)} \right\rangle $$

After a few rearrangements (see details in “Appendix 5”), the following equation is obtained:

$$ \frac{{\partial K_{EM} }}{\partial t} = C_{EM} - C_{K} - D_{EM} - F_{{K_{EM} }} - H_{{K_{EM} }} $$
(34)

where

$$ \begin{aligned} K_{EM} & = \langle \overrightarrow {V} \rangle \cdot \langle \overrightarrow {V} \rangle /2 \\ C_{EM} & = - \left\langle \omega \right\rangle \left\langle \alpha \right\rangle \\ C_{K} & = - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \left( {\overrightarrow {{V^{\prime}}} \cdot \overrightarrow {\nabla } } \right)\left\langle {\overrightarrow {V} } \right\rangle } \right\rangle - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \left( {\omega^{\prime}\frac{{\partial \left\langle {\overrightarrow {V} } \right\rangle }}{\partial p}} \right)} \right\rangle \\ D_{EM} & = - \left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {\overrightarrow {F} } \right\rangle \\ F_{{K_{EM} }} & = \overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle K_{EM} } \right) + \frac{\partial }{\partial p}\left( {\left\langle \omega \right\rangle K_{EM} } \right) \\ H_{{K_{EM} }} & = \overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {\overrightarrow {{V^{\prime}}} \overrightarrow {{V^{\prime}}} } \right\rangle } \right) + \overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle \left\langle \Upphi \right\rangle } \right) \\ & \quad + \frac{\partial }{\partial p}\left( {\left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {\overrightarrow {{V^{\prime}}} \omega^{\prime}} \right\rangle } \right) + \frac{\partial }{\partial p}\left( {\left\langle \omega \right\rangle \left\langle \Upphi \right\rangle } \right) \\ \end{aligned} $$

The kinetic energy equation due to the wind deviations from the ensemble mean, \( \left( {K_{IV} } \right) \), can be established by considering the definition \( K_{IV} = \left\langle K \right\rangle - K_{EM} \) to calculate \( \left( {{\text{Eq}}.\,31} \right) - \left( {{\text{Eq}}.\,34} \right) \). After a few manipulations (details are provided in “Appendix 6”), and noting that \( \left\langle {K\overrightarrow {V} } \right\rangle - K_{EM} \left\langle {\overrightarrow {V} } \right\rangle = K_{IV} \left\langle {\overrightarrow {V} } \right\rangle + \left\langle {K\overrightarrow {{V^{\prime}}} } \right\rangle \), we get

$$ \frac{{\partial K_{IV} }}{\partial t}{\text{ = C}}_{IV} {\text{ + C}}_{K} - D_{IV} - F_{{K_{IV} }} - H_{{K_{IV} }} $$
(35)

where

$$ \begin{aligned} K_{IV} & \equiv \left\langle k \right\rangle ,\quad k = \overrightarrow {{V^{\prime}}} \cdot \overrightarrow {{V^{\prime}}} /2 \\ C_{IV} & = - \left\langle {\omega^{\prime}\alpha^{\prime}} \right\rangle \\ C_{K} & = - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \left( {\overrightarrow {{V^{\prime}}} \cdot \overrightarrow {\nabla } } \right)\left\langle {\overrightarrow {V} } \right\rangle } \right\rangle - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \left( {\omega^{\prime}\frac{{\partial \left\langle {\overrightarrow {V} } \right\rangle }}{\partial p}} \right)} \right\rangle \\ D_{IV} & = - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \overrightarrow {{F^{\prime}}} } \right\rangle \\ F_{{K_{IV} }} & = \overrightarrow {\nabla } \cdot \left[ {K_{IV} \left\langle {\overrightarrow {V} } \right\rangle } \right] + \frac{{\partial \left( {K_{IV} \left\langle \omega \right\rangle } \right)}}{\partial p} \\ H_{{K_{IV} }} & = \overrightarrow {\nabla } \cdot \left\langle {\left( {k + \Upphi^{\prime}} \right)\overrightarrow {{V^{\prime}}} } \right\rangle + \frac{{\partial \left\langle {\left( {k + \Upphi^{\prime}} \right)\omega^{\prime}} \right\rangle }}{\partial p} \\ \end{aligned} $$

4.2 Equations for the temperature-dependent part of available enthalpy \( A_{EM} \) and \( A_{IV} \)

It was established in (24) that the ensemble-mean of the part of available enthalpy arising from temperature only is a positive-definite field \( A = \left\langle {a_{T} } \right\rangle \) that could be split in a contribution \( A_{EM} \) arising from ensemble-mean temperature \( \left\langle T \right\rangle \) and a contribution \( A_{IV} \) arising from the deviations \( T^{\prime} \) of temperature from the ensemble-mean value, as in (30).

The prognostic equation for \( A_{EM} \) is obtained by taking the operation \( \frac{{\left\langle {T - T_{r} } \right\rangle }}{{T_{r} }}\left\langle {{\text{Eq}}.\,7} \right\rangle \), which gives after some approximations

$$ \frac{{\partial A_{EM} }}{\partial t} = G_{EM} + I_{AB} - C_{EM} - C_{A} - F_{{A_{EM} }} - H_{{A_{EM} }} $$
(36)

where

$$ \begin{aligned} A_{EM} & = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T_{*} } \right\rangle^{2} ,\quad T_{*} = T - T_{r} \\ G_{EM} & = \frac{l}{{T_{r} }}\left\langle {T_{*} } \right\rangle \left\langle Q \right\rangle \, \\ C_{EM} & = - \left\langle \omega \right\rangle \left\langle \alpha \right\rangle \\ C_{A} & = - \left\langle {\overrightarrow {V}^{\prime } \frac{{T^{\prime } }}{{T_{r} }}} \right\rangle \cdot \overrightarrow {\nabla } \left\langle {C_{p} T} \right\rangle - \left\langle {\omega^{\prime}\frac{{T^{\prime } }}{{T_{r} }}} \right\rangle \frac{{\partial \left\langle {C_{p} T} \right\rangle }}{\partial p} \\ F_{{A_{EM} }} & = \overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle A_{EM} } \right) + \frac{{\partial \left( {\left\langle \omega \right\rangle A_{EM} } \right)}}{\partial p} \\ H_{{A_{EM} }} & = \frac{{C_{p} }}{{T_{r} }}\overrightarrow {\nabla } \cdot \left( {\left\langle {T_{*} } \right\rangle \left\langle {\overrightarrow {V}^{\prime } T_{*}^{\prime } } \right\rangle } \right) + \frac{{C_{p} }}{{T_{r} }}\frac{{\partial \left( {\left\langle {T_{*} } \right\rangle \left\langle {\omega^{\prime}T_{*}^{\prime } } \right\rangle } \right)}}{\partial p} \\ I_{AB} & = - \frac{{RT_{r} }}{p}\left\langle \omega \right\rangle \\ \end{aligned} $$

where \( l \) is an order unity factor (see “Appendix 7” for details).

The prognostic equation for \( A_{IV} \) is obtained by taking the operation \( \left\langle {\frac{{C_{p} T^{\prime}}}{{T_{r} }}\left( {{\text{Eq}}.\,7 - \left\langle {{\text{Eq}}.\,7} \right\rangle } \right)} \right\rangle \), which gives after some approximations

$$ \frac{{\partial A_{IV} }}{\partial t} = G_{IV} - C_{IV} + C_{A} - F_{{A_{IV} }} - H_{{A_{IV} }} $$
(37)

where

$$ \begin{aligned} A_{IV} & = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T^{\prime 2} } \right\rangle \\ G_{IV} & = l\left\langle {\frac{{T^{\prime}}}{{T_{r} }}Q^{\prime}} \right\rangle \\ C_{IV} & = - \left\langle {\omega^{\prime}\alpha^{\prime}} \right\rangle \\ C_{A} & = - \frac{{\left\langle {\overrightarrow {{V^{\prime}}} T^{\prime}} \right\rangle }}{{T_{r} }} \cdot \overrightarrow {\nabla } \left\langle {C_{p} T} \right\rangle - \frac{{\left\langle {\omega^{\prime}T^{\prime}} \right\rangle }}{{T_{r} }}\frac{{\partial \left\langle {C_{p} T} \right\rangle }}{\partial p} \\ F_{{A_{IV} }} & = \overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle A_{IV} } \right) + \frac{{\partial \left( {\left\langle \omega \right\rangle A_{IV} } \right)}}{\partial p} \\ H_{{A_{IV} }} & = \frac{{C_{p} }}{{2T_{r} }}\left\langle {\overrightarrow {\nabla } \cdot \left( {\overrightarrow {{V^{\prime}}} T^{\prime 2} } \right) + \frac{{\partial \left( {\omega^{\prime}T^{\prime 2} } \right)}}{\partial p}} \right\rangle \\ \end{aligned} $$

where \( l \) is an order unity factor (see “Appendix 8” for details).

There appears to be some analogy between Eq. (37) for local \( A_{IV} \) and that for global APE as established in the seminal work by Lorenz (1955, 1969). By analogy with the work of Pearce (1978) and Marquet (2003a, b) on the concept of APE, \( A_{IV} \) and \( A_{EM} \) can be assimilated to reservoirs attributed to ‘eddy’ and ‘zonal’, namely aE and aZ, respectively. An advantage of the present formulation over Lorenz’ is the absence of a division by \( \partial \bar{\theta }/\partial p \), which is problematic in the neutral planetary boundary layer. A disadvantage is that \( A_{IV} \) contains not only available but also some unavailable potential energy, due to the fact that the basic state temperature \( T_{r} \) does not correspond to the state of minimum potential energy as in Lorenz’ formulation.

4.3 Equations for the pressure-dependent part of available enthalpy

The system of equations is completed by Eq. (33) for \( a_{p} = RT_{r} \ln \left( {\frac{p}{{p_{r} }}} \right) \). Since we are working in pressure coordinates, it follows that \( B = \left\langle {a_{p} } \right\rangle = a_{p} \) and \( a^{\prime}_{p} = 0 \). Then (33) simply becomes

$$ \frac{\partial B}{\partial t} = - F_{B} - I_{AB} $$
(38)

where

$$ \begin{aligned} F_{B} & = \overrightarrow {\nabla } \cdot \left( {B\left\langle {\overrightarrow {V} } \right\rangle } \right) + \frac{{\partial \left( {B\left\langle \omega \right\rangle } \right)}}{\partial p} \\ I_{AB} & = - \frac{{RT_{r} }}{p}\left\langle \omega \right\rangle \\ \end{aligned} $$

5 Ensemble-mean energy cycle

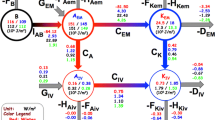
Equations (34)–(38) constitute an approximate set of equations describing the exchanges of ensemble-mean kinetic and available enthalpy energies decomposed into ensemble-mean state variables and deviations thereof, appropriate for the study of an ensemble of simulations performed with a same limited-area model under identical boundary conditions. These equations could easily be integrated over any domain of interest, as long as the lower pressure level does not intersect the topography, resulting in the energy cycle illustrated in Fig. 1. Boxes represent the different energy reservoirs over the domain of interest and arrows indicate energy exchanges between the reservoirs and with regions outside the domain of interest. At this stage, the direction of the arrows is arbitrary and only reflects the choice of sign used in writing the equations.

Fig. 1
figure 1

The energy cycle of the atmosphere as simulated by RCM. The arrows indicate the various fluxes of energy

Full size image

There are 5 reservoirs corresponding to the each of the 5 prognostic equations (34)–(38): \( K_{EM} \) corresponds to the kinetic energy associated with the ensemble-mean wind, \( K_{IV} \) is the kinetic energy associated with the wind deviations from the ensemble mean, \( A_{EM} \) is the temperature-dependent part of available enthalpy associated with the ensemble-mean temperature, \( A_{IV} \) is the temperature-dependent part of available enthalpy associated with the deviations of temperature from the ensemble mean, and \( B \) is the pressure-dependent part of available enthalpy. In global energetics cast in terms of zonal mean and deviations thereof (e.g. Lorenz 1955, 1969; Peixoto and Oort 1992), there would be 4 reservoirs, namely 2 kinetic energy reservoirs and 2 available potential energy reservoirs, each one associated with zonally averaged variables and their deviations. The local energy cycle renders an additional, fifth reservoir \( B \) that reflects the fact that mass is not constant over a limited-area domain, unlike the case when considering the entire globe. By re-examining the formulation of the concept of APE defined by Lorenz, Peace (1978) showed that it is possible to separate the APE into three local energy components (APE = AS + AZ + AE) referred to as static-stability, zonal and eddy reservoirs, respectively, resulting in 5 energy reservoirs for the global circulation. In a similar approach, Marquet (2003a, b) separated the kinetic energy into 3 components (K = KS + KZ + KE), resulting to a cycle of 6 reservoirs in addition of the 3 available enthalpy components established by Pearce. By analogy with the separation made by Pearce (1978) and Marquet (1991), the energy cycle illustrated in Fig. 1 will be modified in the next section in order to reduce the large value of the \( A_{EM} \) energy controlled by the difference between T and Tr.

There are 5 terms that occur, each one, in two of the prognostic equations, but with opposite sign: \( C_{K} \), \( C_{A} \), \( C_{IV} \), \( C_{EM} \) and \( I_{AB} \). These terms represent conversion of energy between reservoirs. \( C_{A} \) represents a conversion of temperature-dependent part of available enthalpy between its \( A_{EM} \) and \( A_{IV} \) forms, and \( C_{K} \) represents a conversion of kinetic energy between its \( K_{EM} \) and \( K_{IV} \) forms. \( C_{EM} \) represents a conversion between the temperature-dependent part of available enthalpy and kinetic energy associated with the ensemble-mean state, \( A_{EM} \) and \( K_{EM} \), respectively; \( C_{IV} \) represents a conversion between the temperature-dependent part of available enthalpy and kinetic energy associated with the deviation from ensemble-mean state, \( A_{IV} \) and \( K_{IV} \), respectively. The fifth term \( I_{AB} \) represents a conversion between the temperature-dependent part of available enthalpy associated with the ensemble-mean state \( A_{EM} \) and the pressure-dependent part of available enthalpy \( B \). Only the first four terms have counterparts in global energetics.

The term \( C_{A} \) represents the effect of covariance of fluctuations (involving \( T^{\prime} \) and \( \overrightarrow {{V^{\prime}}} \)) acting in the direction of the EM temperature gradient. Nikiéma and Laprise (2011b) have shown that, in a CRCM simulation over a North American domain, the horizontal and vertical components of \( C_{A} \) tend to have positive and negative signs, respectively, but the vertical term dominates, so \( C_{A} \) acts as a loss of \( A_{EM} \) in favour of \( A_{IV} \).

The term \( C_{K} \) represents the effect of variance and covariance of wind perturbations in the direction of gradients of the EM horizontal wind. By making a parallel with the energy cycle of weather systems, we will say that this term corresponds to a “barotropic” conversion of kinetic energy between the reservoirs \( K_{EM} \) and \( K_{IV} \).

The terms \( C_{EM} \) and \( C_{IV} \) represent covariances of vertical motion and density, \( - \left\langle \omega \right\rangle \left\langle \alpha \right\rangle \) and \( - \left\langle {\omega^{\prime}\alpha^{\prime}} \right\rangle \), respectively. By making again a parallel with the energy cycle of weather systems, we will say that they correspond to “baroclinic” conversions between reservoirs of kinetic energy and temperature-dependent part of available enthalpy, between \( A_{EM} \) and \( K_{EM} \) for \( C_{EM} \), and between \( A_{IV} \) and \( K_{IV} \) for \( C_{IV} \).

Apart from conversion terms, other terms act as sources or sink of energy in the reservoirs. Terms \( G_{EM} = \frac{l}{{T_{r} }}\;\left\langle {T_{*} } \right\rangle \left\langle Q \right\rangle \, \) and \( G_{IV} = \frac{l}{{T_{r} }}\left\langle {T^{\prime}Q^{\prime}} \right\rangle \) arise due to covariances of diabatic heating and temperature, and they generally act as sources of \( A_{EM} \) and \( A_{IV} \), respectively. Nikiéma and Laprise (2011a, b) found that \( G_{IV} \) exhibits a large intense positive contribution in the troposphere over a North American domain in summer. Terms \( D_{EM} = - \left\langle {\overrightarrow {V} } \right\rangle \cdot \left\langle {\overrightarrow {F} } \right\rangle \) and \( D_{IV} = - \left\langle {\overrightarrow {{V^{\prime}}} \cdot \overrightarrow {{F^{\prime}}} } \right\rangle \) generally act as sinks of kinetic energy \( K_{EM} \) and \( K_{IV} \), respectively, mostly due to surface friction.

The 5 terms \( F_{\psi } \), with \( \psi \,\,\in \,\,\left\{ {K_{EM} ,K_{IV} ,A_{EM} ,A_{IV} ,B} \right\} \), correspond to transport of inter-member variability in \( \psi \). In their study of IV in the potential temperature and vorticity fields, Nikiéma and Laprise (2011b) have shown that the terms \( F_{\psi } \) always contribute negatively as they correspond to export of IV out of the regional domain.

Finally, terms \( H \) represent divergence of covariances involving two or more perturbations from the ensemble mean. These terms would average to zero upon integration over the entire globe, but they must be retained locally or over limited-area domain. Terms \( H_{{K_{IV} }} \) and \( H_{{A_{IV} }} \) are third-order terms, and are usually much smaller than other terms in the budget.

6 Further decomposition in horizontal average on pressure surfaces and deviation thereof

While a clear advantage of the proposed approach in terms of intrinsically defined variable is that the equations possess a local meaning; its main drawback is that \( a_{T} \) cannot readily be associated to some kind of available potential energy as with Lorenz’ APE. This is clearly seen in the vertical profile of \( a_{T} \): from a local minimum at the level where \( T \) is close to \( T_{r} \) on average, its magnitude increases markedly above and below this level as a result of the significant departure of \( T \) from \( T_{r} \), owing to the stratification in the atmosphere. These large departures do not by any means imply de facto some larger reservoir of available potential energy in the upper and lower parts of the atmosphere. There is hence a clear advantage to further splitting \( a_{T} \) into separate components due to mean stratification and deviations thereof, as did Marquet (1991) in his Section 5.

Unlike Marquet (1991), however, here we start from the quadratic approximation to \( a_{T} \):

$$ a_{T} = \frac{{C_{p} }}{{2T_{r} }}\left( {T - T_{r} } \right)^{2} $$
(39)

We introduce \( \overline{T} \), the horizontal average on a pressure surface, such that \( \overline{T}_{m} \left( {p,\,t} \right) \) is a function of member \( m \), pressure \( p \) and time \( t \), and decompose \( a_{T} \) as follows:

$$ \begin{aligned} a_{T} & = \frac{{C_{p} }}{{2T_{r} }}\left\{ {\left( {T - \overline{T} } \right) + \left( {\overline{T} - T_{r} } \right)} \right\}^{2} \\ & = a_{B} + a_{S} + a_{C} \\ \end{aligned} $$
(40)

where

$$ \begin{aligned} a_{B} & = \frac{{C_{p} }}{{2T_{r} }}\left( {T - \overline{T} } \right)^{2} \\ a_{S} & = \frac{{C_{p} }}{{2T_{r} }}\left( {\overline{T} - T_{r} } \right)^{2} \\ a_{C} & = \frac{{C_{p} }}{{2T_{r} }}2\left( {T - \overline{T} } \right)\left( {\overline{T} - T_{r} } \right) \\ \end{aligned} $$

The term \( a_{B} \) is referred to as the baroclinicity component as it depends on deviations from the horizontal averages along isobaric surfaces; the term \( a_{S} \) represents the effect of the mean stratification, and \( a_{C} \) is a cross term involving both effects. The interpretation of the term \( a_{B} \) most closely resembles Lorenz’s APE, while \( a_{S} \) is a much larger term that exhibits a local minimum at the level where \( T \) is close to \( T_{r} \) on average, with marked increases in magnitude above and below this level. It is important to realise however that the individual components \( a_{B} \), \( a_{S} \) and \( a_{C} \) are no more intrinsically defined, as they depend on the extent of the domain considered in carrying the horizontal average.For later use, we introduce the notation

$$ \left( {} \right)^{ \times } = \left( {} \right) - \overline{{\left( {} \right)}} $$
(41)

for deviations from horizontal averages along isobaric surfaces, so that

$$ a_{B} = \frac{{C_{p} }}{{2T_{r} }}\left( {T^{ \times } } \right)^{2} $$
(42)

A noteworthy feature of the components \( a_{B} \), \( a_{S} \) and \( a_{C} \) is that \( \overline{{a_{C} }} = 0 \) and \( \overline{{a_{S} }} = a_{S} \) so that

$$ \begin{aligned} \overline{{a_{T} }} & = \overline{{a_{B} }} + a_{S} \\ & = \frac{{C_{p} }}{{2T_{r} }}\overline{{\left( {T^{ \times } } \right)^{2} }} + \frac{{C_{p} }}{{2T_{r} }}\left( {\overline{T} - T_{r} } \right)^{2} \\ \end{aligned} $$
(43)

It was demonstrated earlier that the ensemble mean of the temperature contribution \( a_{T} \) to potential enthalpy, \( A = \left\langle {a_{T} } \right\rangle \), could be decomposed as \( A = A_{EM} + A_{IV} \) with a component \( A_{EM} = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T - T_{r} } \right\rangle^{2} \) that depends solely on ensemble-mean variables, and a component \( A_{IV} = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T^{\prime 2} } \right\rangle \) that depends on deviations from the ensemble mean. The aforementioned typical vertical structure of \( a_{T} \), with a local minimum at the level where \( T \) is close to \( T_{r} \) on average, and marked increases in magnitude above and below this level, is only present in the term \( A_{EM} \) that depends on ensemble-mean variables. Next we will proceed to further decompose \( A_{EM} \) into contributions from horizontal averages along isobaric surfaces and deviations thereof, and finally we will average these quantities on isobaric surfaces.

The term \( A_{EM} = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T - T_{r} } \right\rangle^{2} \) can be decomposed as

$$ A_{EM} = A_{{EM{\kern 1pt} B}} + A_{{EM{\kern 1pt} S}} + A_{{EM{\kern 1pt} C}} $$
(44)

where

$$ \begin{aligned} A_{{EM{\kern 1pt} B}} & = \frac{{C_{p} }}{{2T_{r} }}\left\langle {T - \overline{T} } \right\rangle^{2} \\ A_{{EM{\kern 1pt} S}} & = \frac{{C_{p} }}{{2T_{r} }}\left\langle {\overline{T} - T_{r} } \right\rangle^{2} \\ A_{{EM{\kern 1pt} C}} & = \frac{{C_{p} }}{{2T_{r} }}2\left\langle {T - \overline{T} } \right\rangle \left\langle {\overline{T} - T_{r} } \right\rangle \\ \end{aligned} $$

After taking the average along isobaric surfaces, the equation becomes

$$ \overline{{A_{EM} }} = \overline{{A_{{EM{\kern 1pt} B}} }} + A_{{EM{\kern 1pt} S}} $$
(45)

where \( \overline{{A_{{EM{\kern 1pt} B}} }} = \frac{{C_{p} }}{{2T_{r} }}\overline{{\left\langle {T - \overline{T} } \right\rangle^{2} }} \) and \( A_{{EM{\kern 1pt} S}} = \frac{{C_{p} }}{{2T_{r} }}\left\langle {\overline{T} - T_{r} } \right\rangle^{2} \) “Appendix 9” gives the algebraic details to establish a prognostic equation for \( \overline{{A_{{EM{\kern 1pt} B}} }} \):

$$ \frac{{\partial \overline{{A_{{EM{\kern 1pt} B}} }} }}{\partial t} = \overline{{G_{{EM{\kern 1pt} B}} }} - \overline{{C_{{EM{\kern 1pt} B}} }} + \overline{{C_{{EM{\kern 1pt} BS}} }} - \overline{{C_{{A{\kern 1pt} B}} }} - \overline{{F_{{A_{EM} {\kern 1pt} B}} }} - \overline{{H_{{A_{EM} {\kern 1pt} B}} }} $$
(46)

where

$$ \begin{aligned} \overline{{A_{{EM{\kern 1pt} B}} }} & = \frac{{C_{p} }}{{2T_{r} }}\overline{{\left\langle {T^{ \times } } \right\rangle^{2} }} \quad {\text{and}}\quad T^{ \times } = T - \overline{T} \\ \overline{{G_{{EM{\kern 1pt} B}} }} & = \frac{l}{{T_{r} }}\left\langle {T_{*} } \right\rangle \left\langle Q \right\rangle { = }\overline{{\left\langle {T^{ \times } } \right\rangle \left\langle \frac{Q}{T} \right\rangle }} = \overline{{\left\langle {T^{ \times } } \right\rangle \left\langle {\left( \frac{Q}{T} \right)^{ \times } } \right\rangle }} \approx \frac{l}{{T_{r} }}\overline{{\left\langle {T^{ \times } } \right\rangle \left\langle {Q^{ \times } } \right\rangle }} \\ \overline{{C_{{EM{\kern 1pt} B}} }} & = - \overline{{\left\langle {\omega^{ \times } } \right\rangle \left\langle {\alpha^{ \times } } \right\rangle }} \\ \overline{{C_{{EM{\kern 1pt} BS}} }} & = - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\frac{{\partial \overline{T} }}{\partial p}\omega^{ \times } } \right\rangle \left\langle {T^{ \times } } \right\rangle }} \\ \overline{{C_{AB} }} & = - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\overrightarrow {V}^{\prime } T^{ \times \prime } } \right\rangle \cdot \overrightarrow {\nabla } \left\langle {T^{ \times } } \right\rangle }} - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\omega^{\prime}T^{ \times \prime } } \right\rangle \frac{\partial }{\partial p}\left\langle {T^{ \times } } \right\rangle }} \\ & = - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\overrightarrow {V}^{\prime } T^{ \times \prime } } \right\rangle \cdot \overrightarrow {\nabla } \left\langle T \right\rangle }} - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\omega^{\prime}T^{ \times \prime } } \right\rangle \frac{\partial }{\partial p}\left\langle {T^{ \times } } \right\rangle }} \\ \overline{{F_{{A_{EM} {\kern 1pt} B}} }} & = \overline{{\overrightarrow {\nabla } \cdot \left( {A_{{EM{\kern 1pt} B}} \left\langle {\overrightarrow {V} } \right\rangle } \right)}} + \frac{\partial }{\partial p}\overline{{\left( {A_{{EM{\kern 1pt} B}} \left\langle \omega \right\rangle } \right)}} \\ \overline{{H_{{A_{EM} {\kern 1pt} B}} }} & = \frac{{C_{p} }}{{T_{r} }}\overline{{\overrightarrow {\nabla } \cdot \left( {\left\langle {T^{ \times } } \right\rangle \left\langle {\overrightarrow {V}^{\prime } T^{ \times \prime } } \right\rangle } \right)}} + \frac{{C_{p} }}{{T_{r} }}\frac{\partial }{\partial p}\overline{{\left( {\left\langle {T^{ \times } } \right\rangle \left\langle {\omega^{\prime}T^{ \times \prime } } \right\rangle } \right)}} \\ \end{aligned} $$

Using the relation \( A_{{EM{\kern 1pt} S}} = \overline{{A_{EM} }} - \overline{{A_{{EM{\kern 1pt} B}} }} \), a prognostic equation for \( A_{{EM{\kern 1pt} S}} = \frac{{C_{p} }}{{2T_{r} }}\left\langle {\overline{T} - T_{r} } \right\rangle^{2} \) can be obtained by subtracting the equation just obtained for \( \overline{{A_{{EM{\kern 1pt} B}} }} = \frac{{C_{p} }}{{2T_{r} }}\overline{{\left\langle {T - \overline{T} } \right\rangle^{2} }} \) from that for \( \overline{{A_{EM} }} = \frac{{C_{p} }}{{2T_{r} }}\overline{{\left\langle {T - T_{r} } \right\rangle^{2} }} \) (details are provided in “Appendix 10”)

$$ \frac{\partial }{\partial t}\overline{{A_{{EM{\kern 1pt} S}} }} = \overline{{G_{{EM{\kern 1pt} BS}} }} - \overline{{C_{{EM{\kern 1pt} S}} }} - \overline{{C_{{EM{\kern 1pt} BS}} }} - \overline{{C_{{A{\kern 1pt} S}} }} - \overline{{F_{{A_{EM} {\kern 1pt} S}} }} - \overline{{H_{{A_{EM} {\kern 1pt} S}} }} $$
(47)

where

$$ \begin{aligned} \overline{{G_{{EM{\kern 1pt} S}} }} & = \frac{l}{{T_{r} }}\left\{ {\left( {\left\langle {\overline{T} } \right\rangle - T_{r} } \right)\overline{\left\langle Q \right\rangle } } \right\} \\ \overline{{C_{{EM{\kern 1pt} S}} }} & = \overline{{C_{EM} }} - \overline{{C_{{EM{\kern 1pt} B}} }} - \overline{{I_{AB} }} = - \left\langle {\overline{\omega } } \right\rangle \left( {\left\langle {\overline{\alpha } } \right\rangle - \alpha_{r} } \right) \\ \overline{{C_{{EM{\kern 1pt} BS}} }} & = - \frac{{C_{p} }}{{T_{r} }}\overline{{\left\langle {\frac{{\partial \overline{T} }}{\partial p}\omega^{ \times } } \right\rangle \left\langle {T^{ \times } } \right\rangle }} \\ \overline{{C_{{A{\kern 1pt} S}} }} & = - \frac{{C_{p} }}{{T_{r} }}\left\{ {\overline{{\left\langle {\overrightarrow {V}^{\prime } \overline{{T^{\prime}}} } \right\rangle \cdot \overrightarrow {\nabla } \left\langle T \right\rangle }} } \right\} - \frac{{C_{p} }}{{T_{r} }}\left\{ {\overline{{\left\langle {\omega^{\prime}T^{\prime}} \right\rangle }} \frac{\partial \;}{\partial p}\left\langle {\overline{T} } \right\rangle + \overline{{\left\langle {\omega^{\prime}\overline{{T^{\prime}}} } \right\rangle \frac{\partial }{\partial p}\left\langle {T^{ \times } } \right\rangle }} } \right\} \\ \overline{{F_{{A_{EM} {\kern 1pt} S}} }} & = \overline{{\overrightarrow {\nabla } \cdot \left( {\left\langle {\overrightarrow {V} } \right\rangle A_{{EM{\kern 1pt} S}} } \right)}} + \;\frac{\partial }{\partial p}\overline{{\left\langle \omega \right\rangle A_{{EM{\kern 1pt} S}} }} \\ \overline{{H_{{A_{EM} {\kern 1pt} S}} }} & = \frac{{C_{p} }}{{T_{r} }}\left\{ {\overline{{\overrightarrow {\nabla } \cdot \left( {\overline{{\left\langle {T_{*} } \right\rangle }} \left\langle {\overrightarrow {V}^{\prime } T^{\prime } } \right\rangle } \right) + \left( {\left\langle {T^{ \times } } \right\rangle \left\langle {\overrightarrow {V}^{\prime } \overline{{T^{\prime}}} } \right\rangle } \right)}} } \right\} \\ & \quad + \frac{{C_{p} }}{{T_{r} }}\frac{\partial }{\partial p}\left\{ {\overline{{\left\langle {T_{*} } \right\rangle }} \overline{{\left\langle {\omega^{\prime}T^{\prime } } \right\rangle }} + \overline{{\left\langle {T^{ \times } } \right\rangle \left\langle {\omega^{\prime}\overline{{T^{\prime}}} } \right\rangle }} } \right\} \\ \end{aligned} $$

“Appendix 11” summarizes the isobaric energy cycle equations.

Figure 2 illustrates and summarizes the energy cycle obtained by considering the average on pressure surfaces and deviation thereof. As a consequence, there are 6 reservoirs corresponding to four prognostic equations of AIV, KIV, KEM and B defined over the isobaric surfaces (see “Appendix 11”) and two equations resulting to the decomposition of \( \overline{{A_{EM} }} \) into two contributions: \( A_{EM\,S} \) and \( \overline{{A_{EM\,B} }} \) referred to the stratification and the baroclinic components, respectively. The further decomposition along the isobaric surfaces leads to new conversion terms: \( \overline{{C_{EM\,BS} }} \), \( \overline{{C_{AS} }} \), \( \overline{{C_{AB} }} \), \( \overline{{C_{EM\,B} }} \) and \( \overline{{C_{EM\,S} }} \). The first one represents the conversion term between the two new reservoirs (AEM S and AEM B), whereas the other ones are contributions of two main conversion terms, namely \( \overline{{C_{EM} }} \) (=\(\overline{{C_{EM \, B} }} + \overline{{C_{{EM{\text{ S}}}} }} + \overline{{I_{AB} }} \)) and \( \overline{{C_{A} }} \) (=\(\overline{{C_{AB} }} + \overline{{C_{{A{\text{S}}}} }} \)). This decomposition is advantageous because the large values of \( \overline{{C_{EM} }} \) are now separated in several components.

Fig. 2
figure 2

Regional energy cycle averaged on pressure surface

Full size image

7 Conclusions

The motivation of this paper was to establish a formalism that would allow studying the energetics associated with the time fluctuations of inter-member spread (or internal variability, IV) in an ensemble of simulations of a nested, limited-area model driven by a given set of lateral boundary conditions, when only the timing to start each run differs amongst the members of the ensemble. This framework implies that IV develops internally to the RCM domain. The lateral sponge zone along the perimeter of the regional domain constitute a transition zone between the imposed lateral boundary condition and the free internal domain. In the sponge zone the RCM internal solution is forced towards the same driving data for all members, and hence IV is suppressed there. The regional domain where the diagnostic equations would be applied should therefore exclude the sponge zone.

The challenge was to write a set of consistent energy equations that could be used locally or over a limited-area domain, unlike classical energetics studies of weather systems following the seminal work of Lorenz (1955, 1967) that are only meaningful globally (van Mieghem 1972). Following the work of Nikiéma and Laprise (2011b) on inter-member variance, and by analogy with the frameworks of Pearce (1978) and Marquet (1991) for atmospheric energetics, prognostic equations for ensemble-mean kinetic energy and available enthalpy were approximated and decomposed into contributions due to ensemble-mean variables (EM) and due to deviations from the ensemble mean (IV). This led to a set of approximate equations corresponding to an energy cycle for inter-member variability in ensemble simulations of a nested model. These equations were then averaged on pressure surfaces. Interestingly enough, several terms in the energy cycle for IV have a form similar to that of the energetics studies of weather systems (Lorenz 1955; Pearce 1978; Marquet 1991, 2003a, b), including for example baroclinic and barotropic conversions, diabatic generation of available enthalpy and friction dissipation of kinetic energy. This study purposely used a quadratic expression of the available enthalpy because it offers the great advantage of separating the contribution of \( \left\langle {a_{T} } \right\rangle \) into \( A_{EM} \) and \( A_{IV} \) that are proportional to \( \left\langle T \right\rangle^{2} \) and \( \left\langle {T^{\prime 2} } \right\rangle \), respectively, thus allowing an immediate physical interpretation and retaining the conventional definition of IV (i.e. \( \sigma_{IV} \approx \left\langle {T^{\prime 2} } \right\rangle \)) in regional climate modelling studies.

While most models are cast in terrain-following coordinate to facilitate the implementation of the kinematic lower boundary condition, we chose to formulate our diagnostic equations in pressure coordinates, following a long tradition in diagnostic studies, whose advantages have been argued for example by Boer (1982). Amongst the reasons is that this choice avoids the presence of several metric terms that appear in terrain-following coordinates, which do not have an immediate physical interpretation. When lateral averaging is applied, such averaging along terrain-following coordinate would not lead to an easy interpretation. Finally, we would want eventually to scale-decompose the terms in the budget equations, and such decomposition would be inappropriate in anything but roughly horizontal surfaces. As mentioned briefly in relation to (20), the field equations are only valid above ground, i.e. on pressure levels satisfying the condition \( p\,\le\,p_{Min} \), where \( p_{Min} \) is the minimum value of surface pressure encountered in the time and space domain under study. Levels intersecting topography could in principle be treated using the masking procedure of Boer (1982); we will not pursue this avenue here however.

In a forthcoming work (Nikiéma and Laprise, in preparation), the contribution of each term in the energy cycle for IV will be evaluated for an ensemble of 50 simulations performed over an annual cycle with version 5 of the Canadian RCM (CRCM5). Previous work (Nikiéma and Laprise 2011a, b) lend us confidence to obtain a quantitatively acceptable accuracy despite the numerous approximations involved in evaluating each term, such as interpolations from model coordinates to pressure levels, interpolating variables from their Arakawa C-grid staggering in the model, calculating transport in Eulerian flux form rather than with the semi-Lagrangian scheme as in the model, and using only samples of time steps that are archived, to name but a few.