Examination of the global lorenz energy cycle using MERRA and NCEP-reanalysis 2

Abstract

In this study, the global Lorenz atmospheric energy cycle is evaluated using the Modern Era Retrospective analysis for Research and Applications (MERRA) and the National Center for Environmental Prediction and the Department of Energy (NCEP R2) reanalysis datasets over a 30-year period (1979–2008) for the annual, JJA, and DJF means. The energy cycle calculated from the two reanalysis datasets is largely consistent, but the energy cycle determined using the MERRA dataset is more active than that determined from the NCEP R2 dataset. For instance, with regard to the annual mean, the general discrepancy between the energy components in the global integral is about 5 %, whereas the discrepancy between the conversion components is about 16  %, with the exception of C(P_M, K_M), which has a different sign in the global integrals. The latitude-altitude cross-section indicates that the difference in the energy cycle of the two reanalysis datasets is larger in the southern hemisphere than in the northern hemisphere. The conversion rates of mean available potential energy to mean kinetic energy [C(P_M, K_M)] and eddy available potential energy to eddy kinetic energy [C(P_E, K_E)] are also calculated using two formulations (so-called ‘v·grad z’ and ‘ω·α’) for the two reanalysis datasets. The differences in the conversion rate between the two reanalysis datasets for the global integral are not appreciable for the two formulations.

1 Introduction

Lorenz (1955) proposed the energy cycle as a mechanism to enable easy understanding of atmospheric circulation from the perspective of energy conversion by considering the physical processes involved, from the generation of potential energy by solar energy to the dissipation of kinetic energy. To construct an energy cycle, the mean available potential energy (P_M) is generated by net radiation heating from the incoming solar radiation and the release of latent heat in the tropics, as well as by net infrared cooling in the polar region. P_M is converted into eddy-available potential energy (P_E) by the growing baroclinic disturbances, and then P_E is converted into eddy kinetic energy (K_E) based on the baroclinic instability, which is induced by the sinking of colder air and the rising of warmer air by the eddies. Some portion of K_E is converted into the mean kinetic energy (K_M) of the mean flow in a barotropic process. However the bulk of the kinetic energy of large-scale eddies is dissipated by surface friction and turbulence. In the tropics, the direct circulation (Hadley cell) generates a zonal angular momentum in the upper branch of the circulation, which is related to the generation of K_M. Therefore, P_M is converted into K_M [C(P_M, K_M) > 0]. The indirect circulation (Ferrel cell) in the midlatitude, however, consumes K_M at a slightly faster rate than K_M is produced in the Hadley cell, and thus converts some of the K_M back into P_M [C(P_M, K_M) < 0]. The energy conversion follows the path P_M → P_E → K_E → K_M (Peixoto and Oort 1992).

Because formulations of the energy cycle involve climate statistics, which are the deviations of time, zonal means, and variance and covariance of basic variables, it is very useful to either diagnose climate models (Sheng and Hayashi 1990; Boer and Lambert 2008; Hernández-Deckers and von Storch 2010; Marques et al. 2011) or analyze the characteristics of various reanalysis datasets (Ulbrich and Speth 1991; Hu et al. 2004; Li et al. 2007; Marques et al. 2009; Marques et al. 2010). Recently, various reanalysis datasets such as the NCEP R2, ERA-40 from the European Center for Medium-range Weather Forecasts (ECMWF), and JRA-25 from the Japan Meteorological Agency (JMA) and the Central Research Institute of Electric Power Industry (CRIEPI), have been released to satisfy the demand for atmosphere datasets; many researchers have since used such reanalysis datasets to investigate the atmosphere energy cycle. Li et al. (2007) and Marques et al. (2009) examined the global atmospheric energy cycle based on monthly evaluations using two reanalysis datasets (NCEP R2 and ERA-40) covering the 23 years from 1979 to 2001. Li et al. (2007) determined that the conversion rate C(P_M, K_M) had changed in that its sign differed from that reported in a previous study (Oort 1983), which suggests that near-surface processes play an important role in the magnitude and sign of C(P_M, K_M). Marques et al. (2010) compared three reanalysis datasets (NCEP R2, ERA-40, and JRA-25) using global energy analysis for all seasons. They found that the Lorenz energy cycles of the three datasets were similar, but that appreciable differences appeared mainly in the southern hemisphere and that the magnitudes of the energy and conversion terms tended to follow the hierarchy of ERA-40 > JRA-25 > NCEP-R2. Boer and Lambert (2008) compared the simulation performance of 12 models in the second Atmospheric Model Intercomparison Project (AMIP 2) with regard to the energy cycle, and compared the generated energy cycles with the energy cycles obtained based on the NCEP R2 and ERA 40 datasets. Previous studies showed that the models generally simulated a modestly overactive energy cycle, i.e., one where there is excessive generation of P_M and excessive dissipation of K_E.

In this study, we evaluate the Lorenz atmospheric energy cycle using a new reanalysis dataset, MERRA (Rienecker et al. 2011), from the point of view of the global integral and latitude-altitude cross-sections of the global energy components (P_M, P_TE, P_SE, K_M, K_TE, and K_SE) and conversion components [C(P_M, P_TE), C(P_M, P_SE), C(P_TE, K_TE), C(P_SE, K_SE), C(K_TE, K_M), C(K_SE, K_M), C(P_SE, P_TE), C(K_SE, K_TE), and C(P_M, K_M)]. We also investigate the Lorenz energy cycle from a climatology perspective based on the two reanalysis datasets to fully characterize the energy cycle in MERRA and compare it with that in NCEP R2.

2 Data and methodology

In this study, two reanalysis datasets from NCEP R2 and MERRA are used to compute the Lorenz energy cycle over a 30-year period (1979–2008). MERRA was produced using the Goddard Earth Observing System Data Assimilation System Version 5 (GEOS-5), which consists of the GEOS-5 atmospheric model and the Grid-point Statistical Interpolation (GSI) analysis system [jointly developed by the Global Modeling and Assimilation Office (GMAO) and NOAA’s National Center for Environmental Prediction]. The GEOS-5 assimilation system includes an incremental analysis update (IAU) procedure (Bloom et al. 1996) that slowly adjusts the model states towards the observed state. This process has the advantage of minimizing any unrealistic spin-down (or spin-up) of the water cycle. We use the standard daily output that is provided for 42 pressure levels with a horizontal resolution of 1.25° latitude × 1.25° longitude and a temporal resolution of eight times per day from 1979 to 2008. The spatial resolution of NCEP R2 is 2.5° latitude × 2.5° longitude with 17 pressure levels, and its temporal resolution is four times per day. In contrast, the MERRA dataset has 42 levels of vertical resolution; however, to calculate the energy cycle, we use only 17 vertical levels so as to match the resolution of the NCEP R2 dataset.

We computed the energy cycle for the entire globe by applying the equations developed by Peixoto and Oort (1974), although we excluded the level below ground to calculate the terms of the energy cycle equations using topography. Energy cycle equations consist of energy terms, conversion rate terms, and generation and dissipation terms, as illustrated in Eqs. (7)–(16). The symbols, definitions, and equations used in this study are described in the “Appendix”. Energy generation and dissipation are calculated from the residual values using Eqs. (1)–(6). The energy cycle is computed in horizontal integrals over the entire globe and in vertical integrals from 1,000 to 10 hPa.

$$ \frac{{\partial {\text{P}}_{\text{M}} }}{\partial t} = {\text{G}}({\text{P}}_{\text{M}} ) - {\text{C}}({\text{P}}_{\text{M}} , {\text{ P}}_{\text{E}} ) - {\text{C}}({\text{P}}_{\text{M}} , {\text{ K}}_{\text{M}} ) $$

(1)

$$ \frac{{\partial {\text{P}}_{\text{TE}} }}{\partial t} = {\text{G}}({\text{P}}_{\text{TE}} ) + {\text{C}}({\text{P}}_{\text{M}} , {\text{ P}}_{\text{TE}} ) - {\text{C}}({\text{P}}_{\text{TE}} , {\text{ K}}_{\text{TE}} ) + {\text{C}}({\text{P}}_{\text{SE}} , {\text{ P}}_{\text{TE}} ) $$

(2)

$$ \frac{{\partial {\text{P}}_{\text{SE}} }}{\partial t} = {\text{G}}({\text{P}}_{\text{SE}} ) + {\text{C}}({\text{P}}_{\text{M}} , {\text{ P}}_{\text{SE}} ) - {\text{C}}({\text{P}}_{\text{SE}} , {\text{ K}}_{\text{SE}} ) - {\text{C}}({\text{P}}_{\text{SE}} , {\text{ P}}_{\text{TE}} ) $$

(3)

$$ \frac{{\partial {\text{K}}_{\text{M}} }}{\partial t} = - {\text{D}}({\text{K}}_{\text{M}} ) + {\text{C}}({\text{P}}_{\text{M}} , {\text{K}}_{\text{M}} ) + {\text{C}}({\text{K}}_{\text{E}} , {\text{K}}_{\text{M}} ) $$

(4)

$$ \frac{{\partial {\text{K}}_{\text{TE}} }}{\partial t} = - {\text{D}}({\text{K}}_{\text{TE}} ) + {\text{C}}({\text{P}}_{\text{TE}} , {\text{ K}}_{\text{TE}} ) - {\text{C}}({\text{K}}_{\text{TE}} , {\text{ K}}_{\text{M}} ) + {\text{C}}({\text{K}}_{\text{SE}} , {\text{ K}}_{\text{TE}} ) $$

(5)

$$ \frac{{\partial {\text{K}}_{\text{SE}} }}{\partial t} = - {\text{D}}({\text{K}}_{\text{SE}} ) + {\text{C}}({\text{P}}_{\text{SE}} , {\text{ K}}_{\text{SE}} ) - {\text{C}}({\text{K}}_{\text{SE}} , {\text{ K}}_{\text{M}} ) - {\text{C}}({\text{K}}_{\text{SE}} , {\text{ K}}_{\text{TE}} ) $$

(6)

The eddy energy is decomposed into transient and stationary eddy available potential/kinetic energy. The subscript “M” represents the zonal mean component; “TE”, the transient eddy component; and “SE”, the stationary eddy component. These indicate that the eddy component comprises transient eddies and stationary eddies: P_E(K_E) = P_TE (K_TE) + P_SE (K_SE).

The conversion rates of available potential energy to kinetic energy [C(P_M, K_M) and (P_E, K_E)] can be written as two possible formulations: the so-called ‘v·grad z’ formulation and the ‘ω·α’ formulation (12 and 14). The ‘v·grad z’ formation comes from the equations of motion and the ‘ω·α’ formation is obtained from the thermodynamic equation. The physical process invoked in the two formulations is different. For instance, the conversion rate, C(P_M, K_M), that is computed with the first formulation indicates a horizontal cross-isobaric flow down the north–south pressure gradient, while that which is computed with the second formulation refers to the rising of relatively warm air and the sinking of relatively cold air in the mean meridional circulation, as reflected in the Hadley and Ferrel cells (Marques et al. 2009). Provided that the global integrals are considered, the two formulations are equivalent (Peixoto and Oort 1992). We conducted a sensitivity test for the two formulations using two reanalysis datasets to confirm the consistency of the results. The time average is the monthly time scale based on the daily data, and the transient eddy departs from the monthly average, because most cyclone and anti-cyclone activities have time scales of less than 1 month. We examine the annual, June–July–August (JJA), and December–January–February (DJF) means of the energy cycles.

3 Results

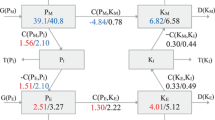
The energy cycles of the 30-year annual mean states of the global integrals of the NCEP R2 and MERRA datasets are shown in Fig. 1. The two values that surround each symbol indicate NCEP R2 (top) and MERRA (bottom), respectively. The terms C(P_M, K_M) and C(P_E, K_E) that are computed with the ‘ω·α’ formulation are shown in parentheses. To confirm the seasonal variation of the energy cycle, the JJA and DJF means were calculated, and are shown in Figs. 2 and 3.

Fig. 1

The lorenz energy cycle diagram from the NCEP R2 (above) and MERRA (below) reanalysis datasets, averaged over the period 1979–2008 (30 years). The values in parentheses were obtained using the ‘ω·α’ formulation. Units are 10⁵ Jm⁻² for energy and Wm⁻² for the conversion rate, generation, and dissipation terms. The arrows indicate the direction that corresponds to positive values. Negative values imply the opposite direction

Fig. 2

The same as Fig. 1, except for the JJA mean

Fig. 3

The same as Fig. 1, except for the DJF mean

The atmospheric energy cycle calculations based on the global integral of the NCEP R2 dataset (values from the MERRA dataset are included in parentheses for comparison) can be summarized as follows. Net heating at low latitudes and net cooling at high latitudes results in a G(P_M) of 1.68 (1.72) Wm⁻². P_M is converted into P_E at a rate of 1.63 (1.78) Wm⁻². P_E is generated at a rate of 0.19 (0.27) Wm⁻² by surpassing latent heating. P_E is converted into K_E at a rate of 1.82 (2.05) Wm⁻². A large part of this energy is dissipated by both friction and turbulence at a rate of 1.41 (1.61) Wm⁻², and the remainder is converted into K_M at a rate of 0.41 (0.44) Wm⁻². K_M is then dissipated by friction at a rate of 0.45 (0.38) Wm⁻². Finally, the P_M is converted into K_M by the zonal mean meridional overturnings, which are the combined actions of the Hadley and Ferrel cells at a rate of 0.04 (−0.06) Wm⁻² (see Fig. 1).

Overall, the global energy cycles from the two reanalysis datasets are similar, but the calculated energy components of the MERRA dataset are about 5 % larger, on average, than those of the NCEP R2 dataset for the annual mean. With regard to the JJA and DJF means, the energy components of the MERRA dataset are larger than those of NCEP R2 by about 6 and 4 % on average, respectively. In particular, the transient eddy energy terms of MERRA (P_TE and K_TE) are about 10 % larger than those of NCEP R2. The magnitude of the conversion rate of MERRA is larger than that of NCEP R2, but the direction of the energy flow is consistent between the two datasets except for C(P_M, K_M). Although the percentage difference of C(P_M, K_M) is larger than that of the other components, the difference is negligible because of the small magnitude of the term.

Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 show the structures of the latitude-altitude cross-sections of the atmospheric energy cycle. In Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, positive shading values indicate that the energy quantities of the MERRA data are larger than those of the NCEP R2 data.

Fig. 4

Latitude-altitude cross-sections of the zonal mean available potential energy, P_M, averaged over 1979–2008 for the annual mean (top), JJA mean (middle), and DJF mean (bottom) for the NCEP R2 (left) and MERRA (right) reanalysis datasets. The contours and shading indicate the energy quantity P_M and the difference between MERRA and NCEP R2, respectively. The contour interval is 30 up to 150, 50 up to 200, and 100 afterwards. Units are 10⁵ J/m²/hPa

Fig. 5

The same as Fig. 4, except for the eddy available potential energy, P_E. The contour interval is 3

Fig. 6

The same as Fig. 4, except for the mean kinetic energy, K_M. The contour interval is 10

Fig. 7

The same as Fig. 4, except for the eddy kinetic energy, K_E. The contour interval is 5

Fig. 8

The same as Fig. 4, except for the conversion rate of the zonal mean potential energy to the eddy potential energy, C(P_M, P_E). The contour interval is 1 up to 0 and is 2 afterwards. Units are W/m²/hPa

Fig. 9

The same as Fig. 4, except for the conversion rate of the eddy potential energy to the eddy kinetic energy, C(P_E, K_E) (with the ‘v·grad z’ formulation). The contour interval is 1 up to 0 and is 4 afterwards. Units are W/m²/hPa

Fig. 10

The same as Fig. 4, except for the conversion rate of the eddy potential energy to the eddy kinetic energy, C(P_E, K_E) (with the ‘ω·α’ formulation). The contour interval is 1 up to 0 and is 2 afterwards. Units are W/m²/hPa

Fig. 11

The same as Fig. 4, except for the conversion rate of the eddy kinetic energy to the zonal mean kinetic energy, C(K_E, K_M). The contour interval is 1. Units are W/m²/hPa

Fig. 12

The same as Fig. 4, except for the conversion rate of the zonal mean potential energy to the zonal mean kinetic energy, C(P_M, K_M) (with the ‘v·grad z’ formulation). The contour interval is 4. Units are W/m²/hPa

Fig. 13

The same as Fig. 4, except for the conversion rate of the zonal mean potential energy to the zonal mean kinetic energy, C(P_M, K_M) (with the ‘ω·α’ formulation). The contour interval is 4. Units are W/m²/hPa

Figure 4 shows the latitude-altitude cross-section of the zonal available potential energy, P_M. The general patterns of the two reanalysis datasets are similar in that the maxima of P_M are displayed around high latitudes, indicating that the largest temperature perturbations from the global average are found at high latitudes. Moreover, the contribution to P_M is greater in the southern hemisphere than in the northern hemisphere, because the temperatures are lower over the Antarctic continent than over the Arctic Ocean, which leads to a larger meridional temperature gradient in the southern hemisphere. The P_M from NCEP R2 is larger at low and middle levels (1,000–500 hPa in the southern hemisphere and 1,000–700 hPa in the northern hemisphere) in both hemispheres, but the P_M from MERRA is larger in the upper level (400–200 hPa) over the high-latitude 60–90°S/N) with regard to the annual mean. Even during the winter season in the northern hemisphere, there is still a significant difference between MERRA and NCEP R2. The cross-sections of the eddy available potential energy, P_E, shown in Fig. 5, are analogous to the structure of P_M, except for the location of the maxima P_E, which is slightly displaced toward the equator. The maximum of P_E is located near the surface at over 60°N in both reanalysis datasets, where the low-level maximum is associated with the structure of growing extratropical cyclones. Note that P_E has a large seasonal variation, especially over high latitudes at near-surface level in both hemispheres (Fig. 5c, f). Overall, the patterns of P_E are similar, but the P_E from MERRA is larger than that from NCEP R2, especially at the upper levels (600–200 hPa) and the stratosphere in the southern hemisphere, and is smaller at the near-surface level (1,000–800 hPa) in the northern hemisphere. The difference in the global integrals of P_E between MERRA and NCEP R2 is 9 % for JJA and 5 % for DJF.

Figure 6 shows that the K_M patterns are related to the jet stream in the troposphere and stratosphere. The maxima regions of K_M are located at 30°S and 30°N over 200 hPa in both reanalysis datasets. The K_M patterns of the two datasets are similar in the northern hemisphere. In the southern hemisphere, the K_M of MERRA is larger than that of NCEP R2 at 30°S and 60°S in the upper-level atmosphere. The maximum regions of K_M in MERRA are widely spread out in the stratosphere, which is a response to the movement and location of the jet stream. These values indicate that the wind variation over the jet streams in the troposphere and stratosphere in MERRA is highly overestimated compared to that in NCEP R2. The K_E patterns are related to the K_M patterns, but the maximum K_E is slightly displaced toward the poles (Fig. 7). The patterns of the cross-section of K_E in MERRA and NCEP R2 are similar, but the K_E in MERRA is larger than in NCEP R2 near the southern hemisphere jet stream in the troposphere and stratosphere. The discrepancy in the global integrals of K_E is about 6 %.

Figure 8 shows the structure of the conversion rate, C(P_M, P_E), in the vertical cross-section. In both hemispheres and for both datasets, the positive maxima of the conversion rate, C(P_M, P_E), are located at the middle latitudes (30–60°) in the middle troposphere, and the negative values are found in the upper troposphere and the low stratosphere. The conversion term, C(P_M, P_E), from MERRA is larger at the mid-level in the southern hemisphere than that from NCEP R2 in the JJA season, and is smaller at the near-surface level in the northern hemisphere than that from NCEP R2 in the DJF season. Note that C(P_M, P_E) is associated with growing baroclinic disturbances–that is, to reduce the meridional difference in the temperatures, this conversion rate added additional variance in the east–west direction. The largest difference in the global integrated values of the conversion term is between MERRA and NCEP R2 in the JJA season (12 %). In Fig. 9, the maxima of the conversion rate, C(P_E, K_E), which are computed with the ‘v·grad z’ formulation, are observed near the surface around the South Pole. They are related to heat-driven rising and sinking motions over Antarctica (Li et al. 2007). In the South Pole, the maximum C(P_E, K_E) from the MERRA dataset is larger than that from NCEP R2 in the lower-level atmosphere. However, the conversion term from MERRA is small in the DJF season near the surface over the northern hemisphere, related to the mid-latitude anticyclone/cyclone activity. These facts contribute to the observed differences in the global integrals of the two reanalysis datasets: 11 % for the annual mean, 15 % for the JJA mean, and 8 % for the DJF mean. Figure 10 shows the conversion rate, C(P_E, K_E), computed with the ‘ω·α’ formulation. The positive signs of the conversion rate are located at the upper levels (400–700 hPa) of the mid-latitude and near-surface levels of the polar region in the southern hemisphere, and the negative signs come from the mid-latitude, above 200 hPa. The C(P_E, K_E) quantities in MERRA are larger than those in NCEP R2 at the upper levels, and are lower at the near-surface level over the polar region in the southern hemisphere. The difference between the global integrals based on the MERRA and NCEP R2 datasets reach 9 % for the annual mean, 11 % for the JJA mean, and 6 % for the DJF mean. The difference between the two reanalysis datasets for the conversion rate computed with the ‘v·grad z’ formulation is larger than computed with the ‘ω·α’ formulation, and the difference between the two formulations is greater in MERRA than in NCEP R2. The first formulation of C(P_E, K_E) contributes to the low-level troposphere; conversely, the second formulation subscribes to the mid-level atmosphere. Both positive and negative values were seen for C(K_E, K_M), which measures barotropic processes, over the jet stream regions in the troposphere and stratosphere in both datasets (Fig. 11). Likewise, C(K_E, K_M) indicates increased zonal motion as a result of the poleward transport of momentum by the motion of eddies. The conversion rate calculated from the MERRA dataset is larger than that calculated from the NCEP R2 dataset at the centers of 20 and 70°S over the upper troposphere in the southern hemisphere, and is smaller over the center of 35°S and near the surface in the southern hemisphere. These features are found largely in the JJA season. Figure 12 shows the cross-section for the conversion rate, C(P_M, K_M), computed using the ‘v·grad z’ formulation. Comparison of the two datasets shows that the positive centers of C(P_M, K_M) from MERRA, which correspond to the Hadley cell in the troposphere of both hemispheres (20° and 200 hPa), are smaller than the corresponding positive centers from NCEP R2. The negative centers of C(P_M, K_M) from MERRA, which correspond to the Ferrel cell in the troposphere (50° and 200 hPa) and to the jet stream in the stratosphere of both hemispheres, are much smaller than those from NCEP R2. In Fig. 13, the cross-sections for the conversion rate, C(P_M, K_M), computed with the ‘ω·α’ formulation, show a positive sign in the equator and both polar regions, and a negative sign centered around 20° and 60°. Positive signs are also found in the upper troposphere and lower stratosphere. These features are similar in the two reanalysis datasets, but a quantitative difference is observed in the tropical region and at a low level in the southern hemisphere. The C(P_M, K_M) computed with both the ‘v·grad z’ and ‘ω·α’ formulations has the same direction in the global integrals. In the cross-section, however, the difference between MERRA and NCEP R2 is marked when the second formulation is used, in contrast to the first formulation.

4 Conclusions

In this study, the MERRA dataset, which is the latest reanalysis dataset from NASA GMAO, was evaluated from the global atmosphere perspective of the Lorenz energy cycle and was compared with the NCEP R2 reanalysis dataset through a global energetics analysis using annual, JJA, and DJF means.

Comparison of the global atmospheric energy cycles of the MERRA and NCEP R2 datasets revealed that the energy cycle calculated using these two datasets was largely consistent, but the magnitude of the energy cycle in the MERRA dataset was generally larger than that of the NCEP R2 dataset. The discrepancy between the energy components in the global integral of the two reanalysis datasets was about 5 %, while the discrepancy between the conversion components was about 16 %, with the exception of C(P_M, K_M) (see Figs. 1, 2, 3). Generally, the differences between the two reanalysis datasets were larger in the JJA season than in the DJF season. Furthermore, in the latitude-altitude cross-section, the difference between the two reanalysis datasets in the southern hemisphere was larger than in the northern hemisphere, indicating that the main differences originated from the southern hemisphere. These results are similar to the difference between NCEP R2 and other reanalysis datasets (ERA-40 and JRA-25) reported previously (Marques et al. 2010). We calculated the conversion rates of mean available potential energy to mean kinetic energy [C(P_M, K_M)] and eddy available potential energy to eddy kinetic energy [C(P_E, K_E)] using two formulations (the so-called ‘v·grad z’ and ‘ω·α’ formulations) for the two reanalysis datasets. The differences in the conversion rates for the two reanalysis datasets with respect to the global integral were not appreciable for the two formulations, although some differences were observed on the regional scale. This indicates that these two reanalysis data sets are consistent with each other.

Recently, several research institutions have released reanalysis datasets such as JRA-25 and ERA-Interim. Additionally, Intergovernmental Panel on Climate Change (IPCC) AR4 (fourth assessment report) scenario data are now accessible online, and the IPCC AR5 (fifth assessment report) scenario data will soon be available. The time variation of the energy cycle, including trends and decadal time scales, should be analyzed in future studies, and various reanalysis datasets and scenario data should be compared.

Appendix

 

Symbol	Description
a	Average radius of the earth
$c_{p}$	Specific heat at constant pressure
dm	Mass element, equal to $a^{2} \cos \phi d\lambda d\phi dp/g$
g	Acceleration due to gravity
p	Pressure
R	Gas constant for dry air
t	Time
T	Temperature
u	Zonal wind component (positive: eastward)
v	Meridional wind component (positive: northward)
z	Geopotential height
$\alpha$	Specific volume
$\gamma$	Stability factor, equal to $- \left( {\frac{\theta }{T}} \right)\left( {\frac{R}{{c_{p} p}}} \right)\left( {\frac{{\partial \tilde{\theta }}}{\partial p}} \right)^{ - 1}$
$\lambda$	Geographic longitude
$\phi$	Geographic latitude
$\theta$	Potential temperature
$\kappa$	Kappa equal to $\frac{R}{C_{p} }$
$\omega$	Vertical velocity (positive: downward)
$\left\langle X \right\rangle$	Time average of X, equal to $\frac{1}{{t_{2} - t_{1} }}\int_{{t_{1} }}^{{t_{2} }} {xdt}$
$X'$	Deviation from the time average of X, equal to $X - \left\langle X \right\rangle$
$\left[ X \right]$	Zonal average of X, equal to $\frac{1}{2\pi }\int_{0}^{2\pi } {xd\lambda }$
$X^{*}$	Deviation from the zonal average of X, equal to $X - \left[ X \right]$
$\tilde{X}$	Area average of X over a closed pressure surface equal to $\frac{1}{4\pi }\int_{0}^{2\pi } {\int_{{ - \frac{\pi }{2}}}^{{\frac{\pi }{2}}} {a\cos \phi d\phi d\lambda } }$
$X^{\prime \prime }$	Deviation from the global average of X, equal to $X - \tilde{X}$

• Zonal mean available potential energy

  $$ {\text{P}}_{\text{M}} = \frac{{c_{p} }}{2}\int {\gamma \left[ {\left\langle T \right\rangle } \right]^{\prime \prime 2} {\text{dm,}}} $$

  (7)

• Eddy (transient + stationary) available potential energy

  $$ {\text{P}}_{\text{E}} = {\text{P}}_{\text{TE}} + {\text{P}}_{\text{SE}} = \frac{{c_{p} }}{2}\int {\gamma \left[ {\left\langle {T^{\prime 2} } \right\rangle + \left\langle T \right\rangle^{*2} } \right]{\text{ dm,}}} $$

  (8)

• Zonal mean kinetic energy

  $$ {\text{K}}_{\text{M}} = \frac{1}{2}\int {\left( {\left[ {\left\langle u \right\rangle } \right]^{2} + \left[ {\left\langle v \right\rangle } \right]^{2} } \right)} {\text{ dm,}} $$

  (9)

• Eddy (transient + stationary) kinetic energy

  $$ {\text{K}}_{\text{E}} = {\text{K}}_{\text{TE}} + {\text{K}}_{\text{SE}} = \frac{1}{2}\int {\left( {\left[ {\left\langle {u^{\prime 2} } \right\rangle + \left\langle {v^{\prime 2} } \right\rangle } \right]} \right){\text{ dm}}} + \frac{1}{2}\int {\left( {\left[ {\left\langle u \right\rangle^{*2} + \left\langle v \right\rangle^{*2} } \right]} \right) \, } {\text{dm,}} $$

  (10)

• Conversion from P_M to P_E

  $$ \begin{aligned} {\text{C(P}}_{\text{M}} , {\text{ P}}_{\text{E}} )& {\text{ = C(P}}_{\text{M}} , {\text{ P}}_{\text{TE}} ) {\text{ + C(P}}_{\text{M}} , {\text{ P}}_{\text{SE}} )\\ & = - c_{p} \int {\gamma \left[ {\left( {\left\langle {v^{\prime } T^{\prime } } \right\rangle + \left\langle v \right\rangle^{*} \left\langle T \right\rangle^{*} } \right)} \right]\frac{{\partial \left[ {\left\langle T \right\rangle } \right]}}{a\partial \phi }} {\text{dm}} \\ & \quad - c_{p} \int {p^{ - \kappa } \left[ {\left( {\left\langle {\omega^{\prime } T^{\prime } } \right\rangle + \left\langle \omega \right\rangle^{*} \left\langle T \right\rangle^{*} } \right)} \right]} \frac{{\partial \left( {\gamma p^{\kappa } \left[ {\left\langle T \right\rangle } \right]^{\prime \prime } } \right)}}{a\partial \phi }{\text{dm,}} \\ \end{aligned} $$

  (11)

• Conversion from P_E to K_E

  $$ \begin{aligned} {\text{C(P}}_{\text{E}} , {\text{ K}}_{\text{E}} )& = {\text{ C(P}}_{\text{TE}} , {\text{ K}}_{\text{TE}} ) {\text{ + C(P}}_{\text{SE}} , {\text{ K}}_{\text{SE}} )\\ & = - \int {g\left[ {\left\langle {\frac{{u^{\prime } \partial z^{\prime } }}{a\cos \phi \partial \lambda }} \right\rangle + \left\langle {\frac{{v^{\prime } \partial z^{\prime } }}{a\partial \varphi }} \right\rangle } \right]{\text{dm}} - \int {g\left[ {\frac{{\left\langle u \right\rangle^{*} \partial \left\langle z \right\rangle^{*} }}{a\cos \phi \partial \lambda } + \frac{{\left\langle v \right\rangle^{*} \partial \left\langle z \right\rangle^{*} }}{a\partial \phi }} \right]{\text{dm,}}} } \\ & = - \int {\left[ \left\langle {\omega^{\prime } \alpha^{\prime } } \right\rangle \right]{\text{dm}}} - \int {\left[ {\left\langle \omega \right\rangle^{*} \left\langle \alpha \right\rangle^{*} } \right]{\text{dm,}}} \\ \end{aligned} $$

  (12)

• Conversion from K_E to K_M

  $$ \begin{aligned} {\text{C(K}}_{\text{E}} , {\text{ K}}_{\text{M}} )& = {\text{ C(K}}_{\text{TE}} , {\text{ K}}_{\text{M}} ) {\text{ + C(K}}_{\text{SE}} , {\text{ K}}_{\text{M}} )\\ & = \int {\left[ {\left\langle {u^{\prime } v^{\prime } } \right\rangle + \left\langle u \right\rangle^{*} \left\langle v \right\rangle^{*} } \right]\cos \phi \frac{{\partial \left( {\left[ {\left\langle u \right\rangle } \right]/\cos \phi } \right)}}{a\partial \phi }{\text{dm}}} + \int {\left[ {\left\langle {v^{\prime 2} } \right\rangle + \left\langle v \right\rangle^{*2} } \right]\frac{{\partial \left[ {\left\langle v \right\rangle } \right]}}{a\partial \phi }{\text{dm}}} \\ & \quad + \int {\left[ {\left\langle {\omega^{\prime } u^{\prime } } \right\rangle + \left\langle \omega \right\rangle^{*} \left\langle u \right\rangle^{*} } \right]\frac{{\partial \left[ {\left\langle u \right\rangle } \right]}}{\partial p}{\text{dm}} + \int {\left[ {\left\langle {\omega^{\prime } v^{\prime } } \right\rangle + \left\langle \omega \right\rangle^{*} \left\langle v \right\rangle^{*} } \right]\frac{{\partial \left[ {\left\langle v \right\rangle } \right]}}{\partial p}{\text{dm}}} } \\ & \quad - \int {\left[ {\left\langle v \right\rangle } \right]\left[ {u^{\prime 2} + \left\langle u \right\rangle^{*2} } \right]\frac{\tan \phi }{a}{\text{dm,}}} \\ \end{aligned} $$

  (13)

• Conversion from P_M to K_M

  $$ {\text{C(P}}_{\text{M}} , {\text{ K}}_{\text{M}} ) = - \int {\left[ {\left\langle v \right\rangle } \right]g\frac{{\partial \left[ {\left\langle z \right\rangle } \right]}}{a\partial \phi }{\text{dm,}}} = - \int {\left[ {\left\langle \omega \right\rangle } \right]^{\prime \prime } \left[ {\left\langle \alpha \right\rangle } \right]^{\prime \prime } {\text{dm,}}} $$

  (14)

• Conversion from P_SE to P_TE

  $$ {\text{C(P}}_{\text{SE}} , {\text{ P}}_{\text{TE}} ) = - c_{p} \int {\gamma \left[ {\frac{{\left\langle {u^{\prime } T^{\prime } } \right\rangle^{*} }}{a\cos \phi }\frac{{\partial \left\langle T \right\rangle^{*} }}{\partial \lambda } + \frac{{\left\langle {v^{\prime } T^{\prime } } \right\rangle^{*} }}{a}\frac{{\partial \left\langle T \right\rangle^{*} }}{\partial \phi }} \right]{\text{dm,}}} $$

  (15)

• Conversion from K_SE to K_TE

  $$ \begin{aligned} {\text{C}}({\text{K}}_{\text{SE}} , {\text{ K}}_{\text{TE}} ) & = - \int {\frac{{\left\langle {u^{\prime } u^{\prime } } \right\rangle^{*} }}{a\cos \phi }\frac{{\partial \left\langle u \right\rangle^{*} }}{\partial \lambda }{\text{dm}} - \int {\frac{{\left\langle {u^{\prime } v^{\prime } } \right\rangle^{*} }}{a}\cos \phi \frac{{\partial \left( {\left\langle u \right\rangle^{*} /\cos \phi } \right)}}{\partial \phi }{\text{dm}}} } \\ & \quad \, - \int {\frac{{\left\langle {u^{\prime } v^{\prime } } \right\rangle^{*} }}{a\cos \phi }\frac{{\partial \left\langle v \right\rangle^{*} }}{\partial \lambda }{\text{dm}} - \int {\frac{{\left\langle {v^{\prime } v^{\prime } } \right\rangle^{*} }}{a}\frac{{\partial \left\langle v \right\rangle^{*} }}{\partial \phi }{\text{dm}}} } \\ & \quad \, + \int {\left[ {\left\langle {u^{\prime } u^{\prime } } \right\rangle^{*} \left\langle {v^{\prime } } \right\rangle^{*} } \right]\frac{\tan \phi }{a}{\text{dm}},} \\ \end{aligned} $$

  (16)