Degree-Light-Free Graphs and Hamiltonian Cycles

Abstract.

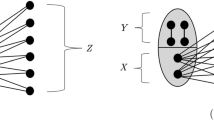
 Let G and H be graphs. G is said to be degree-light H-free if G is either H-free or, for every induced subgraph K of G with K≅H, and every {u,v}⊆K, d i s t _K (u,v)=2 implies max {d(u),d(v)}≥|V(G)|/2. In this paper, we will show that every 2-connected graph with either degree-light {K _1,3, P ₆}-free or degree-light {K _1,3, Z}-free is hamiltonian (with three exceptional graphs), where P ₆ is a path of order 6 and Z is obtained from P ₆ by adding an edge between the first and the third vertex of P ₆ (see Figure 1).