Nonparametric kernel estimation of CVaR under $\alpha$-mixing sequences

Abstract

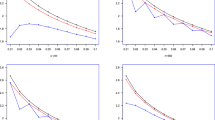
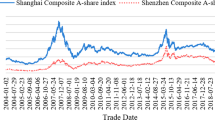
Conditional Value-at-Risk (CVaR) is an increasingly popular coherent risk measure in financial risk management. In this paper, a new nonparametric kernel estimator of CVaR is established, and a Bahadur type expansion of the estimator is also given under $\alpha$-mixing sequences. Furthermore, the mean, variance, mean square error (MSE) and uniformly asymptotic normality of the new estimator are discussed, optimal bandwidths are obtained as well. In order to better illustrate performances of the new CVaR estimator, we conduct numerical simulations under some $\alpha$-mixing sequences and a GARCH model, and discover that the new CVaR estimator is smoother and more accurate than estimators proposed by other scholars because of the bias and MSE of the new estimator are smaller. Finally, we use the new estimator to analyze the daily log-loss of real financial series.

Appendices

Appendix A: Related lemmas and proofs of Theorem 1−3

1.1 Related lemmas of Theorem 1

Lemma 1

(Shao 1990) Suppose $\{X_n, n\ge 1\}$ is a stationary $\alpha$-mixing sequence with $EX_1=0$, $E|X_1|^r<\infty$ for some $r>2$, and

$$\begin{aligned} \alpha (n)=O(n^{-r/(r-2)-\varepsilon }),\ \ \varepsilon >0, \end{aligned}$$

then,

$$\begin{aligned} \limsup _{n\rightarrow \infty }|S_n|/(2n\log \log n)^{1/2}\rightarrow 1\ \ \ \ a.s., \end{aligned}$$

where $S_n=\sum _{t=1}^{n}X_t$.

Denote

$$\begin{aligned} F_n(x)=\frac{1}{n}\sum _{i=1}^{n}I(X_i\le x). \end{aligned}$$

(A.1)

Lemma 2

If the Assumptions 1–4 are satisfied, then

$$\begin{aligned} F_n(x)=F(x)+O\left( n^{-1/2}(\log \log n)^{1/2}\right) ,\ \ a.s. \end{aligned}$$

Proof

Denote $Z_i=I(X_i\le x)-EI(X_i\le x)$. Note $EI(X_i\le x)=F(x)$, then $F_n(x)-F(x)=n^{-1}\sum _{i=1}^{n}Z_i$, and it is clear that $E|Z_i|^{2+\delta }\le 1$. Moreover, since $\alpha (n)=O(n^{-\lambda })$ for $\lambda >(2+\delta )/\delta$, let $\varepsilon =\lambda -(2+\delta )/\delta >0$, then

$$\begin{aligned} \alpha (n)=O(n^{-\lambda })=O(n^{-(2+\delta )/\delta -\varepsilon }). \end{aligned}$$

From Lemma 1, we have

$$\begin{aligned} F_n(x)-F(x)=O\left( n^{-1/2}(\log \log n)^{1/2}\right) ,\ \ a.s. \end{aligned}$$

$\square$

Lemma 3

(Liu 2008) If the Assumptions 1–4 are satisfied, then

$$\begin{aligned} \hat{v}_{p,h}-{v}_{p}=o\left( n^{-1/2}\log n\right) ,\ \ a.s. \end{aligned}$$

Lemma 4

(Liu 2008) Suppose the Assumptions 1–4 are satisfied, denote $b_K=\int _{-\infty }^{+\infty }uK(u)G(u)du$, $\sigma ^2_K=\int _{-\infty }^{+\infty }u^2K(u)du$, and the probability density function of $X_i$ is denoted by $f(\cdot )$, then

$$\begin{aligned} E(\hat{v}_{p,h})= & {} {v}_{p}-\frac{1}{2}h^2f'(v_p)f^{-1}(v_p)\sigma ^2_K+o(h^2),\\ Var(\hat{v}_{p,h})= & {} n^{-1}f^{-2}(v_p)\sigma ^{2}(p; n)+2n^{-1}hf^{-1}(v_p)b_K+o(n^{-1}h). \end{aligned}$$

Let $MSE(\hat{v}_{p,h})=E(\hat{v}_{p,h}-{v}_{p})^2$ be the mean square error (MSE) of $\hat{v}_{p,h}$, then

$$\begin{aligned} MSE(\hat{v}_{p,h})= & {} \frac{1}{nf^2(v_p)}\sigma ^{2}(p; n)+\frac{2}{nf(v_p)}hb_K\nonumber \\&+\,\frac{1}{4}h^4f'^2(v_p)f^{-2}(v_p)\sigma ^4_K +o\left( \frac{h}{n}+h^4\right) . \end{aligned}$$

(A.2)

Lemma 5

Suppose the Assumptions 1–4 are satisfied, then

$$\begin{aligned} \hat{\mu }_{p,h} ={v}_{p}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})^{+}+(\hat{v}_{p,h}-{v}_{p})\cdot o\left( n^{-\frac{1}{2}}\log n\right) ,\ \ a.s. \end{aligned}$$

Proof

$$\begin{aligned} \hat{\mu }_{p,h}= & {} \hat{v}_{p,h}+\frac{1}{np}\sum _{i=1}^{n}[X_i-\hat{v}_{p,h}]^{+} \nonumber \\= & {} \hat{v}_{p,h}+\frac{1}{np}\sum _{i=1}^{n}[X_i-{v}_{p}+{v}_{p}-\hat{v}_{p,h}]^{+} \nonumber \\= & {} \hat{v}_{p,h}+\frac{1}{np}\sum _{i=1}^{n}({v}_{p}-\hat{v}_{p,h})I(X_i>\hat{v}_{p,h})\nonumber \\&+\,\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})I(X_i>\hat{v}_{p,h})\nonumber \\= & {} \hat{v}_{p,h}+({v}_{p}-\hat{v}_{p,h})\frac{1}{np}\sum _{i=1}^{n}I(X_i>\hat{v}_{p,h})\nonumber \\&+\,\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})I(X_i>\hat{v}_{p,h}) \nonumber \\= & {} \hat{v}_{p,h}+({v}_{p}-\hat{v}_{p,h})\frac{1}{p}[1-F_n(\hat{v}_{p,h})]\nonumber \\&+\,\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})I(X_i>\hat{v}_{p,h})\nonumber \\:= & {} \hat{v}_{p,h}+J_1+J_2. \end{aligned}$$

(A.3)

Note $\hat{v}_{p,h}-v_p=o(n^{-1/2}\log n)$ a.s. and $F_n(x)=F(x)+O(n^{-1/2}(\log \log n)^{1/2})$, then there exists $0<\theta <1$ such that

$$\begin{aligned} J_1= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ 1-F(\hat{v}_{p,h})+O\left( n^{-1/2}(\log \log n)^{1/2}\right) \right] \nonumber \\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\Bigg [1-F(v_p)-f(v_p+\theta (\hat{v}_{p,h}-v_p))(\hat{v}_{p,h}-v_p)\nonumber \\&\qquad \qquad \qquad +\,O\left( n^{-1/2}(\log \log n)^{1/2}\right) \Bigg ]\nonumber \\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ 1-(1-p)+o(n^{-1/2}\log n)+\,O\left( n^{-1/2}(\log \log n)^{1/2}\right) \right] \nonumber \\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ p+o\left( n^{-1/2}\log n\right) \right] \nonumber \\= & {} {v}_{p}-\hat{v}_{p,h}+(\hat{v}_{p,h}-v_p)\cdot o\left( n^{-1/2}\log n\right) ,\ \ \ \ a.s., \end{aligned}$$

(A.4)

then from Formula (A.3) and (A.4), it’s clear that

$$\begin{aligned} \hat{\mu }_{p,h}={v}_{p}+(\hat{v}_{p,h}-v_p)\cdot o(n^{-1/2}\log n)+J_2,\ \ \ \ a.s. \end{aligned}$$

(A.5)

More over,

$$\begin{aligned} J_2= & {} \frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})\left[ I(X_i>\hat{v}_{p,h})-I(X_i>{v}_{p})\right] \nonumber \\&+\,\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})I(X_i>{v}_{p})\nonumber \\:= & {} J_{21}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})I(X_i>{v}_{p}). \end{aligned}$$

(A.6)

Since

$$\begin{aligned}&|X_i-{v}_{p}|\cdot \left[ I(X_i>\hat{v}_{p,h})-I(X_i>{v}_{p})\right] \\&\quad =\big |(X_i-{v}_{p})\cdot [I(\hat{v}_{p,h}<X_i\le {v}_{p})I(\hat{v}_{p,h}<{v}_{p})\\&\qquad -I({v}_{p}<X_i\le \hat{v}_{p,h})I({v}_{p}<\hat{v}_{p,h})]\big |\\&\quad \le |\hat{v}_{p,h}-{v}_{p}|\cdot [I(\hat{v}_{p,h}<X_i\le {v}_{p})I(\hat{v}_{p,h}<{v}_{p})\\&\qquad +\,I({v}_{p}<X_i\le \hat{v}_{p,h})I({v}_{p}<\hat{v}_{p,h})]. \end{aligned}$$

Then,

$$\begin{aligned} |J_{21}|\le & {} \frac{1}{np}\sum _{i=1}^{n}|\hat{v}_{p,h}-{v}_{p}|\big [I(\hat{v}_{p,h}<X_i\le {v}_{p})I(\hat{v}_{p,h}<{v}_{p})\\&\qquad \qquad \qquad \qquad \qquad \;+\,I({v}_{p}<X_i\le \hat{v}_{p,h})I({v}_{p}<\hat{v}_{p,h})\big ]\\= & {} \frac{1}{p}|\hat{v}_{p,h}-{v}_{p}|\Big \{\big [F_n({v}_{p})-F_n(\hat{v}_{p,h})\big ]I(\hat{v}_{p,h}<{v}_{p})\\&\qquad \qquad \qquad \qquad +\,\big [F_n(\hat{v}_{p,h})-F_n({v}_{p})I({v}_{p}<\hat{v}_{p,h})\big ]\Big \}\\\le & {} \frac{1}{p}|\hat{v}_{p,h}-{v}_{p}||F_n(\hat{v}_{p,h})-F_n({v}_{p})|\\= & {} \frac{1}{p}|\hat{v}_{p,h}-{v}_{p}|\Big |F({v}_{p})+f(v_p+\theta (\hat{v}_{p,h}-v_p))(\hat{v}_{p,h}-v_p)-F({v}_{p})\\&\qquad \qquad \qquad \qquad +\,O\left( n^{-\frac{1}{2}}(\log \log n)^{\frac{1}{2}}\right) \Big |\\= & {} \frac{1}{p}|\hat{v}_{p,h}-{v}_{p}|\cdot \left| o\left( n^{-\frac{1}{2}}\log n\right) \right) \left. +\,O\left( n^{-\frac{1}{2}}(\log \log n)^{\frac{1}{2}}\right) \right| \\= & {} |\hat{v}_{p,h}-{v}_{p}|\cdot o\left( n^{-\frac{1}{2}}\log n\right) . \end{aligned}$$

It implies that

$$\begin{aligned} J_{21}=(\hat{v}_{p,h}-{v}_{p})\cdot o(n^{-\frac{1}{2}}\log n). \end{aligned}$$

(A.7)

Combining Formula (A.5), (A.6) with (A.7), we have

$$\begin{aligned} \hat{\mu }_{p,h} ={v}_{p}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})^{+}+(\hat{v}_{p,h}-{v}_{p})\cdot o\left( n^{-\frac{1}{2}}\log n\right) . \end{aligned}$$

$\square$

Lemma 6

Suppose the Assumptions 1–4 are satisfied, then

$$\begin{aligned} o\left( n^{-\frac{1}{2}}\log n\right) (\hat{v}_{p,h}-v_p)\le & {} \hat{\mu }_{p,h}-\left[ {v}_{p}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})^+\right] \\\le & {} \frac{2}{p}f(v_p)(\hat{v}_{p,h}-v_p)^2+o\left( n^{-\frac{1}{2}}\log n\right) (\hat{v}_{p,h}{-}v_p),\ \ a.s. \end{aligned}$$

Proof

Note $\hat{v}_{p,h}-v_p=O(n^{-1/2}\log n)$ a.s. and $F_n(x)=F(x)+o(n^{-1/2}\log n)$, then in the Eq. (A.3)

$$\begin{aligned} J_1= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ 1-F(\hat{v}_{p,h})+o\left( n^{-1/2}\log n\right) \right] \\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\Bigg [1-F(v_p)-f(v_p)(\hat{v}_{p,h}-v_p)\\&\qquad \qquad \qquad -\frac{1}{2}f(v_p+\theta (\hat{v}_{p,h}-v_p))(\hat{v}_{p,h}-v_p)^2+o\left( n^{-1/2}\log n\right) \Bigg ]\\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ 1-(1-p)-f(v_p)(\hat{v}_{p,h}-v_p)+o\left( n^{-1}\log ^2 n\right) \right. \\&\qquad \qquad \qquad \left. +\,o\left( n^{-1/2}\log n\right) \right] \\= & {} \frac{{v}_{p}-\hat{v}_{p,h}}{p}\left[ p-f(v_p)(\hat{v}_{p,h}-v_p)+o\left( n^{-1/2}\log n\right) \right] \\= & {} {v}_{p}-\hat{v}_{p,h}+p^{-1}f(v_p)(\hat{v}_{p,h}-v_p)^2+o(n^{-1/2}\log n)(\hat{v}_{p,h}-v_p),\ \ \ \ a.s. \end{aligned}$$

From Formula (A.3), we have

$$\begin{aligned} \hat{\mu }_{p,h}={v}_{p}+p^{-1}f(v_p)(\hat{v}_{p,h}-v_p)^2+o(n^{-1/2}\log n)(\hat{v}_{p,h}-v_p)+J_2,\ \ \ \ a.s.\nonumber \\ \end{aligned}$$

(A.8)

Moreover,

$$\begin{aligned}&(X_i-{v}_{p})\left[ I(X_i>\hat{v}_{p,h})-I(X_i>{v}_{p})\right] \\&\quad =(X_i-{v}_{p})[I({v}_{p}<X_i<\hat{v}_{p,h})+I(\hat{v}_{p,h}<X_i<{v}_{p})], \end{aligned}$$

then

$$\begin{aligned} (\hat{v}_{p,h}-{v}_{p})I(\hat{v}_{p,h}<X_i<{v}_{p})\le & {} (X_i-{v}_{p})\left[ I(X_i>\hat{v}_{p,h})-I(X_i>{v}_{p})\right] \\\le & {} (\hat{v}_{p,h}-{v}_{p})I({v}_{p}<X_i<\hat{v}_{p,h}). \end{aligned}$$

Then, $J_{21}$ of Formula (A.6) satisfies

$$\begin{aligned}&\frac{1}{np}\sum _{i=1}^{n}(\hat{v}_{p,h}-{v}_{p})I(\hat{v}_{p,h}<X_i<{v}_{p})\nonumber \\&\quad \le J_{21}\le \frac{1}{np}\sum _{i=1}^{n}(\hat{v}_{p,h}-{v}_{p})I({v}_{p}<X_i<\hat{v}_{p,h}),\nonumber \\&\frac{1}{p}(\hat{v}_{p,h}-{v}_{p})[F_n({v}_{p})-F_n(\hat{v}_{p,h})]\le J_{21}\le \frac{1}{p}(\hat{v}_{p,h}-{v}_{p})[F_n(\hat{v}_{p,h})-F_n({v}_{p})],\nonumber \\&\frac{1}{p}(\hat{v}_{p,h}-{v}_{p})\left[ F({v}_{p})-F(\hat{v}_{p,h})+o\left( n^{-\frac{1}{2}}\log n\right) \right] \nonumber \\&\quad \le J_{21}\le \frac{1}{p}(\hat{v}_{p,h}-{v}_{p})\left[ F(\hat{v}_{p,h})-F({v}_{p})+o\left( n^{-\frac{1}{2}}\log n\right) \right] ,\nonumber \\&\frac{1}{p}(\hat{v}_{p,h}-{v}_{p})\left[ f(v_p)(v_p-\hat{v}_{p,h})+o\left( n^{-\frac{1}{2}}\log n\right) \right] \nonumber \\&\quad \le J_{21}\le \frac{1}{p}(\hat{v}_{p,h}-{v}_{p})\left[ f(v_p)(\hat{v}_{p,h}-v_p)+o\left( n^{-\frac{1}{2}}\log n\right) \right] . \end{aligned}$$

(A.9)

Combining Formula (A.3), (A.6), (A.8) with (A.9), we have

$$\begin{aligned}&o(n^{-\frac{1}{2}}\log n)(\hat{v}_{p,h}-v_p)\le \hat{\mu }_{p,h}-\left[ {v}_{p}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})^+\right] \\&\quad \le \frac{2}{p}f(v_p)(\hat{v}_{p,h}-v_p)^2+o\left( n^{-\frac{1}{2}}\log n\right) (\hat{v}_{p,h}-v_p). \end{aligned}$$

$\square$

From Lemma 5, Theorems 1 and 2 can be easily proved as follows.

1.2 Proof of Theorem 1

Proof

Since ${\hat{v}}_{p,h}-{v}_{p}=o(n^{-1/2}\log n),\ a.s.$, then $({\hat{v}}_{p,h}-{v}_{p})\cdot o(n^{-1/2}\log n)=o(n^{-1}\log ^2 n),\ a.s.$ So, from Lemma 5 we have

$$\begin{aligned} \hat{\mu }_{p,h} ={v}_{p}+\frac{1}{np}\sum _{i=1}^{n}(X_i-{v}_{p})^{+}+o(n^{-1}\log ^2 n),\ \ a.s. \end{aligned}$$

$\square$

1.3 Proof of Theorem 2

Proof

From Lemma 4, we know that $E(\hat{v}_{p,h}-v_p)=O(h^2)$. Moreover, using the result of Lemma 5, we have

$$\begin{aligned} E(\hat{\mu }_{p,h})= & {} {v}_{p}+\frac{1}{np}\sum _{i=1}^{n}E(X_i-{v}_{p})^{+}+E(\hat{v}_{p,h}-{v}_{p})\cdot o\left( n^{-\frac{1}{2}}\log n\right) \\= & {} {\mu }_{p}+o\left( n^{-\frac{1}{2}}h^2\log n\right) . \end{aligned}$$

Besides, Formula $Var(\hat{\mu }_{p,h})=p^{-2}n^{-1}\sigma ^2_0(p; n)+o(n^{-2}\log ^4n)$ is obvious from Theorem 1. Therefore,

$$\begin{aligned} MSE(\hat{\mu }_{p,h})= & {} E[\hat{\mu }_{p,h}-\mu _{p}]^2=Var(\hat{\mu }_{p,h})+[E(\hat{\mu }_{p,h})-\mu _{p}]^2\\= & {} p^{-2}n^{-1}\sigma ^2_0(p; n)+o(n^{-2}\log ^4n+n^{-1}h^4\log ^2 n). \end{aligned}$$

$\square$

1.4 Proof of Theorem 3

Proof

From Lemma 4, we know that $E(\hat{v}_{p,h}-v_p)=O(h^2)$. Utilizing the result of Lemma 6, we have

$$\begin{aligned} o\left( n^{-\frac{1}{2}}h^2\log n\right)\le & {} E\hat{\mu }_{p,h}-\left[ {v}_{p}+\frac{1}{np}\sum _{i=1}^{n}E(X_i-{v}_{p})I(X_i>{v}_{p})\right] \\\le & {} \frac{2}{p}f(v_p)E(\hat{v}_{p,h}-v_p)^2+o\left( n^{-\frac{1}{2}}h^2\log n\right) ,\\ o\left( n^{-\frac{1}{2}}h^2\log n\right)\le & {} E\hat{\mu }_{p,h}-\left[ {v}_{p}+\frac{1}{p}E(X-{v}_{p})I(X>{v}_{p})\right] \\\le & {} \frac{2}{p}f(v_p)MSE(\hat{v}_{p,h})+o\left( n^{-\frac{1}{2}}h^2\log n\right) ,\\ o\left( n^{-\frac{1}{2}}h^2\log n\right)\le & {} E\hat{\mu }_{p,h}-{\mu }_{p}\\\le & {} \frac{2}{p}f(v_p)MSE(\hat{v}_{p,h})+o\left( n^{-\frac{1}{2}}h^2\log n\right) . \end{aligned}$$

It means that

$$\begin{aligned} |E\hat{\mu }_{p,h}-{\mu }_{p}| \le \frac{2}{p}f(v_p)MSE(\hat{v}_{p,h})\left| o\left( n^{-\frac{1}{2}}h^2\log n\right) \right| . \end{aligned}$$

So, Theorem 3 holds. $\square$

Appendix B: Related lemmas and proof of Theorem 4

In this section, we give some necessary lemmas and the proof of Theorem 4.

1.1 Related lemmas of Theorem 4

Lemma 7

(Roussas and Ioannides 1987) Let $\{X_i:i\ge 1\}$ be a sequence of $\alpha$-mixing random variables. Suppose that $\xi$ and $\eta$ are ${\mathcal {F}}_{1}^{k}$-measurable and ${\mathcal {F}}_{k+n}^{\infty }$-measurable random variables, respectively. If $E|\xi |^s<\infty$, $E|\eta |^t<\infty \ \ a.s.$, and $1/s+1/t+1/q=1$, then

$$\begin{aligned} |E\xi \eta -E\xi E\eta |\le 10\alpha ^{1/q}(n)\Vert \xi \Vert _{s}\Vert \eta \Vert _{t}, \end{aligned}$$

where, $\Vert Y\Vert _r:=(E|Y|^r)^{1/r}.$

Note 1

There exists a positive number C such that $|\sigma ^2_0(p; n)|<C$ for any $n\ge 1$. Actually, let $q=(2+\delta )/\delta$ and $s=t=(2+\delta )$ in Lemma 7, then from Assumption 1, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }|\sigma ^2_0(p; n)|\le & {} Var\{[X_1-v_p]^+\}\\&+\,2\sum ^{\infty }_{k=1}\left( 1-\frac{k}{n}\right) |Cov\{[X_1-v_p]^+,[X_{k+1}-v_p]^+\}|\\\le & {} Var\{[X_1-v_p]^+\}\\&+\,2\sum ^{\infty }_{k=1}10\alpha ^{\delta /(2+\delta )}(n)\cdot \Vert [X_1-v_p]^+\Vert _{2+\delta }\cdot \Vert [X_{k+1}-v_p]^+\Vert _{2+\delta }\\\le & {} Var\{[X_1-v_p]^+\}+C\sum ^{\infty }_{k=1}\alpha ^{\delta /(2+\delta )}(n)<\infty . \end{aligned}$$

Lemma 8

(Yang 2000) Let $\{X_j : j\ge 1\}$ be a sequence of $\alpha$-mixing random variables with zero mean.

• (i) If $E|X_j|^{2+\delta }<\infty$ for $\delta >0$, then

  $$\begin{aligned} E\left( \sum _{j=1}^{n}X_j\right) ^2\le \left( 1+20\sum _{m=1}^n\alpha ^{\delta /(2+\delta )}(m)\right) \sum _{j=1}^n\Vert X_j\Vert _{2+\delta }^2. \end{aligned}$$

• (ii) If $E|X_j|^{r+\tau }<\infty$ and $\alpha (n)=O(n^{-\lambda })$ for $r>2$, $\tau >0$ and $\lambda >r(r+\tau )/2\tau$, then, for given $\varepsilon >0$, there exists a positive constant $C=C(r,\tau ,\lambda ,\varepsilon )$ which doesn’t depend on n such that

  $$\begin{aligned} E\left| \sum _{j=1}^{n}X_j\right| ^r\le C\left\{ n^{\varepsilon }\sum _{j=1}^nE|X_j|^r+\left( \sum _{j=1}^n\Vert X_j\Vert _{r+\tau }^2\right) ^{r/2}\right\} . \end{aligned}$$

Denote $Y_{i}:={n^{-1/2}}\sigma _{0}^{-1}(p, n)\{[X_i-v_p]^+ -E[X_i-v_p]^+\}$, $i=1,2,\ldots ,n$, and $S_n:=\sum _{i=1}^{n}Y_{i}$, then

$$\begin{aligned} U_n= & {} \sqrt{n}p\sigma _{0}^{-1}(p, n)\{\hat{\mu }_{p,h}-\mu _p\}\nonumber \\= & {} \sqrt{n}p\sigma _{0}^{-1}(p, n)\left\{ v_p+\frac{1}{np}\sum _{i=1}^{n}[X_i-v_p]^+\,o(n^{-1}\log ^2n) -v_p\right. \nonumber \\&\qquad \qquad \qquad \qquad \quad -\,\left. \frac{1}{np}\sum _{i=1}^{n}E[X_i-v_p]^+\right\} \nonumber \\= & {} {n^{-1/2}}\sigma _{0}^{-1}(p, n)\sum _{i=1}^{n}\{[X_i-v_p]^+ -E[X_i-v_p]^+\}+o\big (n^{-1/2}\log ^2n\big )\nonumber \\= & {} S_n+o(n^{-1/2}\log ^2n). \end{aligned}$$

(B.1)

At first, we prove that $S_n$ is uniformly asymptotic normality.

Let $k=\lfloor n/(p_1+p_2)\rfloor$, then

$$\begin{aligned} S_n=S_{1n}+S_{2n}+S_{3n}, \end{aligned}$$

(B.2)

where,

$$\begin{aligned} S_{1n}= & {} \sum _{m=1}^{k}y_{nm},S_{2n}=\sum _{m=1}^{k}y_{nm}^{\prime },S_{3n}=y_{nk+1}^{\prime },\\ y_{nm}= & {} \sum _{i=k_m}^{k_m+p_1-1}Y_{i},y_{nm}^{\prime }=\sum _{i=l_m}^{l_m+p_2-1}Y_{i},y_{nk+1}^{\prime }=\sum _{i=k(p_1+p_2)+1}^{n}Y_{i}, \end{aligned}$$

$k_m=(m-1)(p_1+p_2)+1,l_m=(m-1)(p_1+p_2)+p_1+1,m=p_2,\ldots ,k.$

Lemma 9

Suppose Assumptions 1–5 are satisfied, then

$$\begin{aligned} E|S_{2n}|^2\le & {} C\gamma _{1n},~E|S_{3n}|^2\le C\gamma _{2n}, \end{aligned}$$

(B.3)

$$\begin{aligned} P(|S_{2n}|\ge \gamma _{1n}^{1/3})\le & {} C\gamma _{1n}^{1/3},~P(|S_{3n}|\ge \gamma _{2n}^{1/3})\le C\gamma _{2n}^{1/3}. \end{aligned}$$

(B.4)

Proof

From Lemma 8(i), Assumption 1 , Formula (3.1) and Note 1, we know

$$\begin{aligned} E|S_{2n}|^2\le & {} C\sum _{m=1}^{k}\sum _{i=k_m}^{k_m+p_2-1}n^{-1}\sigma _0^{-2}(p, n) \le Ckp_2n^{-1}\nonumber \\\le & {} C\frac{n}{p_1+p_2}p_2n^{-1} \le C\frac{1}{1+p_2p_1^{-1}}p_2p_1^{-1}=C\gamma _{1n}. \end{aligned}$$

On the other hand, $n-k(p_1+p_2)<(p_1+p_2)$, then

$$\begin{aligned} E|S_{3n}|^2\le & {} C\sum _{i=k(p_1+p_2)+1}^{n}n^{-1}\sigma _0^{-2}(p, n) \le C(n-k(p_1+p_2))n^{-1} \\\le & {} C(p_1+p_2)n^{-1} \le C(1+p_2p_1^{-1})p_1 n^{-1} = C\gamma _{2n}. \end{aligned}$$

So Formula (B.3) holds. Otherwise, Formula (B.4) can be proved by combining the Markov inequality with Formula (B.3). $\square$

Denote $s_n^2:=\sum _{m=1}^k Var(y_{nm})$, we can obtain an inequality about $s_n^2$ as follows.

Lemma 10

Suppose Assumptions 1–5 are satisfied, then

$$\begin{aligned} |s_n^2-1|\le C\left( \gamma _{1n}^{1/2}+\gamma _{2n}^{1/2}+u(p_2)\right) . \end{aligned}$$

Proof

Note $E|S_n|^2=Var(S_n)=1$, and

$$\begin{aligned} s_n^2=E|S_{1n}|^2-2\sum _{1\le i<j\le k}Cov(y_{ni},y_{nj}), \end{aligned}$$

Then, using Lemma 9, we have

$$\begin{aligned} |E|S_{1n}|^2-1|= & {} \big |E[S_n-(S_{2n}+S_{3n})]^2\big |\nonumber \\= & {} \big |E(S_{2n}+S_{3n})^2-2E[S_n(S_{2n}+S_{3n})]\big |\nonumber \\\le & {} E|S_{2n}+S_{3n}|^2+2E|S_n(S_{2n}+S_{3n})|\nonumber \\\le & {} 2\big (E|S_{2n}|^2+E|S_{3n}|^2\big )+2\big (E|S_n|^2\big )^{1/2}\big (E|S_{2n}+S_{3n}|^2\big )^{1/2}\nonumber \\\le & {} C\big (E|S_{2n}|^2+E|S_{3n}|^2+(E|S_{2n}|^2\big )^{1/2}+\big (E|S_{3n}|^2)^{1/2}\big )\nonumber \\\le & {} C\big (\gamma _{1n}^{1/2}+\gamma _{2n}^{1/2}\big ). \end{aligned}$$

(B.5)

Moreover,

$$\begin{aligned} \Big |\sum _{1\le i<j\le k}Cov(y_{ni},y_{nj})\Big |\le & {} \sum _{1\le i<j\le k}\sum _{s=k_i}^{k_i+p_1-1}\sum _{t=k_j}^{k_j+p_1-1}|Cov(Y_{s},Y_{t})|\nonumber \\\le & {} \sum _{1\le i<j\le k}\sum _{s=k_i}^{k_i+p_1-1}\sum _{t=k_j}^{k_j+p_1-1}n^{-1}\sigma _0^{-2}(n, p)\alpha ^{\delta /(2+\delta )}(t-s)\nonumber \\\le & {} C\sum _{i=1}^{k-1}\sum _{s=k_i}^{k_i+p_1-1}n^{-1}\sum _{j=i+1}^{k}\sum _{t=k_j}^{k_j+p_1-1}\alpha ^{\delta /(2+\delta )}(t-s)\nonumber \\\le & {} C\sum _{s=1}^{n}n^{-1}\sum _{j=p_2}^{\infty }\alpha ^{\delta /(2+\delta )}(j) \le Cu(p_2). \end{aligned}$$

(B.6)

Combining Formula (B.5) with (B.6), we know Lemma 10 holds. $\square$

Suppose $\{\xi _{nm}:m=1,2,\ldots ,k\}$ is an independent random variable sequence, random variables $\xi _{nm}$ and $y_{nm}$ are identically distributed ($m=1,2,\ldots ,k$). Let $T_n=\sum _{m=1}^k \xi _{nm}, D_n=\sum _{m=1}^k Var(\xi _{nm})$, and denote $H_n(u)$ and $\tilde{H}_n(u)$ as the distribution functions of $T_n/\sqrt{D_n}$ and $T_n$, respectively. Obviously,

$$\begin{aligned} D_n=s_n^2,~\tilde{H}_n(u)=H_n(u/s_n). \end{aligned}$$

Lemma 11

Suppose Assumptions 1–5 are satisfied, then

$$\begin{aligned} \sup _u|H_n(u)-\Phi (u)|\le C\gamma _{2n}^{\rho }. \end{aligned}$$

(B.7)

Proof

Let $r=2+2\rho$ and $\tau =\delta -2\rho$. From Formula (3.4), we have $0<2\rho <\delta$, then $\tau =\delta -2\rho >0$, moreover,

$$\begin{aligned} \frac{r(r+\tau )}{2\tau }=\frac{(1+\rho )(2+\delta )}{\delta -2\rho }<\lambda . \end{aligned}$$

Using Lemma 8(ii) and taking $\varepsilon =\rho$, we have

$$\begin{aligned} \sum _{m=1}^k E|y_{nm}|^{2+2\rho }\le & {} C\sum _{m=1}^k \left\{ p_1^{\rho }\sum _{i=k_m}^{k_m+p_1-1}E|Y_{i}|^{2+2\rho }+\left( \sum _{i=k_m}^{k_m+p_1-1}\Vert Y_{i}\Vert _{2+\delta }^{2} \right) ^{1+\rho }\right\} \\\le & {} C\left\{ p_1^{\rho }\sum _{m=1}^k\sum _{i=k_m}^{k_m+p_1-1}n^{-(1+\rho )}+\sum _{m=1}^k\left( \sum _{i=k_m}^{k_m+p_1-1}n^{-1} \right) ^{1+\rho }\right\} \\\le & {} C\left\{ p_1^{\rho }\sum _{i=1}^n n^{-(1+\rho )}+\sum _{m=1}^kp_1^{\rho }\sum _{i=k_m}^{k_m+p_1-1}n^{-(1+\rho )}\right\} \\\le & {} C\left\{ p_1^{\rho }n^{-\rho }+p_1^{\rho }n^{-\rho }\right\} \le C \gamma _{2n}^{\rho }. \end{aligned}$$

And using Lemma 10, we know $D_n^2=s_n^2\rightarrow 1$, hence

$$\begin{aligned} \frac{1}{D_n^{1+\rho }}\sum _{m=1}^k E|\xi _{nm}|^{2+2\rho }\le C\gamma _{2n}^{\rho }. \end{aligned}$$

Utilizing Berry–Esseen theorem, we obtain Formula (B.7). $\square$

Lemma 12

(Yang 2003) Suppose $\{\xi _n:n\le 1\}$ and $\{\eta _n:n\le 1\}$ are two random variable sequences, and positive constant sequence $\{\gamma _n:n\le 1\}$ satisfies $\gamma _n\rightarrow 0$ as $n\rightarrow \infty$. If

$$\begin{aligned} \sup _u|F_{\xi _n}(u)-\Phi (u)|\le C\gamma _n, \end{aligned}$$

then for $\forall$$\epsilon >0$,

$$\begin{aligned} \sup _u|F_{\xi _n+\eta _n}(u)-\Phi (u)|\le C\{\gamma _n+\epsilon +P(|\eta _n|\ge \epsilon )\}. \end{aligned}$$

1.2 Proof of Theorem 4

Proof

Using similar proof methods of Yang and Li (2006, Theorem 2.1 and Lemma 4.4), we easily have

$$\begin{aligned} \sup _{u}\left| {F}_{S_n}(u)-\Phi (u)\right| \le C\left\{ \gamma _{1n}^{1/3}+\gamma _{2n}^{1/3}+\gamma _{2n}^{\rho }+\gamma _{3n}^{1/4}+u(p_2)\right\} . \end{aligned}$$

(B.8)

Moreover, applying Lemma 12 by taking $\epsilon =n^{-1/4}\log n$ and Formula (B.1), (B.8), we know Theorem 4 holds. $\square$

1.3 Proof of Corollary 2

The proof of this corollary is similar to that of Yang and Li (2006, Corollary 2.3).