Abstract
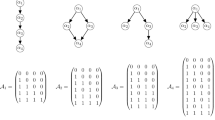
Educational researchers have argued that a realistic view of the role of attributes in cognitively diagnostic modeling should account for the possibility that attributes are not isolated entities, but interdependent in their effect on test performance. Different approaches have been discussed in the literature; among them the proposition to impose a hierarchical structure so that mastery of one or more attributes is a prerequisite of mastering one or more other attributes. A hierarchical organization of attributes constrains the latent attribute space such that several proficiency classes, as they exist if attributes are not hierarchically organized, are no longer defined because the corresponding attribute combinations cannot occur with the given attribute hierarchy. Hence, the identification of the latent attribute space is often difficult—especially, if the number of attributes is large. As an additional complication, constructing a complete Q-matrix may not at all be straightforward if the attributes underlying the test items are supposed to have a hierarchical structure. In this article, the conditions of identifiability of the latent space if attributes are hierarchically organized and the conditions of completeness of the Q-matrix are studied.
Access this article
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.
Similar content being viewed by others
References
BIRKHOFF, G. (1970), Lattice Theory, New York: Macmillan.
CHIU, C.-Y., and KÖ HN, H.-F. (2015), “Consistency of Cluster Analysis for Cognitive Diagnosis: The DINO Model and the DINAModel Revisited”, Applied Psychological Measurement, 39, 465–479.
CHIU, C.-Y., DOUGLAS, J.A., and LI, X. (2009), “Cluster Analysis for Cognitive Diagnosis: Theory and Applications”, Psychometrika, 74, 633–665.
DE LA TORRE, J. (2011), “The Generalized Dina Model Framework”, Psychometrika, 76, 179–199.
DE LA TORRE, J., and DOUGLAS, J.A. (2004), “Higher-Order Latent Trait Models for Cognitive Diagnosis”, Psychometrika, 69, 333–353.
DIBELLO, L.V., ROUSSOS, L.A., and STOUT, W.F. (2007), “Review of Cognitively Diagnostic Assessment and a Summary of Psychometric Models”, in Handbook of Statistics: Vol. 26. Psychometrics, eds. C.R. Rao and S. Sinharay, Amsterdam: Elsevier, pp. 979–1030.
FU, J., and LI, Y. (2007), “An Integrative Review of Cognitively Diagnostic Psychometric Models”, paper presented at the April Annual Meeting of the National Council on Measurement in Education, Chicago, IL.
HABERMAN, S.J., and VON DAVIER, M. (2007), “Some Notes on Models for Cognitively Based Skill Diagnosis”, in Handbook of Statistics: Vol. 26. Psychometrics, eds. C.R. Rao and S. Sinharay, Amsterdam: Elsevier, pp. 1031–1038.
HAERTEL, E.H. (1989), “Using Restricted Latent Class Models to Map the Skill Structure of Achievement Items”, Journal of Educational Measurement, 26, 333–352.
HAERTEL, E.H., and WILEY, D.E. (1994), “Representation of Ability Structure: Implications for Testing”, in Testing Theory for a New Generation of Tests, eds. N. Fredriksen, R. Mislevy, and I. Bejar, Hillsdale, NJ: Erlbaum, pp. 359–384.
HARARY, F., NORMAN, R.Z., and CARTWRIGHT, D. (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
HEIJMANS, H.J.A.M. (1994), Morphological Image Operators, Boston, MA: Academic Press/Harcourt, Brace and Company, Publishers.
HENSON, R.A., TEMPLIN, J.L., and WILLSE, J.T. (2009), “Defining a Family of Cognitive Diagnosis Models Using Log-Linear Models with Latent Variables”, Psychometrika, 74, 191–210.
HUBERT, L.J. (1974), “Some Applications of Graph Theory to Clustering”, Psychometrika, 39, 283–309.
JUNKER, B.W., and SIJTSMA, K. (2001), “Cognitive Assessment Models with Few Assumptions, and Connections with Nonparametric Item Response Theory”, Applied Psychological Measurement, 25, 258–272.
KÖ HN, H.-F., and CHIU, C.-Y. (2017), “A Procedure for Assessing the Completeness of the Q-Matrices of Cognitively Diagnostic Tests”, Psychometrika, 82(1), 112–132.
LEIGHTON, J., and GIERL, M. (2007), Cognitive Diagnostic Assessment for Education: Theory and Applications, Cambridge, UK: Cambridge University Press.
LEIGHTON, J.P., GIERL, M.J., and HUNKA, S. (2004), “The Attribute Hierarchy Model: An Approach for Integrating Cognitive Theory with Assessment Practice”, Journal of Educational Measurement, 41, 205–236.
MACREADY, G.B., and DAYTON, C.M. (1977), “The Use of Probabilistic Models in the Assessment of Mastery”, Journal of Educational Statistics, 33, 379–416.
MARIS, E. (1999), “Estimating Multiple Classification Latent Class Models”, Psychometrika, 64, 187–212.
RUPP, A.A., TEMPLIN, J.L., and HENSON, R.A. (2010), Diagnostic Measurement. Theory, Methods, and Applications, New York: Guilford.
RUPP, A.A., and TEMPLIN, J.L. (2008), “Effect of Q-matrix Misspecification on Parameter Estimates and Misclassification Rates in the DINA Model”, Educational and Psychological Measurement, 68, 78–96.
TATSUOKA, K.K. (1985), “A Probabilistic Model for Diagnosing Misconception in the Pattern Classification Approach”, Journal of Educational and Behavioral Statistics, 12, 55–73.
TATSUOKA, K.K. (2009), Cognitive Assessment. An Introduction to the Rule Space Method, New York: Routledge/Taylor and Francis.
TEMPLIN, J.L., and HENSON, R.A. (2006), “Measurement of Psychological Disorders Using Cognitive Diagnosis Models”, Psychological Methods, 11, 287–305.
TEMPLIN, J., and BRADSHAW, L. (2014), “Hierarchical Diagnostic Classification Models: A Family of Models for Estimating and Testing Attribute Hierarchies”, Psychometrika, 79, 317–339.
VON DAVIER, M. (2005), “A General Diagnostic Model Applied to Language Testing Data”, Research Report No. RR-05-16, September, Princeton, NJ: Educational Testing Service.
VON DAVIER, M. (2008), “A General Diagnostic Model Applied to Language Testing Data”, British Journal of Mathematical and Statistical Psychology, 61, 287–301.
Author information
Authors and Affiliations
Corresponding author
Additional information
This material is based upon work supported by the National Science Foundation under Grant No. 1552563.
Rights and permissions
About this article
Cite this article
Köhn, HF., Chiu, CY. Attribute Hierarchy Models in Cognitive Diagnosis: Identifiability of the Latent Attribute Space and Conditions for Completeness of the Q-Matrix. J Classif 36, 541–565 (2019). https://doi.org/10.1007/s00357-018-9278-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00357-018-9278-6