1 Introduction

The combined measurement of velocity and scalar fields such as concentration, density, pressure and temperature in gaseous flows is of utmost importance for the understanding of complex aerodynamic or thermofluid systems. Typical laser-diagnostic measurement approaches for acquiring these correlated data involve the application of particle image velocimetry (PIV) for planar velocity measurements combined with laser induced fluorescence (LIF), laser induced phosphorescence (LIP), liquid crystal thermometry or filtered Rayleigh scattering (FRS) to simultaneously obtain at least one scalar quantity such as temperature or concentration (Most et al. 2002; Su and Mungal 2004; Jainski et al. 2014; Schreivogel et al. 2016; Lee et al. 2016; McManus and Sutton 2020; Straußwald et al. 2020; Mommert et al. 2023). While a body of literature exists for combined velocity and temperature or concentration measurements, only a single article describes a method to obtain velocity and pressure fields from an oxygen partial pressure measurement combining PIV and luminescence lifetime imaging of pressure sensitive paint (PSP) particles (Abe et al. 2004). All of the previously mentioned approaches have in common that they require extensive hardware and, more importantly, involve the addition of dedicated tracer particles or molecules, which generally demands thorough calibration procedures and significantly narrows the applicability of these techniques. Considering the complexities of current diagnostic concepts, an immediate demand for simpler and more universal approaches becomes apparent.

One of the few laser-optical methods that do not require the addition of a flow tracer is the filtered Rayleigh scattering (FRS) technique (Miles and Lempert 1990). Combined with a frequency scanning technique (Forkey 1996; Boguszko and Elliott 2005; Doll et al. 2014), FRS has the proven ability to simultaneously measure time-averaged pressure, temperature and velocity fields in application-oriented test facilities with limited optical accessibility (Doll et al. 2014, 2017a; Schroll et al. 2017; Doll et al. 2018). In addition, the combined measurement of three-component (3C) velocity fields with planar pressure and temperature was achieved by observing the measurement plane from three different sides (Doll et al. 2017b). This demonstrates the inherent capabilities of the FRS technique for a comprehensive characterisation of aerothermal flows, whereby it must be emphasised that the tracer free non-intrusive planar measurement of pressure fields is unique.

A disadvantage of previous multi-property measurements by FRS is that the frequency scanning used so far is a time consuming data acquisition mode and can only provide time-averaged results. In this regard, the extension of FRS to the planar measurement of multiple time-resolved flow quantities is the “panacea” to be attained (Ground et al. 2023). In order to extend the FRS technique to time-resolved multi-property measurements, one idea is to split the scattering signal obtained from a single laser pulse between several detection channels, each equipped with a molecular filter of different vapour density (Miles and Lempert 1990a; Boguszko 2003; Yeaton et al. 2012; George et al. 2016; Jenkins et al. 2019). A second approach involves using a single molecular filter in combination with at least five directions of observation to derive the five unknown flow variables (pressure, temperature and three velocity components) from a single laser pulse measurement (Doll et al. 2022a). The latter approach leads to an elaborate detection scheme that has recently been optimised to maximise sensitivities of an instantaneous multi-property FRS measurement based on a six view observation concept (Doll et al. 2022b). It is the aim of this work to experimentally verify this diagnostic approach by performing FRS measurements with an optimised multiple-view detection scheme on a simple aspirated pipe flow. To this end, FRS measurements are conducted using continuous wave (CW) laser illumination to provide both high-quality time-averaged results based on frequency scanning as well as to perform a quasi-time-resolved data analysis based on single-frequency processing.

The principle idea behind the time-resolved multi-parameter FRS measurement combining various perspective views is briefly explained in Sect. 2. Therein, the theoretical optimisation process leading to an optical setup offering the highest flow parameter sensitivities as well as the basic data processing concept are described. The flow experiment, the FRS instrumentation based on CW laser illumination and the optimised detection scheme are presented in Sect. 3. The post-processing of the multi-view FRS data in time-averaged and time-resolved evaluation mode is outlined in Sect. 4. In addition, results obtained from a straight and a swirling pipe flow are presented and discussed. The article ends with some concluding remarks and future perspectives.

Fig. 1
figure 1

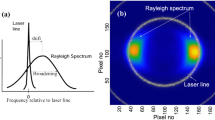
a Orientation of the six optimised camera views on a sphere around the region of interest. b Top Simulated FRS intensity spectra normalised by the available Rayleigh scattering (RS) for a frequency scan around the 18788.44 cm\(^{-1}\)-doublet for the six optimised camera views. The scattering angles \(\theta\) and \(\phi\) are indicated in the legend. Bottom FRS signal intensities at the optimised single-pulse wavenumber \(\nu _\textrm{opt}\)

Full size image

2 Multiple-view FRS

The acquired intensities \(S_k\) from an FRS measurement in a single-component gas atmosphere can be described using the following equation (Forkey 1996; Miles et al. 2001; Doll et al. 2014, 2017b)

$$\begin{aligned} S_{k}&= C_k I_\textrm{0} n \sin ^2\!\phi _k \nonumber \\&\quad \int \limits _{-\infty }^{\infty } r_k \left( \nu -\nu _\textrm{0},p,T,\vec {\textrm{v}},\theta _k\right) \tau (\nu ) \textrm{d}\nu + B_k. \end{aligned}$$
(1)

The index k indicates the different viewing perspectives, C is a constant specific to the optical setup, \(I_\textrm{0}\) the incident laser power, n the number density, and \(\phi\) is the angle spanned by the observation and the polarisation direction of the laser. The following integral expression is the convolution between Rayleigh lineshape r and the transmission curve of the molecular filter \(\tau\). It incorporates the signal’s dependencies on the excitation frequency \(\nu _0\), the flow variables pressure p, temperature T and velocity \(\vec {\textrm{v}}\) as well as another geometry parameter \(\theta\), which is the angle between observation and laser direction. The constant B is introduced to account for background intensities that originate from an incomplete suppression of laser stray light by the molecular filter.

The general idea behind the simultaneous measurement of multiple instantaneous flow parameters from different perspective views builds on a further development of the FRS velocimetry approach outlined in Doll et al. (2017b). There, three linearly independent directions of observation were combined with frequency scanning to measure time-averaged 3C velocity, pressure and temperature fields in a jet flow. By scanning the laser’s output frequency along the molecular filter’s transmission curve, Eq. 1 is transformed into a significantly over-determined mathematical problem, from which the five flow variables were obtained with high accuracy using nonlinear regression. In contrast, a multi-view FRS measurement based on a single laser pulse with a single output frequency must rely on a notably lower amount of data, corresponding to the number of available camera perspectives.

In our recently published work (Doll et al. 2022b), it is argued that in a single-frequency multi-view FRS arrangement, it is not sufficient to place the different camera perspectives randomly in the space around the experiment. Instead, multi-objective optimisation is used to identify a suitable optical configuration to target the lowest possible measurement uncertainties for all flow quantities. In addition to the previous approach that focussed solely on the scattering geometry, the excitation frequency is added as an optimisation parameter here as well.

Fig. 2
figure 2

a Schematic of the aspirated pipe flow facility. The inset on the right shows a photograph of the axial swirler. b Enlarged view of the test section with light sheet interface

Full size image

A schematic containing the six camera positions, represented by the grey cones, optimised for a representative flow inside the duct is depicted in Fig. 1a. The different perspectives are shown in relation to the direction of the laser light \(\vec{l}\), polarisation direction \(\vec{p}\) and the flow velocity \(\vec {\textrm{v}}\). For the simulation, all views are oriented on a spherical surface with radius R and their positions are defined by the respective polar and azimuthal angles \(\alpha\) and \(\beta\). The laser is aligned at an angle \(\lambda =135\)° to ensure uniformly distributed uncertainties for the in-plane velocity components.

The effect of the resulting scattering geometry on the normalised FRS signal is shown in Fig. 1b, top. Simulations are conducted for different excitation wavenumbers within the blocking range of the molecular filter. All curves have in common that the FRS signal rises with wavenumber, which is related to the double structure of the selected absorption line that leads to a reduced transmitted Rayleigh intensity at lower values. The differences between the curves are related to the variation of the scattering angles \(\theta\) and \(\phi\). \(\theta\) has a pronounced influence on the Rayleigh scattering’s spectral width and shape, whereby the width increases or decreases with magnitude and the portions of the Rayleigh scattering that pass through the molecular filter become correspondingly larger or smaller. \(\phi\) accounts for the Rayleigh scattering’s dipole nature, so that the overall scattered intensity scales with \(\sin ^2\phi\) (Miles et al. 2001).

For an instantaneous FRS measurement at a single excitation frequency, the wavenumber \(\nu _\textrm{opt}\) is identified by the optimiser, which is highlighted by the blue dashed-dotted line in Fig. 1b, top. The corresponding normalised FRS signal intensities are depicted in Fig. 1b, bottom. The choice of that particular wavenumber by the optimiser is potentially motivated by its location close to the end of the blocking region of the molecular filter, where the slope of the transmission curve increases rapidly and changes in the Rayleigh scattering’s spectral shape due to temperature or pressure and Doppler shifts from flow velocity lead to strong dynamics of the FRS intensity. The actual flow regime affects the expected flow parameter sensitivities, and the wavenumber selected by the optimiser offers a good compromise for the anticipated flow conditions. More detailed information about the multi-variate dependency of the FRS signal on the wavenumber, the scattering angles as well as the optimised detection configuration can be found in Doll et al. (2022b).

Fig. 3
figure 3

a Principle layout of the FRS system. b Close-up image of a fibre bundle exit illuminated with an integrating sphere. c Photograph of the FRS instrumentation installed at the flow facility. d Snapshot of a calibration target observed through the six-branch image fibre bundle

Full size image

3 Flow configuration and FRS instrumentation

The pipe flow configuration is chosen to facilitate a proof of concept for the multi-view FRS instrument to characterise internal flow systems. A schematic of the flow facility is shown in Fig. 2a. The test rig is designed for a bulk streamwise velocity of up to 100 m/s at the test section. Air is sucked into a bell-shaped inlet nozzle manufactured using 3D printing. For initial flow conditioning, a honeycomb flow straightener and three meshes are installed in front of the inlet nozzle to reduce velocity fluctuations to about 1% of the mean flow velocity. The incurred pressure drop \(\textrm{d}p\) over the inlet nozzle is closely related to the flow rate; laser Doppler anemometry (LDA) measurements are used to yield an empirical calibration of the resulting velocities against \(\textrm{d}p\), which in turn corresponds to a certain rotational speed of the suction fan. In this work, three operating points corresponding to \(\textrm{d}p=5.0\), 23.1 and 60.6 hPa are investigated. In the swirled flow configuration, an axial swirler (inset on the right in Fig. 2a) and another straight pipe of about 7 diameter length are introduced before the measurement plane to allow for a certain degree of flow development.

A close-up view of the test section is shown in Fig. 2b. It consists of a light sheet interface and a precision borosilicate glass pipe of 500 mm length and 80 mm internal diameter. To introduce the laser into the test section, the light sheet interface aims at minimising laser scattering and reflections off glass surfaces: a tiny gap is left between the inlet pipe and the glass channel, which is surrounded by a sealed housing with plane windows on the input and output flanges. The laser enters through the gap and illuminates the cross section of the flow channel, which can then be observed from different perspectives from the downstream side.

As outlined in the introduction, the current work focuses on verifying the optimised detection setup of Fig. 1a. To this end, a continuous wave (CW) instead of a pulsed laser is applied to reduce system complexity. The general layout of the FRS implementation is shown schematically in Fig. 3a. The system is based on a narrow-linewidth AzurLight (CW) fibre laser, emitting green laser light at a wavelength of 532 nm. The laser has an adjustable output power ranging from 0.1 to 6 W, here operated at 5 W, and a spectral bandwidth below 200 kHz, which is accomplished through an external NKT Photonics ADJUSTIK Y10 seed laser unit. The latter features two options for tuning the output frequency: fast piezo tuning in the range of 10 GHz around the central wavelength and slow thermal tuning over 700 GHz (compared to 60 GHz of the previously used Coherent Verdi system in Doll et al. (2014)). A small portion of laser light is coupled into the wavelength monitoring and control unit through a single-mode fibre (smf) behind the laser exit. This light is used as an input signal for the frequency stabilisation of the laser, which is based on a HighFinesse WS-8 wavelength-meter (wlm), achieving a relative stability of the laser’s output frequency below 1 MHz to the set-point. Since changing environmental conditions may lead to a drift of the frequency measurement, the device is repeatedly calibrated using a narrow-linewidth, frequency stabilised helium-neon laser. As the Rayleigh scattering signal depends on the incident laser intensity, the latter is continuously monitored by a power metre (pm). Subsequently, the laser beam is guided through an articulated mirror arm (ama) and expanded into a light sheet using an optical scanner arrangement (lsg). A half-wave plate (\(\lambda /2\)) is used to adjust the polarisation of the laser to lie within the x–y-plane (cf. Fig. 1a).

Light scattered from the plane of interest is collected with a six-branch image fibre bundle (ifb). The front end of each branch is equipped with a camera lens having a focal length of 16 mm and \(f_\#=1.4\), imaging the observed region on a light sensitive area of 4 \(\times\) 4 mm\(^{2}\) (400 \(\times\) 400 fibre elements @ 10 \(\upmu\)m fibre diameter). A close-up image of the output of an image fibre bundle branch observing the illuminated output side of an integrating sphere can be seen in Fig. 3b. The image shows the typical structure of a leached fibre bundle with individual fibres containing the signal intensities surrounded by dark light insensitive cladding. Each branch has a length 2500 mm such that the different perspectives can be conveniently aligned in the space around the test section.

A photograph of the FRS instrumentation installed at the flow facility is shown in Fig. 3c. When reproducing the optimised optical setup shown in Fig. 1a, hydraulic magnetic measuring stands are used to fix the different perspectives in their respective positions. To align the six fibre bundle front ends to the optimised coordinates, the individual positions are projected onto the wooden screen in the background and strings are drawn from these points towards the centre of the measurement plane. Then, the respective branch is fixed at the specified radius R from this reference point. A comparison between the optimised and the installed perspective angles is provided in Table 1. In Doll et al. (2022b), it was found that an angular misalignment of \(\pm\, 5\)° has an acceptable effect on measurement accuracy. Since only two perspectives show slightly higher differences for the azimuthal angle \(\beta\), this is not expected to cause a dominant detrimental effect.

Table 1 Comparison of optimised (Opt) and installed (Exp) camera positions
Full size table

The individual observation branches are combined at the back-end of the image fibre bundle, resulting in a rectangular shaped area of 12 mm height and 8 mm width (3 \(\times\) 2 square regions, each representing a single camera view). As shown in Fig. 3a, two lenses in retro-arrangement (l1, l2) form the transfer optics and pass the light collected by the fibre bundle branches through a molecular iodine filter cell (ic) and a bandpass filter (bpf, FWHM 10 nm), the latter blocking both broadband background light and iodine fluorescence. With the second camera lens (l2), the filtered light is focussed on the camera sensor (PCO Edge 4.2). A sample camera image with a calibration target located at the light sheet plane inside the flow duct is shown in Fig. 3d. For all FRS measurements, the camera is operated with a 4 \(\times\) 4 binning and 20 s exposure time for an individual image. A raw FRS image acquired at the optimised wavenumber is shown in Fig. 4.

Fig. 4
figure 4

Raw FRS image acquired at the optimised wavenumber of 18,788.455 cm\(^{-1}\)

Full size image
Fig. 5
figure 5

Image transformation of perspective #4 from camera coordinate system (a, blue cross) to world coordinate system (b, red plus). c Parts of the duct (black, solid) are obstructed from view. The number of views having optical access to a particular area is indicated by the contours

Full size image

4 Data processing and results

4.1 Image processing and data analysis

A dataset obtained by the multiple-view imaging FRS instrument consists of (1) a set of calibration images to determine the camera positions and to map the different perspectives onto a common Cartesian grid; (2) reference image data acquired with known pressure and temperature (ambient conditions) and zero flow velocity to obtain an optical calibration constant, a background parameter and a zero Doppler shift to account for the absolute accuracy of the wavelength-meter (10 MHz) and frequency-dependent transmission properties of the bandpass filter at each resolution element; (3) Data obtained under flow conditions. For both reference and flow datasets, frequency scanning at 37 discrete frequencies was performed and measurements were repeated five times and averaged to further increase signal-to-noise-ratio (SNR). To evaluate the FRS data, the transmission curve of the absorption filter is required, which has been calibrated in advance with a photodiode arrangement with an accuracy of \({<0.5}\)%.

The automated identification of the six camera positions relies on Python’s OpenCV toolbox (Bradski 2000) and will not be discussed here. The post-processing starts with subdividing the calibration image of Fig. 3d into six parts, each representing a single perspective. For all these views, a dewarping procedure is applied to transform the different perspectives to a predefined coordinate system represented by a calibration plate with a regular dot-pattern introduced at the light sheet plane. The procedure is demonstrated for the calibration image of perspective #4 in Fig. 5a (warped) and 5b (dewarped). As a result, each resolution element in world coordinates covers an area of 1 \(\times\) 1 mm\(^{2}\) and contains the information of the six perspectives. Depending on the viewing angle, the optical access to the measuring plane is partially blocked by the housing of the light sheet flange as outlined in Sect. 3, which is visualised in Fig. 5c. The red zone represents the visible area common to all views, covering over 78% of the total cross section.

Fig. 6
figure 6

Top Evaluation of FRS intensity spectra obtained from frequency scanning for a single super-resolution element. Each colour represents a different perspective. The measured FRS intensities (crosses) are fitted with the model equation (solid) to derive pressure, temperature and u, v, w velocity components (fit result in the box). Bottom Residuals of the data fit

Full size image

Before performing any step of the FRS processing chain, the raw images are smoothed with a 3 \(\times\) 3 averaging filter to reduce the spatial noise introduced by the fibre structure of the image fibre bundle. By referring to the reference data set, the optical calibration constant C and background parameter B of Eq. 1 as well as a zero Doppler shift are determined for each resolution element. This is done separately for each camera perspective relying on established methodology (Doll et al. 2014, 2016). While for the frequency scanning analysis the complete sweep of available frequencies is used, the experimental parameters in case of the quasi-time-resolved analysis are obtained from a reduced number of frequencies \(\pm 0.004\) cm\(^{-1}\) around \(\nu _\textrm{opt}\).

For analysing the data gathered under flow conditions, the measurements from all perspectives are combined and jointly evaluated. For the frequency scanning analysis, data is processed as long as a minimum of three perspectives have optical access to the respective resolution element. This is true for almost the total cross section except for a small area in the upper left corner of the duct in Fig. 5c. For the quasi-time-resolved evaluation, processing is confined to the area which can be accessed by all six perspectives.

To simultaneously derive time-averaged pressure, temperature and the three velocity components from the frequency scanning data, a nonlinear fit of the model Eq. 1 is carried out so that the flow quantities are obtained at each super-resolution element (37 scanning frequencies x 6 perspectives). The result of the fitting procedure for a single super-resolution element is shown in Fig. 6, top. Measurement data are obtained at two neighbouring absorption lines, leading to a two-branch structure with a frequency gap in between. The resulting intensity spectra for each perspective strongly differ in level and shape, which is mainly related to the variation in scattering geometry and its influence on the Rayleigh lineshape and signal strength (Doll et al. 2022b). The Rayleigh lineshape model used in this work is a combination of a calibrated analytical model (Doll et al. 2016) and a recently introduced machine learning approximation (Hunt et al. 2020). In contrast to the previous approach in Doll et al. (2017b), where the Doppler frequencies were fitted and the 3C velocity field was subsequently reconstructed, here, the Doppler formula is coupled with the simulation of the FRS intensities. This has the distinct advantage that the maximum number of unknown flow parameters is fixed to five, regardless of the number of perspectives, whereas when fitting Doppler shifts, the number of unknowns increases with the number of perspectives. The residuals of the fitting procedure shown in Fig. 6, bottom, demonstrate the very good quality of the fit and are of the order of 0.7% of the FRS intensity averaged over all frequencies.

Fig. 7
figure 7

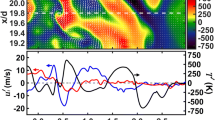
Comparison of time-averaged and quasi-time-resolved maps of the straight pipe flow for pressure (a, d), temperature (b, e) and axial velocity maps (c, f) for \(\textrm{d}p=5\) hPa. The in-plane velocity components are represented by the vector fields, only every second vector is shown. The channel boundaries are indicated by the black solid line

Full size image
Fig. 8
figure 8

Radially averaged pressure profiles with \(p_{0}-\textrm{d}p\) (dashed) (a), temperature profiles with isentropic temperature (dashed) (b) and axial velocity profiles (solid) with LDA measurements (circle) (c) for frequency scanning (solid) and quasi-time-resolved data analysis (dashed-dotted) for three operating points denoted by the differential pressure \(\textrm{d}p\). LDA errorbars in (c) indicate the standard deviation of the radial mean velocity per radius

Full size image
Fig. 9
figure 9

Spatial averages (blue, solid) and standard deviations \(\sigma\) (red, dashed-dotted) of the constant core flow region at operating point \(\textrm{d}p=5.0\) hPa plotted against the number of multistage passes (zero means conventional fitting) for p (a), T (b) and w (c). Reference values are represented by the blue dashed lines. Standard deviations \(\sigma _\textrm{MC}\) (red, dotted) are theoretical values computed from Monte Carlo simulations

Full size image

In contrast to frequency scanning, the combined determination of multiple time-resolved flow quantities has to be performed for the single excitation frequency that is obtained from the optimisation together with the six camera perspectives (Fig. 1). As a consequence, the number of available FRS intensities per super-resolution element reduces from 222 (6 perspectives times 37 frequencies) to 6 (6 perspectives times 1 frequency). Due to the significantly reduced amount of data, the resulting flow properties from the single-frequency analysis are much more affected by bias and statistical uncertainties. To address this, a multistage data fitting procedure is developed. The approach makes use of an empirical observation that the velocity components can be derived with high accuracy even without knowledge of the exact thermodynamic properties. Therefore, the multistage procedure starts with fitting the three velocity components only, while pressure and temperature a kept constant at their starting guess. In the next step, the resulting velocities are fed into a second fitting process, wherein the velocities are kept constant while pressure and temperature are adapted. This is repeated until the resulting flow properties converge to a certain value. For the current application it was found that the multistage fitting procedure already yields acceptable results after a single pass only, which might be related to the weak coupling of thermodynamics and aerodynamics for the current flow experiment.

4.2 Straight pipe flow

Pressure, temperature and axial velocity maps determined for the straight pipe flow configuration from both frequency scanning and quasi-time-resolved data processing are shown in Fig. 7. Since small movements of the test section during operation caused changes of the background illumination close to the channel boundaries, results from that region are considered unreliable and not shown. Overall, the results reflect the typical structure of a developing turbulent pipe flow, with constant static pressure and temperature over the entire cross section and a “plug-like” axial velocity distribution, with constant values in the centre and a velocity gradient towards the channel walls. The pressure field in Fig. 7a shows a weak non-physical structure; however, the spatial variation lies on average below 0.5% of the corresponding mean pressure over the cross section.

Comparing the frequency scanning against quasi-time-resolved results, the latter appear more grainy, Fig. 7a–c versus 7d–f. This is related to higher measurement uncertainties, which are to be expected considering the significantly smaller amount of data that have been used for the quasi-time-resolved processing. While the increase in spatial variability is less pronounced in the pressure fields, it becomes quite evident in the temperature and axial velocity maps. In addition to the axial velocity component w, the velocity maps in Fig. 7c and f also contain the in-plane components u and v indicated by the vectors. For the straight pipe flow where no lateral flow velocity exists, the randomly oriented velocity vectors in Fig. 7c are an expression of the velocity uncertainty of the method. For the quasi-time-resolved results in Fig. 7f, the vector field exhibits a directional tendency towards the upper left that might be related to uncertainties in the camera perspectives and associated projection errors.

Fig. 10
figure 10

Comparison of time-averaged and quasi-time-resolved maps of the swirling flow for pressure (a, d), temperature (b, e) and axial velocity maps (c, f) for \(\textrm{d}p=26\) hPa. The in-plane velocity components are represented by the vector fields, only every second vector is shown. The channel boundaries are indicated by the black solid line

Full size image

To further assess the accuracy of the FRS measurements, radially averaged pressure, temperature and axial velocity profiles of the frequency scanning and the quasi-time-resolved analysis are compared to the reference differential pressure \(\textrm{d}p\) measured at the inlet nozzle, the resulting isentropic temperature and corresponding laser Doppler anemometry (LDA) velocity measurements for three different bulk velocities in Fig. 8. Regarding the pressure profiles, average differences between FRS results and the reference values grow with \(\textrm{d}p\) (the flow rate) from 2 to 27 hPa (0.2 to 2.8%) for frequency scanning and 3 to 33 hPa (0.3 to 3.5%) for quasi-time-resolved. Corresponding deviations from isentropic temperatures reach about 3.8 K (1.3%) for the quasi-time-resolved analysis at the highest flow rate, while for the other configurations they stay below 2.1 K (0.7%). The comparison of axial velocities measured by LDA and FRS up to a radial distance of \(r=25\) mm shows an excellent agreement for all operating points and for both data processing methods, with differences lying in between \(\pm 2\) m/s (7 to 2% of maximum velocity). The growing deviations when approaching the channel boundaries can be explained by the differing measurement location, which in case of LDA was 2-3 tube diameters downstream, resulting in a more developed velocity profile with a smaller area of constant velocity near the centre and less steep slopes towards the channel border.

The quasi-time-resolved results of Figs. 7 and 8 are obtained by applying the multistage evaluation approach introduced at the end of Sect. 3, relying on a single pass only. To motivate this choice, an analysis of the mean convergence (accuracy) and precision is carried out against the number of passes through the multistage fitting procedure, Fig. 9. Since the flow is characterised by constant properties in the core region, the spatial standard deviations can be considered representative for the measurement precision of the respective flow quantity. Concerning the spatial averages, convergence can be assumed both for the conventional fitting of all flow parameters at the same time (zero passes) as well as for the variation of the number of passes, since the apparent changes are well within the precision bounds. In contrast, there is a steep drop of the standard deviations when switching from conventional to multistage evaluation from 40 to 2.2 hPa (4 to 0.2%) for pressure, 8.2 to 2.2 K (2.8 to 0.8%) for temperature and 5.3 to 1.7 m/s (18.7 to 6.4%) for axial velocity for a single multistage pass, followed by a slower gradual rise for two and three passes. As for the degradation of the precision after two or more passes, the reason for this behaviour is currently unknown and needs further investigation. While the conventional fitting agrees well with the theoretical values obtained from the Monte Carlo simulations (Doll et al. 2022b) (the slightly lower experimental values are probably related to the initial spatial smoothing of the images), the single pass multistage fitting approach leads to a remarkable improvement in precision by factors of about 3 and 4 for axial velocity and temperature, and 18 for pressure, respectively.

4.3 Swirling flow

Pressure, temperature and velocity maps obtained from the swirling flow configuration are shown in Fig. 10. Since the aforementioned movement of the test section was not as pronounced as for the straight duct experiment, the data could be evaluated up to the channel boundaries. Similar to the straight pipe flow, pressure and temperature are expected to be constant across the entire cross section, which is reflected by both the frequency scanning and quasi-time-resolved results. The frequency scanning results appear smoother due to the overall lower uncertainty, whereby the pressure map exhibits some artifacts at the lower left and upper right channel bounds as well as a diagonal “stripe”, which might still be caused by slight background changes from reference to flow measurement. However, apart from some peak values close to the channel wall, these variations are well within 0.5% of the mean pressure.

Concerning the axial velocity field, the frequency scanning results show regions of velocity deficit at the center and, although weaker, around the circumference, which originate from the wakes of the swirler vanes and the support structure. The influence of the boundary layer causing a steep decline of axial momentum at the channel walls is also well captured. The in-plane velocity components (only every second vector is presented) show a strong swirling motion around the vortex core at the channel axis. The same flow features can also be observed in the quasi-time-resolved velocity results, albeit with correspondingly lesser precision.

5 Conclusions

The combined measurement of multiple time-resolved flow quantities is a difficult task, and the filtered Rayleigh scattering (FRS) technique has emerged as a promising candidate for its solution. In our previous work, we developed an FRS concept for the simultaneous time-resolved measurement of 3C velocity, pressure and temperature fields by detecting the FRS signal from six perspective views. The perspectives were optimised to yield the lowest measurement uncertainties in a time-resolved single-frequency measurement scenario. To verify this concept, this work introduces an FRS instrument based on continuous wave laser illumination that makes use of multiple-branch image fibre bundle technology to realise signal detection from six different perspectives. The instrument is installed at a pipe flow experiment operated in a straight as well as a swirling flow configuration. Frequency scanning is applied to obtain high-quality time-averaged multi-property measurement results. To demonstrate the detection concept for time-resolved measurements, quasi-time resolution is simulated by selecting a single frequency from the frequency scan and performing a multi-parameter analysis on this reduced dataset.

After introducing common processing steps, results of the straight pipe flow experiment are used for an in-depth uncertainty analysis. It is found that frequency scanning can reproduce reference pressures and derived isentropic temperatures within 2.8 and 0.8%, respectively. The quasi-time-resolved data analysis yields corresponding accuracy values of 3.5 and 1.3%. Concerning axial velocity, both processing approaches show excellent agreement with LDA velocity measurements within \(\pm \,2\) m/s (7 to 2% of maximum velocity). Precision of the quasi-time-resolved processing was further analysed considering the area of constant flow properties at the channel axis. By introducing a newly developed multistage fitting procedure, precision of pressure, temperature and velocity results could be improved by factors of 18, 4 and 3 to 2.2 hPa, 2.2 K and 1.7 m/s as compared to the simultaneous fitting of all flow parameters, respectively. The capability of the time-resolved multi-property FRS concept to resolve secondary flow structures was demonstrated in a swirling flow configuration, whereby quasi-time-resolved compare very favourably to high-quality frequency scanning results.

The combined measurement of multiple time-resolved flow quantities by FRS is a long standing goal of the experimental fluid mechanics community, and the outcome of this study represents an important milestone on the way to achieving it. The presented results provide detailed insights into the capabilities of FRS for multi-parameter measurements based on a single excitation frequency. Since the quasi-time-resolved FRS results are the first of their kind, the validity of the reported accuracy and precision beyond the presented flow case needs further assessment. In any case, the quasi-time-resolved analysis delivers encouraging results for this already quite challenging internal flow application, which provides confidence in the methods ability to perform under alternate conditions. Future work will focus on implementing the proposed concept using pulsed laser illumination for the true combined time-resolved measurement of 3C velocity, pressure and temperature fields by FRS.