Mixing characterization of highly underexpanded fluid jets with real gas expansion

Abstract

We report a comprehensive speed of sound database for multi-component mixing of underexpanded fuel jets with real gas expansion. The paper presents several reference test cases with well-defined experimental conditions providing quantitative data for validation of computational simulations. Two injectant fluids, fundamentally different with respect to their critical properties, are brought to supercritical state and discharged into cold nitrogen at different pressures. The database features a wide range of nozzle pressure ratios covering the regimes that are generally classified as highly and extremely highly underexpanded jets. Further variation is introduced by investigating different injection temperatures. Measurements are obtained along the centerline at different axial positions. In addition, an adiabatic mixing model based on non-ideal thermodynamic mixture properties is used to extract mixture compositions from the experimental speed of sound data. The concentration data obtained are complemented by existing experimental data and represented by an empirical fit.

1 Introduction

The injection strategies and resulting mixing processes in engines strongly influence the combustion performance, and, ultimately, the achievable efficiency and pollutant emission (Idicheria and Pickett 2007). Naturally, there is an ecological and economic incentive to make advances in this area which is further encouraged by recent political focus. Therefore, characterization of the fuel injection process is a crucial element of virtually all combustion-based energy conversion systems.

In this context, high system pressures are typically used to facilitate efficient mixing and to provide sufficiently high fuel mass flows. Examples in the automotive industry include the potential benefits for direct injection engines (De Boer et al. 2013), especially with respect to natural gas or hydrogen injection (Hamzehloo and Aleiferis 2014). Furthermore, high injection pressures are an inherent feature of efficient fuel/oxidizer preparation in the conventional direct injection engines (Idicheria and Pickett 2007). For the latter, a pre-heating of the fuel to supercritical temperatures was also found to yield higher engine efficiencies and a simultaneous decrease in emissions (Tavlarides and Antiescu 2009; Anitescu et al. 2012; Whitaker et al. 2011). Similar to hydrogen and natural gas, the fuel, then, features considerable compressibility. Consequently, choked flow conditions are easily reached resulting in the formation of an underexpanded jet downstream of the nozzle. The expansion characteristics are determined by the ratio of reservoir $p_{{\rm inj}}$ to chamber pressure $p_{\rm {ch}}$, typically expressed as nozzle pressure ratio (NPR). Depending on the NPR, the jets are classified as subsonic, moderately, and highly underexpanded.

For highly underexpanded jets, the flow adapts to $p_{\rm {ch}}$ through a single, barrel-shaped shock structure. A common criterion for this classification is the NPR, which is typical four and above (Donaldson and Snedeker 1971) such gases like air, nitrogen, or hydrogen. Furthermore, the flow field and shock system, especially the distance of the normal shock from the nozzle exit, is strongly affected by the NPR (Franquet et al. 2015).

Supercritical fluids are highly compressible and can show significant variation in their thermodynamic properties during the relaxation process to the, often, subcritical $p_{\rm {ch}}$. This, consequently, even influences the mixing process in the far-field zone (Banholzer et al. 2017; Baab et al. 2017).

This complex coupling between thermo- and aerodynamic behavior is challenging for numerical simulations which emerged as an essential design tool for future combustion systems. Consequently, considerable efforts have been made in recent years to develop reliable numerical frameworks (e.g., Banholzer et al. 2017; Hamzehloo and Aleiferis 2016a; Velikorodny and Kudriakov 2012; Vuorinen et al. 2013; Mohamed and Paraschivoiu 2005; Bonelli et al. 2013; Khaksarfard et al. 2010).

Suitable experimental data sets and test cases for validation of such numerical predictions are, however, limited as stated, for instance, in Hamzehloo and Aleiferis (2016a, b). Existing studies usually focus on a particular application, e.g., leakage studies for high-pressure hydrogen storage, e.g., Molkov (2012) or aerospace applications involving very large nozzle diameters (as discussed in Hamzehloo and Aleiferis (2016a)), which do not allow for an universal assessment of the mixing phenomena across the entire range of applications. This study is designed to increase the fundamental understanding of such processes and proposes detailed reference cases for numerical simulations.

In a previous study, we demonstrated that laser-induced thermal acoustics (LITA), also referred to as laser-induced grating spectroscopy (LIGS) is capable of acquiring quantitative data for such applications. It was shown that measurements of small-scale jet mixing processes are feasible despite the turbulent mixing flow and harsh flow field properties. This qualifies the technique as an excellent method to overcome the general lack of experimental data. A full discussion of the advantages of this technique, a comparison to alternative diagnostic tools as well as an overview of existing experimental studies in literature are given in Baab et al. (2016).

The purpose of this study is to apply the technique to generate a comprehensive experimental database. Specifically, it features

• 1. a wide range of NPRs to alter the shock/expansion system,

• 2. injection conditions, such that real gas treatment is mandatory,

• 3. flow and nozzle geometry in the order of $\mathcal {O}\;(100\,\upmu \hbox {m})$ as typically found for internal combustion engines, and

• 4. an application-near surrogate fuel as well as an academically interesting fluid.

The experimental conditions were selected, such that the treatment of real gas effects in the expansion process becomes mandatory.

To the best of our knowledge, this is the first study to provide such extensive and quantitative speed of sound data in this context. This database can be used for the validation of numerical simulations, as it is not biased by any assumption on the mixing mechanism or by the choice of a thermodynamic model. In addition, mixture composition is extracted from the experimental speed of sound data using a mixing model with non-ideal thermodynamic properties. The distinct separation between directly measured data (i.e. speed of sound) and thermodynamically derived quantities (i.e. species concentration) represents, in our opinion, one of the main advantages of the LIGS database. This is particularly relevant for supercritical fluid injection, where the development of accurate EoS and associated mixing rules is still an open field of research.

Ultimately, the obtained mixture compositions lead to an empirical fit for the entire range of injection conditions investigated in this study.

2 Measurement conditions

The injectant is initially stored at supercritical temperature and pressure and discharged into cold nitrogen at ambient pressure. We use two different injectants, an alkane, namely n-hexane (n-$\hbox {C}_{6}\hbox {H}_{14}$, purity $>99\%$), and a fluoroketone (FK-5-1-12, $3\hbox {M}^{\mathrm{TM}}$ Novec 649). Table 1 summarizes the critical properties of the two injectant fluids.

Table 1 Critical properties of the injectant fluids taken from NIST database (Lemmon et al. 2013)

The choice of the injectant fluids had to fulfil several criteria. Firstly, it was decided to use single-component injectant fluids to avoid additional complexity in the description of the thermal properties. Secondly, one alkane injectant was desired as a typical component of gasoline fuel. For alkanes, thermal decomposition (’cracking’) into lower order hydrocarbons is a general concern in the heating process. This may occur prior to $T_c$ for alkanes longer than 10 C-atoms (Smith et al. 1987). On the other hand, the critical pressure increases with decreasing chain length of the alkane. $\hbox {C}_{6}\hbox {H}_{14}$, hence, represents a good compromise for laboratory tests at near- and supercritical conditions as it possesses a comparably low $p_c$ and $T_c$ (Baab et al. 2017). Furthermore, Isbarn et al. (1981) showed that cracking is negligible for $\hbox {C}_{6}\hbox {H}_{14}$ for the selected temperature range which, therefore, justifies the single-component constraint.

Fig. 1

p, T-phase diagrams for $\hbox {C}_{6}\hbox {H}_{14}$ and FK illustrating reservoir, nozzle exit, and post-shock conditions

In addition, we performed injection experiments with FK at similar conditions with respect to the fluid’s critical properties. As the critical point of $\hbox {C}_{6}\hbox {H}_{14}$ and FK is different, this leads to significantly different reservoir/chamber conditions. For FK, this allows nozzle pressure ratios two orders of magnitude below that for $\hbox {C}_{6}\hbox {H}_{14}$. The thermodynamic similarities become apparent by comparison of the expansion process and the vapor-liquid saturation lines illustrated in $p,T-$ phase diagrams in Fig.1. The data for saturation line (solid), isopycnic lines (dashed), and critical point were taken from the NIST database (Lemmon et al. 2013).

The expansion process starts at the reservoir conditions labelled with index inj. Looking at the $p,T-$ phase diagram, the reservoir conditions are left of the Widom line, which separates the phase space into a region of liquid- and gas-like properties (Gorelli et al. 2006). Hence, a fluid with liquid-like density, but considerable compressibility expands within the nozzle. During the relaxation process, the fluid transforms from a high-density fluid with liquid-like properties towards a gas-like fluid of significantly lower density. The expansion process may be separated into parts, namely the expansion within the nozzle and the relaxation to ambient pressure downstream of the nozzle exit.

For the first part, we estimated the nozzle exit conditions with a one-dimensional code that assumes isentropic flow through the nozzle as detailed in Baab et al. (2014). The nozzle exit conditions are indicated with e. In case of underexpanded jets, the flow chokes within the nozzle and is discharged with sonic velocity (Anderson 1990). This leads to further expansion downstream of the nozzle exit and the formation of a shock system within a distance of a few nozzle diameters, as shown in Fig. 2. This barrel-shaped shock system prevents the entrainment of $\hbox {N}_{2}$ (Harstad and Bellan 2006), which allows for a single-component treatment of the flow up of the normal shock (Mach disk). For the present injection conditions, it can be assumed, furthermore, that the post-shock (index PS) pressure behind the Mach disk is equal to the chamber pressure $p_{\rm {ch}}$ and that the immediate post-shock temperature is approximately equal to $T_{{\rm inj}}$ (Harstad and Bellan 2006; Ewan and Moodie 1986; Birch et al. 1987).

Fig. 2

Schematic illustration of an highly underexpanded jet and its shock/expansion system

In general, the expansion process is characterized by real gas effects due to the crossing of the region of transition from liquid to gas-like properties. To illustrate the implications regarding the thermodynamic fluid properties, the ratio of specific heats $\gamma$ is plotted over the static pressure during a virtual expansion process from reservoir to chamber pressure in Fig.3. Here, highly non-linear behavior of $\gamma$ can be observed with a distinct maximum at the Widom line, which marks the transition in the thermodynamic behavior. Likewise, it is seen that the extent of non-ideal behavior is quite sensitive to the individual injection conditions used.

Fig. 3

Evolution of the ratio of specific heats $\gamma$ in the expansion process: a $\hbox {C}_{6}\hbox {H}_{14}$; b FK and $\hbox {C}_{2}\hbox {H}_{4}$

Table 2 Overview of the experimental conditions for the investigated injections

For comparison, the $\gamma$ evolution for the injection conditions of Wu et al. (1999) is included in the diagram. Their data set comprises supercritical ethylene injections $\hbox {C}_{2}\hbox {H}_{4}$ into low-pressure $\hbox {N}_{2}$ and represents a rare example of quantitative data for such conditions. Despite the fact that similar injection conditions with respect to the critical properties were used, it can be seen that a nearly ideal expansion is given in their experiments as the Widom line is not crossed in the expansion process. Consequently, real gas effects may be negligible for the presented $\hbox {C}_{2}\hbox {H}_{4}$ experiments in contrast to the present configurations. This demonstrates that a detailed analysis of the thermodynamic regime for the expansion is mandatory to characterize the injection conditions, especially in terms of non-ideal behavior. The data presented here serve as a validation basis for CFD tools that are capable of modelling real gas effects of expanding flows, particularly relevant for the simulation of underexpanded jets resulting from supercritical reservoir conditions. The experimental conditions covered in this study are summarized in Table 2.

3 Experimental facility and measurement technique

3.1 Test chamber and injection system

The jet experiments were performed in a cylindrical constant-volume chamber. The chamber design and experimental strategy are the same as in Baab et al. (2016). Chamber pressure and temperature are measured with a piezoresistive pressure sensor (Keller PA-21Y) and two K-type thermocouples, respectively.

The injection system is integrated into the front side end wall, so that the axis of injector nozzle and cylinder coincide. All $\hbox {C}_{6}\hbox {H}_{14}$ injections use a classical common rail system providing injection pressures in the order of hundreds of bars. For the low injection pressures used for the FK, a custom-made injection system is used consisting of a sealed metal container that is pressurized externally with nitrogen. The injector is based on a magnetic-valve type commercially sold by Robert Bosch GmbH fitted with a costume-made straight-hole nozzle with a diameter of $D=0.236\,\hbox {mm}$ and length of $L=1\,\hbox {mm}$ (i.e. $L/D\approx 4.2$). Two temperature-controlled heater cartridges surround the injector body and tip to heat the fluid to the desired injection temperature. The temperature calibration of the injection system has been performed in Stotz (2011) and was verified prior to this campaign. The uncertainty of injection temperature is considered to be within $\pm 2$ K.

3.2 Laser-induced thermal acoustics (LITA)

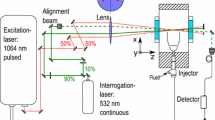
Laser-induced thermal acoustics (LITA), or more generally referred to as laser-induced gratings (LIGS), is discussed to more detail in the literature: Baab et al. (2016) with respect to its application for fuel jets or, for instance (Kiefer and Ewart 2011) for a full treatment of the theory. The discussion of underlying principles shall, therefore, be limited to the following brief outline. Two beams of a short-pulse laser source (excitation laser) are crossed to modulate the density of the test medium within the measurement volume. The resulting spatially periodic perturbation with fringe spacing $\varLambda$ scatters light of a third input wave originating from a second laser source (interrogation laser) into the coherent LITA signal beam, the temporal evolution of which is a function of the gas properties. In this case, the LITA signal is observed as damped oscillation with frequency $\varOmega _0$, which is proportional to the local speed of sound in the test medium. It is crucial to realize that the speed of sound is directly obtained from signal frequency involving only a proportionality constant (namely the grating spacing). The speed of sound is, therefore, measured without the use of an equation of state or other thermodynamic modelling assumptions. This makes the technique particular feasible for the use in fluids with non-ideal thermodynamic behavior for which the development of accurate EoS is a difficult task.

3.2.1 Optical setup

The optical arrangement is illustrated in Fig. 4. Note again that it is adapted from earlier versions of the setup described in Förster et al. (2015) and Baab et al. (2016). The description here is, therefore, limited to the essentials like the wavelengths of the excitation ($\lambda =1064\,\hbox {nm}$) and interrogation beams ($\lambda =532\,\hbox {nm}$). All beams are focused by a lens with a focal length of $700\,\hbox {mm}$, which results in a $3^{\circ }$ crossing angle of the excitation beams. This results in an ellipsoidally shaped interaction region of the excitation beams with a diameter of approximately $200\,\upmu \hbox {m}$ and less than 8 mm in length. Note that this represents the worst-case approximation of the measurement volume as the interrogation beam only partially overlaps the excited region. The same configuration was used in Baab et al. (2016) that allowed resolution of the radial profiles of the jets whose characteristic dimensions typically comprise several nozzle diameters ($\text{ D }=236\,\upmu \hbox {m}$). To ensure that the optical alignment for this study has the same accuracy in probing the centerline as the previous study, the same alignment approach is used, i.e. the visualization of the laser beam paths via a CCD chip.

Fig. 4

Experimental setup of LITA measurements in fuel jets

3.2.2 Post-processing

The LITA signal is characterized by a frequency proportional to speed of sound in the medium. The corresponding constant of proportionality is found in a calibration experiment using a system with known thermodynamic properties. The calibration procedure is identical to the one in Förster et al. (2015), where the effect of uncertainties from the calibration is found to be within 1.3%. One of the important features of LITA is that this characteristic frequency is also found if the LITA is heavily deteriorated by scattering events caused for instance by inhomogeneous density fields along the beam path lengths and turbulence. This advantage makes LITA especially desirable for the present application. Two post-processing algorithms are used here. For chamber pressures at 0.2 MPa and below, the signal frequency is derived from an individual detection of the oscillation periods. This approach is found superior to an FFT due to the small number of signal oscillations found under these conditions. It is based on determining the intersection of tangents on rising and falling edge defined by a gradient criterion and was validated in Baab et al. (2016). For all chamber pressures above 0.2 MPa, LITA signals were post-processed using a FFT. Although both approaches yield identical results, the FFT was selected as being the more conventional analysis tool.

While the speed of sound is directly measured by extracting the signal frequency, it is possible to derive further fluid properties through a thermodynamic interpretation of this parameter. For a mixture of gases in local thermodynamic equilibrium, the speed of sound $a_{\mathrm{mix}}$ is generally a function of species concentration, temperature and pressure, that is

$$\begin{aligned} {a}_{\mathrm{mix}}={a}_{\mathrm{mix}}(c_{\mathrm{mix}},T,p), \end{aligned}$$

(1)

where $c_{\mathrm{mix}}$ contains the mass fractions of the mixing components. Hence, for an isobaric mixing process at known pressure, ${a}_{\mathrm{mix}}$ is defined by the local mixture composition and temperature. On the basis of a measured speed of sound ${a}_{\mathrm{meas}}$, either T can be determined for known $c_{\mathrm{mix}}$ or vice versa. In its simplest form, this relation may be given by the ideal gas law, ${a}_{\mathrm{mix}}(c_{\mathrm{mix}},T,p)=\sqrt{{\gamma _{\mathrm{mix}}}{R_{\mathrm{mix}}}T}$ with ${\gamma _{\mathrm{mix}}}$ as the ratio of specific heats and ${R_{mix}}$ the specific gas constant for the ideal gas mixture.

However, if one or more mixture components cannot be approximated as ideal gases, this simple relation for ${a}_{\mathrm{mix}}$ is not valid. Especially for fluids close to their saturation state (e.g., dew-point line) and at high pressures (particularly near the critical pressure), incorporation of real fluid behavior is mandatory. High-order equations of state (EoS) in combination with non-linear mixing rules are then necessary to calculate thermodynamic properties. Considering the thermodynamic regimes for the presented injection case as discussed in Sect. 2, these effects have to be considered here. Again, this approach was developed in Baab et al. (2016) and the inclined reader is referred to this publication for a more rigorous treatment of the underlying thermodynamics.

To provide a brief description of the principle, it can be said that the ambiguity of $a_{\mathrm{meas}}$ with respect to $c_{\mathrm{mix}}$ and T is overcome by assuming an adiabatic mixing of injectant and ambient gas. This is justified as the mixing process is dominated by advection, while diffusion plays a negligible role in the mass and energy transport.

The specific enthalpy of a real mixture consists of the enthalpy of the ideal mixing process as well as an excess contribution from non-ideal mixing process. Here, $h_{\mathrm{mix}}(c_{\mathrm{mix}},T_{\mathrm{mix}},p_{\rm {ch}})$ of the real mixture at an adiabatic mixing temperature $T_{\mathrm{mix}}$ can then be expressed as follows:

$$\begin{aligned} \begin{aligned}&h_{\mathrm{mix}}(c_{\mathrm{mix}} ,T_{\mathrm{mix}},p_{\mathrm{ch}}) = \dots \\&\quad \dots h_{\mathrm{excess}}(c_{\mathrm{mix}},T_{\mathrm{mix}}, p_{\mathrm{ch}}) + h_{id}(c_{\mathrm{mix}},T_{\mathrm{mix}},p_{\rm {ch}}). \end{aligned} \end{aligned}$$

(2)

Here, $h_{\mathrm{id}}$ is the specific enthalpy that originates from ideal mixing of fluid and $\hbox {N}_{2}$, while $h_{\mathrm{excess}}$ accounts for the non-ideality of the binary system. As discussed in Baab et al. (2016), the pressure and temperature of both the injected fluid and the environment are known prior to mixing. In the calculation procedure, $a_{\mathrm{mix}}$ and all $h_i$ (including the excess contribution) have been tabulated from REFPROP for the relevant t and p range. An iterative scheme optimizes for $c_{\mathrm{mix}}$ and $T_{\mathrm{mix}}$, so that

$$\begin{aligned} a_{\mathrm{mix}}(c_{\mathrm{mix}},T_{\mathrm{mix}},p_{\rm {ch}}) {\mathop {=}\limits ^{!}} a_{\mathrm{meas}}, \end{aligned}$$

(3)

while at the same time

$$\begin{aligned} \begin{aligned}& h_{\text{mix}}(c_{\text{mix}},T_{\text{mix}},p_{\text{ch}}) - h_{\text{excess}}(c_{\text{mix}},T_{\text{mix}},p_{\text{ch}}) {\mathop {=}\limits ^{!}} \dots \\& \quad \dots c_{\text{fluid}} h_{\text{fluid}}(T_{\text{ps}},p_{\text{ch}}) + (1-c_{\text{fluid}}) h_{\text{N}{_{2}}}(T_{\rm {ch}},p_{\rm {ch}}). \end{aligned} \end{aligned}$$

(4)

Although this approach yields an approximation of $c_{\mathrm{mix}}$ and $T_{\mathrm{mix}}$, it should be stressed that it is possible to account for real fluid behavior using the NIST database. Hence, the developed approach is generally valid for non-ideal mixing provided that energy transfer through diffusion (of heat or mass) within the mixing zone is negligible. The general relation between $a_{\mathrm{mix}}$, $T_{\mathrm{mix}}$ and $c_{\mathrm{mix}}$ is illustrated in Fig. 5. For $\hbox {C}_{6}\hbox {H}_{14}$, this relationship is non-monotonic for small concentrations. However, all measured speeds of sound were found below $350\,\hbox {m}\,\hbox {s}^{-1}$, which assures a distinct determination. For FK, on the other hand, this ambiguity does not exist at the investigated conditions.

Fig. 5

Speed of sound for adiabatic mixing of n-hexane and FK with $\hbox {N}_{2}$ at $p_{\rm {ch}}=0.5\,\hbox {MPa}$: $c_{fluid}$ refers to the concentration of $\hbox {C}_{6}\hbox {H}_{14}$ and FK, respectively

4 Results

The results are presented in two parts. Experimental speed of sound data sets is provided at different positions and varying injection temperature. Based on these measurements, centerline concentrations are estimated using an adiabatic mixing model based on non-ideal fluid properties.

4.1 Experimental speed of sound data

Table 3 Speed of sound of pure n-hexane, FK and $\hbox {N}_{2}$ at relevant temperatures and constant pressure of $p_{\rm {ch}}=0.5\,\hbox {MPa}$

Fig. 6

$\hbox {C}_{6}\hbox {H}_{14}$ injections with nozzle pressure ratio of 150 and 600

In a first step, the range of the speed of sound values for the particular binary system (fluid/gas) are evaluated. Under the assumption of a fully adiabatic mixing process of injectant and ambient gas, this range is determined by the pure injectant at $T_{\mathrm{inj}}$ and $\hbox {N}_{2}$ at $T_{\mathrm{ch}}$. The pressure within the far-field mixing domain is equal to the corresponding chamber pressure $p_{\mathrm{ch}}$ as the injected jet has fully adapted at this stage. However, variations in speed of sound due to the different chamber pressures are small and so this first assessment is done as an example for $p_{\mathrm{ch}}=0.5\,\hbox {MPa}$ as for Fig. 5. Table 3 lists the relevant speed of sound data for both injectants and the ambient gas. All data are taken from NIST database (Lemmon et al. 2013). It is evident that the initial speed of the sound of the pure injectant defines the possible range for the mixture and, ultimately, the sensitivity of $a_{\mathrm{mix}}$ towards the mixture properties. In the case of $\hbox {C}_{6}\hbox {H}_{14}$, this spread is beyond $100\,\hbox {m}\,\hbox {s}^{-1}$, which proved to be sufficient in preceding studies (Baab et al. 2016). For the FK/$\hbox {N}_{2}$, this spread increases to $240\,\hbox {m}\,\hbox {s}^{-1}$ as a result of the very low speed of sound of FK, which makes the fluid an interesting choice both from scientific point of view and the diagnostic technique itself.

Fig. 7

$\hbox {C}_{6}\hbox {H}_{14}$: influence of different chamber pressures

Figure 6 shows centerline measurements for two different NPRs at varying $T_{\mathrm{inj}}$. Here, and for all following figures, error bars represent the standard error of the mean (i.e. one sample standard deviation divided by the square root of the sample size). As detailed in Baab et al. (2016), an approximately linear relationship was found between $a_{\mathrm{meas}}$ and $T_{\mathrm{inj}}$ for fixed x/D. The data in Fig. 6 show that this trend is preserved even when the expansion ratio is four times larger (600 instead of 150). Likewise, the difference in measured speed of sound for the different NPR is approximately constant, i.e. same gradient, for all injection temperatures. Note that the existing data set in Baab et al. (2016) only contains one NPR of 150 and the axial range is limited to $x/D=55, 80$, and 110. Because a deviation from this trend is expected for a position further downstream of the injection point, Fig. 7 provides $a_{\mathrm{meas}}$ in the far-field at $x/D=173$ for various NPRs. It is seen that the linear slope is maintained for NPRs down to 60, but deviates for lower NPRs, i.e. $\hbox {NPR}=30$.

This behavior is most likely explained by the lower injectant concentrations due to the lower NPR and the resulting higher entrainment of $\hbox {N}_{2}$. In addition, the low injectant concentrations approach the non-linear region in the speed of sound dependence, as shown in Fig. 5. Hence, for the following experiments, the measurement position was set closer to the nozzle again. Furthermore, it is seen that as fuel concentration reduces, the measured speed of sound approaches the value of nitrogen at chamber conditions. To vary the nozzle pressure ratio further, an injectant with lower initial speed of sound is required, so that low concentrations result in a significant change of $a_{\mathrm{mix}}$ compared to nitrogen.

Following these considerations, we used FK as an injectant for the very low NPR. Figure 8 shows the obtained $a_{\mathrm{meas}}$ for FK at $T_{\mathrm{inj}}=500\,\hbox {K}$ for different x/D along with the data acquired for $\hbox {C}_{6}\hbox {H}_{14}$ in Baab et al. (2016). However, instead of varying $T_{{\rm inj}}$, Fig. 8 focuses on the axial evolution for different NPRs. Similar trends as previously for both the injection temperature and axial position are found for the much lower NPRs. Given that NPRs as low as 4 are realized for the FK jets, the jets approach the limit for underexpansion and, hence, conclude the highly underexpanded flow regime.

Fig. 8

Comparison $\hbox {C}_{6}\hbox {H}_{14}$ and FK at different axial positions x/D

Fig. 9

Comparison $\hbox {C}_{6}\hbox {H}_{14}$ and FK for varying nozzle pressure ratios

Figure 9 shows the evolution of $a_{\mathrm{meas}}$ along the centerline for decreasing NPR at $x/D=110$. For the $\hbox {C}_{6}\hbox {H}_{14}$ jets, it is seen that a change in injection temperature results in an approximately constant offset of the linear trend, while, for FK, the gradient of the linear slope changes. This is due to the lower $a_{FK}(T_{\mathrm{inj}},p_{\mathrm{ch}})$. In addition to the graphic illustrations, Table 4 in the appendix provides a detailed listing of the acquired experimental data. Furthermore, radial profiles at fixed axial positions were published in Baab et al. (2016) for $\hbox {C}_{6}\hbox {H}_{14}$ at $\hbox {NPR}=150$.

4.2 Mixing characterization

The adiabatic mixing approach was used for all conditions in Table 2. Figure 10 summarizes the values of the centerline concentrations obtained in this work. The results are plotted over a non-dimensional parameter that originates from a similarity analysis initially proposed by Chen and Rodi (1980) and used in Baab et al. (2016) to describe the axial concentration decay for momentum-controlled mixing. The dotted line in Fig. 10 represent this similarity parameter given by the following:

$$\begin{aligned} c_{cl} = A \left( \frac{\rho _e}{\rho _{\mathrm{ch}}}\right) ^{0.5}\left( \frac{x}{D}\right) ^{-1}. \end{aligned}$$

(5)

Here, A is an empirical scaling constant (set to $A=5.4$), $\rho _e$ the injectant density at the nozzle exit plane, and $\rho _{\rm {ch}}$ the ambient gas density. While this equation was successful in condensing experimental concentration data for the n-hexane jet injected into nitrogen at $p_{\rm {ch}}=0.2\,\hbox {MPa}$ as well as for the data published by Wu et al. (1999), noticeable deviations are found for the present data that feature higher chamber pressures. This was initially surprising as Molkov (2012) used Eq. 5 with $A=5.4$ as well to condense experimental concentration data for both expanded and underexpanded, non-ideal hydrogen jets at high pressures – and, hence, for a wide range of expansion ratios and other experimental conditions (i.e., pressure ratio, nozzle diameter, and axial distance).

Fig. 10

Similarity analysis of $c_{cl}$ for $\hbox {C}_{6}\hbox {H}_{14}$, FK, and $\hbox {C}_{2}\hbox {H}_{4}$ injections using the approach in Baab et al. (2016)

However, it is explained due to the fact that experimental data featured in Molkov (2012) focus on safety aspects of hydrogen storage. Therefore, it exclusively considers leakage of high-pressure storage and, hence, an expansion to ambient pressure. While a chamber pressure of $p_{\mathrm{ch}}=0.2\,\hbox {MPa}$, as used for our previous experiments published in Baab et al. (2016) as well as for the work of Wu et al. (1999), seems acceptably close to this value, higher chamber pressures of up to $1.5\,\hbox {MPa}$ are not described accurately. Looking at Eq. 5 again, it is seen that the correlation includes only a relative factor for the injectant/chamber conditions, but makes no statement about the absolute level of the nozzle flow. Therefore, we chose to include a non-dimensional parameter that relates to the nozzle exit conditions, namely the exit Reynolds number $Re_e=\frac{\rho _e v_e D}{\eta _e}$. This leads to an empirical fitting function in the form:

$$\begin{aligned} \frac{1}{c_{cl}} = \left( \frac{x}{D}\right) \left( A \left( \frac{\rho _e}{\rho _{\rm {ch}}}\right) ^{n} \left( \frac{Re_e}{10^5}\right) ^{m}\right) ^{-1}+C. \end{aligned}$$

(6)

By fitting all data points, included those published in Baab et al. (2016) and Wu et al. (1999), a new empirical correlation is found for the constants $A=75$, $n=0.6$, $m=-1.2$ and $C=1$. As seen in Fig. 11, this relationship provides a better representation of the complete data set. Note that these constants, in this study and in Molkov (2012), are empirical, obtained by the best fit to the data, and do not represent a physical property. At this stage, it is, hence, not applicable for the entirety of possible injection conditions but optimized for the data in the present and cited studies.

Fig. 11

Empirical fit proposed on basis of the experimental data to include both exit density ratio and Reynolds number

5 Conclusions

In this study, we investigated the mixing characteristics of underexpanded fluid jets with supercritical reservoir conditions discharged into a cold nitrogen atmosphere at subcritical pressure (with respect to the injectant). By applying laser-induced thermal acoustics, a technique previously suggested and successfully demonstrated for the present flow fields, a quantitative speed of sound data set is generated for a wide range of experimental conditions. The need for such experimental database is frequently stated in the literature and the main intention of this paper is to present reference test cases for evaluating numerical tools. To our knowledge, it is the first study to provide quantitative data for validation to this extent.

In this study, two injectants, different in respect to their critical properties, viz., n-hexane and Novec 649, are studied for nozzle pressure ratios from 4 to 600, hence covering a wide range from highly to extremely highly underexpanded jets. Simultaneously, the injection temperature is varied to resolve characteristic trends in the resulting speed of sound distribution along different axial positions on the centerline.

In addition to the measured speed of sound, an adiabatic mixing model based on non-ideal fluid properties is used to estimate local mixture compositions. All concentration data are expressed by an empirical fit based on the injectant properties at the nozzle exit. For the presented data, it states that the far-field mixing is well characterized using the calculated exit density, the injected mass flux, and the density of the gas atmosphere in which the jet is injected into. Hence, the proposed fit allows to estimate the mixing characteristics of underexpanded fluid jets without the requirement to characterize the complex thermodynamic process of the expansion from the nozzle exit to chamber conditions.

Appendix

In addition to Figs. 6, 7, 8, 9, 10, 11, all data are summarized in Table 4 for easy access. Parameters measured in the individual experiments include $p_{\mathrm{inj}}$, $p_{\mathrm{ch}}$, $T_{\mathrm{ch}}$, x/D, and $a_{\mathrm{meas}}$. $T_{{\rm inj}}$ is based on measured data, but ultimately results from the calibration procedure described in Stotz (2011).

The parameter $p_{e}$ and $T_{e}$ are calculated based on the isentropic nozzle flow approach detailed in Baab et al. (2014), $c_{\mathrm{ad}}$ using $a_{\mathrm{meas}}$ and the adiabatic mixing model. Both $a_{\mathrm{meas}}$ and $c_{\mathrm{ad}}$ are stated plus/minus the standard error of the mean.

All data are obtained at the centerline. Note that radial profiles for $\hbox {C}_{6}\hbox {H}_{14}$ and $\hbox {NPR}=150$ are published in Baab et al. (2016).

Table 4 Summary of the experimental data set: all measurements refer to $y/D=0$