1 Introduction

Cochlear implants are state-of-the-art neuro-implants for profound hearing loss that stimulate the spiral ganglion of the auditory nerve electrically. While speech intelligibility in quiet environments is sufficient for most patients, there are strong deficits concerning speech perception in noise and tonal languages, as the frequency resolution is mainly reduced compared to normal human hearing.

Different alternatives, such as optical stimulation methods, are being investigated to increase frequency selectivity. There are also other approaches to optical stimulation such as infrared stimulation and optogenetics. While the infrared method researched by, e. g., the group of Richter uses the thermal effect for stimulation [1, 2], in our previous study, we applied the nonlinear optoacoustic effect [3], which utilizes the shockwave emission during optical breakdown and accompanying generation of cavitation bubbles in transparent media [4,5,6,7,8,9,10,11]. This mechanism has the main advantage that the thermal influence on the surrounding medium is negligible and the shorter thermal time constant allows for a higher maximum repetition rate. By high-repetition-rate laser pulse trains, tones can be generated, e.g. in the cochlear fluid, and detected by the hair cells that convert them into auditory nerve signals, via the same principle as normal hearing.

In our experiments, we exploit the nonlinear optoacoustic effect—the generation of cavitation bubble as the result of a cascade of free electrons within the focus of a short laser pulse—to trigger a plasma with the accompanying shockwave as an acoustic event. The concatenation of laser pulses was used by our group to generate tones covering the entire human hearing range [3]. In this previous work, we used a laser focused on a viscous gel. An optical breakdown with an accompanying short pressure event was induced by the high energy density within the laser focus deposited by each laser pulse. For frequencies below 500 Hz, a pulse density modulation was applied, resulting in modulation frequency fundamentals of the laser-generated tone.

This study investigates the underlying bubble dynamics with both a computational model and additional experiments with an increased temporal resolution. To achieve this, we simulated the cavitation bubble dynamics with a finite volume method. Additionally, we measured the exact time development using a fast needle hydrophone with a time resolution of approx. 20 MHz, sufficient for measurements of cavitation bubble pressure peaks with typical widths < 1 µs [12, 13].

The simulation was developed with a finite volume method in OpenFOAM, an open-source computational fluid dynamics toolbox [14]. The computational model is based on the model by Koch, that applies the Finite Volume method for spatial discretization and the Volume of Fluid method for the two phases of gas inside the bubble and liquid surrounding the bubble [15]. A flexible design of the geometry is possible with OpenFOAM and shock wave phenomena can be modelled as well as the radius development of the bubble.

Here, we extend this model for the investigation of the effects of viscosity in reference to our earlier study. Additionally, we investigated the influence of a confined volume such as the cochlea to assess the dynamics induced by a hearing aid based on nonlinear optoacoustic stimulation. With a diameter of approx. 1 mm, it is expected that the liquid-bone boundaries in the cochlea lead to several reflections of the acoustic waves. As a pre-step, we tested a geometry with one rigid boundary near the laser focus, both in our computational model and in experiments.

2 Methods

2.1 Experiment

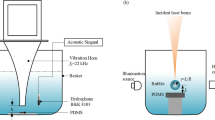
The first experimental setup is similar to our previous study [3]. A nanosecond pulsed laser (HELIOS 1064-5-50, Coherent, Inc.) with a wavelength of 1064 nm, a pulse duration of 0.7 ns, and a pulse energy of 20 μJ was used. The laser power was controlled using a half-wave plate (WPH05M-1064, Thorlabs) and a polarizing beam splitter (PBS12-1064, Thorlabs). Lenses served to adjust the beam diameter to the focusing objective (Mitutoyo Plan Apo SL infinity corrected 20×, 378-810-3, Edmund Optics) with a numerical aperture (NA) of 0.28. The laser focus was placed in a water container (4 × 4 × 6 cm3). On the optical window, PNC 400 gel with a concentration between 3 and 20 g/l was placed inside the container, such that the laser focus was within the gel (cf. Fig. 1b). To investigate the bubble dynamics in the first series of experiments, we applied single laser pulses. The gel was manufactured by mixing the respective amount of PNC 400 powder with distilled water and centrifugation afterwards (for details see [3]). The gel layer in the fiber-based setup was quasi-cylindrically shaped and approx. 3–4 mm thick and approx. 2–3 mm in diameter. The gel has a density that deviates from the density of water by less than 5%. Hence, the acoustic impedance difference is negligible.

Fig. 1
figure 1

a Experimental setup with half-wave plate and polarizing beam splitter (PBS) to control the laser power, and two lenses (f1, f2) to adjust the beam diameter to the objective, which focuses the laser into the water container with gel (yellow) around the laser focus. The pressure is measured with a needle hydrophone (H), which is read out by a high-speed oscilloscope (OSC). b Setup with fiber end, two ball lenses (BL) glued into a polymer ferrule

Full size image

Pressure measurements were conducted with a needle hydrophone (diameter 1 mm, NH1000, Precision Acoustics) with a maximum time resolution of 20 MHz, which allows for sufficiently time-resolved investigation of the bubble dynamics. However, the uncertainty of the measured pressure is between 9 and 18%, depending on the frequency [16]. A high-speed oscilloscope (Rohde & Schwarz RTB2004) with a 1 GHz sampling rate served to read out the hydrophone signal.

In the experiments, different gel concentrations—equivalent to a variation of the viscosity—were applied and the change in the pressure transients was investigated, focusing on a change in the amplitude and the duration between the expansion and the collapse. Additionally, the influence of the distance to the nearest wall of the water container was measured to mimic a future application in the confined geometry of the human cochlea. Additionally, an experimental setup for a minimum bubble to boundary distance and for future application in the inner ear was built. The laser was delivered by a fiber setup (step-index multimode fiber, FP1000ERT, NA = 0.5, core diameter 1 mm, Thorlabs) with the same laser as in [3]. At the fiber end, two ball lenses (43-709, Lens ball, Edmund optics, diameter 1.5 mm, refractive index 1.517) glued into a plastic ferrule created the laser focus. This focusing setup was inspired by Yang et al., where the same fiber diameter and lens diameters were used for imaging [17].

2.2 Computational model

Both the influence of the viscosity and of the geometry were simulated with a numerical model for cavitation dynamics in foam-extend, an extension of OpenFOAM, with the solver compressibleInterFoam, based on the model by Koch, who already applied it for laser-induced bubble dynamics in water [15]. We extended this model for the application with viscous media surrounding the bubble as well as for the confined volume. To this end, we chose different matrix solvers than Koch.

The basic assumption of the model is that the cavitation bubble is an oscillating gas bubble with an expansion phase and several collapses until the temperature of the bubble equals the surrounding liquid [9, 18]. For further details on the assumptions of the model, see [15].

The main equations that are used in OpenFOAM are the equations of state and the equations of motion. The equations of state are the Tait and the Nobel Abel equations, for water and gas, respectively. The equations of motion consist in our case of a continuous, moving fluid that is locally in thermodynamic equilibrium, of five distributional quantities: three velocity components U(r, t) and two thermodynamic variables—here: pressure p(r, t) and density ρ(r, t). Hence, five equations are necessary to solve the system. In this application, as the model uses a Volume of Fluid method, there is a sixth parameter necessary to distinguish between the gas inside the bubble and the liquid in the surrounding medium, which is α [15].

In this model, we applied the Navier–Stokes-equation with the tensor T for the viscous tension, \(\sigma\) for the surface tension, \(\kappa\) for the double of the average curvature of the surface, S for the contact area between the bubble and the surrounding liquid, the viscosity µ, and \(\otimes\) for the dyadic product [15, 19]:

$$\frac{{\partial \left( {\rho U} \right)}}{\partial t} + \nabla \cdot \left( {\rho U \otimes U} \right) = - \nabla p + \nabla \cdot T + \mathop \smallint \limits_{S\left( t \right)} \sigma \kappa (x^{\prime})\hat{n}\left( {x^{\prime}} \right) \delta \left( {x - x^{\prime}} \right){\text{d}}S^{\prime},$$
(1)

with

$$T = \mu (\nabla U + \left( {\nabla U} \right)^{{\text{T}}} - \frac{2}{3}\left( {\nabla \cdot U} \right) {\mathbb{I}}).$$
(2)

The Tait equation of state describes the thermodynamics of a cavitation bubble in water-like media:

$$p\left( \rho \right) = \left( {p_{\infty } + B} \right)\left( {\frac{\rho }{{\rho_{\infty } }}} \right)^{{n_{{\text{T}}} }} - B,$$
(3)

with \(p_{\infty }\) as the atmosphere pressure, \(\rho_{\infty }\) as the equilibrium density, \(B = 304.6\;{\text{MPa}}\) as the Tait pressure and \(n_{{\text{T}}} = 7.15\) as the Tait exponent.

For the gas inside the bubble, the Nobel Abel equation of state is used [15, 20]:

$$R_{{\text{spec }}} T = p \left( {\frac{1}{\rho } - \frac{\beta }{{\rho_{\infty } }}} \right),$$
(4)

wherein \(R_{{\text{spec }}}\) describes the specific gas constant and \(\beta\) the co-volume.

The maximum bubble radius Rmax is calculated for water as the surrounding medium pressure is dependent on the half-time interval \(t_{{\text{c}}}\) between pressure waves of the expansion and the first collapse by [21]:

$$R_{{{\text{max}}}} = 1.09 \sqrt {\frac{{p_{0} - p_{{\text{v}}} }}{{\rho_{{\text{l}}} }}} t_{{\text{c}}} ,$$
(5)

with p0 = 1 bar; \(\rho_{{\text{l}}}\) = 1 × 103 kg/m3 (for water at 20 °C), vapor pressure pv = 0.0233 bar. Due to the neglection of viscosity influences in this equation, it cannot be applied for the viscous gel.

In addition, a parameter α was applied to distinguish between the gas and liquid phase, such that, due to the neglection of mass transfer between the phases, the following continuity equation was applied [15]:

$$\frac{{\partial \left( {\alpha_{i} \varrho_{i} } \right)}}{\partial t} + \nabla \cdot \left( {\alpha_{i} \varrho_{i} U} \right) = 0.$$
(6)

The maximum bubble radius was calculated from Eq. (2) with the experimentally measured time interval \(t_{{\text{c}}}\) = 11 µs in water (chapter 3A) with a result of \(R_{\max } =\) 118 µm. However, Eq. (2) is only valid for inviscid media and hence was not used for the gel applied in the experiments.

To compare the experiment and the model, the time distance between the expansion and the first collapse tcis the first important parameter [22]. In our model, we applied the energy-deposit case, which includes both the expansion phase after the laser energy is deposited within the medium and the collapses that follow later. However, the simplification of the model does not allow to start immediately at energy deposition. Hence, we chose to perform the simulation starting with an initial bubble radius of 20% of the maximum bubble radius in agreement with [6].

The most important parameters of the model are the excess pressure pexc that is responsible for driving the expansion but does directly not correspond to the pressure value emitted by the bubble, the maximum bubble radius Rmax, the equilibrium radius Rn (i.e., the final radius after oscillations have ceased, for \(t \to \infty\)), and the characteristic parameters of the surrounding medium, i.e. viscosity, density, and vapor pressure. The corresponding equilibrium pressure pn is calculated from the equilibrium radius Rn by [15]:

$$p_{n} = p_{\infty } + \frac{2\sigma }{{R_{n} }}$$
(7)
$$p_{0} = p_{n} \left( {\frac{{R_{n}^{3} - \beta R_{n}^{3} }}{{R^{3} - \beta R_{n}^{3} }}} \right)^{\gamma } ,$$
(8)

where σ is the surface tension, γ = 1.4 is the adiabatic exponent with the value for air, and p∞ = 101,315 Pa. The parameter β describes the co-volume and is given by Koch as [15]:

$$\beta = \frac{{p_{n} b_{{{\text{Van}}}} }}{{R_{{{\text{general}}}} T_{{{\text{ref}}}} + p_{n} b_{{{\text{Van}}}} }},$$
(9)

where bvan is the Van-der-Waals-constant, Rgeneral is the general gas constant (in J/(mol K)), Tref is the reference temperature (in K).

The initial low pressure requires an adjusted initial density within the bubble as well. Since there is no condensation or evaporation in the model, the chosen density determines the bubble mass for the model and is calculated by [15]:

$$\rho_{n} = \frac{{p_{n} }}{{\left( {R_{{{\text{spec}}}} T_{{{\text{ref}}}} \left( {1 - \beta } \right)} \right)}}$$
(10)
$$\rho_{0} = \rho_{n} \left( {\frac{{R_{n} }}{{R_{0} }}} \right)^{\gamma } .$$
(11)

The expansion of the bubble requires to set a pressure source with an initial excess pressure pexc:

$$p_{{{\text{exc}}}} \left( t \right) = p_{{{\text{exc}}}} e^{ - \lambda t}$$
(12)

Hence, the expansion is driven by pexc with a rapid fall-off with a time-constant λ.

The model only allowed for a constant viscosity, independent of the frequency. The relevant frequency regime is approx. 100 kHz–10 MHz for the pressure rise and fall-off of the bubble expansion and collapse. The measured values of the shear-dependent dynamic viscosity for 1–20 min−1 were extrapolated to this regime. The dependence was strong in the regime of ca. 1–10 min−1, but weaker towards higher shear rates. In addition, the literature reports Newtonian plateaus at high shear rates [23]. The extrapolated values were converted to kinematic viscosity and applied in the simulation (cf. Table 1).

Table 1 Viscosity values: dynamic viscosity measured (from [3]) and extrapolated dynamic and kinematic viscosity at high frequencies
Full size table

2.3 Meshing

The viscosity investigation was modelled with spherical symmetry in a one-dimensional mesh. All other investigations regarded the geometry and are were modelled in axial symmetry in two dimensions (cf. Appendix for details on the meshing).

The model requires a mesh that allows for precise but also efficient calculations. The meshing was done with the utility blockMesh given by OpenFOAM with hexahedral blocks.

By choosing fitting boundary conditions and a symmetrical setup, the calculations were reduced to a lower-dimensional problem while still yielding three-dimensional result. For spherical cases, the problem can be reduced to one dimension and hence only a slice of a sphere was calculated. For the boundary case with only an axisymmetric geometry, thus two-dimensional, another mesh was applied.

The desired precision of the calculation results requires that the size of the blocks is smaller near the cavitation bubble surface. The width of the blocks has to be designed such that it grows consistently with the radial coordinate and that the resulting sum of blocks is a section of a sphere.

The boundary conditions for the simple setup of the cavitation bubble without rigid boundaries were chosen such that the opposite side faces are connected by the built-in boundary condition “wedge”. The outer face in radial direction requires setting three vector fields: the volume fraction α to distinguish between liquid and gas phase, the velocity U and the pressure field p. For the volume fraction, the “zeroGradient” boundary condition was applied, which resulted in the boundary field having the value of the internal field. As water should not flow out of the domain, the velocity boundary field is set to zero with the condition “pressureInletOutletVelocity”, which allows only for pressure-induced temporary flows. For the boundary of the pressure field, the “waveTransmissive” condition is applied, as it undermines the reflection of outgoing waves.

For the case with one rigid boundary, a two-dimensional model with only axisymmetric geometry, the inner core of the wedge was deformed by an additional parameter. The non-orthogonality and ratio of the side lengths of the cells are small, as the mesh is split up into four block sections for meshing with blockMesh, with the core section approaching a radial form outwards (cf. Fig. 8). The rigid boundary was placed at a distance of 2 × Rmax to the bubble center, at the wall orthogonal to the symmetry axis at which the bubble is mirrored, with all other boundaries remaining open as before. The corresponding boundary conditions for the rigid boundary were chosen as “zeroGradient” for alpha and the pressure and as “fixedValue” for the velocity.

For the cochlear geometry, a special mesh was designed with the cochlear approximated by a cylinder which is 22 mm long and has a radius of 1 mm, as the literature reports similar dimensions for human cochleae, but untangled and simplified by letting out the basilar membrane as the separation between scala vestibuli and scala tympani [24]. The cylinder for the cochlea model was modelled with rigid walls, while only one side is open by the “waveTransmissive” and “pressureInletOutletVelocity” boundary conditions [25]. The open top of the cylinder is placed opposite to the pressure source on the bottom, which has a distance of 1 mm to the wall. The bubble is hence located on the axis of symmetry. A grading of the mesh parallel to the axis and in the radial direction was chosen to better support the actual bubble dynamics.

3 Results of the model and experiment for viscosity variation

3.1 Spherical cavitation bubble in water

First, the experiment and simulation were conducted with the kinematic viscosity of water, i.e., 1 × 10−6 m2/s and in the objective-based setup. The experimental results shown in Fig. 2 (and analog for Figs. 3, 4a–c, 6) are single representative measurements out of ten measurements. The needle hydrophone measurement showed clearly the expansion (1), the first collapse (2), the second collapse (3), and one reflection for each of the former (R1–R3), cf. Fig. 2. The reflections occurred after ca. 3.5 µs, equivalent to ca. 5.25 mm acoustic path. With the reflection occurring at the optical window distance of ca. 3 mm, the acoustic path is expected to be ca. 6 mm, but the pressure wave has a supersonic velocity at the beginning. Hence, the measurement was in agreement with the experimental geometry.

Fig. 2
figure 2

Pressure measurement in water after inducing a cavitation bubble with a laser pulse energy of 10 µJ, measured with the needle hydrophone. a The pressure waves from the expansion (1), first and second collapse (2, 3) are visible, as well as the reflections (R). b The same measurement (black) with the simulation results (red) with an extrapolated kinematic viscosity of 1 × 10−6 m2/s for water, an excess pressure pexc = 1.31 GPa, a maximum bubble radius calculated by Eq. (2) from the tc value of the experiment to be Rmax = 118 µm and an equilibrium bubble radius Rn = 26 µm

Full size image
Fig. 3
figure 3

Experimental results for pressure transient (a–f), measured with the needle hydrophone with different gel concentrations (black) in the objective-based setup. Corresponding simulations (red) without reflective boundaries (1D spherical symmetry) with estimated kinematic viscosity (cf. Table 1)

Full size image
Fig. 4
figure 4

a–c Simulation results of the radius development for different viscosities and bubble radii (same parameters as simulation in Fig. 3); d summary of experimental results from Fig. 3 for time interval tc between expansion and collapse as a function of dynamic viscosity (cf. Table 1). Mean values (circles) from 5 measurements, error bars depict standard deviation

Full size image

The rebounds (collapses) of the bubble occurred after 22 µs and an additional 12 µs. The amplitude ratio between the expansion pressure wave and the first collapse was ca. 70% and from the first to the second collapse ca. 40%.

The simulation was conducted with a viscosity of 1 × 10−6 m2/s and a maximum bubble radius calculated by the Rayleigh equation (Eq. 5) from the experimentally measured time constant tc = 11 µs to be Rmax = 118 µm. Then, the equilibrium radius and the excess pressure were varied to fit the model pressure development to the experimentally measured pressure development. With an excess pressure pexcess = 1.31 GPa and an equilibrium bubble radius Rn = 26 µm, the experimental results for the interval between the first and second collapse were best approximated. Reflective boundaries were not included in this part of the simulation, hence no reflections occurred in this model. The distance of the probe location was chosen based on the amplitude of the maximum pressure of the expansion. The time course of the amplitudes of the expansion and the two rebounds were similar between model and experiment (cf. Fig. 2). However, the third rebound could not be measured experimentally, most probably due to the background noise, mostly caused by the needle hydrophone and its limited sensitivity. The duration between expansion and first collapse in the simulation differed by approximately 2 µs from the experiments. The main reason might be the excess pressure which was chosen to fit to the absolute amplitudes of the pressure peaks. In addition, the needle hydrophone has an uncertainty in amplitude of 9–18%. This is supported by the fact that the bubble radius reaches only 116 μm in the model, instead of the anticipated 118 μm calculated from the tc and fed into the model. Still, the results are in good agreement as they approximate the experimental behavior.

3.2 Increase of viscosity yields smaller cavitation bubble

In the next step, the viscosity was increased, both in the experiment and in the model. The experimental results for the pressure transient, measured with the needle hydrophone with different gel concentrations in the objective-based setup, showed a decrease of the time tc, which means half of the time interval between the initial pressure wave caused by the expansion and the first collapse, decreases with increasing viscosity (cf. Figs. 3, 5d). This is related to a strong decrease in the bubble maximum radius. The simulation showed that an increasing viscosity for a constant maximum bubble radius results in an increase of tc. Hence, the decrease of the maximum bubble radius with higher viscosity has to overcome this effect (cf. Fig. 4a–c).

Fig. 5
figure 5

Simulation results for bubble near a rigid boundary (at the top of the depicted image section) for an initially spherical bubble with Rmax = 118 µm, Rn = 26 µm, pexc = 1.31 GPa; distance to the boundary from the bubble center was = 2 Rmax; a phase parameter (blue = gas inside the bubble, red = liquid outside) approx. 34 µs after the start of the simulation; b modeling results for pressure transient probed by a sensor placed at 5.6 mm from the bubble center

Full size image

The smallest tc which was possible in the simulation with a viscosity of at least 1 × 10−6 m2/s was 8 µs and fits the experimental results of a gel concentration of 7.5 g/l (cf. Fig. 3d). However, for higher viscosities, only longer tc results were possible. This does not fit the experimental results, which show a further decrease of the tc with increasing viscosity.

3.3 Bubble with nearby boundary and in a confined volume

For a later application in the inner ear, the effects of a bubble near a rigid boundary and, in a second step, inside a small, confined volume, were modeled.

The expansion of the initially spherical bubble was almost symmetric, with a slightly decelerated growth towards the boundary. During the first collapse, the complete bubble moved rapidly to the boundary, and a part of the bubble was accelerated towards its center, such that the bubble deformed to a toroidal shape due to a jet-like behavior with velocities of up to approx. 180 m/s in the center of the torus. At the end of the collapse, the jet reached the boundary (Fig. 5a).

The peak amplitudes were reduced to approx. 2/3 than in the spherically symmetric case. After the peaks, additional oscillations followed, which were not present in the spherical case (Fig. 5b). These oscillations had a different shape, amplitude and time course when the sensor position was changed. They were caused by the reflection at the boundary.

For future applications of our tone generation setup in the inner ear, a fiber delivery method was added to the setup. The laser focus was created by two ball lenses glued to the fiber end and had a distance of approx. 150 ± 10 µm to the last rigid surface of the lens, as estimated with Zemax software. In the fiber setup (Fig. 6d), the pressure amplitude was smaller and the oscillations after the expansion and collapse pressure waves had a remarkably higher amplitude than in the objective-based setup (Fig. 6a–c). The effect of adding oscillations to the original wave in the fiber setup is comparable to the result of the simulation for a wall near the cavitation bubble (Fig. 5b).

Fig. 6
figure 6

Experimental results for pressure measurement with needle hydrophone with variation of distance between the laser focus (i. e. place of bubble) to the next boundary, which is the optical window of the water container in the objective-based setup for a–c, and for d the ball lens glued to the fiber end in the fiber setup

Full size image

This deviation between the experiments in the objective-based setup and the fiber setup is explainable by the different bubble radii. The distance between the focus and the rigid ball lens boundary was approx. 150 µm for the fiber setup. In contrast to this, the smallest applied distance to the next rigid boundary was approx. 1 mm. The pressure measurements show that the influence on the bubble dynamics is negligible in the objective-based setup, but strong in the fiber setup.

To further investigate the explicit influence of the cochlear geometry on the pressure transient, a cylinder of length 22 mm and radius of 1 mm was modeled, as these values are the typical dimensions of a human cochlea, for the complete acoustic pathway over the two basal turns, measured in the central radial position [24]. The bubble was designed identical to the basic spherical bubble in water with Rmax = 118 µm, Rn = 26 µm, pexc = 1.31 GPa and the kinematic viscosity of water (1 × 10−6 m2/s) (cf. Fig. 2a). The bubble was placed at a distance of 1 mm to the rigid wall and the probe sensor locations were in a longitudinal direction at 6 mm and 20 mm from the bubble, in radial direction at 1 µm, 500 µm and 900 µm from the center.

In contrast to the basic spherical case without rigid boundaries, the bubble did not expand up to its maximum radius in the cochlea-like volume, but only up to approx. 70% of Rmax, where the collapse started. This is caused by the confined volume with rigid boundaries everywhere except in one small open end of the cylinder. Furthermore, the bubble developed a non-spherical shape and the effective radius development (radius calculated from the volume) was asymmetric during the expansion and the first collapse (Fig. 7a). Also, the pressure amplitude of the expansion and the collapse were different than in the case without a confined volume (cf. Figs. 2, 7b). Different radial sensor locations revealed that the maximum pressure was reached in the center of the cylinder. In comparison to the simulation with only one rigid boundary, the oscillations after the initial pressure peak are slower, longer lasting and their amplitude showed a weaker decrease over time.

Fig. 7
figure 7

a Simulation results of effective radius. The bubble is not spherical due to the confined volume. b, c Simulation of effective pressure development for the case of a bubble inside a cochlea-like confined volume with the same bubble parameters as in the spherical simple case. The first collapse is slowed down, such that the radius development is asymmetric. Pressure probes were taken at longitudinal distances of 6 mm (b) and 20 mm (c) from the bubble center. While the radial sensor position leads to different pressure signals near the bubble (b), this is not the case for a larger distance (c): here, the three probe locations cannot be distinguished

Full size image

4 Discussion

In our earlier study, we found that viscous media around the laser focus led to an attenuation of higher frequency components of the pressure transients generated by the laser pulses [3]. The experiments with high time resolution showed that with increasing viscosity, the time between expansion and first collapse shortens. This corresponds to a decrease in the maximum bubble radius with increasing viscosity. In the highest viscosity regime, there was no collapse measurable, likely because it is too small to be distinguished from the background noise.

In the computational model, an increase in viscosity leads to a slower expansion and thus to a longer time between expansion and first collapse. For water, the maximum bubble radius was calculated via Eq. (2). However, this was not valid for the viscous gel. Hence, three parameters had to be fit in the model: maximum and equilibrium radii of the bubble (Rmax and Rn), and excess pressure pexc that drives the initial expansion of the bubble. The maximum cavitation radius has to be sufficiently small to model the experimental result of the shorter intervals. The model could mimic the experimental pressure transients for medium viscosity but was unable to simulate the shortest measured intervals at high viscosities.

One reason is that the application of higher viscosities was only possible with assumptions within the model. Especially, the non-Newtonian viscosity of the applied gel could not be monitored within the model. Hence, the exact value of the viscosity for the relevant high-frequency regime was not indisputably extrapolatable from the viscosity measurements in low frequencies. Still, polymer gels show Newtonian plateaus for low and high frequencies and support the approximation of our study [23]. In addition, the optical investigation of bubble dynamics in polyacrylamide gels by [26] showed that for geometries without a nearby boundary, non-Newtonian effects are negligible. For future improvement of the precision, high-frequency viscosity measurements with a method shown by [27] might be promising. Additionally, the model assumes adiabatic and barotropic conditions and neglects condensation and evaporation and hence cannot model the precise bubble oscillation process.

Despite all these obstacles, the experimental results for the viscosity variation could be modeled by the simulation for medium viscosities. This was not possible for the highest viscosities. The reason is the strong decrease of the maximum bubble radius in the model that was necessary to approximate the experimentally observed decrease of tc with increasing viscosity. For viscosities corresponding to gel concentrations of 10 g/l or more, extremely small bubbles would be necessary to reach the experimentally measured tc values around 4 µs, requiring significantly higher computational power for the model calculations.

The observed decrease of the time constant of the bubble collapse with increased viscosity is congruent with modelling results via Chebyshev spectral collocation method by [28] and via Levin–Voigt-based viscoelastic model by [29]. Similar results were observed by experimental investigation of the bubble maximum radius with direct visualizations of the collapse in polyacrylamide gels by [30] and agarose gels by [31]. This study found that the maximum radius of the laser-generated bubble decreased with increasing viscosity, which was also observed by [30]. A quantitative comparison is however not possible as the PNC 400 gel of this study is by far less stiff and elastic than the gels applied by [30, 31]. For further review of bubble modelling in viscoelastic media, see [32,33,34,35,36,37,38].

The applied model is a further development of the Gilmore model. A detailed comparison of the OpenFoam model to the Gilmore model was conducted by Koch et al. who showed that both models were comparable until the first rebound and that the OpenFoam model fitted the second rebound better than the Gilmore model [15]. Furthermore, they found that the Gilmore model resulted in a slightly larger collapse time and a larger rebound radius than the full Navier Stokes equations used in OpenFoam. Another comparison was done by [15] to the Keller–Miksis model with the result that its applicability was limited to Mach numbers below 0.82 and already there the pressure is underestimated.

For future applications in the inner ear, we investigated the influence of a confined volume. The modeling of both the intermediate step of geometry with one nearby rigid boundary and a cylinder of cochlea-like dimensions was successful and revealed the influence of the boundaries on the bubble dynamics. Singular aspects of the identified phenomena, such as the jet-like behavior and the separation of the bubble, were also reported by, e. g., Lauterborn et al. from both experimental and computational results [13]. Both Koch et al. [15] and Supponen et al. [39] found that the bubble near a rigid boundary leads to a toroidal bubble shape, coherent with the results of our work. In congruence with our modeling results, Supponen et al. measured several shock waves additional to the single pressure waves by expansion and collapses. They attributed those additional waves to the jet formation. According to our results, it is more likely that the additional oscillations are due to the reflections from the rigid boundaries, as their time interval to the first pressure wave varies depending on the probe location (cf. Appendix, Fig. 9). Also, the slow-down of the collapse in the cochlea-volume in our model results, leading to an asymmetric pressure wave, was found by Koch et al. already when a single boundary is present near the bubble [15]. As a recent study by Lechner et al. on bubble dynamics directly at a solid boundary in viscous liquids found, strong bubble deformation and jetting occurs for low and medium viscosities but the speed of the jet decreases with increasing viscosity and the highest studied viscosity showed no jetting any more [40].

For quantitative investigations of the prospective design of a hearing device via optoacoustic stimulation, a more complex geometrical model of the cochlea might be applied, such as the one developed by [41].

5 Conclusion

In this work, we adapted the computation model for bubble dynamics in OpenFOAM by Koch for a viscosity study and investigation of the effect of a nearby rigid boundary and of the confined volume with cochlea-like dimensions.

The general experimental effects of the increase of viscosity, which enabled us in our earlier study to attenuate the higher harmonic frequency components, are both a decrease in pressure amplitude and in the time interval between the expansion and the first collapse. Our model results lead to the assumption that the maximum size of the bubble strongly decreases with increasing viscosity. This could be the main reason why the higher frequency components are attenuated, as reported by our earlier study [3].

By comparison of the simulation with the experimental results, the cavitation bubble dynamics in our optoacoustic tone generation setup could be understood in more detail and the effects for a future application within the cochlea were studied. At this point, no experimental data are available for the application inside the cochlea with its more complicated shape and rigid boundaries as well as compliance in different directions. Future experiments are planned to investigate whether the tone generation inside the cochlea is similar to the results of our previous study in the water container. [3] With the computational results for the geometry of similar size, the tone generation in the inner ear should be feasible.