1 Introduction

Snow is a nonlinear, time-dependent, viscous, and highly compressible material. These factors, combined with a highly variable microstructure, make the determination of snow properties ambiguous. Nevertheless, there have been tremendous amounts of experimental work to quantify the mechanical properties of snow. Some examples include studies by [7,8,9, 11, 12, 15, 19, 21, 22, 25, 26, 31, 32, 34,35,36]. A comprehensive overview of snow mechanics can be found in [20, 23, 28]. Despite all the researches conducted so far, a more comprehensive study on the mechanical properties of snow, with the aid of state-of-the-art tools like \(\mu\)CT imaging can provide more insight into the mechanical properties of snow and the deformation mechanisms. Usage of such tools with appropriate material modeling enables us to obtain more detailed description of the material parameters including both modulus and viscosity terms to account for visco-elastic/plastic behavior of snow.

Mechanical properties of dry snow are mainly related to its density [20, 27]. Dry snow is essentially a highly viscous material, and visco-elastic or visco-plastic models are common to use to model its mechanical response [20, 27]. The Young’s modulus perhaps is the most relevant parameter and the easiest to apply in engineering applications [20]. However, measuring the elastic modulus of snow can be difficult or even misleading, as pointed out by Mellor [20]. Most published results cover the quasi-static range, where the strain rate is \({\dot{\epsilon }} < 4 \times 10^{-4}\) 1/s. Increasing the strain rate to \({\dot{\epsilon }} \approx 10^{-3}\) 1/s does not make a significant difference [24]. However, for higher strain rates, i.e. \({\dot{\epsilon }} > \times 10^{-2}\) 1/s, the Young’s modulus increases, which is typical for a visco-elastic material [30]. In essence, when obtaining the modulus directly from the stress–strain curve, it is important to consider it as an “effective” modulus because the time dependency of the strains is included in the measurements [15].

\(\mu\)CT-based methods have recently been used in snow mechanics to obtain a better understanding of the micromechanics of snow. One challenge during the \(\mu\)CT investigation is to obtain a representative sample size, as many machines have limitations on the maximum object size allowed. Coleou et al. demonstrated that for a typical snow grain size of roughly 150 \(\upmu\)m a cylindrical Representative Elementary Volume (RVE) of 9 mm in both diameter and height provides a statistically adequate representation of the macroscopic structure of snow [9]. In practice, this means that the sample volume needs to be at least 50 times larger than the typical grain size in order to provide reliable results on the macro-response. \(\mu\)CT offers many inherent advantages for testing granular materials. For example, the images can serve as structural input for a FEM analysis [26]. Further, \(\mu\)CT images can be combined with time-dependent models to study microstructural changes and mass transfer of dry snow [21] as well as to investigate the structural evolution under loading [34]. One interesting application of \(\mu\)CT-based FEM is to estimate the elastic modulus of snow. For example, Chandel et al. [8], found that snow hardens at loading rates smaller than \(4.8 \times 10^{-5}\) 1/s but softens for higher rates, at least up to 4.8 \(\times 10^{-4}\) 1/s. Similarly, the microstructure of snow was related to its macroscopic elastic stiffness tensor through a series of micro-tomography based FEM calculations [31, 35]. As another example, Reuter et al. have shown that micro-penetrometry of snow and \(\mu\)CT-derived moduli can be related by considering the anisotropy of snow [22]. In addition, \(\mu\)CT-assisted discrete element calculations have successfully been used to study and analyze the mechanics of snow. For instance, the mixed-mode failure of snow was studied using this method [19]. As a complement, advanced image analysis techniques such as Digital Volume Correlation (DVC) have successfully been used on 3D structures of snow obtained from \(\mu\)CT to calculate 3D displacement fields inside snow samples [12].

The combination of \(\mu\)CT and mechanical loading can be used to identify material properties of interest [6, 37]. When studying snow, it is important to consider the material properties beyond conventional Young’s modulus. This is because both ice and snow display significant visco-elastic properties, and the effects of viscosity should be taken into account [17, 20, 27, 29, 32]. One underlying mechanism of the viscous behavior of snow is sintering, which leads to binding forces between ice particles and is known to increase over time [1, 33]. The visco-elastic properties of single and polycrystalline ice were represented by a model consisting of Voigt units in series with Maxwell units using experimental methods, but the properties of snow were not investigated [16]. The Burgers model, a fusion of the Maxwell and Voigt models, is widely referred to in the analysis and design of visco-elastic materials [3, 10, 20].

In this study, we aim to map the density-dependent visco-elastic material properties of dry manufactured snow using step-wise, quasi-static, uni-axial loading imaged under \(\mu\)CT. We correlate the estimated properties with the density of snow using \(\mu\)CT imaging. In addition, DVC calculations are performed to explore the deformation regime within the snow sample to identify potential deformation localization regions. A brief literature review and motivation are provided in the current section, Sect. 1. The materials and methods, including sample preparation, \(\mu\)CT imaging, DVC, density estimation, and the visco-elastic model used in this study, are described in Sect. 2. The results are provided in Sect. 3, and a discussion about the results and limitations is presented in Sect. 4, followed by a conclusion about the key findings in Sect. 5.

2 Materials and methods

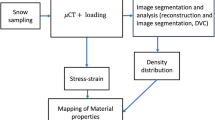
The experimental procedure is outlined in Fig. 1. The left part of the image represents the process of snow manufacturing and how it is prepared for measurement. This process is further detailed in Sect. 2.1. The central column represents the measurement, which is performed in a micro-tomography X-ray machine (\(\mu\)CT). During measurements, the snow sample is kept at a constant temperature and compressed uniaxially in small steps while monitoring the force response. Similar to [12], at each compression level, the sample is positioned in the CT machine and is kept there to stabilize until the force-displacement variations are small enough (so the movements in the sample cannot create imaging artifacts), the structure is recorded by the CT machine. With this approach, we have access to both the time-resolved force response and the density distribution at each compression level, which serve as inputs for further analysis. The entire procedure is detailed in Sect. 2.2. The right part of Fig. 1 represents the analyses that are performed on the data provided by the experiments and are detailed in Sect. 2.3. The force response acquired is fitted to a visco-elastic model known as Burger’s model, which includes two stiffness terms and two viscosity terms, respectively. After reconstruction, the \(\mu\)CT data are segmented, providing the volume fraction of snow at each load step.

Fig. 1
figure 1

Schematic of the steps conducted to obtain density resolved material properties of dry snow

Full size image

2.1 Snow preparation

Freshly manufactured snow was collected from Arctic Falls Indoor Flex facilities in Piteå, Sweden. The temperature during the production was − 7 \(^\textrm{o}\)C and the production process involved spraying water vapor into the air. Water is pressed through the fine nozzles of snow machines at high pressure and is sent out as tiny droplets which freeze quickly in the cold air when they come out of the nozzles. These frozen droplets fall to the ground as grains of ice and their aggregate forms a bulk of manufactured snow. The entire production process took approximately 45 minutes. Snow was collected by shoveling it into glass containers with dimensions of approximately 20 \(\times\) 10 \(\times\) 5 cm\(^3\) right after production. The containers were then placed in a freezer with a temperature of approximately − 21 \(^\textrm{o}\)C and transported to Luleå University of Technology (LTU). The temperature of the freezer was kept at − 21 21 \(^\textrm{o}\)C to minimize the sintering and metamorphism effects, which can otherwise alter the properties of the snow by promoting bonding between the grains. The snow samples were then transferred to a larger freezer with dimensions of 2 \(\times\) 1 \(\times\) 1 m\(^3\) and were kept at a constant temperature of − 21 \(^\textrm{o}\)C. This temperature was the minimum reachable temperature of the available freezer. The maximum storage time was 5 days.

Snow was sampled from the containers and placed into Polymethyl methacrylate (PMMA) tubes having an internal diameter of 9 mm, wall thickness of 1 mm, and a height of 11 mm. An aluminum plate was chosen as the base plate of the snow sample, as observed in Fig. 2, to ensure a good heat transfer to the cold metallic plate of the actuator in the \(\mu\)CT machine to minimize any possibility of local melting due to the CT radiations in the snow sample during the imaging process. The sampling process involved inserting the PMMA tubes into the snow inside the containers. The excess snow on top of the PMMA tube was carefully removed by gently shearing it away with a cold glass plate, without applying pressure. Finally, an aluminum punch with a diameter of 9 mm and a height of 5 mm was carefully placed on top of the snow sample before mounting it on the movable punch. During the entire handling and sampling process, extra caution was taken to prevent any contact with warm surfaces in order to avoid rapid crystallization that could initiate from the container walls.

Fig. 2
figure 2

Experimental setup: (Left) the experimental environment; (Right) the snow sample mounted on the punch. Numerated items, 1: \(\mu\)CT source, 2: temperature controlled in-situ load stage, 3: Granite base, 4: Magnification tunable detector with 2k \(\times\) 2k 16 bit CCD camera, 5: 4-axis, motorized precision sample stage, 6: Fixed punch, 7: PMMA tube containing snow, and 8: Movable punch

Full size image

2.2 Micro-CT imaging and testing

The snow sample and its placement in the \(\mu\)CT machine are shown in Fig. 2. Numbers 1–5 refer to details in the machine, while numbers 6–8 indicate details of the snow sample mounted on the punch. The \(\mu\)CT system used was a ZEISS Xradia 620 Versa (Carl Zeiss X-ray Microscopy, Pleasanton, CA, USA). As indicated in Fig. 2, it consists of a sealed microfocus X-ray tube, a 4-axis sample stage, and a high-resolution detector, all mounted on a stable granite block. An in-situ load stage (CT5000TEC, Deben UK Limited, Bury Saint Edmunds, UK) with a 500 N load cell was added to the system. This load stage allowed for the application of controlled loading and the measurement of displacement and force in a temperature-controlled environment.

All experiments were performed at − 18 \(^\textrm{o}\)C. The temperature was kept constant with variations of 0.01 \(^\textrm{o}\)C. The sample was loaded in displacement-controlled mode, with a total compression of 4 mm divided into 7 steps, see Fig. 10b. The loading speed was 0.2 mm/min. Similar to [12], at each plateau, the sample was allowed to relax by visually checking the stress variations during the relaxation before and then the tomographic image acquisition was started. In other words, when the load cell showed minimal fluctuations in force over time, or when the slope of the force-displacement curve was low, the skilled CT operator could anticipate that the upcoming imaging would likely not yield significant changes in the snow structure that could generate artifacts. The force data was consistently recorded and subsequently normalized by the inner cross-sectional area of the tube to determine the average stress applied to the sample.

The X-ray source voltage and power were set to 80 kV and 10 W, respectively. A total of 801 projections were recorded, resulting in a resolution of 25 \(\upmu\)m inside the sample. The total scan time for each load step was approximately 30 minutes, and the overall duration of the test, including relaxation time, was approximately 5.5 h. Typical examples of snow structure and stress responses are shown in Figs. 4 and 10 , respectively.

2.3 Analysis

Even though snow undergoes volume changes under loading and its material properties are truly visco-plastic [20], we can still treat snow as an “incrementally linear” material at each load step and estimate its visco-elastic properties at that particular step. In this way, density-dependent properties of snow can be extracted using a visco-elastic approximation. The model we adopt is known as Burger’s model (see, for instance [13]), which is a visco-elastic model comprised of a Maxwell and Kelvin–Voigt model in series, as depicted in Fig. 3. The differential equation describing the stress–strain relation is as follows:

$$\begin{aligned} \ddot{\sigma } + A_1 {\dot{\sigma }}+A_2\sigma = E_M \ddot{\epsilon } + A_3 {\dot{\epsilon }} \end{aligned}$$
(1)

where

$$\begin{aligned} A_1= & {} \frac{E_M}{\eta _M} + \frac{E_M}{\eta _K} + \frac{E_K}{\eta _K}, \end{aligned}$$
(2)
$$\begin{aligned} A_2= & {} \frac{E_M E_K}{\eta _M \eta _K}, \end{aligned}$$
(3)

and

$$\begin{aligned} A_3 = \frac{E_M E_K}{\eta _K}. \end{aligned}$$
(4)

The parameters \(E_M\) and \(\eta _M\) represent the stiffness and viscosity for the Maxwell part of the Burger’s model, and \(E_K\) and \(\eta _K\) represent the stiffness and viscosity for the Kelvin–Voigt part, respectively (see Fig. 3). With the application of a pulse of strain rate, \({\dot{\epsilon }} = k_1\left[ {\hat{H}}(t) - {\hat{H}}(t-t_l)\right]\) , where \(k_1 = 2\) mstrain/min is the strain rate during loading and \({\hat{H}}(t)\) is the Heaviside step function, the stress response becomes

$$\begin{aligned} \sigma (t)=\; & {} k_1 \Bigl \{\frac{E_M}{m_1 - m2} (e^{m_1 t}-e^{m_2 t}) \nonumber \\{} & {} + \frac{\eta _M}{m_1 - m2} (m_2 e^{m_1 t}- m_1 e^{m_2 t}) + \eta _M \Bigl \}\nonumber \\{} & {} -k_1 {\hat{H}}(t-t_l)\Bigl \{ \frac{E_M }{m_1 - m2} (e^{m_1 (t-t_l)}-e^{m_2 (t-t_l)}) \nonumber \\{} & {} + \frac{\eta _M }{m_1 - m2} (m_2 e^{m_1 (t-t_l)}- m_1 e^{m_2 (t-t_l)}) + \eta _M \Bigl \} \end{aligned}$$
(5)

where, \(t_l\) is the duration of loading for each loading step, which is the time from the start of the deformation-controlled loading to the start of the relaxation at each loading step:

$$\begin{aligned} m_{1,2} = \frac{-A_1\pm \sqrt{{A_1}^2 -4 A_2}}{2}. \end{aligned}$$
(6)

To reach at Eq. (5) we used the initial conditions \(\sigma (0) = 0\) and \({\dot{\sigma }}(0) = k_1 E_M\). A similar solution exists in [20]). Equation (5) is the main relation from this section and is used to estimate the visco-elastic material properties from the stress–time response at each load step by performing discrete minimization of the cost function, J in the following equation:

$$\begin{aligned} J = \sum _{i=1}^{N_p} \frac{\sigma (t_i)^2-{\hat{\sigma }}(t_i)^2}{\sigma (t_i)^2} \end{aligned}$$
(7)

where \(N_p = 8\) is chosen as the number of collocation points. The points are selected in the span of start of loading to 1.2 time from the start of relaxation for each loading step. The points are selected in such a way that the maximum stress always matches one collocation point.

Fig. 3
figure 3

Burger’s model for a visco-elastic material. It is a combination of Maxwell and Kelvin–Voigt models in series. \(E_M\) and \(\eta _M\) are the stiffness and viscosity of the Maxwell model, respectively and \(E_K\) and \(\eta _K\) are the stiffness and viscosity of the Kelvin–Voigt model, respectively

Full size image

The primary software used to manage and segment the tomographic images provided by the system is Dragonfly (ORS, Montréal, Canada). One such segmentation is binary segmentation, which divides the image into “white” (representing snow) and “black” (representing air). From this information, it is possible to obtain the particle size distribution by fitting spheres to the distribution. Furthermore, the relative density can be calculated by dividing the number of black pixels by the total number of pixels in the image. This calculation was performed using Matlab (v 2022a, Mathworks, MA). In this way, for example, the relative density of a desired axial segment can be obtained by simply counting the number of white pixels (representing snow, as described above) in the slice and comparing it to the total number of pixels. The true density may then be obtained by multiplying this number by \(\rho =0.917\) g/cm\(^3\), the density of ice.

Using the Digital Volume Correlation technique (DVC), the full-field displacements of snow are obtained, and then the desired components of the strain fields are calculated through differentiation. The DVC tracks the movements of small volumes in the system during loading and estimates the displacement fields at each time step using correlation methods. A comprehensive description of the DVC technique is presented in [2, 5, 14]. The DVC analysis was carried out using LaVision Davis (LaVision Inc., Ypsilanti, MI, USA) 8.4. A multi-grid differential correlation approach was used, with a final sub-volume size of 32 \(\times\) 32 \(\times\) 32 voxels and 75% overlap.

3 Results

Sample \(\mu\)CT images and the corresponding segmented images for test 1 during the loading of the specimen are shown in Fig. 4. From this figure, the majority of the particles on the surface are in the range of the diameter of 0–200 \(\upmu\)m, as shown by blue, but from Fig. 5, we can see that there is a significant number of particles that are in the range of 200–400 \(\upmu\)m indicating internal particles. It is visually evident from Fig. 4 that the larger particles colored as red, increase toward the last loading step which indicates particles connections and sintering under the loading. The particle size distribution is presented in Fig. 5. Since the size distribution does not change significantly with the loading, it can be an indicative that the sintering and crushing effects are competing and are in a relative equilibrium.

Fig. 4
figure 4

Sample CT images for test 1 during the loading of the specimen from left to right. The first row indicates the raw images and the second raw indicates the segmented images. The color bar at the bottom of the figure shows the corresponding diameter range for the segmented images in the second row of the figure

Full size image

The data for SSA is presented in Fig. 6 and is approximately constant for all load steps. Its mean value is around 35 (1/mm) which is lower than the value of around 66 (1/mm) observed for natural snow [25].

The changes in SSA distribution during loading are presented in Fig. 6. The isothermal densification of snow under a constant external stress and imaged under \(\mu\)CT was studied in [25] and a significant increase in the density of snow was observed. The Specific Surface Area (SSA) did not show significant change under the loading.

The sphericity of the particles is presented in Fig. 7. The sphericity can be defined as the ratio of the surface area of a particle of a given volume and the surface area of an equivalent sphere with the same volume[4]. The mean sphericity clearly increases from approximately 0.5 in the first step to 0.7 in the last step.

Fig. 5
figure 5

Particle size (diameter) distribution for test 1 at different load steps: The particle mean radius is around 110 \(\upmu\)m, and does not change significantly with the loading. The total number of particles is 18341

Full size image
Fig. 6
figure 6

The distribution of the SSA for test 1 at different loading steps. The SSA is not changed significantly with the loading and the mean SSA remains around 35 mm\(^{-1}\)

Full size image
Fig. 7
figure 7

The distribution of the sphericity for test 1 at different loading steps. The sphericity of the particles increases significantly from a mean of nearly 0.5–0.7 which can be the effect of some sintering between the ice particles at higher densities

Full size image

From Fig. 8a it is clearly seen that the density increases as the punch pushes deeper into the sample. Visually, the density appears homogeneous throughout the entire loading cycle. In fact, the calculated distributions of the density at different load steps presented in Fig. 8 verify this behavior. It is evident from Fig. 8a that the density along the axial direction of the specimen remains relatively constant at a specific compression value. The corresponding density distribution in the radial direction, as presented in Fig. 8b, is seen to be nearly constant in each quarter of the specimen. As the compression progresses, the radial distribution of the density becomes more uniform, which is a clear indication of compaction.

Fig. 8
figure 8

Density variation in axial and in radial segments, respectively: a density variation in axial direction. Each of the shown curve represent the density value at the specific layer of image pixels which represent the relative axial position, b density variation in radial direction. x axis is the normalized axial position. For a specific load step, at each axial position, there are values of density indicating the averaged valued in one quarter of the cross section at that axial position. Only the steps 1, 4, and 7 are shown

Full size image

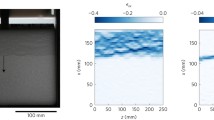
As part of a further investigation into the uniformity of compaction, a cross section of the axial strain obtained from the DVC is presented in Fig. 9. The DVC results for the deformation of natural snow exhibited severe localization [12]. The sample size used in their work was 6 mm which is smaller than the 9 mm size suggested by [9], and this can be a source of localization observed in the deformations. Another factor could be the irregular form of the natural snow particles. A possible shear band of the material is also depicted as the red dashed line. The line has an inclination of around 60 \(\mathrm {^o}\). Further analysis or discussion of the shear band is out of scope of the current work.

The nominal strain values corresponding to each DVC image in Fig. 9 are provided below, extending up to 0.42 in the final step. The axial strains exhibit relatively homogeneous behavior with some degree of localization. The nominal compressive stress, \(\sigma = F/A\), (where F is the applied force and A is the cross section of the PMMA tube), is plotted as a function of nominal strain \(\epsilon = \delta / L\) (where \(\delta\) is the imposed displacement and L is the height of the PMMA tube) in Fig. 10a. As expected, the stress increases non-linearly with increased strain. In fact, when looking in detail, the apparent Young’s modulus, defined as the slope of the stress–strain curve first decreases with strain and then increases. When the loading is stopped, the stress quickly decreases due to relaxation. It should be noted that the three different samples have been tested, and the results were similar. This indicates that the snow preparation procedure was consistent and repetitive. However, only the first test followed the complete test procedure as described in Sect. 2.2. The stress–time plot is presented in Fig. 10b. The peak that appears at each relaxation level defines the visco-elastic behavior at the corresponding level of compaction, a behavior that should also be described by Eq. (5). As an example, Fig. 11 shows three of the peaks along with their fitted results. Then, for each level of compaction, the four material parameters of interest are retrieved as depicted in Fig. 12.

Fig. 9
figure 9

Axial strain distribution obtained from the DVC for loading steps of test 1. The initial length of the specimen before beginning compression was 8.1 mm. \(\varepsilon _{\text {nom}}\) shows the nominal axial strain of the sample. The red dashed line, with inclination angle \(\approx\) 60\(^ {\textrm{o}}\), indicates a possible shear band in the material

Full size image
Fig. 10
figure 10

Stress versus strain and time for the manufactured snow: a stress–strain response shows a hyper-elastic-like behavior with no significant yielding. This figure shows three experiments as designated by tests 1–3. The drops in the curve for test 1 correspond to the relaxations in the sample during the constant displacement presented in section (b). The three test exhibit similar stress–strain behavior. b Stress–time and imposed displacement: the stress increases during the constant speed loading at each step and then decreases after the load is kept still. This figure shows the stress–time plot for test 1 in the part a of this figure. The black spheres show the approximate time of the start of \(\mu\)CT imaging

Full size image
Fig. 11
figure 11

Sample curves fitted on the stress–time response using Burger’s model (- - - represents the fitted curves using Eq. 5), — represents the measured stress–time response. The times axis shows the time from start to the end for each loading step, thus 0 shows the start time for each loading step. All the peaks correspond to the test 1 in Fig. 10a

Full size image

The four parameters corresponding to the stiffness and damping (modulus and viscosity interchangeably) of the snow are plotted against relative average density in Fig. 12. All the damping and the modulus parameters indicate an increasing behavior with the density as expected. The values corresponding to the Maxwell modulus component are an order of magnitude larger compared to those corresponding to Kelvin component. As an approximation, the power law function is used to fit mathematical relations between the modulus and damping parameters in Fig. 12. Apparently all the parameters increase with a power of nearly 4 to 5.3 in the considered range of the relative density. It is notable that the average particle size did not change significantly during the loading, as shown in Fig.  5. Therefore, the increasing properties with the loading which is translated into density in Fig.  12 might imply independence of the material properties from the particle size.

Fig. 12
figure 12

Estimated material constants using Burgers model as a function of snow density a Kelvin–Voigt modulus, b Maxwell modulus, c Kelvin–Voigt viscosity, d Maxwell viscosity

Full size image

4 Discussion

One of the challenges in snow testing is sample preparation. During the process of snow sampling, it is crucial to obtain a homogeneous snow sample. For snow residing at temperatures around − 20 \(\mathrm {^o}\)C, the punching method is effective in transferring the snow from the container into the small tubes. This method appears to ensure consistent and repeatable sample collection. The three different uniaxial compaction tests presented in Fig.  10a resulted in relatively repeatable stress–strain responses. Snow is after all a variable material and it is not possible to obtain exactly the same behavior under different experiments. The differences in the observed stress values are quite pronounced for lower strain values (less than 5 percent strain) and the percentage of variations can be as high as 50%, but at higher strains toward the end of the compaction, the variations are around 10% for strains not too close to zero. The conclusion is thus that the sampling method used in this investigation results in sufficient homogeneity and repeatability. That said, a higher variation exists between the stress values between three different tests in low strains which is in the beginning of the compaction. It is therefore important to have a sample size that can properly represent the statistical distribution of the snow. In this investigation, we used a cylindrical sampling volume of 9 mm in both radial and axial direction as previously suggested to ensure grain independence [9]. The results from this investigation appears to verify their conclusion. In fact, the distribution of particles as presented in Fig. 5 shows that the particles are roughly spherical and that the most common particle radius is around 100 \(\upmu\)m. Almost no particles are larger than 180 \(\upmu\)m, which means that more than enough particles fill up the measurement volume. The fact that the distribution resembles a log-normal distribution is a further indication that the sample volume is representative for the snow investigated.

The stress–strain curve shown in Fig.  10a is very similar to the stress–strain curve of foam materials [18]. Typically it shows an initial linear stress–strain regime until it reaches a very small initial yield strength, followed by a highly nonlinear stress–strain curve that resembles a hyperelastic material behavior. From the shape of the curve these values are expected to increase rapidly with increased compaction. It should be noted that these values relates to snow that is predominantly spherical and largely non-bonded, making it difficult to compare with results from other type of snow found in literature [27]. More importantly, one should note that this is only the apparent modulus, as highlighted in [20]. Focusing instead on the stress–time response shown in Fig. 10b it is possible to estimate the viscoelastic material properties of the manufactured snow, through the use of Eq. (5). A fit is shown in Fig. 11 and the parameter estimation is shown in Fig. 12. The results for the Maxwell and Kelvin–Voigt moduli were found to range from 60 to 320 MPa and from 6 to 40 MPa, respectively. The viscosity values for the Maxwell and Kelvin–Voigt models varied from 0.4 to 3.5 GPa-s, and 0.3–3.2 GPa-s, respectively. As expected the result for the Maxwell stiffness agrees well with the estimation of the Young’s modulus from the stress–strain curve. One should note that these values increase drastically with compaction and that within the range considered the increase is in proportion to the power of 4–5.3 of the relative density. However, the increase is likely to be even higher for higher densities. As mentioned in [27], Mellor [20] decomposed the viscosity into “axial” and compactive terms, with the former being equivalent to the Maxwell viscosity in the four-parameter (Burgers) viscoelastic model. The lower bound of the reported data varies between 50 and 1000 GPa-s for a density range of 450–600 kg/m\(^3\). In our experiments with non-sintered, manufactured snow, the viscosity values are much lower, ranging from 0.3 to 5.3 GPa-s, for a density range of 400–690 kg/m\(^3\). The results obtained from our experiments show that both the modulus and viscosity values for the non-sintered snow are much lower than for the sintered one. The handling of snow is therefore of paramount importance when determining its mechanical properties.

The average particle size remained relatively unchanged throughout the loading process. However, a meticulous analysis of the particle size distribution, particularly when plotted on a logarithmic scale, reveals an increase in number for both larger and smaller particles under loading conditions. This observation suggests an ongoing interplay between sintering and crushing effects within the snow during loading, resulting in a nearly consistent mean particle size. The particle sphericity shifted from approximately 0.5 to 0.7, indicating potential sintering effects caused by the melting and freezing under pressure, leading to a more rounded particle shape. Conversely, the specific surface area (SSA) exhibited minimal change during loading, remaining nearly constant, which aligns with the overall observations [25]. Finally, we may note a small deviation from a pure axial compression test appearing in our results. First, considering the evolution of the relative density presented in Fig. 8 it is obvious that the density planes representing the relative density in the radial direction are tilted slightly.

In the beginning they are tilted towards the right and change into a small leftward tilt for the later load steps. Looking instead at the measured strain distributions presented in Fig. 9, we first see a distinct strain localization in the upper right corner before a slightly tilted structure appear. This suggests that the upper snow surface might not have been precisely horizontal, or the force direction may not have perfectly aligned with the cylinder’s axis, or both. In essence, a small redistribution of snow grains have appeared in radial direction. However, the axial strain fields are to a large extent homogeneous with an average value close to the nominal strain. This study can open up a methodology for a thorough investigation of density-dependency of the snow material properties by using the proposed mechanical model and step-wise loading. The visco-elastic properties of snow are also dependent on frequency. The dynamic modulus increases with frequency, while viscosity decreases. However,this research focuses on quasi-static density dependency of the material properties and ignores the frequency dependency.

5 Conclusions

Comprehending the mechanical attributes of snow holds significant importance across diverse domains, including cryospheric studies, polar exploration, and construction applications. The method estimates mechanical properties of snow successfully. The methodology presented here may be transferred to a great variety of different types of snow in future. We have plans to present similar results for natural snow. The procedure has great flexibility and allow full control of both grain size and distribution as well as a possibility to study effects of strain localization and other geometrical effects. By mapping the properties of snow with densities ranging from 400 to 600 kg/m\(^3\), we reported the found the four material parameters using Burger’s model to be Maxwell and Kelvin–Voigt moduli were found to range from 60 to 320 MPa and from 6 to 40 MPa,respectively. Meanwhile, the viscosity values for the Maxwell and Kelvin–Voigt models varied from 0.4 to 3.5 GPa-s, and 0.3–3.2 GPa-s, respectively. Moreover, via DVC analysis, we could observe more uniform displacement distribution compared to the previous works. We also found the change in the distribution of the particle size, SSA, and particles’ sphericity and observed that while the latter increases with the loading, the two former remain nearly constant. The methodology presented here adequately captures the density-dependent material properties of snow. Nevertheless, there exists potential for several extensions to enhance its scope. For example, considering the impacts of temperature variations and the degree of sintering in snow would be advantageous. By altering temperature and sintering levels, it’s possible to derive a comprehensive map of material properties. Notably, the snow in this study was primarily non-sintered. Another avenue for refinement involves expanding this methodology to encompass a more extensive array of samples. This would enable the capture of the statistical characteristics of material properties, such as mean values and standard deviations.