1 Introduction

Fogging of glasses is a widespread and well-known problem still searching for solutions. It occurs on the surfaces of objects that are colder than their humid environment. This is, e.g., the case for eyeglasses, if the wearer walks from the cold outside into a warm room, or for bathroom mirrors, if someone is taking a hot shower. Further examples for glasses that are frequently affected by fogging are helmet visors, diving goggles, car mirrors, or windows in general. The problem of fogging is that water condenses in form of small droplets on the surface. These droplets scatter the transmitted light, and thus cause blurred vision through the glass. See Fig. 1a, b. Anti-fogging surfaces avoid the formation of scattering droplets on a surface. This can be achieved by improving the wettability of the surface such that the droplets are spread completely across the surface [1]. This wetting state is called superhydrophilic; the required water contact angle is θ < 5. The Wenzel model implicates that the contact angle depends on the roughness ratio r, which is defined as the ratio of the true area to the apparent area, and the contact angle of the plain surface θ0 [2],

$$\cos \theta = r\cos \theta_{0} .$$
(1)
Fig. 1
figure 1

Light scattering on dry (a) and fogged (b) glass surfaces. Anti-fogging surfaces have rough surfaces (c, d) to provoke spreading of the fog droplets on the surface (d). As a consequence, light scattering increases in the dry state (c) but reduces in the wetted state (d). The challenge is to find the optimal structure to achieve perfect wetting and minimal scattering (indicated by the red arrows) at the same time. For this purpose, single (e) and/or double-hierarchical structures (f) were generated on the glass surface using ultra-short-pulsed laser processing

Full size image

Glass is already intrinsically superhydrophilic. However, contaminations by airborne hydrophobic organs raise its contact angle typically to about 20°–30° [3]. To compensate this natural effect, the roughness ratio of glass should be 1.05 < r < 1.15, or in simple terms the surface should be increased by 5–15%. However, rough surfaces scatter light in the dry state. Thus, the key to a perfect anti-fogging surface is to roughen a surface such that light scattering is minimal in both the unwetted (Fig. 1c) and the wetted (Fig. 1d) state.

Examples of superhydrophilic surfaces can be found in nature, e.g., on various plant surfaces [4], lizards [5], or tropical flat bugs [6]. These kind of structures were mimicked on glasses by deposition of nanoparticles [7, 8] or nanofibers [9], applying porous or rough coatings [10,11,12,13,14,15,16,17], or by direct roughening of the glass surface by chemical etching [18] or laser structuring [19,20,21]. Among all those methods, laser processing has several advantages. Because it is a maskless technique enabling direct writing of arbitrary geometries on the glass, coatings are unnecessary and the generated surfaces are thermally, mechanically, and chemically resistant. In particular, ultrashort-pulsed lasers are of special interest for glass processing. The ultrashort pulse durations and extreme intensities reduce thermal side effects to a minimum and enable non-linear absorption in nearly any material, respectively. Consequently, transparent and brittle materials, such as glasses, can be processed crack and melt-burr free. A further advantage, which attracts many researches to use ultrashort-pulsed lasers for surface processing is the arise of laser-induced periodic surface structures (LIPSS) in form of ripples during processing [22]. The ripple period, which is typically in the order of a few 100 nm [23, 24], is slightly smaller than the wavelength of the laser used [24, 25]. The ripples tend to melt together to larger structures when using longer pulse durations [26]. Ultrafast lasers have been used frequently to generate LIPSS to fabricate superhydrophobic or superhydrophilic surfaces [27,28,29,30]. To estimate the influence of LIPSS on wettability, we approximate a sawtooth-like shape for the ripple profile (see Fig. 1e). Because ripples have about the same depth and period [23], ar = pr, their roughness ratio can be simply estimated to be \(r_{{\text{r}}} = \sqrt {1 + {{4a_{{\text{r}}}^{2} } \mathord{\left/ {\vphantom {{4a_{{\text{r}}}^{2} } {p_{{\text{r}}}^{2} }}} \right. \kern-\nulldelimiterspace} {p_{{\text{r}}}^{2} }}} = \sqrt 5 \approx 2.24\). LIPSS appear automatically also on the surface of laser-ablated holes, scribes, and cavities. The period of laser-fabricated holes, trenches or crosshatch patterns depends on the diameter of the laser beam in the focal plane and ranges typically from a few µm to several 100 µm. In this way, double-hierarchical structures can be fabricated in a very convenient way as demonstrated, e.g., on metals [28, 31], semiconductors [32] or dielectrics [19]. Due to the superposition of LIPSS with the ablated geometry (See Fig. 1f), their roughness ratios multiply, and the total roughness ratio of the generated double-hierarchical structure can be estimated to be \(r_{{\text{h}}} = \sqrt {1 + {{4a_{{\text{h}}}^{2} } \mathord{\left/ {\vphantom {{4a_{{\text{h}}}^{2} } {p_{{\text{h}}}^{2} }}} \right. \kern-\nulldelimiterspace} {p_{{\text{h}}}^{2} }}} \cdot r_{{\text{r}}} = 5\). On the one hand, this simple calculation indicates that LIPSS and ablated geometries cause different roughness ratios. On the other hand, the estimated roughness ratios of both structures are more than sufficient to make glass surfaces superhydrophilic. This means that the glass surface could be processed only partially to achieve anti-fogging properties, e.g., by ablating rippled spots, holes, or scribes with a certain pitch, while transmission should increase with the area of the unprocessed surface.

The aim of this study was to evaluate the transmission of a glass surface structured with a pattern just small enough to generate a superhydrophilic glass surface. Because circles are the easiest and smallest elements to achieve with laser structuring, circular spots with LIPSS (Fig. 1e) and holes (Fig. 1f) were selected as base periodic elements. Patterns of these two elements were fabricated with varying pitch x and their influence on wettability and transparency was investigated. Then, a processing strategy to obtain contact angles of θ < 5° with highest transmission was selected, and the influence of the generated structures on the visual perception of objects imaged through glasses placed close to the image and lens plane in the dry and wetted state was investigated.

2 Materials and methods

The substrates used were 4″ borosilicate glass wafers with a thickness of 500 μm (BOROFLOAT 33, Schott, Mainz, Germany). The samples were stored in a clean-room environment (ISO class 5, T = 21 °C). The wafers did not undergo any cleaning before the structuring process.

The laser structuring experiments were carried out using an ultrashort-pulsed laser (Spirit, Spectra-Physics, Rankweil, Austria) with the following specifications. The pulse duration was about 380 fs (FWHM). The laser could be operated at a wavelength of λ = 1040 nm or λ = 520 nm. Because of the higher absorption of glass at the latter wavelength, all experiments in this study were carried out at λ = 520 nm. The laser source could be operated at a pulse frequency between 100 kHz and 1 MHz. All experiments were carried out using a pulse repetition rate of frep = 100 kHz, because the laser system provided maximum pulse energy and power at this pulse frequency. The maximum power and pulse energy available behind the focusing optics were measured to be P = 1.1 W and E = 11 µJ, respectively. The pulse energy was controlled using an integrated attenuator. The laser source was integrated in a laser-processing machine (microSTRUCT vario, 3D-Micromac, Chemnitz, Germany). A galvanometer scanner was used to translate the laser beam across the sample. The focusing optic was a telecentric f-theta lens with a focal length of 100 mm. The available scan field had a size of 60 × 60 mm2. The focus radius was determined to be w0 ≈ 6 µm using the method suggested by Liu [33]; the Rayleigh length resulted to be about 200 µm. The laser beam was linear polarized.

The laser-structured patterns were dot matrixes of rippled dots and holes, which were fabricated as follows. First, the beam was translated to the desired position. Then, the pulse picker of the laser source, which is an acousto-optical modulator (AOM), was opened for the time t = N/frep to apply N pulses to this position. Finally, the beam was translated to the next position. It should be noted that laser and scanner were not synchronized and the gate for the AOM was slightly shorter than the pulse period. Thus, about every 1000th dot was irradiated with N-1 pulses. The morphology of the irradiated positions could be controlled by means of the applied fluence F and number of pulses N. Preliminary experiments were performed to determine parameter sets to generate rippled dots and holes. These results showed that smooth crater forms after N < 5 pulses, ripples occur after N = 5–10 pulses, and holes form after N > 10 pulses, which was also observed in several other studies [26, 34, 35]. Chippings were observed at F ≥ 3.4 J/cm2, thus, the fluence was set just below this value to F = 2.6 J/cm2 to maximize the modified area. This fluence was used to generate both ripples and holes. The ripples were generated with N = 5 pulses (see Fig. 2a) and the holes with N = 50 pulses (see Fig. 2b).

Fig. 2
figure 2

Single spots with rippled circles (a) and holes (b), and patterns of rippled circles (c) and holes (d) fabricated on a glass wafer after irradiation with N = 5 (a, c) and N = 50 pulses (b, d) at a fluence of F = 2.6 J/cm2. The diameters of the rippled circle (a) and hole (b) are dr = 5 µm and dh = 10 µm, respectively. The pitch between both rippled spots (c) and holes (d) is x = y = 20 µm

Full size image

To investigate the influence of the processed area on surface wettability and transmission, 7 × 7 mm2 squares filled with ripples and holes of varying pitch x were fabricated on a glass wafer. The ripples and holes were arranged in an orthogonal symmetry (see Fig. 2c, d) due to the simple programming and calculation of the processed area. The pitch x was varied between 10 µm and 1 mm while the step size was increased from 5 to 100 µm.

As Fig. 2a, b reveals, the diameters of the rippled spots and holes, dr and dh, are different. To perform a reasonable comparison between both structure types, the ratio of the processed area was calculated as:

$$f_{{\text{r,h}}} = \frac{{A_{{\text{r,h}}} }}{{A_{0} }} = \frac{{d_{{\text{r,h}}}^{2} \pi }}{{4x^{2} }},$$
(2)

where Ar or Ah are the areas of the rippled spots and holes, and A0 is the square of the pitch x. At N = 50, chippings occurred when the pulses were set closer than about x = 30 µm, as can be seen, e.g., for x = 20 in Fig. 2d. At N = 5 pulses, chippings were not observed for any pitch x, as, e.g., shown for x = 20 in Fig. 2c. It should be noted that the effect of chipping was neglected for the calculation of processed area.

After laser processing, the wafer was cleaned in an ultrasonic bath of acetone followed by a bath in isopropanol for 10 min each to remove the debris deposited on the surfaces. Between and after the cleaning steps the wafer was rinsed with deionized water and dried in a nitrogen stream.

The static contact angles on the fields processed with varying pitch x were measured with a commercial available drop shape analysing system (DSA 25, Krüss GmbH, Hamburg, Germany) in a cleanroom environment of ISO-class 5 at a temperature of 21 °C. The test liquid was deionized water. The diameter of the syringe needle was 0.5 mm, dosing rate was 0.16 ml/min, and dosing volume was 2 μl. The interval time before the measurement was 5 s. The ellipse-tangent fitting method was used to determine the contact angle. Three measurements were performed per field and the average was calculated.

The relation between the contact angle and the ratio of the processed area fraction fr,h can be described by means of the Wenzel model (see Eq. 1). Since just a fraction of the glass surface is structured, the surface exhibits an inhomogeneous wetting profile which can additionally be considered using a refinement of Wenzel’s model, namely the Cassie–Baxter model [36]. According to the Cassie–Baxter model, the contact angle of a liquid on an inhomogeneous solid surface can be written as the sum of the particular contact angles θi multiplied by their surface fractions fi

$$\cos \theta = \sum\nolimits_{i} {f_{i} } \cos \theta_{i} \quad {\text{with}}\quad \sum\nolimits_{i} {f_{i} } = 1.$$
(3)

It should be remarked that the model can be applied if the scale of the heterogeneity is smaller than the droplet–surface interaction area. Since our structure sizes are in the range of a few tens of microns whereas almost droplets with a small liquid volume spread on the surface due to the low contact angle of the glass surface, our modified surface complies with the models requirements. The heterogeneity is then given by laser-generated spots with ripples and holes, respectively, and residual untreated glass surface. With this consideration, the Cassie–Baxter equation can be written as:

$$\cos \theta = f_{r,h} r_{r,h} \cos \theta_{0} + f_{0} r_{0} \cos \theta_{0} .$$
(4)

With the surface fractions of the structured area, fr,h, which is given in Eq. (2), and of the pristine area, \(f_{0} = 1 - f_{r,h}\), Eq. (4) can be written as:

$$\cos \theta = \frac{{A_{r,h} }}{{A_{0} }}r_{r,h} \cos \theta_{0} + \left( {1 - \frac{{A_{r,h} }}{{A_{0} }}} \right)r_{0} \cos \theta_{0} .$$
(5)

The roughness ratio of the pristine area can be approximated to be r0 ≈ 1. The roughness ratios of the rippled circles rr or rough holes rh were obtained by fitting this equation to the measured contact angles.

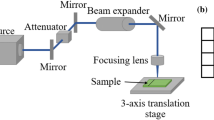
The transmission of the patterned areas was measured using the same sample. Therefore, the setup sketched in Fig. 3 was realized. It consists of a He–Ne laser as light source, an adjustable wafer holder, an iris, and a photodiode connected to a power meter. The He–Ne laser emitted light with a wavelength of 632.8 nm and a power of 2 mW. The diameter of the beam was about 2 mm, and thus significantly smaller than the widths of the structured squares. The sample was placed in a distance of 400 mm behind the beam exit. The wafer could be translated in x- and y-direction to select the area to be measured. The wafer could be also rotated around the x- and y-axis to compensate Fabry–Perot interference effects. Therefore, minimum and maximum transmissions were measured and the average was calculated. Light scattered and diffracted at the periodic pattern was blocked by an iris placed 200 mm behind the wafer. The power of the transmitted light was measured 200 mm behind the iris using a Si-photodiode (Thorlabs, S130C, Newton, NJ, United States) connected to an optical power meter (Thorlabs, PM100D, Newton, NJ, United States).

Fig. 3
figure 3

Setup for the measurement of transmission

Full size image

To determine the influence of the patterned surface on the light transmission through the wafer, the transmission T was calculated with respect to the transmission of the unprocessed surface. Therefore, T is defined as the quotient of the measured powers transmitted through a glass surface patterned with rippled spots Pr or rough holes Ph and unprocessed glass Pg. Consequently, the transmission of unprocessed glass is defined as T0 = 1. The relation between the transmission T and the processed area can be written—analogous to Eqs. (3) to (5)—as sum of the light transmitted through the processed and unprocessed area fractions, fr,h and f0, respectively:

$$T = \frac{{P_{{\text{r,h}}} }}{{P_{g} }} = f_{{\text{r,h}}} {\kern 1pt} T_{{\text{r,h}}} + f_{0} {\kern 1pt} T_{0} = \frac{{A_{{\text{r,h}}} }}{{A_{0} }}T_{{\text{r,h}}} + \left( {1 - \frac{{A_{{\text{r,h}}} }}{{A_{0} }}} \right)T_{0} ,$$
(6)

where Tr,h is the transmission of rippled spots or holes. Because both ripples and holes mainly cause scattering, the transmission can be approximated as Tr,h ≈ 0. Moreover, debris, chippings, subsurface modifications, and interference effects may influence the scattering cross section of the rippled spots or holes. Thus, a correction factor k is introduced, and the transmission was approximated as:

$$T \approx 1 - k\frac{{A_{{\text{r,h}}} }}{{A_{0} }}.$$
(7)

The correction factor was determined by fitting Eq. (7) to the measured data points.

The visual perception of the generated structures on the glass and their impact on the visual perception of an object imaged through the glass are further factors to be considered. To address these issues, an anti-fogging sample glass was fabricated using a pattern type and pitch that provided superhydrophilicity with a contact angle below 5° and the highest transmission value based on the transmission and contact angle measurements described above. The selected pattern type was the hole pattern, fluence was F = 2.6 J/cm2, N = 50 shots were applied, and pitch was x = 40 μm. This pattern was then structured on a 4″ wafer. The structured area had an oval shape with a diameter of 5–6 cm corresponding to the maximum size of the scan field. After laser structuring, the wafer was cleaned as described above. The processed wafer was then placed between a camera and object. Images were captured as the wafer was placed in the Fourier plane (Fig. 4a) and close to the object (Fig. 4b) to present the situation of a laser-structured anti-fogging surface on eyeglasses or camera cover glasses and on a showcase, respectively. For comparison, images were captured with a pristine wafer. The pictures were taken with a Canon EOS 5D camera. The lens was a Canon EF 100 mm 1:2.8 Macro USM. The object distance was 500 mm. The imaged objects were A4-sized printouts of black text on white background and a colored flower picture to investigate the impact of the generated structures on contrast and colour perception, respectively.

Fig. 4
figure 4

Optical setups for the evaluation of the visual perception of laser-generated structures on a dry glass wafer placed in the Fourier plane (a) or close to the object (b) and the imaged object itself. The visual perception of an object imaged through pristine and structured wafers in the wetted state (c) was investigated to evaluate the anti-fogging effect

Full size image

In the last experiment, the visual perception of an object behind fogged structured and unstructured glass was compared. For this purpose, a wafer was prepared, which was half structured with the parameters selected as described above, and half unstructured. The cleaning procedure was the same as for the other wafers. In the first step of the fogging experiment, the wafer was cooled below room temperature, which was between 26 and 30 °C (air humidity was between 50 and 60%), to decelerate vaporisation of the fog droplets. Therefore, the wafer was stored in a fridge with a temperature of 4 °C for about 30°min. In the next step, the glass wafer was removed from the fridge, placed about 5 cm in front of an ultrasonic humidifier (Honeywell, BH-860E), and exposed to a fog-stream at maximum power. Fogging had reached saturation already after a few seconds. The fogged wafer was then placed 5 mm above a printout with black text on white background, and a picture was taken from a distance of 25 cm with the camera described above (see Fig. 4c). It should be mentioned that camera, wafer, and object were aligned vertically for this experiment, to prevent droplets from flowing.

3 Results

The influence of the processed areas of rippled spots, fr, and holes, fh, on the water contact angle and transmission is shown in Fig. 5. Equations (5) and (7) were fitted to the measured contact angle and transmission values, respectively. The upper diagram reveals that glass surfaces become superhydrophilic if 1% of the area is patterned with holes (red region in Fig. 5) or if 10% is covered with rippled spots (grey region in Fig. 5). The lower diagram reveals that the transmission T (with respect to pristine glass) is nearly 100% for holes and about 80% for rippled spots, as glass becomes superhydrophilic.

Fig. 5
figure 5

Contact angle θ (upper diagram) and transmission T (lower diagram) of glass modified with periodic patterns of rippled spots and holes as function of the processed area fraction fr,h. The solid lines in the upper and lower diagram represent the fit curves of Eqs. (5) and (7). The red and the black dotted lines indicate the fractions of the surface that must be processed with holes and rippled circles to achieve superhydrophilicity, respectively. The red and black areas indicate the process windows to achieve superhydrophilicity with holes and both holes or ripples, respectively

Full size image

The good agreement of the fit curve with the measured contact angles indicates that the general trend including the steep decrease can be expressed according to Wenzel’s or the Cassie–Baxter model. An interesting feature, which we cannot explain at the present state, can be observed just before the steep decrease. Here, the contact angle seems to increase slightly from 25° to above 30° at around 2% before it drops below 5°. Moreover, the fit procedure returned that the roughness ratios the of rippled spots and holes are rr = 2.24 ± 0.14 and of rh = 11.3 ± 1.3, respectively. The fitted roughness ratio for the rippled spots is in excellent agreement with the roughness ratio of ripples estimated in the introduction using Eq. (2). In contrast, the fitted roughness ratio of the holes is about a factor of two higher than the estimated roughness ratio of a double hierarchal structure. Reasons for this deviation are discussed below.

The fit curves in the lower diagram of Fig. 5 are also in good agreement with the data points. The intersections of the curves with the x-axis indicate that the transmission drops to 0%, if more than 28% of the surface are patterned with holes, or more than 62% are patterned with rippled spots. Furthermore, the fit revealed that the scattering cross sections of the rippled area and the holes are a factor of kr = 1.6 ± 0.1 and kh = 3.6 ± 0.1 larger than the measured areas, respectively. Reasons for this deviation are discussed below.

The results shown in Fig. 5 were used to select the parameters to prepare a wafer for the investigation of the visual perception of structures generated on the glass and the visual perception of an object imaged through the structured glass in the dry state. We selected the holes as pattern type, because they provided superhydrophilic surfaces at higher transmission than rippled spots. Because the initial contact angles of the glass surfaces showed variations, we accepted a slight drawback in transmission and selected a pitch smaller than necessary for the investigations of visual perception. Thus, the pitch was set to 40 µm, which means that 4.9% of the area was processed. A transmission of 81% and a contact angle of 2° were measured. The laser-structured and a pristine glass wafers were placed between camera and object. Pictures of black text on white background and a colored image were taken while the wafers were located close to the object [column (a) and (b) of Fig. 6] and close to the camera objective [column (c) and (d) of Fig. 6]. First, the influence of the structured surface on the visual perception is regarded for the case that the wafer is placed closely in front of the object to be imaged [columns (a) and (b) in Fig. 6]. The structured surface is virtually invisible in the images of the text or colored picture. The enlarged images of the text illustrate the impact on optical resolution and sharpness. Comparing the insets in column (a) and (b) reveals that the text loses contrast but retains the original sharpness. Similar observations were made with the wafer closely in front of the camera objective (column (c) and (d) of Fig. 6). An increase of brightness and decrease of contrast can be identified in the images of the text and colored picture. Comparing all insets in the second row indicates that the optical resolution or sharpness is virtually independent of the location of the wafer.

Fig. 6
figure 6

Visual perception of objects imaged through unstructured (a, c) and structured (b, d) glass wafers placed close to the object (a, b) and lens (c, d) plane. The black V in (a) and (b) is the wafer holder. The dotted oval in (b) indicates the structured area

Full size image

To investigate the influence of the laser-structured surface on transmission in the wetted state, a wafer was fabricated which was half structured and half pristine. This wafer was vaporized with deionized water and photographed in front of a test structure at a distance of 25 cm between the test sample and the camera. Figure 7 shows that the word "transparency" appears blurry through wetted pristine glass (Fig. 7a), but clear through the wetted structured glass (Fig. 7b). In summary, Figs. 6 and 7 indicate that the drawback of the laser-structured surface used in this study is minimal in terms of the visual perception of objects imaged through the glass in the dry state; however, the gain in the wetted is significant.

Fig. 7
figure 7

Visual perception of a text page imaged through pristine (a) and laser-structured anti-fogging glass (b) in the wetted state

Full size image

4 Discussion

As mentioned before, the roughness ratio fitted for the rippled circles was rr = 2.24 ± 0.14, which is in excellent agreement with the value of rr = 2.24 estimated in the introduction. In contrast, the roughness ratio fitted for the holes was rh = 11.3 ± 1.3, which is about a factor of two higher than the roughness ratio of rh = 5 estimated for a double hierarchal structure in the introduction. This deviation could be related to the chippings at the hole edges occurring especially at smaller pattern periods (See Fig. 2d), debris sticking to the surface even after cleaning, or chemical surface or debris modification due to laser irradiation. Further experiments, detailed surface inspections, and improvements of the model geometry are necessary to explain the nature for the deviation of fitted and estimated roughness ratios of our periodic hole patterns. The comparison of the fitted roughness ratios further implicates that holes generate four times rougher surfaces than ripples. This also means that the area which has to be covered with holes to generate a superhydrophilic glass surface, can be four times smaller. According to our initial model that transmission depends on the area processed, this finding suggests that patterns of rough holes are the more suited pattern type to generated transparent anti-fogging surfaces.

Our model curve fitted to the transmission values measured as function of the processed area in Fig. 5 revealed that transmission drops to 0%, if 28% of the surface is patterned with holes, or if 62% are patterned with rippled spots. The results of the fit procedure revealed that the scattering cross sections of the rippled circles and the rough holes are a factor of kr = 1.6 ± 0.1 and kh = 3.6 ± 0.1 larger than the measured areas, respectively. The increased scattering cross sections could be related to debris, spatter, subsurface damage, or diffraction at the small gaps between the periodic structures. The chippings found at the edges of the holes (See Fig. 2d) could explain the larger scattering cross section compared to rippled circles. Further experiments should be carried out to explain the nature of the higher scattering cross section.

Comparing the visual perception of our generated structures with other coating or structures is difficult, because sophisticated standard test procedures have not yet been developed or are not applied. The most common method is to compare pictures taken of fogged or dewed pristine and anti-fogging glasses on top of a page with text [9, 12, 14,15,16, 37, 38]. Such a comparison is shown in Fig. 7, indicating that our anti-fogging surfaces show comparable behavior. However, detailed investigations of the visual perception of anti-fogging surfaces in the dry state are rather uncommon. Reasons could be that these surfaces are either perfectly transparent or that this issue has often been neglected. Because laser structuring typically causes scattering on optical surfaces [19, 34, 39, 40], we focused here on evaluating their visual perception in the dry state (Fig. 6). If the glass was close to an object, the structure was barely noticeable in front of a text page or a colored picture. This finding suggests that light reflected from a bright or colored object, which is transmitted through the unstructured surface, dominates light scattered at the surface structures under typical room lighting conditions. In the case that the structured glass was close to the object, the structures were only noticeable in the sense that they influenced contrast, which was only perceptible in a direct comparison with pristine wafers. Again, this was observed under typical room lighting conditions. How different lighting conditions, e.g., backlight, influence the visual perception of the structured surface could be of interest for future studies.

Regarding industrial production, throughput is an important criterion. A processing speed of about 40 mm2/min was achieved with the laser power of 0.33 W used in this study. It should be noted that the scanner system was not synchronized with the laser source. Thus, most processing time was spent for beam positioning. Neglecting the positioning time reveals that specific structuring rates of 580 mm2/min/W could be possible using a synchronized scanner. With state of the art 50 W laser sources, synchronized polygon scanners and/or parallel processing techniques, a processing time of about 34 min per m2 can be estimated from simple power scaling calculations adopting the parameters used in this study. Future studies will address power scaling and involve process optimization. This estimation suggests that the technique presented in this paper could be of interest for applications where 10 s of cm2 should be patterned. This includes, e.g., small bathroom mirrors, car mirrors or windows, diving goggles, glasses for people frequently changing environment, glasses for showcases, anti-fogging cover glasses for camera objectives, and even future applications in the fields of medicine, biology, and micro technology.

5 Conclusion

In conclusion, this paper presents two strategies to fabricate high-transparent anti-fogging glass surfaces by generating patterns of rippled circles or rough holes using an ultrashort-pulsed laser. Because laser-generated structures cause scattering, a method was developed to determine the optimal trade-off between superhydrophilic wetting behavior and visual perception of the generated structures. The results revealed that hole patterns have the potential to provide a transmission of almost 100% (relative to pristine glass), whereas rippled spots achieve about 80%, as the surface reaches the superhydrophilic state. A minimal decrease of contrast was observed in the pictures of objects imaged through a structured glass, which is a minor drawback that has to be accepted at the present state. Nevertheless, laser structuring enables direct modification of the glass, leaving room to apply additional coatings for the fabrication of multi-functional special glasses. Moreover, anti-fogging properties could be applied at locations where they are needed, e.g., at window positions close to the outlet of air conditioning systems. Thus, the fabrication of anti-fogging glasses by structuring patterns of µm-sized rough holes using ultrashort-pulsed lasers represents an interesting alternative method to coating-based techniques.