Surface instability and pattern formation by ion-induced erosion and mass redistribution

Abstract

The contribution of curvature dependent sputtering and mass redistribution to ion-induced self-organized formation of periodic surface nanopatterns is revisited. Ion incidence angle-dependent curvature coefficients and ripple wavelengths are calculated from 3-dimensional collision cascade data obtained from binary collision Monte Carlo simulations. Significant modifications concerning mass redistribution compared to the model of Carter and Vishnyakov and also models based on crater functions are introduced. Furthermore, I find that curvature-dependent erosion is the dominating contribution to pattern formation, except for very low-energy irradiation of a light matrix with heavy ions. The major modifications regarding mass redistribution and ion-induced viscous flow are related to the ion incidence angle-dependent thickness of the irradiated layer. A smaller modification concerns the relaxation of inward-directed mass redistribution. Ion-induced viscous flow in the surface layer also depends on the layer thickness and is thus strongly angle dependent. Simulation results are presented and compared to a variety of published experimental results. The simulations show that in most cases curvature-dependent erosion is the dominant contribution to surface instability and ripple pattern formation and also determines the pattern orientation transition. The simulations predict the occurrence of perpendicular ripple patterns at larger ion incidence angles, in agreement with experimental observations. Mass redistribution causes stabilization of the surface at near-normal ion incidence angles and dominates pattern formation only at very low ion energies.

1 Introduction

Ion bombardment of a solid elemental or compound surface at oblique ion incidence leads to sputter erosion as well as directed mass redistribution due to atomic recoils in the surface near region. Both effects are known to contribute to roughening and to the formation of spatially periodic ripple patterns. Pattern formation due to curvature-dependent ion beam erosion can be described by the linear theory of Bradley–Harper (BH) [1] and related theories with non-linear extensions [2–8]. In the BH model, curvature-dependent sputtering depends linearly on the locally deposited energy approximated by Sigmund’s ellipsoidal energy deposition [9]. Other continuum models which were developed to describe pattern formation on surfaces consider plastic flow in a viscoelastic continuum under ion induced stress [10–12] or hydrodynamic behaviour of an amorphous surface layer exposed to ion irradiation [13–16]. A recent experimental study on the lateral ripple propagation velocity for Si irradiated with 10 keV Xe ions reveals good agreement with the prediction by the BH model, indicating that curvature-dependent sputter erosion must play a significant role for ripple for pattern formation [17].

Pattern formation due to directed mass redistribution in the collision cascade volume parallel to the local surface was first introduced by Carter and Vishnyakov (CV) [18]. In the BH and CV theory, a gradient and curvature-dependent stochastic differential equation describes the stability (or instability) of a surface exposed to an oblique incident ion beam. According to recent publications by Madi et al. [19], Davidovitch et al. [20, 21] and Norris et al. [22], directed mass redistribution seems to be the dominating contribution to ripple pattern formation with ripple wave vectors parallel to the projected ion beam direction. Xe ion beam irradiation of amorphous carbon films in the energy regime 200 eV up to 10 keV [23] and also the analysis of ripple patterns after 5 and 10 keV ion beam irradiation of Si [24] support the contribution of mass redistribution (CV model) for parallel ripple pattern formation in the angular regime between about 45° and 70°. On the other hand, curvature-dependent sputtering (BH model) was found to determine the transition from parallel to perpendicular oriented ripples or a flat surface around angles of 75°–85° [23, 24]. In both studies, it was assumed that curvature-dependent erosion contributes according to the BH model with the assumption of Sigmund’s ellipsoidal energy deposition [1]. Here, I will show that the assumption in the BH model of a linear relation between sputtering and Sigmund’s ellipsoidal energy deposition strongly underestimates the contribution of curvature-dependent erosion. Binary collision Monte Carlo simulations provide a reliable method to calculate the lateral distribution of sputtered atom emission sites, which reveal a much stronger influence of curvature-dependent erosion to pattern formation.

Several theoretical approaches describe erosion as well as mass transport on the basis of crater functions (cf models) [22, 25–29] derived from molecular dynamics simulations. The crater function is the average height distribution h(x, y) following ion impact for a significant number of ions incident on an identical and initially flat surface with h ₀(x, y) = 0. Average height changes occur due to sputtering (removal of atoms from the target) and mass redistribution (transport of recoils atoms during the duration of collision cascade). The crater function approaches have the advantage that the lateral distribution of emission sites of sputtered atoms is treated more realistic compared to the approach in the BH model. Furthermore, the dependence of sputter erosion and atomic mass redistribution on the ion incidence angle θ is no longer based on simple sinθ approximations as used in the BH and CV model. This allows a more reliable determination of critical angles for onset of pattern formation and change of pattern orientation. For example, the CV model with the sinθ approximation for the angle-dependent forward-directed mass transport predicts a transition from stability to instability at 45° ion incidence angle. Several experimental results show that pronounced parallel oriented ripple patterns already appear at angles between 30° and 45° [30–34]. Even Carter and Vishnyakov reported pronounced parallel oriented ripple patterns after 40 keV Ar and Xe ion irradiation of Si at 45° [35].

The asymmetry of the erosive and redistributive crater functions along the projected beam direction is described by the first moments of the crater functions. These first moments can be used to replace the curvature coefficients in the BH and CV models. However, the two-dimensional projection of the 3D collision cascade into a 2D crater function neglects all depth-dependent effects such as the mean depth of the irradiated layer and inward-directed mass transport and subsequent relaxation.

In this work I discuss surface pattern formation by ion-induced atomic mass transport and curvature-dependent sputtering based on 3-dimensional collision cascade data, determined with Monte Carlo simulations using the SDTrimSP program [23, 24, 36]. From SDTrimSP I derive ion incidence angle-dependent input parameters, like the 3-dimensional recoil distribution, the 3-dimensional atomic mass transport and the lateral distribution of emission sites of sputtered atoms for a variety of ion–target combinations. These data provide the input parameters to calculate the curvature coefficients in linear continuum theories (e.g. the BH or CV theory) for different experimental conditions. The equations for the height evolution ${\text{d}}h(x,\;y,\;t)/{\text{d}}t$ of a surface, originating from atomic mass redistribution caused by ballistic displacements as well as ion beam erosion, are revisited. The calculations follow the description of Bradley and Harper [1], Carter and Vishnyakov [18] and Davidovitch et al. [20] and descriptions found in papers on crater function analyses [22, 25–29]. However, I take into account additional contributions to the height evolution in the linear expansions, which were not considered so far.

My simulation results show that curvature-dependent erosion has been underestimated in previous studies. Moreover, the decrease of the thickness of the irradiated layer with increasing ion incidence angle contributes to the stabilization of the surface in the direction parallel to the projected ion beam direction at intermediate angles and also influences the smoothing contribution due to ion-induced viscous flow. In contrast to several crater function analysis studies of pattern formation using MD simulations as input, my simulation results show that curvature-dependent erosion is not only relevant but often the dominant contribution to ion-induced pattern formation. I will also discuss the estimate of most likely ripple wavelengths.

2 Theory

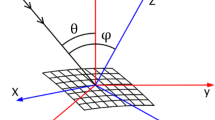
The coordinate system (u, v, w) commonly used to describe pattern formation, e.g. in the BH model [1], has the w-axis parallel to the global surface normal. The Monte Carlo simulation programs SDTrimSP and TRIDYN [36–38] use a coordinate system (x, y, z) with the x-axis pointing opposite to the surface normal and the y-axis lying in the surface typically along the projected beam direction. Here I use the system (u, v, w) = (y, −z, −x) and a system (u′, v′, w′) for the local surface (see Fig. 1), so we can retain the (x, y, z)-denotation used in the SDTrimSP output files. The computational details and the extraction of data from the SDTrimSP output files are described in the “Appendix: computational details”.

Fig. 1

a Common coordinate system used in pattern formation models. b Coordinate system used in the Monte Carlo simulation programs SDTrimSP and TRIDYN. The dashed line represents the “geometrical surface” x = w = 0, where atoms only exist for values x ≥ 0 or w ≤ 0. The dotted line in (b) represents the “interaction surface” at x = −x _C

The time evolution of a perturbation h(u, v) of a flat surface due to ion irradiation can be obtained in linear approximation as a function of the surface curvature and ion angle of incidence by [1, 6, 22],

$$ \frac{\partial h}{\partial t} = \left[ {S_{\text{u,eros}} (\theta ) + S_{\text{u,redist}} (\theta )} \right]\frac{{\partial^{2} h}}{{\partial u^{2} }} + \left[ {S_{\text{v,eros}} (\theta ) + S_{\text{v,redist}} (\theta )} \right]\frac{{\partial^{2} h}}{{\partial v^{2} }} - B^* \nabla^{4} h. $$

(1)

The angle-dependent curvature coefficients S _u and S _v consist of a sum of erosive and redistributive terms. B* is a coefficient describing surface diffusion or viscous elastic flow, leading to a relaxation towards a smooth surface. B* is often assumed as constant. Depending on the materials’ properties and the relaxation processes (e.g. viscous flow or surface diffusion) [39, 40] we should replace Eq. 1 by

$$ \frac{\partial h(u,v)}{\partial t} = S_{u} (\theta )\frac{{\partial^{2} h}}{{\partial u^{2} }} + S_{v} (\theta )\frac{{\partial^{2} h}}{{\partial v^{2} }} - F_{\text{S,rad}} d^{3} \nabla^{4} h - B\left( T \right)\nabla^{4} h. $$

(2)

Here, F _S,rad describes surface-contained radiation-induced viscous flow [41] in a thin surface layer of thickness d, and $B\left( T \right) = D_{\text{S}} \gamma \,\nu /n^{2} k_{\text{B}} T\;B\left( T \right)$ thermally activated surface diffusion, with surface diffusivity D _S, surface free energy per unit area γ and areal density ν of diffusing atoms [1]. Typically, B (at room temperature) can be neglected so that ion-induced viscous flow is the main contribution to relaxation. Preferential ion erosion, which appears as an ion-induced effective surface diffusion was introduced by Makeev et al. [5] as a further smoothing mechanism. Defect diffusion and related mechanisms leading to surface smoothing were discussed in detail by Chan et al. [6].

For a given surface viscosity η _S and surface free energy per unit area γ we get $F_{\text{S,rad}} \text{ = }\gamma \cdot J/3\eta_{\text{S,rad}}$ [39, 41], where J is the ion flux and η _S,rad is a material specific and ion-dependent radiation-induced viscosity [42]. For an ion flux J, measured in a plane perpendicular to the beam and ions with energy E _ion incident at an angle θ we have to use

$$ F_{\text{S,rad}} \left( {\theta ,E_{\text{ion}} } \right)\text{ = }\frac{\gamma \cdot J \cdot \cos \theta }{{3\eta_{\text{S,rad}} \left( {\theta ,E_{\text{ion}} } \right)}}. $$

(3)

In the literature, it is often assumed that the ion-irradiated layer has a constant thickness d (independent of the angle of incidence) and F _S,rad·d ³ is assumed to be constant [22, 43]. However, the thickness d of an ion-irradiated layer depends on ion energy and ion incidence angle and the correct dependence F _S,rad (θ, E _ion)·d(θ)³ should be used. Davidovitch et al. [20, 21] already introduced an angle-dependent relaxation coefficient $\hat{B} = \left( {1 + b^{2} } \right)^{ - 3/2} B$, with $b = \tan^{ - 1} \theta$, leading to $\hat{B} = B\cos^{3} \theta$. However, such dependence was not used later on.

For the time evolution of a Fourier component $h\left( {\vec{q},\,t} \right)$ we obtain,

$$ \left| {h\left( {\vec{q},t} \right)} \right|^{2} = \left| {h\left( {\vec{q},0} \right)} \right|^{2} \cdot e^{{R\left( {\vec{q}} \right)t}} . $$

(4)

With $R\left( {\vec{q}} \right)$ given by (Eq. 8 of Ref. [40]),

$$ R\left( {\vec{q}} \right) = - \left[ {S_{\text{u}} (\theta )q_{\text{u}}^{2} + S_{\text{v}} (\theta )q_{\text{v}}^{2} + \left( {F_{\text{S,rad}} d^{3} + B} \right)\left( {q_{\text{u}}^{2} + q_{\text{v}}^{2} } \right)^{2} } \right]. $$

(5)

Structures will grow exponentially with time for positive values of R, and thus surface instability leading to ripple formation requires negative values of S _u and S _v. The wavelength with largest R for B = 0 is

$$ \lambda_{\text{u}} (\theta ) = 2\pi \sqrt {\frac{{2\left( {F_{\text{S,rad}} \cdot d(\theta )^{3} } \right)}}{{ - S_{\text{u}} (\theta )}}} \quad {\text{and}}\quad \lambda_{\text{v}} (\theta ) = 2\pi \sqrt {\frac{{2\left( {F_{\text{S,rad}} \cdot d(\theta )^{3} } \right)}}{{ - S_{\text{v}} (\theta )}}} . $$

(6)

Positive real values of λ _u or λ _v only exist for negative coefficients S _u and S _v. Both, F _S,rad and S _u (or S _v) are proportional to the ion flux J, so that the wavelength should be independent of the ion flux. For values S _u or S _v approaching zero we expect the wavelength to diverge.

2.1 Curvature-dependent erosion

We now consider an ion flux J (defined in a plane perpendicular to the ion beam) incident at an angle θ with respect to the mean surface normal. The local surface normal exhibits a small gradient $\frac{\partial h}{\partial u}\left( {{\text{or}}\;\frac{\partial h}{\partial v}} \right)$ and the local surface normal is titled with respect to the mean surface normal by a small angle γ with $\tan \gamma \approx \gamma = \frac{\partial h}{\partial u}$. The local ion incidence angle is $\xi = \theta - \gamma = \theta - \frac{\partial h}{\partial u}$ (Fig. 2).

Fig. 2

Schematics of an ion beam incident on an inclined surface

The erosive part of the curvature-dependent height change is derived in the usual way as described by Bradley and Harper [1], but using $\delta_{\text{u,eros}} (\theta )$ from Eq. A.1, which is equivalent to the 1st moment of the erosive crater function (Eq. A.2) [26]. We obtain the results described in crater function models [22, 26, 28]:

$$ \begin{aligned} \frac{\partial h}{\partial t} &=& - \frac{J}{n} \cdot \left( {\left( {\frac{dY}{d\theta }\delta_{\text{u,eros}} + Y\frac{{d\delta_{\text{u,eros}} }}{d\theta }} \right) \cdot \cos \theta - Y \cdot \delta_{\text{u,eros}} \cdot \sin \theta } \right)\frac{{\partial^{2} h}}{{\partial u^{2} }} \hfill \\ \frac{\partial h}{\partial t} &=& + J \cdot \left( {\frac{{dM_{\text{eros}}^{(1)} }}{d\theta } \cdot \cos \theta - M_{\text{eros}}^{(1)} \cdot \sin \theta } \right) \cdot \frac{{\partial^{2} h}}{{\partial u^{2} }}. \hfill \\ \end{aligned} $$

(7)

$$ \begin{gathered} \frac{\partial h}{\partial t} = - \frac{J}{n} \cdot Y \cdot \delta_{\text{u,eros}} (\theta ) \cdot \cos \theta \cdot \cot \theta \cdot \frac{{\partial^{2} h}}{{\partial {\text{v}}^{2} }} \hfill \\ \frac{\partial h}{\partial t} = + J \cdot M_{\text{eros}}^{(1)} \cdot \cos \theta \cdot \cot \theta \cdot \frac{{\partial^{2} h}}{{\partial {\text{v}}^{2} }}. \hfill \\ \end{gathered} $$

(8)

In the BH model [1] with coefficient Γ₁ < 0 for small angles and Γ₂ < 0 the curvature-dependent contribution is given by

$$ \frac{\partial h}{\partial t} = + \frac{J}{n} \cdot Y \cdot a \cdot \varGamma_{1} (\theta )\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(9)

$$ \frac{\partial h}{\partial t} = + \frac{J}{n} \cdot Y \cdot a \cdot \varGamma_{2} (\theta ) \cdot \frac{{\partial^{2} h}}{{\partial {\text{v}}^{2} }}. $$

(10)

2.2 Ion-induced mass redistribution including the layer thickness dependence

The collision cascades caused by the incident ions generate a net atomic mass transport. For an ion incidence angle θ, the forward directed mass transport distances per ion is δ_u(θ) given by Eq. A.5. Let us first consider the forward directed atomic flux $F\left( {\vec{s}} \right)$ along a direction $\vec{s}$ parallel to the local surface, inclined by a small angle γ with respect to the mean surface and for an ion incidence angle θ. $\delta_{u} \left( {\theta - \gamma } \right)$ given by Eq. A.5 is the component of the mean transport distance per ion parallel to the local surface, and $D\left( {\theta - \gamma } \right)$ is a mean depth measured from the surface in which the atomic transport takes place. This mean depth $D\left( {\theta - \gamma } \right)$ is not directly related to the ion range, because ion range and recoil depth distribution may differ significantly, depending on ion energy and ion and target atomic masses. Instead, $D\left( {\theta - \gamma } \right)$ is calculated as mean depth of the recoil distribution as given by Eq. A.4. The strong decrease of D with increasing θ is obvious from Fig. 3, showing the recoil depth distribution and D(θ) calculated for 10 keV Xe incident on Si. D(θ) does not follow a simple $\cos \theta$ behaviour but can be approximated by $D(\theta ) \approx D_{0} + D_{1} \cos (\alpha \theta )$, as indicated in Fig. 3b. D(θ) does not approach zero at large angles because it is dominated by inward mass transport caused by inelastic reflected ions. The dependence of the thickness of the irradiated layer on the ion incidence angle is also nicely seen in cross-sectional TEM images of Ar-irradiated Si (Ref. [44] or Fig. 22 of Ref. [6]).

Fig. 3

a Depth distribution of recoil end positions calculated with SDTrimSP, and b average depth of recoils (Eq. A.4) as a function of the ion incidence angle. The dashed curve indicates a cosθ dependence, the solid curve is a fit using the formula shown in the figure

For a target atomic density n and surface area A, there are $n \cdot A \cdot D$ atoms in a surface layer with mean thickness D. Later on we will see that we are free how to define D because only the relative angular derivative ${{(1/D)\partial D} \mathord{\left/ {\vphantom {{(1/D)\partial D} {\partial \theta }}} \right. \kern-0pt} {\partial \theta }}$ remains. The mass transport parallel to the local surface due to numerous recoils in a collision cascade is expressed as mean transport distance $\delta_{\text{u}}$ of a single atom per incident ion [18]. For a given incident ion fluence Φ and ion flux $J \cdot \cos \left( {\theta - \gamma } \right) = \frac{{{\text{d}}\varPhi }}{{{\text{d}}t}} \cdot \cos \left( {\theta - \gamma } \right)$, the rate at which target atoms are displaced by a mean distance $\delta_{\text{u}}$ is $J \cdot A \cdot \cos (\theta - \gamma )$. The average drift velocity v _drift of the whole surface layer volume A·D with mean thickness D is, therefore,

$$ v_{\text{drift}} = \frac{J}{n}\frac{{\delta_{\text{u}} \left( {\theta - \gamma } \right)}}{{D\left( {\theta - \gamma } \right)}} \cdot \cos \left( {\theta - \gamma } \right). $$

(11)

The atomic flux along direction $\vec{s}$ parallel to the local surface is then given by

$$ F\left( {\vec{s},\theta ,\gamma } \right) = v_{\text{drift}} \cdot n = J \cdot \cos (\theta - \gamma ) \cdot \frac{{\delta_{\text{u}} \left( {\theta - \gamma } \right)}}{{D\left( {\theta - \gamma } \right)}}. $$

(12)

In the CV model, the mean depth D(θ − γ) is ignored (or is assumed to be constant and independent of the ion incidence angle) and the atomic flux is given with unusual dimension (m⁻¹s⁻¹) as $F\left( {\vec{s}} \right) = J \cdot \cos (\theta - \gamma ) \cdot \delta_{\text{u}} (\theta - \gamma )$ [18].

Assuming that relaxation processes ensure a constant atomic density of the target (incompressibility) the continuity condition at the surface h(u, t) is given according to Oron et al. (Eq. 2.2.c) [45] with local velocities v _w (u, w) and v _u(u, w) along w- and u-direction.

$$ \frac{{\partial v_{\text{w}} }}{\partial w} = - \frac{{\partial v_{\text{u}} }}{\partial u}. $$

(13)

The kinematic boundary condition at the surface for the Navier–Stokes equations of a thin viscous film of local thickness h(u, t) bound to a solid substrate is given by Eq. 2.12a of Ref. [45]:

$$ \frac{\partial h}{\partial t} = v_{\text{W}} - v_{\text{u}} \frac{\partial h}{\partial u} $$

(14)

As boundary condition at the interface to the solid substrate we choose no slip (v _u = 0) and no transfer (v _w = 0).

Now, in our case, the thickness D of the irradiated surface layer depends on the ion incidence angle θ as described above. This is illustrated in Fig. 4 for an ion-irradiated viscous surface layer on a non-irradiated solid substrate (in analogy to Fig. 7 of Ref. [45] for a bounded viscous film). We obtain in linear expansion

Fig. 4

Sketch of an ion-irradiated viscous surface layer on a non-irradiated solid substrate. The thickness h ₀ = D(θ) for a flat layer irradiated with ions (thick arrows) incident at angle θ is shown as dot-dashed line, with average layer thickness D(θ) defined by Eq. A.4. The upper curve is the height profile h(u, t) of a rippled surface. The lower curve is the interface h(u, t)–D(u, t) between irradiated an no-irradiated solid. The vertical arrows indicate the positions, where the layer thickness is equal to the thickness D(θ) of a flat irradiated layer. In between these positions D(θ) is either larger or smaller compared to D(θ) because the local ion incidence angle is either θ − γ or θ + γ

$$ D(\theta - \gamma ) = D(\theta ) - \left. {\frac{\partial D(\theta - \gamma )}{\partial (\theta - \gamma )}} \right|_{\gamma = 0} \cdot \gamma = D(\theta ) - \left. {\frac{\partial D(\theta - \gamma )}{\partial (\theta - \gamma )}} \right|_{\gamma = 0} \cdot \frac{\partial h}{\partial u}. $$

(15)

Note that the negative sign in Eq. 15 occurs because of the definition of γ. For a given curvature $\frac{{\partial^{2} h}}{{\partial u^{2} }}$ of the surface the derivative $\frac{\partial D}{\partial u}$ is then given by,

$$ \frac{\partial D}{\partial u} = - \frac{\partial D}{\partial \theta }\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(16)

Since $\frac{\partial D}{\partial \theta } < 0$, the layer thickness D increases with increasing u in case of a positive curvature and decreases in case of a negative curvature in accordance with the experimental observations (Ref. [44] or Fig. 22 of Ref. [6]).

The kinematic boundary condition (Eq.14) must be replaced by

$$ \frac{\partial h}{\partial t} = v_{\text{w}} - v_{\text{u}} \cdot \left( {\frac{\partial h}{\partial u} - \frac{\partial D}{\partial u}} \right) = v_{\text{w}} - v_{\text{u}} \cdot \left( {\frac{\partial h}{\partial u} + \frac{\partial D}{\partial \theta }\frac{{\partial^{2} h}}{{\partial u^{2} }}} \right), $$

(17)

where we have subtracted the height variation $\frac{\partial D}{\partial u}$ due to the angle-dependent layer thickness D(θ) from the total height variation $\frac{\partial h}{\partial u}$.

Combining Eqs. 17 and 13 we obtain for the rate of local height variation $\frac{\partial h}{\partial \,t}$ due to ion induced mass transport

$$ \frac{\partial h}{\partial t} = - \int\limits_{h - D}^{h} {\frac{{\partial v_{\text{u}} }}{\partial u}} {\text{d}}w - v_{\text{u}} \cdot \frac{\partial h}{\partial u} - \frac{\partial D}{\partial \theta }\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(18)

The integration limits are determined by the local thickness D of the irradiated layer.

We can combine the first two terms using the interface boundary conditions and integration in parts to obtain

$$ \frac{\partial h}{\partial t} = - \frac{\partial }{{\partial_{\text{u}} }}\int\limits_{h - D}^{h} {v_{\text{u}} } {\text{d}}w - v_{\text{u}} \cdot \frac{\partial D}{\partial \theta }\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(19)

The integral over a velocity profile v _u(w) within the layer D is simply the average drift velocity v _drift from Eq. 11 multiplied by the layer thickness D

$$ \int\limits_{h - D}^{h} {v_{\text{u}} } {\text{d}}w = v_{\text{drift}} \cdot D. $$

(20)

We then obtain

$$ \frac{\partial h}{\partial t} = - \frac{J}{n}\frac{\partial }{\partial u}\left( {\delta_{\text{u}} (\theta ) \cdot \cos (\theta )} \right) - \frac{J}{n}\cos \theta \frac{{\delta_{\text{u}} (\theta )}}{D(\theta )}\frac{\partial D(\theta )}{\partial (\theta )}\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(21)

For the linear expansion of the first term we get in analogy to Eq. 16

$$ \frac{\partial }{\partial u}\left( {\delta_{\text{u}} (\theta ) \cdot \cos (\theta )} \right) = - \left( { - \sin \theta \cdot \delta_{\text{u}} (\theta ) + \cos (\theta )\frac{{\partial \delta_{\text{u}} }}{\partial \theta }} \right)\frac{{\partial^{2} h}}{{\partial u^{2} }} $$

(22)

Note that the negative sign before the brackets in Eq. 22 occurs because of the definition of γ. Inserting Eq. 22 in Eq. 21 finally yields curvature dependence due to mass redistribution for an ion-irradiated layer on a non-irradiated solid and a curvature in u-direction.

$$ \frac{\partial h}{\partial t} = + \frac{J}{n}\left[ { - \delta_{\text{u}} (\theta ) \cdot \sin \theta + \cos (\theta )\left( {\frac{{\partial \delta_{\text{u}} }}{\partial \theta } - \frac{{\delta_{\text{u}} (\theta )}}{D(\theta )}\frac{\partial D(\theta )}{\partial (\theta )}} \right)} \right]\frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(23)

Equation 23 is directly obtained from the spatial derivative of the first-order expansion around θ of $F\left( {\vec{s},\theta ,\gamma } \right)$. The corresponding relation for the v-direction does not contain a thickness-dependent term because the thickness variation only arises along u-direction (Eq. 16). I can, therefore, use the relation derived in the crater function models [22, 26, 28],

$$ \frac{\partial h}{\partial t} = + \frac{J}{n}\delta_{\text{u}} (\theta )\cos (\theta ) \cdot \cot \theta \frac{{\partial^{2} h}}{{\partial v^{2} }}. $$

(24)

As expected for a bounded thin viscous film, the mean thickness of the layer D(θ) cancels out. However, for an ion-irradiated film the relative angular variation $\frac{1}{D(\theta )} \cdot \frac{\partial D(\theta )}{\partial \theta }$ is non-zero due to the modified kinematic boundary condition (Eq. 17). The angle dependence of the irradiated layer thickness D(θ) leads to a stabilizing contribution in u-direction, which is most pronounced when the slope $\frac{\partial D(\theta )}{\partial \theta }$ is maximum (see. Fig. 3b). This is in particular the case for intermediate angles.

2.3 The contribution of relaxation of inward-directed mass transport

Up to now we have used several average quantities to determine the curvature coefficients, such as the sputter yield Y atoms per ion, the number N _D of displacements per ion, the average depth D of the irradiated layer and the lateral mass transport distance δ_u per ion. Also the moments of the crater function are average values and even the crater functions itself are average functions obtained for a large number of simulated ion impacts.

On average quantity not considered so far is the inward mass transport distance ${-}\delta_{\text{w}}$ per ion as defined in Eq. A.10. It is usually assumed that inward mass transport relaxes completely to maintain a constant density. Therefore, it has no effect on the pattern formation and can be neglected.

Let us make a Gedankenexperiment and consider a flat surface and an ion fluence $\varPhi = n^{2/3}$ incident in normal direction on a solid with atomic density n. The fluence is chosen so there is one incident ion per surface atom. The ion fluence causes an average inward transport with distance −δ_w per ion. We are free to choose which target atom underneath the surface is displaced in this way, so I select a surface atom. For fluence $\varPhi = n^{2/3}$an atomic surface layer is displaced inward by −δ_w and then relaxes back to the surface by distance +δ_w. However, in the meantime the surface is eroded with average sputter yield Y atoms per ion, corresponding to an erosion depth $\left( {n^{2/3} Y} \right)/n = Y/n^{1/3}$. The average backward relaxation distance per ion is, therefore, a little bit smaller and given by $\delta_{\text{w}} - Y/n^{1/3}$. We see that we can directly compare this erosion depth $Y/n^{1/3}$with the average mass transport distances per ion (Eqs. A.5, A.10) or first redistributive moments of a crater function (Eq. A.6) introduced in the CV model [18] and crater function models [26].

Now we consider a rippled surface and ions incident at angle θ with respect to the global surface normal (Fig. 5). The surface is eroded with average rate $\upsilon_{0} (\theta ) = (J/n) \cdot Y(\theta ) \cdot \cos (\theta )$ [1] and for fluence $\varPhi \cdot \cos \theta = n^{2/3}$ the surface is shifted downwards by the average erosion depth $Y/n^{1/3}$. In Fig. 5 the arrows indicate the mass transport of an imaginary surface atomic layer displaced by an ion fluence $\varPhi \cdot \cos \theta = n^{2/3}$. At ion impact position A in Fig. 5 with incidence angle θ the inward mass transport relaxes back to the same u _A position. For the ion impact point B in Fig. 5 with positive slope the mass transport proceeds inward $- \delta_{{{\text{w}}\prime }}$ and forward $+ \delta_{{{\text{u}}\prime }}$ and relaxes back towards a new position given by u = u _B +(Y/n ^1/3)∙γ with $\gamma = {{\partial h} \mathord{\left/ {\vphantom {{\partial h} {\partial u}}} \right. \kern-0pt} {\partial u}}$. The forward mass transport distance $\delta_{u}$ is then modified to $\delta_{\text{u}} + \left( {Y/n^{1/3} } \right) \cdot \gamma$. For the ion impact point C in Fig. 5 with negative slope and the relaxation occurs towards position $u = u_{\text{C}} - \left( {Y/n^{1/3} } \right) \cdot \left| \gamma \right|$ and δ _u is modified to $\delta_{\text{u}} - \left( {Y/n^{1/3} } \right) \cdot \left| \gamma \right|$. We, therefore, have to add a term to Eq. 22 given by

Fig. 5

Sketch of ion induced mass transport in a film with atomic density n for an ion fluence Φ·cosθ = n ^2/3, where the average mass transport distances δ_u and δ_w per ion are directly comparable to the average erosion depth Y/n ^1/3. A ion impact position where mass redistribution relaxes to the same u-position. B ion impact position on the surface with positive slope leading to forward shifted mass relaxation. C ion impact position on the surface with negative slope leading to backward shifted mass relaxation. The long thick arrows indicate the ion beam incident at angle θ with respect to the global surface normal. The short thick arrows indicate the shift of distance Y/n ^1/3·γ

$$ \frac{\partial }{\partial u}\left( {\frac{Y}{{n^{1/3} }} \cdot \frac{\partial h}{\partial u} \cdot \cos (\theta )} \right) \approx \cos \theta \frac{Y}{{n^{1/3} }} \cdot \frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(25)

In analogy we find for perpendicular ripples

$$ \frac{\partial }{\partial v}\left( {\frac{Y}{{n^{1/3} }} \cdot \frac{\partial h}{\partial v} \cdot \cos (\theta )} \right) \approx \cos \theta \frac{Y}{{n^{1/3} }} \cdot \frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(26)

The right sides of Eqs. 25 and 26 are the linear terms in the expansion around θ.

Inserting this into Eqs. 23 and 24 we obtain

$$ \frac{\partial h}{\partial t} = + \frac{J}{n}\left[ { - \delta_{\text{u}} (\theta ) \cdot \sin \theta + \cos (\theta )\left( {\frac{{\partial \delta_{u} }}{\partial \theta } - \frac{Y}{{n^{1/3} }} - \frac{{\delta_{\text{u}} (\theta )}}{D(\theta )}\frac{\partial D(\theta )}{\partial (\theta )}} \right)} \right]\frac{{\partial^{2} h}}{{\partial u^{2} }} $$

(27)

$$ \frac{\partial h}{\partial t} = + \frac{J}{n}\delta_{\text{u}} (\theta )\cos (\theta ) \cdot \left( {\cot \theta - \frac{Y}{{n^{1/3} }}} \right)\frac{{\partial^{2} h}}{{\partial v^{2} }}. $$

(28)

The additional correction $Y(\theta ) \cdot n^{ - 1/3}$ seems to be small, but Y reaches a maximum at larger angles while cotθ approaches zero. Therefore, the correction term reduces the small stabilizing contribution of mass redistribution at large ion incidence angles. Eventually, the negative term in Eq. 8 from curvature-dependent erosion overcompensates the term in Eq. 28 and a surface instability occurs, leading to the formation of perpendicular ripple patterns.

2.4 The curvature coefficients S _u and S _v

In the CV model [18] and also in crater function (cf) models [22, 25–29] the last two terms in the inner bracket of Eq. 27 and the last term in Eq. 28 disappear because (1) D(θ) is assumed constant and (2) the relaxation of inward mass redistribution on a rippled surface is not considered. Without these two terms I obtain exactly the result of the cf models [22, 26, 28] and using $\delta_{\text{u}} \approx \delta_{0} \sin \theta$ with δ₀ given by Eq. A.9, the result of the CV model [18, 20] for a curvature in u- and v-direction, respectively,

$$ \left. {\frac{\partial h}{\partial t}} \right|_{\text{cf}} = \frac{J}{n}\left[ { - \delta_{\text{u}} (\theta ) \cdot \sin \theta + \frac{{\partial \delta_{u} (\theta )}}{\partial (\theta )}\cos \theta } \right] \cdot \frac{{\partial^{2} h}}{{\partial u^{2} }}\ ;\quad \left. {\frac{\partial h}{\partial t}} \right|_{\text{CV}} = \frac{J}{n}\delta_{0} \cos 2\theta \cdot \frac{{\partial^{2} h}}{{\partial u^{2} }}. $$

(29)

$$ \left. {\frac{\partial h}{\partial t}} \right|_{\text{cf}} = \frac{J}{n} \cdot \delta_{\text{u}} (\theta ) \cdot \cot \theta \cos \theta \frac{{\partial^{2} h}}{{\partial v^{2} }} ;\quad \left. {\frac{\partial h}{\partial t}} \right|_{\text{CV}} = \frac{J}{n} \cdot \delta_{0} \cdot \cos^{2} \theta \frac{{\partial^{2} h}}{{\partial v^{2} }}. $$

(30)

In the following section I present selected simulation results and compare the different model assumptions made in the BH + CV model, the carter function model and the extensions introduced here. I calculate the curvature coefficients S _u and S _v defined by Eqs. 1 and 2 for the different models. A surface instability occurs if either $S_{\text{u,eros}} + S_{\text{u,redist}}$ or $S_{\text{v,eros}} + S_{\text{v,redist}}$ becomes negative. For the BH + CV model I use Eqs. 9, 10, 29 and 30 and obtain the curvature coefficients as derived in [1] and [18]:

$$ \begin{gathered} S_{\text{u,BH + CV}} = \frac{J}{n} \cdot \left[ {Y \cdot a \cdot \varGamma_{1} + \delta_{0} \cdot \cos 2\theta } \right] \hfill \\ S_{\text{v,BH + CV}} = \frac{J}{n} \cdot \left[ {Y \cdot a \cdot \varGamma_{2} + \delta_{0} \cdot \cos^{2} \theta } \right] \hfill \\ \end{gathered} $$

(31)

For the crater function model (cf model) I use Eqs. 7, 8, i.e. the same curvature coefficients as derived in [22, 26, 28],

$$ \begin{gathered} S_{\text{u,cf}} = \frac{J}{n} \cdot \left[ {\frac{{d\left( {Y\delta_{\text{u,eros}} \cos \theta + \delta_{\text{u}} \cos \theta } \right)}}{d\theta }} \right] \hfill \\ S_{\text{v,cf}} = \frac{J}{n} \cdot \cos \theta \cdot \cot \theta \cdot \left[ { - Y \cdot \delta_{\text{u,eros}} + \delta_{\text{u}} } \right]. \hfill \\ \end{gathered} $$

(32)

Finally, including the extensions introduced here with the HH model, I obtain with Eqs. 7, 8, 27 and 28 the curvature coefficients

$$ \begin{gathered} S_{\text{u,HH}} = S_{\text{u,cf}} - \frac{J}{n}\cos \theta \cdot \left( {\frac{{\delta_{\text{u}} }}{D} \cdot \frac{\partial D}{\partial \theta } + \frac{Y}{{n^{1/3} }}} \right) \hfill \\ S_{\text{v,HH}} = S_{\text{v,cf}} - \frac{J}{n}\cos \theta \cdot \frac{Y}{{n^{1/3} }}. \hfill \\ \end{gathered} $$

(33)

3 Results

In this chapter I present selected calculations of coefficients S _u and S _v, predictions of ripple wavelengths. For these calculations I have chosen an ion flux J = 1 × 10¹² ions/cm²/s. Scaling to S _u and S _v coefficients shown in other publications is only made through this reference flux. The relevant input parameters, which were calculated with SDTrimSP, are listed in Table 1. Curvature coefficients were also calculated for several other ion-target combinations, such as, 250 eV–2 keV Ar on a-SiO₂, 250–1,500 eV Xe on Si, 1–2 keV Kr and Xe on Ge, 30 keV Ga on SiO₂ and 650 eV Ar on Au, which will be presented in future publications or can be made available on request.

Table 1 Parameters calculated with SDTrimSP for different ion-target combinations and ion incidence angles between 0° and 85°

3.1 Simulations for 250 eV Ar on Si

This ion-target combination was studied experimentally by [46] and also investigated using MD simulations and crater function analyses [22]. It is, therefore, suited to compare my calculations using Monte Carlo simulations with the carter function analysis based on MD simulations. Experimentally, parallel ripple patterns with wavelength decreasing from about 50–20 nm were observed in the angular regime 50°–75° [46]. Perpendicular mode ripples with short wavelength around 25 nm were observed at an ion incidence angle of 85°.

The coefficients S _u and S _v calculated for the three different models are plotted in Fig. 6. The analysis according to BH + CV model predicts an instability in u-direction above 45°, no orientation transition (parallel → perpendicular or parallel → flat) and no instability in v-direction. Mass redistribution appears as dominating contribution. The crater function analysis (cf) already reveals a significant contribution of both erosion and mass redistribution. Instability in u-direction parallel oriented ripples should occur between about 30° and 80°. S _v remains always positive so that no perpendicular ripples are predicted, similar to the result of Ref. [22]. In the analysis using the HH model, however, instability in v-direction occurs for angles above about 70° in agreement with the experiment [46]. This instability is eventually caused by the new relaxation term $\sim Y/n^{1/3}$. The angular regime for parallel ripples is reduced to about 40°–80°. Shifting the impact point from (−x _c, 0, 0) to (0, x _c·tanθ, 0) significantly reduces the coefficient for curvature-dependent erosion, and parallel ripples are predicted up to about 85°, which is not in accordance with the experimental observation [46]. The respective curvature coefficients are plotted as dot-dashed line and open symbols in Fig. 6.

Fig. 6

Curvature coefficients S _u and S _v for 250 eV Ar on Si as function of ion incidence angle, calculated according to the CV and BH model, the crater function (cf) model and the HH model for ion flux J = 1 × 10¹² ions/cm². Full circles total S _u coefficients, full triangles total S _v coefficients, thick solid lines erosive component of S _u; dashed lines redistributive component of S _u. The open circles [data set S _u cf (0)] and the dot-dashed line [data set S _u,eros (0)] are obtained by shifting the ion impact point from (−x _c, 0, 0) to (0, x _c·tanθ, 0) as discussed in the “Appendix: computational details”

Evaluating the difference between my calculations and the ones of Ref. [22] it turns out that the sputter yield obtained from MD simulations is comparable to the SDTrimSP values. The maximum value of the 1st moment $M_{\text{redist}}^{(1)}$of the redistribution crater function shown in Ref. [22] is about +12.5 × 10⁻² nm⁴ per ion at 45°. I obtain with Table 1 and Eq. A.6 a somewhat smaller maximum value of 8.1 × 10⁻² nm⁴ per ion. Also the maximum of $M_{\text{redist}}^{(1)}$determined from SDTrimSP is around 55° The minimum of the 1st moment of the erosive crater function shown in Ref. [22] is about −1.8 × 10⁻² nm⁴ per ion at 65°. I obtain with Table 1 and Eq. A.2 a three times larger value of −5.2 × 10⁻² nm⁴ per ion at 65°, which is, however, reduced to −2.5 × 10⁻² nm⁴ per ion if the impact point is set to the geometrical surface.

3.2 Simulations for 500 eV Ar on a-SiO₂

This ion-target combination was experimentally studied by Keller et al. [47] so that a comparison with experimental results can be made. Up to about 30° incidence angles the surface remains flat. Parallel ripples are observed for angles of 45° and 52° with wavelength between 20 and 35 nm. At 72° a perpendicular oriented pattern occurs with a periodicity of about 100 nm.

The SDTrimSP calculation was done for the density of silica (ρ ≈ 2.3 g/cm³) and using the dynamic mode, which takes care of stoichiometry changes due to preferential sputtering. The calculated erosion and redistribution crater functions for three different angles of incidence are plotted in Fig. 7. The crater functions visualize the lateral extension of the collision cascade and indicate the emission sites of sputtered atoms. It is also obvious that the centre of the collision cascade shifts away from ion impact point with increasing angle of incidence as discussed in the “Appendix: computational details”. The only quantity which can approximately be extracted graphically is the mean distance δ_u,eros (Eq. A.1) related to the 1st moment of the erosion crater function.

Fig. 7

Redistribution (left) and erosion (right) crater functions for 500 eV Ar ions incident on a-SiO₂ for angles 20°, 60° and 80°. N _D is the number of displacements per ion and Y the sputter yield. δ_u,eros (Eq. A.1) can be estimated from the plot (arrows). δ_u,redist (Eq. A.5) is the mean distance per ion and cannot be estimated graphically

The coefficients S _u and S _v calculated for the three different models are plotted in Fig. 8. The analysis according to BH + CV model predicts an instability in u-direction above 45°, no orientation transition (parallel → perpendicular or parallel → flat) and no instability in v-direction. Mass redistribution appears as dominating contribution. The analysis based on crater functions (cf) reveals a significant contribution of both erosion and redistribution. Instability in u-direction occurs between about 30° and 70°, leading to the formation of parallel oriented ripples. Above about 60° S _v becomes slightly negative, so the surface is instable in v-direction, leading to perpendicular ripples. The analysis using the HH model is similar; however, the instability in v-direction is more pronounced and the angular regime for parallel ripples is reduced to about 35°–68°. Shifting the impact point from (−x _c, 0, 0) to (0, x _c·tanθ, 0) reduces the coefficient for curvature-dependent erosion and parallel ripples are predicted up to about 85°, which is not in accordance with the experimental observation [47, 48]. The respective curvature coefficients are plotted in Fig. 8 as dot-dashed line and open symbols.

Fig. 8

Curvature coefficients S _u and S _v for 500 eV Ar on a-SiO₂ as function of ion incidence angle calculated according to the CV and BH model, the crater function (cf) model and the HH model for ion flux J = 1 × 10¹² ions/cm². Full circles total S _u coefficients, full triangles total S _v coefficients, thick solid lines erosive component of S _u; dashed lines redistributive component of S _u. The open circles [data set S _u cf (0)] and the dot-dashed line [data set S _u,eros (0)] are obtained by shifting the ion impact point from (−x _c, 0, 0) to (0, x _c·tanθ, 0) as discussed in the “Appendix: computational details”

3.3 Simulations for 1 keV Ar on Si

The case 1 keV Ar on Si was already studied experimentally by several groups [19, 46, 49–51]. Parallel ripples occur within angles of 50°–70°, and perpendicular ripples occur at about 75°. An angular regime between about 60°–70° seems to exist where both parallel and perpendicular ripples coexist. Curvature coefficients were measured using small-angle X-ray scattering (although with the assumption of a constant and angle-independent parameter B* in Eq. 1) and also estimated using the CV model [19]. This study reports a dominating contribution of mass transport, whereas curvature-dependent erosion seems to be almost negligible. Our own previous calculations using curvature coefficients for mass redistribution from SDTrimSP and curvature-dependent erosion according to the BH model revealed that the transition region between parallel and perpendicular ripples is determined by curvature-dependent erosion [23].

The coefficients S _u and S _v calculated for the three different models are plotted in Fig. 9. The analysis according to the BH + CV model predicts instability in u-direction above 45°. Mass redistribution appears as dominating contribution. The analysis based on crater functions (cf) reveals a significant contribution of both erosion and redistribution. Instability in u-direction, leading to parallel ripples, occurs between about 30° and 70°. Perpendicular ripples should be generated above about 50°. The analysis using the HH model is similar; however, the instability in v-direction is more pronounced and the angular regime for parallel ripples is reduced to about 35°–70°. There is an angular regime where ripples with both orientations will be superimposed, which is in agreement with experimental observations [19, 46, 49–51]. The choice of the ion impact point has a minor influence on the coefficients.

Fig. 9

Curvature coefficients S _u and S _v for 1 keV Ar on Si, calculated according to the CV and BH model, the cf-model and the HH model. Solid circles total S _u coefficient, solid triangles total S _v coefficient, thick solid lines erosive contribution to S _u, dashed lines redistributive contribution to S _u. The open circles [data set S _u cf (0)] and the dot-dashed line [data set S _u,_eros (0)] are obtained by shifting the ion impact point from (−x _c, 0, 0) to (0, x _c·tanθ, 0) as discussed in the “Appendix: computational details”

3.4 Simulations for 10–40 keV Xe ions on Si

Our previous experiments for 5 and 10 keV Xe ion irradiation of Si show pronounced parallel ripples at intermediate angles of about 50°–75°, a transition region around 80° and weak perpendicular ripples at 85° [24, 71, 72]. The corresponding calculations of the curvature coefficients for the 10 keV on Si case are shown in Fig. 10. I have also calculated the case for 40 keV Xe ions because it was the experimental motivation for Carter and Vishnyakov to develop the mass redistribution model to explain stability or instability of a surface against ion irradiation. The corresponding curvature coefficients are shown in Fig. 11. The cf- and HH-model clearly reveal curvature-dependent erosion as the dominant effect for pattern formation. Mass redistribution only determines the stability of the surface at smaller angles. The onset of the instability regime for 40 keV Xe is at about 40° (in agreement with the experiment [18]).

Fig. 10

Curvature coefficients for 10 keV Xe on Si, calculated according to the CV + BH model, the cf-model and the HH model. Solid circles total S _u coefficient, solid triangles total S _v coefficient, thick solid lines erosive contribution to S _u, dashed lines redistributive contribution to S _u. Open symbols see figure captions of Figs. 8 and 9

Fig. 11

Curvature coefficients for 40 keV Xe on Si, calculated according to the CV and BH model, the cf-model and the HH model. Solid circles total S _u coefficient, solid triangles total S _v coefficient, thick solid lines erosive contribution to S _u, dashed lines redistributive contribution to S _u

Interestingly, the combined BH + CV model predicts rather well the angular regime for parallel ripples. This is because curvature-dependent erosion is underestimated. In the HH-model the stronger destabilizing contribution due to curvature-dependent erosion is to some extent compensated by the new stabilizing contribution to mass redistribution due to the angular dependence $D(\theta )$. This tendency is even more pronounced at higher ion energies. For 60 keV Ar ions on Si (experimentally studied by Datta et al. [52]) $D(\theta )$ has a nearly constant negative slope between 20° and 85°, which strongly reduces the curvature coefficient S _u,redist compared to the cf model calculation. According to the BH + CV model, for Ar and Xe irradiation of Si with energies of 10 keV and higher, mass redistribution would be the main reason for the surface instability along u-direction, whereas in the cf and HH models it is clearly the curvature-dependent erosion.

With SDTrimSP it is fairly easy to calculate crater functions also for high ion energies and complex targets. This is demonstrated in Fig. 12, where the crater functions for 40 keV Xe on Si incident at 60° are shown. For the calculation, I used 10⁶ sputtered and recoiled atoms, respectively, and 15 eV for the displacement energy. The redistribution crater has a size of several 10 nm. However, the average mass transport distance per recoil atom is only 0.07 nm so that the net mass transport of 963 recoil atoms per ion is δ_u,redist = 67.4 nm, which of course cannot be extracted from the plot. On the other hand, sputtered atoms appear at a mean distance of about δ_u,eros ≈ 10 nm away from the impact point. Because of Y·δ_u,eros > δ_u,redist, curvature-dependent erosion is the dominating effect at 60°.

Fig. 12

Crater functions for Si irradiated with 40 keV Xe ions incident at 60°

3.5 Simulations for Xe ions on a-C

In a recent paper, my group has published a study on ripple formation on a-C films under Xe ion irradiation [23]. In this study, the ion fluence was chosen just high enough to observe ripple patterns, to ensure the comparison with linear theories of ripple formation. The experimental results were compared with simulations based on curvature-dependent erosion according to the BH model (Eq. 9) and mass redistribution calculated with SDTrimSP, similar to Eq. 29. In these calculations a displacement energy of E _D = 28 eV was chosen, which annihilates most recoil events in particular at low energies. Because the BH model underestimates curvature-dependent erosion, the calculated S _u and S _v values in Ref. [23] favour mass redistribution as dominant effect. Here I present new simulation results shown in Fig. 13 for a displacement energy E _D = 0 eV at low ion energies ≤ 1 keV, E _D = 3 eV between 1 and 7 keV and E _D = 28 eV for 10 keV (The simulation for 10 keV and E _D = 3 eV gives the same result but requires about 10 times more computing time). It turns out that at low ion energies, the mass redistribution is indeed the most dominant process leading to parallel ripples for angles larger than about 50°–60°. Except for the 10-keV calculations, perpendicular ripples at large angles are unlikely, because the low sputter yield prevents the coefficient S _v to become negative. At 10 keV, parallel ripples between about 50° and 75° are due to both, curvature-dependent erosion and mass redistribution. At 200 eV the HH-model does not predict parallel ripples at 60°, in contrast to the experiment [23]. The reason is the calculated strong angular dependence D(θ). However, at 200 eV absolute values of D(θ) ≈ 0.5–1 nm corresponds to few atomic layers comparable to the surface roughness and the simulation may not adequately describe the experimental situation. Here the assumption D ≈ constant is favourable and the cf-model provides a good agreement with experiment.

Fig. 13

Curvature coefficients for Xe ion irradiation of a-C films with ion energies of 200 eV (left column), 1 keV (middle column) and 10 keV (right column), calculated according to the CV and BH model, the cf-model and the HH model. Solid circles total S _u coefficient, solid triangles total S _v coefficient, thick solid lines erosive contribution to S _u, dashed lines redistributive contribution to S _u

3.6 Estimate of the ripple wavelength

To estimate the ripple wavelength assuming ion-induced viscous flow as relevant relaxation mechanism we require values for the surface free energy γ and the irradiation induced viscosity η _S,RAD (see Eq. 3). The latter quantity is dependent on the ion flux and also the amount of displacements generated in the irradiated surface layer. We, therefore, expect a significant dependence on ion incidence angle and ion energy.

Mayr et al. [53, 54] investigated ion-induced viscous flow and introduced η _S,rad in units Pa·dpa, where dpa is the number of displacements per atom or the atomic fraction of Frenkel pairs, which was estimated using a typical displacement energy of 10 eV [53]. The scaling of η _S,rad with dpa allows an easy adjustment of η _S,rad to different irradiation conditions and was already applied by Madi et al. and Norris et al. [19, 22]. An ion fluence generating 1 dpa in the irradiated layer of atomic density n and thickness d comparable to the total width of the recoil depth distribution is given by

$$ \varPhi_{{ 1\;{\text{dpa}}}} = \frac{d \cdot n}{{N_{\text{D}} }}. $$

(34)

Here, N _D is the number of displacements generated per ion within the layer d. Because d and N _D depend on ion energy and incidence angle, $\eta_{\text{S,RAD}} \left( {\theta ,E_{\text{ion}} } \right)$ also varies with energy and incidence angle. The radiation-induced viscosity of an ion-irradiated surface layer of thickness d is then

$$ \eta_{\text{S,rad}} \left( {\theta ,E_{\text{ion}} } \right) = p_{0} \cdot \frac{{d\left( {\theta ,E_{\text{ion}} } \right) \cdot n}}{{N_{\text{D}} \left( {\theta ,E_{\text{ion}} } \right)}}, $$

(35)

given in units of Pa ions/cm². One should note, that scaling between different ion energies is problematic, because N _D strongly depends on the choice of the displacement energy E _D, the bulk binding energy E _B and even the cut-off energy E _cut-off. Typically this scaling procedure will overestimate $\eta_{\text{S,RAD}}$ and underestimate F _S,rad (Eq. 3) for low ion energies. On the other hand, for a given ion energy and fixed parameters to calculate N _D, Eq. 35 is suitable to determine the angular dependences η _S,rad (θ) and d(θ) with SDTrimSP. The coefficient for ion-induced viscous flow in Eq. 2 is then

$$ F_{\text{S,rad}} \left( {\theta ,E_{\text{ion}} } \right) \cdot d^{3} = \frac{\gamma \cdot J}{{3p_{0} n}} \cdot \cos \theta \cdot N_{\text{D}} \left( {\theta ,E_{\text{ion}} } \right) \cdot d^{2} \left( {\theta ,E_{\text{ion}} } \right). $$

(36)

This coefficient tends to zero for large angles of incidence, also because N _D and d are decreasing with increasing angle.

For silica, a few data for γ and η _S,rad can be found in the literature [30, 42, 59, 60] with values γ ≈ 0.3 J/m² and η _S,rad ≈ 5 × 10²²–1 × 10²⁵ Pa ions/cm². For high-energy ion irradiation of silica it was found that η _S,rad scales almost inversely to the maximum of the nuclear stopping S _nucl like $\, \eta_{\text{S,RAD}} \, = 1.79{ \times }10^{23} {\text{ Pa}}\;{\text{ions/cm}}^{2} \, \times \, S_{\text{nucl}}^{ - 0.83}$ with S _nucl given in units of keV/nm [42, 60]. Values of the surface free energy γ for C, Si and Ge can be found in Ref. [54, 61–63]. Here I use γ ≈ 1.4 J/m² for Si, γ ≈ 0.3 J/m² for a-SiO₂ and γ ≈ 1.9 J/m² for a-C. I will use the approximation $d \approx 2 \cdot D(\theta )$ for the irradiated layer thickness d, with D(θ) given by Eq. A.4. For Si and SiO₂, I adopt the values η _S,rad (Si) ≈ 9.6 × 10⁸ Pa dpa and η _S,rad (SiO₂) ≈ 3.6 × 10⁸ Pa dpa from [53, 54] to scale η _S,rad for different ion energies and angles of incidence. The ion flux is set to J = 1 × 10¹² ions/cm²/s, identical to the values used to calculate the curvature coefficients S _u and S _v.

For Si with E _D,Si = 15 eV and $\theta = 6 5^\circ$, I calculate $\eta_{\text{S,rad}} \approx 1.5 \times 10^{23}$ Pa ions/cm² (10 keV Xe), $\eta_{\text{S,rad}} \approx 1 \times 10^{23} \;{\text{Pa}}\;{\text{ions/cm}}^{2}$ (40 keV Xe), $\eta_{\text{rad}} \approx 3.6 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$ (1 keV Ar) and $\eta_{\text{rad}} \approx 9 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$ (250 eV Ar). The corresponding values used in the work of Norris et al. [22] would be 2 × 10²⁴ Pa ions/cm² for 250 eV Ar on Si. However, a displacement energy is not defined for amorphous targets and, moreover, for low-energy ions, a collision cascade is usually overwritten by a subsequent thermal spike [54, 58]. Therefore, $\eta_{{{\text{S}},{\text{rad}}}}$ is most probably smaller than the estimate via dpa. For Ar on Si with E = 1 keV, I use $\eta_{\text{S,rad}} \approx 1 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$ and for E = 250 eV $\eta_{\text{S,rad}} \approx 4 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$ to obtain ripple wavelengths in agreement with experimental data. For 500 eV Ar on SiO₂ and θ = 65° I use $\eta_{\text{rad}} \approx 2 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$, somewhat smaller than the estimated value $\eta_{\text{rad}} \approx 2.5 - 10 \times 10^{23} {\text{Pa}}\;{\text{ions/cm}}^{2}$, based on the data of [53, 54] and [40]. There are no literature data available on the radiation-induced viscosity of amorphous carbon. On the other hand, the experimental wavelength data of ripples on ta-C at 60° in the energy regime 200 eV to 10 keV [23] can be well reproduced with the simulations for $\eta_{\text{S,rad}} 60^\circ \approx 2 \times 10^{24} {\text{Pa}}\;{\text{ions/cm}}^{2}$.

The estimated ripple wavelength as function of ion incidence angle for 500 eV Ar on a-SiO₂, 1 keV Ar on Si and 10 keV and 40 keV Xe on Si is shown in Fig. 14. The calculated wavelengths for parallel ripples are in good agreement with experimental data [18, 47, 48, 64, 65]. For perpendicular ripples the agreement with the experimental data point is poor. The wavelengths of parallel ripples observed for 60 keV Ar ion irradiation of Si [52] are also reproduced by the calculations. The experimentally observed ripple wavelength of parallel ripples at 60° incidence angle for Xe ions onto a-C varies between about λ = 12 nm at 200 eV and λ = 40 nm at 10 keV [23]. These wavelengths can be reproduced by the simulation (Eq. 6) for a surface free energy for a carbon surface of γ = 1.9 J/m², η _rad ≈ 2 × 10²⁴ Pa ions/cm².

Fig. 14

Ripple wavelength as function of ion incidence angle calculated using Eq. 6 with parameters as discussed in Sect. 3.6 and curvature coefficients of the HH model for, a 500 eV Ar on a-SiO₂, b 1 keV Ar on Si, c 10 keV Xe on Si and d 40 keV Xe on Si. The experimental values are extracted from Ref. [47] for (a), Ref. [49] for (b), Ref. [64] for (c) and Refs. [18, 65] for (d). Solid and dashed lines represent wavelengths calculated for radiation-induced viscosity after Eq. 35 for parallel and perpendicular ripples, respectively

4 Discussion

The simulations I presented here are very similar to the crater function analyses discussed in several previous publications [22, 25–29]. However, up to now the crater function analysis relies on MD simulations of ion impact, which are feasible only for very low ion energies and a very limited number of projectiles. Monte Carlo simulations using SDTRimSP [36, 37] enable the calculation of curvature coefficients for almost any ion target combination and ion energies of several 10 keV and with extremely good statistics for typically more than 10⁵ ion impacts, more than 10⁵ sputtered atoms and several million recoil events. Furthermore, SDTrimSP and also TRIDYN [38] run in dynamic mode are able to include transient compositional changes of the target during ion irradiation. In this way it is possible to account for preferential sputtering in the case of compound materials such as SiO₂ and also the incorporation of ions into the materials as it is the case for Ga ion irradiation.

I introduce the variation of the thickness of the irradiated layer with ion incidence angle as an extension to the existing linear theories of pattern formation (BH model [1], CV model [18] and crater function models [22, 25–29]). This dependence D(θ) has a significant effect on the curvature coefficient not only for mass redistribution but also for the coefficient for ion-induced viscous flow. The decreasing thickness of the irradiated layer with increasing ion incidence angle gives rise to an additional term with positive sign to the curvature coefficient for mass redistribution S _u,redist. This term contributes to the stabilization of the surface in direction parallel to the projected ion beam direction, in particular at intermediate angles.

An additional contribution to the curvature coefficients arises from the relaxation of inward-directed mass transport. The corresponding term is proportional to a distance given by the erosion depth Y/n ^1/3 and has negative sign. Therefore, it reduces the redistributive curvature coefficients S _u,redist and S _v,redist. In the case of 250 eV Ar on Si the term eventually generates a negative coefficient S _v at angles above about 70° and thus explains correctly the occurrence of perpendicular ripple patterns.

The coefficients for curvature-dependent erosion calculated using SDTrimSP are significantly larger compared to the BH model calculations. This observation confirms the results of recent MD simulations studies [29], which indicated that a linear relation between an ellipsoidal Gaussian energy deposition and sputter yield is not fulfilled. My simulations show that the assumption of such a linear relation leads to a strong underestimation of curvature-dependent erosion by the BH model. To calculate erosive curvature coefficients with Monte Carlo or MD simulations one should first compare the angle-dependent sputter yields with experimental data. For the systems presented here such experimental data exist in the literature. In all cases the simulations (using tabulated surface binding energies) well reproduce the experimental sputter yields. The results presented here for Xe and Ar ions incident on Si targets and also Ar on a-SiO₂ show that curvature-dependent erosion makes a significant contribution to pattern formation and dominates at ion energies in the keV region. For the case 40 keV Xe on Si, as studied by Carter and Vishnyakov, mass redistribution is almost negligible for pattern formation at angles above about 40°. However, in all cases studied here, mass redistribution is responsible for a stable surface at near-normal ion incidence angles. Furthermore, for the case of very low ion energies, preferably heavy ions incident on a light matrix, sputtering is very weak and mass redistribution is the major process leading to the formation of parallel patterns. The model case here is Xe irradiation of a-C with E _ion ≤ 1 keV. The calculations presented here assume an amorphous target. However, many experiments were carried out with crystalline Si (001), which becomes amorphous after irradiation with a certain ion fluence. The role of crystal orientation on the pattern formation was investigated by several groups [65–67]. A recent study indicates that channelling effects may suppress a rapid amorphization, in particular for ion incidence angles of several degrees around 45° (<101> direction), and pattern formation may be retarded and should set in at somewhat higher ion fluences [67].

In a recent publication, our group speculated that mass redistribution would not contribute to stability or instability in v-direction (perpendicular ripples) [23]. This opinion was based on our calculations using CV-type mass redistribution and the BH-type curvature-dependent erosion. In hardly any case we obtained a surface instability in v-direction, because mass redistribution effects always lead to a stable surface. The statement made in [23] is not correct in general, but is valid for large angles of incidence. Due to the stronger contribution of curvature-dependent erosion and the relaxation term ~−Y/n ^1/3, the redistributive coefficient S _v,redist may indeed reach zero or negative values at larger angles of incidence. Now most of the calculations predict small negative S _v coefficients and thus perpendicular ripples at angles above about 60°–70°, in agreement with many experimental observations. At smaller angles, mass redistribution stabilizes the surface in v-direction as already shown by Davidovitch et al. [20] and crater function models [22, 26–28]. Therefore, the curvature coefficients calculated with SDTrimSP correctly predict the occurrence of perpendicular ripple patterns at larger ion incidence angles. There is an angular regime where the simulations predict a surface, which is instable in both parallel and perpendicular direction. This is also compatible with experimental observations of rather complex, probably superimposed parallel and perpendicular ripple patterns [19, 23, 46, 49–51, 72]. Only perpendicular ripples should appear for ion incidence angles above about 70°–80° and the occurrence of perpendicular ripples is a measure of the contribution of curvature-dependent sputtering to pattern formation. The systems where perpendicular ripples are observed experimentally may, therefore, act as test cases for pattern formation models (e.g. 250–2,000 eV Ar on Si [46, 48, 49, 68, 69], 5 keV Xe on Fe and Ni [70, 71], 5–10 keV Xe on Si [64, 72], 800 eV Ar on Au and Ag [73, 74] keV Ar ions on different metals [75], 500 eV Ar on SiO₂ [47]). My simulations are in good agreement with many of these experimental observations.

The calculation of curvature coefficients using SDTrimSP or MD simulations requires an adequate definition of the surface. At the “interaction surface” the interaction between ions and target atoms sets in and its position depends on the maximum impact parameters for binary collisions. The “geometrical surface”, set at x = 0, only distinguishes between vacuum and solid. The centre positions of target atoms are at x < 0. Depending on the maximum possible impact parameter, the “interaction surface” is typically about x _C = 0.5 nm above the “geometrical surface”. An ion incident at grazing angles θ can, therefore, interact over a distance x _C·tanθ with target atoms before entering the target at x = 0. For larger ion energies generating a sizeable collision cascade this difference is irrelevant. However, for ion energies below about 1 keV the size of the collision cascade, i.e. ion and recoil ranges, are small and the correct ion impact point should be chosen at the “interaction surface”. SDTrimSP uses by default the ion impact point (−x _C, 0, 0). In some publications crater functions are shown for different ion incidence angles [27–29]. From these plots it seems that the ion impact point is set into the “geometrical surface”. Choosing this impact point into the geometrical surface will strongly reduce the 1st moment of the erosive crater function. In particular, at low ion energies this may lead to the conclusion that erosive effects are irrelevant. The calculations in the case of a strongly reduced 1st moment of the erosive crater function do not predict a ripple orientation and instead parallel ripples up to about 85°, which is not in agreement with experimental observations [19, 47]. The comparison of my calculations based on SDTrimSP and the calculations based on MD simulation [22] for 250 eV Ar on Si also reveal significantly lower 1st moments of the erosive crater function obtained from MD. It should be clarified if this may be related to the choice of the impact point.

To estimate the most stable ripple wavelength λ(θ) it is necessary to take into account not only the proper angular dependence of the curvature coefficients S _u and S _v, but also the angular and ion energy dependence of the parameter F _S,rad(θ, E _ion)·d(θ)³, describing ion-induced viscous flow in a layer of thickness d(θ), varying with ion incidence angle. Calculated wavelengths for parallel ripples, based on a limited number of available data for the surface free energies and ion-induced viscosities, are in reasonable agreement with experimental data. Although my simulations correctly predict the angular regime where perpendicular ripples should occur, the estimates of the wavelength of perpendicular ripples are in poor agreement with experimental data and require further investigation.

The case of ripple pattern formation on metallic substrates is a special case. First of all, most metals typically do not amorphize and a proper displacement energy has to be chosen for the simulation of curvature coefficients. A large displacement energy almost completely resets recoil atoms to their initial positions and thus completely erases mass redistribution, in particular in the case of low ion energies. This is the reason why only perpendicular ripples were experimentally observed for a broad range of ion incidence angles for 200 eV Ne on Pt [23] and 650 eV Ar on Au [74]. Second, metal substrates are either single crystalline or polycrystalline and ion channelling effects may play an important or even dominating role for pattern formation. The present simulations using SDTrimSP assume amorphous targets and are, therefore, not really suited to describe pattern formation on metallic targets. Third, the assumption of negligible surface diffusion (B ≈ 0) may not be valid for metallic targets.

One assumption made in most continuum models (CV model, BH model, crater function models and non-linear extensions) of pattern formation is the incompressibility of the irradiated films (Eq. 13). It is assumed that density variations due to mass redistribution are instantaneously relaxed and lead to local height changes of the irradiated surface layer. Other models explain the pattern formation as due to ion-induced compressive stress [11, 16]. However, these models also assume incompressibility (Eq. 3 of Ref. [11]) or do not make explicit assumptions about the layer density [16]. One rather introduces a stress field generated by point defects and a surface curvature. If point defects would give rise to a (steady-state) density variation ρ(x, y, z) or ρ(u, w, v) within the irradiated film one should modify the corresponding boundary condition (Eq. 13) to solve the Navier–Stokes equation. Qualitatively, an incomplete density relaxation would strongly reduce the CV effect of mass redistribution because height variations due to redistribution of surface near recoil atoms are suppressed. Instead, one could introduce curvature coefficients due to compressive stress according to Eq. 1 and 2 of Ref. [16]. SDTrimSP simulations, carried out in static or dynamic mode, provide all data of the individual collision cascades. From these data it is possible to extract, e.g. the velocity field of the lateral atomic drift of recoil atoms as function of depth. It is also possible to determine variations of the atomic density as function of depth in case of stoichiometry changes in compound systems. However, it is not possible to predict vacancy-related density changes and defect-induced stress fields in the irradiated layer using SDTrimSP or related programs. Therefore, stress-induced effects are beyond the possibilities of the Monte Carlo binary collision approximation programs. Furthermore, deviations from the non-compressibility condition would require a continuum theory with appropriate density field ρ(x, y, z) different from the assumption of constant density in Eq. 13.

SDTrimSP simulations carried out in dynamic mode will take care of stoichiometry changes within the irradiated layer due to preferential sputtering and ion or atom incorporation. Local density variations are also taken into account in dynamic mode simulations based on an interpolation between, e.g. the density of the elemental species and the density of a given compound. For the case of a SiO₂ target, the main effect is preferential sputtering which leads to an SiO stoichiometry at the surface. For Ga ion irradiation of Si or SiO₂, the incorporation and sputtering of non-volatile Ga can be taken into account in dynamic mode, leading to a Ga concentration of about 10 at.% within the irradiated layer. In the simulations using noble gas ion irradiation of substrates, I have neglected the incorporation of noble gas atoms and simulations were carried out in static mode. This decision is motivated by measurements using Rutherford backscattering, showing that the Xe concentration in Si in steady state is at most 3 at.%. This does not significantly affect the sputter yield and the collision cascade parameters describing mass redistribution. However, the incorporation of noble gas atoms may have a significant influence on pattern formation. If gas atoms occupy vacancies (or under-coordinated low density regions in an amorphous layer) a density relaxation may be suppressed. Furthermore, the incorporation of gas atoms in the form of small bubbles may produce compressive stress and influence the viscoelastic properties of the irradiated layer. In principle, SDTrimSP would allow to calculate density variations in the irradiated layer due to incorporation of (solid) noble gas atoms, but without including the effect of vacancies. The role of noble gas incorporation is beyond the scope of this study, but is worthwhile to be considered in future experimental and theoretical work.

5 Conclusions

In this work, I discussed the issue of surface instability due to sputter erosion and ion-induced mass redistribution. I calculated the respective curvature coefficients used in the linear BH and CV continuum theories from Monte Carlo simulations of the 3-dimensional collision cascade with SDTrimSP. SDTrimSP simulations provide an easy and fast method to predict ion-induced ripple pattern formation even for large ion energies and complex targets and are, therefore, a valuable alternative to calculations based on MD simulations

The linear BH [1] and CV [18, 20] continuum theories which are also used in crater function models [22, 25–29] are extended regarding the angle-dependent thickness variation $D(\theta )$ of the ion-irradiated surface layer and also a term related to the relaxation of inward-directed mass transport. The thickness variation with ion incidence angle leads to a significant stabilizing contribution at intermediate angles for the u-direction, i.e. the projected direction of the incident ion beam. The inward mass relaxation contributes to both curvature coefficients S _u and S _v with a negative term ~Y/n ^1/3. At large ion incidence angles, the coefficient S _v,redist may then reach values close to zero, so that curvature-dependent erosion can lead to perpendicular ripple patterns.

The BH model with the assumption of a linear relation between ellipsoidal energy distribution and local sputter yield underestimates the effect of curvature-dependent erosion on the pattern formation. The SDTrimSP simulations reveal a much stronger and essential contribution of curvature-dependent erosion to pattern formation in most cases. According to my simulations, only for irradiation of light targets at very low energies (e.g. ≤1 keV Xe ions on a-C) the erosive contribution is small because of a small sputter yield and pattern formation is mainly caused by ion-induced mass redistribution. In all other cases, in particular for ion energies in the keV regime or higher, curvature-dependent erosion is a significant and often the dominating contribution to ripple pattern formation. Even for 500 eV Ar ions on SiO₂ the simulations predict that curvature-dependent erosion is responsible for an orientation transition at about 70°, which is in good agreement with the experiment [47]

The calculated ripple wavelengths are in reasonable agreement with experimental data and support ion-induced viscous flow as a major smoothing mechanism for the case of parallel ripples. Further investigations are required for a satisfactory description of the wavelength of perpendicular ripple patterns.

Appendix: computational details

The calculations of the three-dimensional collision cascades were done with the Monte Carlo Code SDTrimSP V5.05 [36, 37]. SDTrimSP is to a large extent identical to TRIDYN [38] but provides much more input and output options. Important input parameters for the simulations are the surface binding energy E _S, the bulk binding energy E _B and the displacement energy E _D. Another energy parameter is the cut-off energy E _cut-off ≈ 0.2–1 eV above which an atom’s path is followed. E _S derived from vaporization enthalpies and is tabulated in SDTrimSP. The bulk binding energy only applies to crystalline targets and is related to the formation energy of vacancies. For our simulations we use E _B = 0 eV. The displacement energy determines the recombination of low-energy recoils with its own vacancy. The proper experimental displacement energy E _D should be used to simulate crystalline targets; otherwise we can set E _D = 0–2 eV. Displacement energies can be taken from published tabulated experimental data [55–57]. In general, the choice of small or zero values of E _B and E _D is not critical for amorphous targets. For ion energies below 1 keV it is recommended to choose E _B = 0 eV and E _D ≤ 2 eV because otherwise the collision cascade is reduced to only a few but highly energetic recoil events. At low ion energies, a thermal spike is generated and the collision cascade region can be considered as a “molten” region for a short period of time (picoseconds), which may justify the choice of E _B = E _D = 0 eV [58]. A value E _D > 0 is favourable for higher ion energies of several keV or tens of keV and will significantly reduce the computing time, without influencing the simulation results. I have carried out a variety of simulations with different values for E _B and E _D which confirm the above recommendations for the proper choice of these two parameters.

Simulations for several exemplary cases for Si, a-SiO₂ (silica) and a-C substrates are presented. The simulations for ion incidence angular steps of 10° up to an angle of 60° and steps of 5° for larger angles typically take into account N _ion = 10⁵ incident ions and the first 10⁵ recoil events per simulation (“iout_part = 100000”) are stored as output file “partic_stop_r.dat”. Mean values of the recoil distributions and the sputter distributions were also derived from all recoil events (up to several million events) and all sputtered atoms. The number N _ko(θ) of knock-on collision events and N _D(θ) of displacements per ion with E > E _D can be found in file “output.dat”. Here N _D is the number of permanently displaced recoils per ion. A permanently displaced recoil atom is obtained for an energy transfer in a nuclear collision larger than the displacement energy E _D. Recoil atoms with energy E _recoil < E _D are reset to their original position unless they are sputtered off the surface. Other data available from SDTrimSP are, e.g. number, energy and angular emission distribution of reflected ions. For static mode simulations, the sputter yield Y(θ) is listed in the file “output.dat”. The fluence- (or time)-dependent sputter yields are listed in “backsputt.f31” in case of dynamic simulations. Dynamic simulations take into account transient stoichiometry changes due to implantation of ions and preferential sputtering and are carried out, e.g. for a-SiO₂ targets. All other details of the back-sputtered recoil atoms are stored in the file “partic_back_r”. The derivative of the sputter yield ${\text{d}}Y/{\text{d}}\theta$is calculated using an analytical fit function (Eq. 7 of Ref. [23]) to the discrete sputter yield data obtained from SDTrimSP. If possible, calculated sputter yields were compared to published, experimental sputter yield data and a good quantitative agreement, also for the angle dependence of the sputter yield, was found.

SDTrimSP and TRIDYN use a coordinate system (x, y, z) with the x-axis pointing opposite to the surface normal and the y-axis lying in the surface typically along the projected beam direction. The coordinate system (u, v, w) commonly used to describe pattern formation, e.g. in the BH model [1], has the w-axis parallel to the global surface normal. Here I use the system (u, v, w) = (y, −z, −x) and a system (u′, v′, w′) for the local surface (see Fig. 1), so we can retain the (x, y, z)-denotation used in the SDTrimSP output files.

The lateral distribution of the initial locations of sputtered atoms is listed in file “partic_back_r” and the average position $\delta_{\text{u,eros}} (\theta )$ is obtained from y _start data in analogy to the calculation of the 1st moment $M_{(\theta )}^{(1)}$ of a crater function [26]. For simulations carried out with typically N _ion = 10⁵ incident ions and a number of Z _SP = Y·N _ion sputtered atoms (typically several hundred thousand) I calculate

$$ \delta_{\text{u,eros}} (\theta ) = \frac{1}{{Z_{\text{sp}} }}\sum\limits_{i = 1}^{Z_{\text{sp}}} {y_{\text{i,start}} (\theta )} , $$

(A.1)

and the first moment of the erosion crater function (similar to Eq. (47) of Ref. [26]).

$$ M_{\text{eros}}^{(1)} (\theta ) = - \frac{Y(\theta )}{n} \cdot \frac{1}{{Z_{\text{sp}} }}\sum\limits_{i = 1}^{{Z_{\text{sp}} }} {y_{\text{i,start}} (\theta )} = - \frac{Y(\theta )}{n} \cdot \delta_{\text{u,eros}} (\theta ). $$

(A.2)

The BH theory uses

$$ \delta_{\text{u,BH}} (\theta ) = - a \cdot \varGamma_{1} (\theta )\quad {\text{and}}\quad \delta_{\text{v,BH}} (\theta ) = - a \cdot \varGamma_{2} (\theta ), $$

(A.3)

where a is the depth of the maximum of the recoil distribution at 0° ion incidence and Γ₁ and Γ₂ are the curvature coefficients described in Ref. [1]. In order to compare with the BH theory, I also calculated the parameters Γ₁ and Γ₂ with SDTrimSP. The relevant parameters a, σ and μ to define the energy ellipsoid are calculated as described in Ref. [23]. The parameters a and σ are obtained from a Gaussian fit to the recoil depth distribution (x _end values in “partic_stop_r”) for 0° ion incidence. Parameter μ is obtained from a Gaussian fit to either the y or z lateral recoil distributions (y _end or z _end values in “partic_stop_r”).

In SDTrimSP, the initial target atom centre positions only exist for x ≥ 0. The “geometrical surface” is, therefore, a plane at x = 0. However, the interaction of projectiles with the target atoms starts at a position (−x _C, 0, 0), with x _C ≈ 0.3–0.5 nm related to the maximum possible impact parameter (see Eq. 7.1.15 and Fig. 7.3 in Ref. [37]). Therefore, the actual surface (“interaction surface”) in SDTrimSP is a plane at x = −x _C and the actual ion impact point has the coordinates (−x _C, 0, 0). Recoils reaching the surface but are not sputtered may come to rest in between the x = −x _C and x = 0 planes. The correct choice of the ion impact point (−x _C, 0, 0) is important in particular for grazing ion incidence where ions will already interact with target atoms along a lateral distance $x_{\text{C}} \cdot \tan \theta$ before they cross the plane at x = 0. SDTrimSP uses by default the ion impact point (−x _C, 0, 0). Therefore, in the SDTrimSP output files all y-coordinates of recoils and sputtered atoms seem to be shifted towards positive y-values by $x_{\text{C}} \cdot \tan \theta$. This shift is significant at low ion energies, when the size of the collision cascade volume is small compared to $x_{\text{C}} \cdot \tan \theta$. In such cases the erosion parameter $\delta_{\text{u,eros}} (\theta )$ and the 1st moment of the erosion crater function $M_{\text{eros}}^{(1)} (\theta )$) are influenced by x _C at large θ values. There is no influence of x _c on the mass redistribution, because only the differences between recoil start and end positions are considered.

The mean depth of the recoil distribution D(θ) is obtained from the x _end positions of Z _R = N _ion·N _D calculated recoils events, where x _end is the x-coordinate (normal to the surface) of the origin of recoils.

$$ D(\theta ) = \frac{1}{{Z_{\text{R}} }}\sum\limits_{i = 1}^{{Z_{\text{R}} }} {x_{\text{i,end}} (\theta )} . $$

(A.4)

Values for mass transport parallel to the surface of Z _R target atoms recoiled with energy larger than E _D and stopped inside the target are listed as y _start and y _end positions in the file “partic_stop_r.dat” or are directly obtained as mean value of all recoil events. For a number of Z _R recoils (typically several million) the parallel mass transport distance per ion $\delta_{\text{u}} (\theta )$ is given by

$$ \delta_{\text{u}} (\theta ) = N_{\text{ko}} (\theta ) \cdot \frac{1}{{Z_{\text{R}} }}\sum\limits_{i = 1}^{{Z_{\text{R}} }} {\left( {y_{\text{i,end}} (\theta ) - y_{\text{i,start}} (\theta )} \right)} . $$

(A.5)

and the redistribute crater function is (similar to Eq. (49) of Ref. [26])

$$ M_{\text{redist}}^{(1)} (\theta ) = \frac{{N_{\text{ko}} (\theta )}}{n} \cdot \frac{1}{{Z_{\text{R}} }}\sum\limits_{i = 1}^{{Z_{\text{R}} }} {\left( {y_{\text{i,end}} (\theta ) - y_{\text{i,start}} (\theta )} \right)} . $$

(A.6)

The CV model [18] uses

$$ \delta_{\text{u,CV}} (\theta ) = N_{\text{ko}} (\theta ) \cdot \delta_{0} \cdot \sin \theta $$

(A.7)

or the corresponding first moment of the crater function

$$ M_{\text{redist,CV}}^{(1)} (\theta ) = \frac{{N_{\text{ko}} (\theta )}}{n} \cdot \delta_{0} \cdot \sin \theta , $$

(A.8)

where δ₀ is the inward-directed mass transport distance per ion at 0° incidence, given by

$$ \delta_{0} = N_{\text{ko}} (0) \cdot \frac{1}{{Z_{\text{R}} }}\sum\limits_{i = 1}^{{Z_{\text{R}} }} {\left( {x_{\text{i,end}} (0) - x_{\text{i,start}} (0)} \right)} . $$

(A.9)

The inward-directed mass transport distance per ion for arbitrary incidence angles θ is

$$ - \delta_{\text{w}} (\theta ) = N_{\text{ko}} (\theta ) \cdot \frac{1}{{Z_{\text{R}} }}\sum\limits_{i = 1}^{{Z_{\text{R}} }} {\left( {x_{\text{i,end}} (\theta ) - x_{\text{i,start}} (\theta )} \right)} . $$

(A.10)

In the case that E _D > 0 is specified, the number of displacements per ion N _D is used instead of N _ko. The simple assumption made in the CV model that $\delta_{\text{u}} (\theta ) \cong \delta_{0} \sin \theta$ with $\delta_{0} = \delta_{\text{u}} (\theta = 0)$ is not valid for larger angles of incidence. This is shown in Fig. 15 for a SDTrimSP simulation for 10 keV Xe ions incident on Si. The decreasing value $\delta_{\text{u}} (\theta )$ at larger angles is mainly due not only to the decreasing number of displaced atoms but also to a more inward-directed mass transport caused by inelastic reflected ions. Crater function calculations also return a similar angular dependence of $\delta_{\text{u}} (\theta )$ [22, 28].

Fig. 15

Angular dependence of the number N _D of permanently displaced atoms and the lateral mass transport distance δ_u(θ) calculated with SDTrimSP for 10 keV Xe ions in Si and displacement energy E _D = 15 eV. The solid line is a fit to the discrete SDTrimSP data using the formula shown in the figure