Pattern Transformation in Higher-Order Lumps of the Kadomtsev–Petviashvili I Equation

Abstract

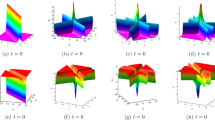
Pattern formation in higher-order lumps of the Kadomtsev–Petviashvili I equation at large time is analytically studied. For a broad class of these higher-order lumps, we show that two types of solution patterns appear at large time. The first type of patterns comprises fundamental lumps arranged in triangular shapes, which are described analytically by root structures of the Yablonskii–Vorob’ev polynomials. As time evolves from large negative to large positive, this triangular pattern reverses itself along the x-direction. The second type of patterns comprise fundamental lumps arranged in non-triangular shapes in the outer region, which are described analytically by nonzero-root structures of the Wronskian–Hermit polynomials, together with possible fundamental lumps arranged in triangular shapes in the inner region, which are described analytically by root structures of the Yablonskii–Vorob’ev polynomials. When time evolves from large negative to large positive, the non-triangular pattern in the outer region switches its x and y directions, while the triangular pattern in the inner region, if it arises, reverses its direction along the x-axis. Our predicted patterns at large time are compared to true solutions, and excellent agreement is observed.

Appendix

In this appendix, we briefly derive the bilinear higher-order lump solutions presented in Theorem 1.

Under the variable transformation $u=2(\log \tau )_{xx}$ and notations of $x_1=x, x_2=\text {i} y$ and $x_3=-4t$, the KP-I equation (3) is converted to the bilinear equation

$$\begin{aligned} (D_{x_1}^4-4D_{x_1}D_{x_3}+3D_{x_2}^2) \, \tau \cdot \tau =0, \end{aligned}$$

(125)

where D is Hirota’s bilinear differential operator. It is well-known that if $m_{ij}$, $\phi _i$ and $\psi _j$ are functions of $(x_1, x_2, x_3)$ and satisfy the following differential equations

$$\begin{aligned}&\partial _{x_1}m_{ij}=\phi _i \psi _j, \end{aligned}$$

(126)

$$\begin{aligned}&\partial _{x_n}\phi _i = \partial _{x_1}^n \phi _i, n=2, 3, \end{aligned}$$

(127)

$$\begin{aligned}&\partial _{x_n}\psi _j = (-1)^{n-1}\partial _{x_1}^n \psi _j, \quad n=2, 3, \end{aligned}$$

(128)

then the $\tau$ function

$$\begin{aligned} \tau =\det _{1\le i,j\le N}\left( m_{ij}\right) \end{aligned}$$

(129)

would satisfy the above bilinear equation (Hirota 2004). To derive higher-order lump solutions, we define $m_{ij}$, $\phi _i$ and $\psi _j$ as

$$\begin{aligned} m_{ij}=\mathcal {A}_i \mathcal {B}_{j} \frac{1}{p+q} e^{\xi _i+\eta _j}, \quad \phi _i=\mathcal {A}_i e^{\xi _i}, \quad \psi _j=\mathcal {B}_{j} e^{\eta _j}, \end{aligned}$$

(130)

where

$$\begin{aligned} \mathcal {A}_{i}&= \frac{1}{ n_i !}(p\partial _{p})^{n_i}, \quad \mathcal {B}_{j}=\frac{1}{ n_j !}(q\partial _{q})^{n_j}, \end{aligned}$$

(131)

$$\begin{aligned} \xi _i&= px_1+p^2x_2+p^3x_3+\xi _{i,0}(p), \quad \eta _j=qx_1-q^2x_2+q^3x_3+\eta _{j,0}(q), \end{aligned}$$

(132)

$(n_1, n_2, \ldots , n_N)$ is a vector of arbitrary positive integers, p, q are arbitrary complex constants, and $\xi _{i,0}(p)$, $\eta _{j,0}(q)$ are arbitrary complex functions of p and q. It is easy to see that these $m_{ij}$, $\phi _i$ and $\psi _j$ functions satisfy the differential Eqs. (126)–(128). Thus, the above $\tau$ function would satisfy the bilinear Eq. (125). To guarantee that this $\tau$ function is real-valued, we impose the parameter constraints

$$\begin{aligned} q=p^*, \quad \eta _{j,0}(q)=[\xi _{j,0}(p)]^*. \end{aligned}$$

(133)

Under these constraints, $\eta _j=\xi _j^*$, $m_{n_i, n_j}^*=m_{n_j, n_i}$, and thus $\tau$ in (129) is real. In addition, it is easy to see that $\tau$ is the determinant of a Hermitian matrix $M=\mathrm{mat}_{1\le i,j\le N}(m_{ij})$. Furthermore, M is positive definite, since for any nonzero column vector $\mathbf{v} =(v_1,v_2,\ldots ,v_N)^T$, with the superscript “T” representing vector transpose,

$$\begin{aligned} \mathbf{v} ^{*T} M \mathbf {v}=&\sum _{i,j=1}^{N} v_{i}^*v_{j} \mathcal {A}_{i} \mathcal {B}_{j} \frac{e^{\xi _i+\eta _j}}{p+q} = \int _{-\infty }^{x_1} \sum _{i,j=1}^{N} v_{i}^*v_{j} \mathcal {A}_{i} \mathcal {B}_{j} e^{\xi _i+\eta _j}dx_1 \nonumber \\ =&\int _{-\infty }^{x_1} \left| \sum _{i=1}^{N} v_{i}^*\mathcal {A}_{i} e^{\xi _i}\right| ^2 dx_1>0. \end{aligned}$$

(134)

Here, we have assumed $\Re (p)>0$ without loss of generality. Thus, $\tau$ is always positive.

Next, we need to simplify the matrix elements of this $\tau$ determinant and derive their more explicit algebraic expressions. This simplification is very similar to that we performed in Ohta and Yang (2012), Yang and Yang (2021c). By expanding $\xi _{i,0}(p)$ into a certain series containing complex parameters ${{\varvec{a}}}_{i}=\left( a_{i,1}, a_{i,2}, \ldots \right)$ and repeating the calculations of Ohta and Yang (2012), Yang and Yang (2021c), we can show that the matrix element $m_{ij}$ in (130) can be reduced to the expression given in Eq. (9) of Theorem 1. Since $\tau$ is positive, we can readily see that the reduced $\sigma$ determinant in Theorem 1 is positive as well. Thus, the resulting solution $u=2(\log \sigma )_{xx}$ is real-valued and nonsingular.

Regarding polynomial degrees of the determinant $\sigma (x,y,t)$, by rewriting this determinant as a larger one in Eq. (68) and performing Laplace expansion, we can readily see that its degrees in (x, y, t) are all $2\rho$, with $\rho$ given in Eq. (13).

We would like to make a comment here regarding the choice of differential operators in Eq. (131). Obviously, we can also choose more general forms of these differential operators, such as

$$\begin{aligned} \mathcal {A}_{i}=\frac{1}{ n_i !}\left( f(p)\partial _{p}\right) ^{n_i}, \quad \mathcal {B}_{j}=\frac{1}{ n_j !}\left( f(q)\partial _{q}\right) ^{n_j}, \end{aligned}$$

(135)

where f(p) is an arbitrary function, and the resulting $\tau$ function (129) would still satisfy the bilinear equation (125). However, such additional freedoms in the differential operators will not produce new higher-order lump solutions. To see why, we can rewrite this $\mathcal {A}_{i}$ as

$$\begin{aligned} \mathcal {A}_{i}=\frac{1}{ n_i !}\left( \frac{f(p)}{p} p\partial _{p}\right) ^{n_i}=\sum _{k=0}^{n_i} c_{i,k}\frac{1}{(n_i-k)!} (p\partial _p)^{n_i-k}, \end{aligned}$$

(136)

where $c_{i,k}$ are p-dependent complex constants. Similar treatments can be made on $\mathcal {B}_{j}$. These differential operators in summation form are similar to those taken in Ohta and Yang (2012). We can directly show that the $m_{ij}$ matrix element with these differential operators of summation form can be converted to one with these differential operators as a single term in (131), after parameters ${{\varvec{a}}}_{i}$ in the series expansion of $\xi _{j,0}(p)$ are redefined properly. Thus, no new solutions are produced.