Skip to main content
SpringerLink
Log in

A Mathematical Framework for Critical Transitions: Normal Forms, Variance and Applications

  • Published:
Journal of Nonlinear Science Aims and scope Submit manuscript

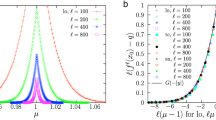
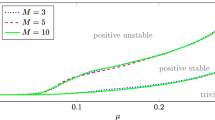
Abstract

Critical transitions occur in a wide variety of applications including mathematical biology, climate change, human physiology and economics. Therefore it is highly desirable to find early-warning signs. We show that it is possible to classify critical transitions by using bifurcation theory and normal forms in the singular limit. Based on this elementary classification, we analyze stochastic fluctuations and calculate scaling laws of the variance of stochastic sample paths near critical transitions for fast-subsystem bifurcations up to codimension two. The theory is applied to several models: the Stommel–Cessi box model for the thermohaline circulation from geoscience, an epidemic-spreading model on an adaptive network, an activator–inhibitor switch from systems biology, a predator–prey system from ecology and to the Euler buckling problem from classical mechanics. For the Stommel–Cessi model we compare different detrending techniques to calculate early-warning signs. In the epidemics model we show that link densities could be better variables for prediction than population densities. The activator–inhibitor switch demonstrates effects in three time-scale systems and points out that excitable cells and molecular units have information for subthreshold prediction. In the predator–prey model explosive population growth near a codimension-two bifurcation is investigated and we show that early-warnings from normal forms can be misleading in this context. In the biomechanical model we demonstrate that early-warning signs for buckling depend crucially on the control strategy near the instability which illustrates the effect of multiplicative noise.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  • Alley, R.B., Marotzke, J., Nordhaus, W.D., Overpeck, J.T., Peteet, D.M., Pielke, R.A. Jr., Pierrehumbert, R.T., Rhines, P.B., Stocker, T.F., Talley, L.D., Wallace, J.M.: Abrupt climate change. Science 299, 2005–2010 (2003)

    Article  Google Scholar 

  • Andronov, A.A., Leontovich, E.A., Gordon, I.I., Maier, A.G.: Qualitative Theory of Second-Order Dynamical Systems. Wiley, New York (1973)

    Google Scholar 

  • Arnold, L.: Random dynamical systems. In: Dynamical Systems (Montecatini Terme, 1994), pp. 1–43. Springer, Berlin (1995)

    Chapter  Google Scholar 

  • Arnold, L.: Random Dynamical Systems. Springer, Berlin (2003)

    Google Scholar 

  • Arnold, V.I.: Encyclopedia of Mathematical Sciences: Dynamical Systems V. Springer, Berlin (1994)

    Google Scholar 

  • Ashwin, P., Wieczorek, S., Vitolo, R., Cox, P.: Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Philos. Trans. R. Soc. A 370, 1166–1184 (2012)

    Article  Google Scholar 

  • Barkley, D.: A model for fast computer simulation of waves in excitable media. Physica D 49, 61–70 (1991)

    Article  Google Scholar 

  • Bazykin, A.D.: In: Khibnik, A.I., Krauskopf, B. (eds.) Nonlinear Dynamics of Interacting Populations. World Scientific, Singapore (1998)

    Google Scholar 

  • Bender, C.M., Orszag, S.A.: Asymptotic Methods and Perturbation Theory. Springer, Berlin (1999)

    MATH  Google Scholar 

  • Berglund, N., Gentz, B.: The effect of additive noise on dynamical hysteresis. Nonlinearity 15, 605–632 (2002a)

    Article  MathSciNet  MATH  Google Scholar 

  • Berglund, N., Gentz, B.: Metastability in simple climate models: pathwise analysis of slowly driven Langevin equations. Stoch. Dyn. 2, 327–356 (2002b)

    Article  MathSciNet  MATH  Google Scholar 

  • Berglund, N., Gentz, B.: Pathwise description of dynamic pitchfork bifurcations with additive noise. Probab. Theory Relat. Fields 3, 341–388 (2002c)

    Article  MathSciNet  Google Scholar 

  • Berglund, N., Gentz, B.: Geometric singular perturbation theory for stochastic differential equations. J. Differ. Equ. 191, 1–54 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  • Berglund, N., Gentz, B.: On the noise-induced passage through an unstable periodic orbit I: two-level model. J. Stat. Phys. 114(5), 1577–1618 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Berglund, N., Gentz, B.: Noise-Induced Phenomena in Slow-Fast Dynamical Systems. Springer, Berlin (2006)

    MATH  Google Scholar 

  • Berglund, N., Gentz, B.: On the noise-induced passage through an unstable periodic orbit II: the general case (2012). arXiv:1208.2557

  • Berglund, N., Landon, D.: Mixed-mode oscillations and interspike interval statistics in the stochastic FitzHugh–Nagumo model. Nonlinearity 25, 2303–2335 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Berglund, N., Gentz, B., Kuehn, C.: Hunting French ducks in a noisy environment. J. Differ. Equ. 252(9), 4786–4841 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Boettinger, C., Hastings, A.: Quantifying limits to detection of early warning for critical transitions. J. R. Soc. Interface 9(75), 2527–2539 (2012)

    Article  Google Scholar 

  • Brackley, C.A., Ebenhöh, O., Grebogi, C., Kurths, J., de Moura, A., Romano, M.C., Thiel, M.: Introduction to focus issue: dynamics in systems biology. Chaos 20, 045101 (2010)

    Article  Google Scholar 

  • Broer, H.W., Kaper, T.J., Krupa, M.: Geometric desingularization of a cusp singularity in slow-fast systems with applications to Zeeman’s examples. J. Differ. Equ., 1–46 (2012, submitted). Preprint

  • Carpenter, S.R., Brock, W.A.: Rising variance: a leading indicator of ecological transition. Ecol. Lett. 9, 311–318 (2006)

    Article  Google Scholar 

  • Carpenter, S.R., Brock, W.A., Cole, J.J., Kitchell, J.F., Place, M.L.: Leading indicators of trophic cascades. Ecol. Lett. 11, 128–138 (2008)

    Google Scholar 

  • Cessi, P.: A simple box model of stochastically forced thermohaline circulation. J. Phys. Oceanogr. 24, 1911–1920 (1994)

    Article  Google Scholar 

  • Chiba, H.: Periodic orbits and chaos in fast-slow systems with Bogdanov–Takens type fold points. J. Differ. Equ. 250, 112–160 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Clark, J.S., Carpenter, S.R., Barber, M., Collins, S., Dobson, A., Foley, J.A., Lodge, D.M., Pascual, M., Pielke, R. Jr., Pizer, W., Pringle, C., Reid, W.V., Rose, K.A., Sala, O., Schlesinger, W.H., Wall, D.H., Wear, D.: Ecological forecasts: an emerging imperative. Science 293, 657–660 (2001)

    Article  Google Scholar 

  • Dakos, V., Scheffer, M., van Nes, E.H., Brovkin, V., Petoukhov, V., Held, H.: Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. USA 105(38), 14308–14312 (2008)

    Article  Google Scholar 

  • Dakos, V., van Nes, E.H., Donangelo, R., Fort, H., Scheffer, M.: Spatial correlation as leading indicator of catastrophic shifts. Theor. Ecol. 3(3), 163–174 (2009)

    Article  Google Scholar 

  • Dakos, V., Kéfi, M., Rietkerk, M., van Nes, E.H., Scheffer, M.: Slowing down in spatially patterned systems at the brink of collapse. Am. Nat. 177(6), 153–166 (2011)

    Article  Google Scholar 

  • Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Cambridge University Press, Cambridge (1992)

    Book  MATH  Google Scholar 

  • Desroches, M., Guckenheimer, J., Kuehn, C., Krauskopf, B., Osinga, H., Wechselberger, M.: Mixed-mode oscillations with multiple time scales. SIAM Rev. 54(2), 211–288 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  • Ditlevsen, P.D., Johnsen, S.J.: Tipping points: early warning and wishful thinking. Geophys. Res. Lett. 37, 19703 (2010)

    Article  Google Scholar 

  • Donangelo, R., Fort, H., Dakos, V., Scheffer, M., Van Nes, E.H.: Early warnings for catastrophic shifts in ecosystems: comparison between spatial and temporal indicators. Int. J. Bifurc. Chaos 20(2), 315–321 (2010)

    Article  Google Scholar 

  • Drake, J.M., Griffen, B.D.: Early warning signals of extinction in deteriorating environments. Nature 467, 456–459 (2010)

    Article  Google Scholar 

  • Elger, C.E., Lehnertz, K.: Seizure prediction by non-linear time series analysis of brain electrical activity. Eur. J. Neurosci. 10, 786–789 (1998)

    Article  Google Scholar 

  • Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  • Freidlin, M.I., Wentzell, A.D.: Random Perturbations of Dynamical Systems. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  • Gardiner, C.: Stochastic Methods, 4th edn. Springer, Berlin (2009)

    MATH  Google Scholar 

  • Goldbeter, A., Koshland, D.E.: An amplified sensitivity arising from covalent modification in biological systems. Proc. Natl. Acad. Sci. USA 78, 6840–6844 (1981)

    Article  MathSciNet  Google Scholar 

  • Govaerts, W., Kuznetsov, Yu.A.: Matcont (2010). http://www.matcont.ugent.be/

  • Grasman, J.: Asymptotic Methods for Relaxation Oscillations and Applications. Springer, Berlin (1987)

    Book  MATH  Google Scholar 

  • Gross, T., Sayama, H. (eds.): Adaptive Networks: Theory, Models and Applications. Springer, Berlin (2009)

    Google Scholar 

  • Gross, T., Dommar D’Lima, C.J., Blasius, B.: Epidemic dynamics on an adaptive network. Phys. Rev. Lett. 96, 208701 (2006)

    Article  Google Scholar 

  • Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    MATH  Google Scholar 

  • Guttal, V., Jayaprakash, C.: Impact of noise on bistable ecological systems. Ecol. Model. 201, 420–428 (2007)

    Article  Google Scholar 

  • Hale, J.K.: Ordinary Differential Equations. Dover, New York (2009)

    Google Scholar 

  • Hallerberg, S., Kantz, H.: Influence of the event magnitude on the predictability of extreme events. Phys. Rev. E 77, 011108 (2008)

    Article  MathSciNet  Google Scholar 

  • Hastings, A., Wysham, D.B.: Regime shifts in ecological systems can occur with no warning. Ecol. Lett. 13, 464–472 (2010)

    Article  Google Scholar 

  • Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Springer, Berlin (1981)

    MATH  Google Scholar 

  • Highham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001)

    Article  MathSciNet  Google Scholar 

  • Hong, H., Stein, J.C.: Differences of opinion, short-sales constraints, and market crashes. Rev. Financ. Stud. 16(2), 487–525 (2003)

    Article  Google Scholar 

  • Huang, J., Wang, J.: Liquidity and market crashes. Rev. Financ. Stud. 22(7), 2607–2643 (2008)

    Article  Google Scholar 

  • Imkeller, P., Pavlyukevich, I.: First exit times of SDEs driven by stable Lévy processes. Stoch. Process. Appl. 116(4), 611–642 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  • Izhikevich, E.: Neural excitability, spiking, and bursting. Int. J. Bifurc. Chaos 10, 1171–1266 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  • Jensen, H.J.: Self-Organized Criticality. CUP (1998)

    MATH  Google Scholar 

  • Jones, C.K.R.T.: Geometric singular perturbation theory. In: Dynamical Systems (Montecatini Terme, 1994). Lecture Notes in Mathematics, vol. 1609, pp. 44–118. Springer, Berlin (1995)

    Chapter  Google Scholar 

  • Kabanov, Y., Pergamenshchikov, S.: Two-Scale Stochastic Systems. Springer, Berlin (2003)

    Book  MATH  Google Scholar 

  • Kallenberg, O.: Foundations of Modern Probability, 2nd edn. Springer, New York (2002)

    MATH  Google Scholar 

  • Keeling, M.J., Rand, D.A., Morris, A.J.: Correlation models for childhood epidemics. Proc. R. Soc. B 264(1385), 1149–1156 (1997)

    Article  Google Scholar 

  • Krupa, M., Szmolyan, P.: Extending geometric singular perturbation theory to nonhyperbolic points—fold and canard points in two dimensions. SIAM J. Math. Anal. 33(2), 286–314 (2001a)

    Article  MathSciNet  MATH  Google Scholar 

  • Krupa, M., Szmolyan, P.: Extending slow manifolds near transcritical and pitchfork singularities. Nonlinearity 14, 1473–1491 (2001b)

    Article  MathSciNet  MATH  Google Scholar 

  • Krupa, M., Szmolyan, P.: Geometric analysis of the singularly perturbed fold. In: Multiple-Time-Scale Dynamical Systems. IMA, vol. 122, pp. 89–116 (2001c)

    Chapter  Google Scholar 

  • Krupa, M., Popovic, N., Kopell, N.: Mixed-mode oscillations in three time-scale systems: a prototypical example. SIAM J. Appl. Dyn. Syst. 7(2), 361–420 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  • Kuehn, C.: A mathematical framework for critical transitions: bifurcations, fast-slow systems and stochastic dynamics. Physica D 240(12), 1020–1035 (2011)

    Article  MATH  Google Scholar 

  • Kuehn, C.: Time-scale and noise optimality in self-organized critical adaptive networks. Phys. Rev. E 85(2), 026103-7 (2012)

    Article  MathSciNet  Google Scholar 

  • Kuehn, C., Zschaler, G., Gross, T.: Early warning signs for critical saddle-escape in complex systems. Preprint (2012)

  • Kuske, R.: Probability densities for noisy delay bifurcation. J. Stat. Phys. 96(3), 797–816 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  • Kuznetsov, Yu.A.: Elements of Applied Bifurcation Theory, 3rd edn. Springer, New York (2004)

    Book  MATH  Google Scholar 

  • Lenton, T.M., Held, H., Kriegler, E., Hall, J.W., Lucht, W., Rahmstorf, S., Schellnhuber, H.J.: Tipping elements in the Earth’s climate system. Proc. Natl. Acad. Sci. USA 105(6), 1786–1793 (2008)

    Article  MATH  Google Scholar 

  • Lindner, B., Schimansky-Geier, L.: Analytical approach to the stochastic FitzHugh-Nagumo system and coherence resonance. Phys. Rev. E 60(6), 7270–7276 (1999)

    Article  Google Scholar 

  • Meisel, C., Kuehn, C.: On spatial and temporal multilevel dynamics and scaling effects in epileptic seizures. PLoS ONE 7(2), 1–11 (2012) (e30371)

    Article  Google Scholar 

  • Mishchenko, E.F., Rozov, N.Kh.: Differential Equations with Small Parameters and Relaxation Oscillations. Plenum, New York (1980) (translated from Russian)

    Book  MATH  Google Scholar 

  • Mishchenko, E.F., Kolesov, Yu.S., Kolesov, A.Yu., Rozov, N.Kh.: Asymptotic Methods in Singularly Perturbed Systems. Plenum, New York (1994)

    Book  MATH  Google Scholar 

  • Mormann, F., Andrzejak, R.G., Elger, C.E., Lehnertz, K.: Seizure prediction: the long and winding road. Brain 130, 314–333 (2007)

    Article  Google Scholar 

  • Nagumo, J., Arimoto, S., Yoshizawa, S.: An active pulse transmission line simulating nerve axon. Proc. IRE 50, 2061–2070 (1962)

    Article  Google Scholar 

  • Neishtadt, A.I.: Persistence of stability loss for dynamical bifurcations. I. Differ. Equ. Transl. 23, 1385–1391 (1987)

    MathSciNet  Google Scholar 

  • Neishtadt, A.I.: Persistence of stability loss for dynamical bifurcations. II. Differ. Equ. Transl. 24, 171–176 (1988)

    MathSciNet  Google Scholar 

  • Novak, B., Pataki, Z., Ciliberto, A., Tyson, J.J.: Mathematical model of the cell division cycle of fission yeast. Chaos 11(1), 277–286 (2001)

    Article  MATH  Google Scholar 

  • Øksendal, B.: Stochastic Differential Equations, 5th edn. Springer, Berlin (2003)

    Book  Google Scholar 

  • Perko, L.: Differential Equations and Dynamical Systems. Springer, Berlin (2001)

    MATH  Google Scholar 

  • Rinzel, J.: A formal classification of bursting mechanisms in excitable systems. In: Proc. Int. Congress Math., Berkeley, pp. 1578–1593 (1986)

    Google Scholar 

  • Scheffer, M.: Critical Transitions in Nature and Society. Princeton University Press, Princeton (2009)

    Google Scholar 

  • Scheffer, M., Carpenter, S.R.: Catastrophic regime shifts in ecosystems: linking theory to observation. Trends Ecol. Evol. 18(12), 648–656 (2003)

    Article  Google Scholar 

  • Scheffer, M., Bascompte, J., Brock, W.A., Brovkhin, V., Carpenter, S.R., Dakos, V., Held, H., van Nes, E.H., Rietkerk, M., Sugihara, G.: Early-warning signals for critical transitions. Nature 461, 53–59 (2009)

    Article  Google Scholar 

  • Socha, L.: Linearization Methods for Stochastic Dynamic Systems. Springer, Berlin (2008)

    MATH  Google Scholar 

  • Sowers, R.B.: Random perturbations of canards. J. Theor. Probab. 21, 824–889 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  • Stommel, H.: Thermohaline convection with two stable regimes of flow. Tellus 13, 224–230 (1961)

    Article  Google Scholar 

  • Su, J., Rubin, J., Terman, D.: Effects of noise on elliptic bursters. Nonlinearity 17, 133–157 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Szmolyan, P., Wechselberger, M.: Canards in ℝ3. J. Differ. Equ. 177, 419–453 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  • Thompson, J.M.T., Sieber, J.: Climate tipping as a noisy bifurcation: a predictive technique. IMA J. Appl. Math. 76(1), 27–46 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  • Touboul, J., Wainrib, G.: Bifurcations of stochastic differential equations with singular diffusion coefficients, pp. 1–39 (2012). arXiv:1205.0172v1

  • Tyson, J.J., Chen, K.C., Novak, B.: Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. In: Current Opinion in Cell Biology, vol. 15, pp. 221–231 (2003)

    Google Scholar 

  • van Gils, S., Krupa, M., Langford, W.F.: Hopf bifurcation with non-semisimple 1:1 resonance. Nonlinearity 3, 825–850 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  • van Nes, E.H., Scheffer, M.: Slow recovery from perturbations as generic indicator of a nearby catastrophic shift. Am. Nat. 169(6), 738–747 (2007)

    Article  Google Scholar 

  • Venegas, J.G., Winkler, T., Musch, G., Vidal Melo, M.F., Layfield, D., Tgavalekos, N., Fischman, A.J., Callahan, R.J., Bellani, G., Harris, R.S.: Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature 434, 777–782 (2005)

    Article  Google Scholar 

  • Venkadesan, M., Guckenheimer, J., Valero-Cuevas, F.J.: Manipulating the edge of instability. J. Biomech. 40, 1653–1661 (2007)

    Article  Google Scholar 

  • Veraart, A.J., Faassen, E.J., Dakos, V., van Nes, E.H., Lurling, M., Scheffer, M.: Recovery rates reflect distance to a tipping point in a living system. Nature 481, 357–359 (2012)

    Google Scholar 

  • Wiggins, S.: Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd edn. Springer, New York (2003)

    MATH  Google Scholar 

  • Wolfram Research Inc.: Mathematica Edition: Version 8.0 (2010). Wolfram Research, Inc.

    Google Scholar 

  • Zagaris, A., Kaper, H.G., Kaper, T.J.: Analysis of the computational singular perturbation method for chemical kinetics. J. Nonlinear Sci. 14, 59–91 (2004)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

I would like to thank Martin Zumsande for suggesting the model from systems biology in Sect. 7.3 and Thilo Gross for insightful discussions regarding network dynamics. I also would like to thank two anonymous referees and the editor for many helpful comments that helped to improve the manuscript. Part of this work was supported by the European Commission (EC/REA) via a Marie-Curie International Re-integration Grant.

Author information

Authors and Affiliations

  1. Max Planck Institute, Physics of Complex Systems, Dresden, 01187, Germany

    Christian Kuehn

  2. Institute for Analysis and Scientific Computing, Vienna University of Technology, Vienna, 1040, Austria

    Christian Kuehn

Authors
  1. Christian Kuehn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christian Kuehn.

Additional information

Communicated by Philip Holmes.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kuehn, C. A Mathematical Framework for Critical Transitions: Normal Forms, Variance and Applications. J Nonlinear Sci 23, 457–510 (2013). https://doi.org/10.1007/s00332-012-9158-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00332-012-9158-x

Keywords

Mathematics Subject Classification

Search

Navigation