Open problems in PDE models for knowledge-based animal movement via nonlocal perception and cognitive mapping

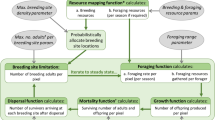
Abstract

The inclusion of cognitive processes, such as perception, learning and memory, are inevitable in mechanistic animal movement modelling. Cognition is the unique feature that distinguishes animal movement from mere particle movement in chemistry or physics. Hence, it is essential to incorporate such knowledge-based processes into animal movement models. Here, we summarize popular deterministic mathematical models derived from first principles that begin to incorporate such influences on movement behaviour mechanisms. Most generally, these models take the form of nonlocal reaction-diffusion-advection equations, where the nonlocality may appear in the spatial domain, the temporal domain, or both. Mathematical rules of thumb are provided to judge the model rationality, to aid in model development or interpretation, and to streamline an understanding of the range of difficulty in possible model conceptions. To emphasize the importance of biological conclusions drawn from these models, we briefly present available mathematical techniques and introduce some existing “measures of success” to compare and contrast the possible predictions and outcomes. Throughout the review, we propose a large number of open problems relevant to this relatively new area, ranging from precise technical mathematical challenges, to more broad conceptual challenges at the cross-section between mathematics and ecology. This review paper is expected to act as a synthesis of existing efforts while also pushing the boundaries of current modelling perspectives to better understand the influence of cognitive movement mechanisms on movement behaviours and space use outcomes.

Appendices

Appendix

A Equivalence of Models

In some cases, the models presented in this review can be reformulated into an equivalent model. We first write the full problem studied in Shi et al. (2019):

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t} = d_1 \Delta u + d_2 \nabla \cdot ( u \nabla v) + f(u), \quad \ \, x \in \Omega , \ t>0, \\ \frac{\partial u}{\partial {\textbf{n}}} = 0 , \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\, x \in \partial \Omega , \ t>0, \\ u(x,t) = \eta (x,t), \qquad \qquad \qquad \qquad \qquad \,\,\, x \in \Omega , \ -\infty < t \le 0, \end{array}\right. } \end{aligned}$$

(A.1)

in a smooth, bounded domain $\Omega$, $\eta (x,t)$ is given initial data, and v(x, t) is defined as

$$\begin{aligned} v(x,t) = {\mathcal {G}} ** u = \int _{- \infty } ^t \int _\Omega G(d_3, x,y,t-s) {\mathcal {G}}(t-s) u(y,s) dy ds , \end{aligned}$$

where G is the Green’s function for the heat equation in $\Omega$ subject to homogeneous Neumann boundary data, $d_3$ is the diffusion rate for the Green’s function, and ${\mathcal {G}}$ is either the weak or strong kernel defined in (2.27). We first state Lemma 2.1 found in Shi et al. (2021). The lemma is stated as follows.

Lemma A.1

Suppose that kernel ${\mathcal {G}}_w(t)$ is chosen to be the weak kernel defined in (2.27) and define

$$\begin{aligned} v(x,t) = {\mathcal {G}}_w ** u(x,t) = \int _{-\infty }^t \int _\Omega G(d_3,x,y,t-s) {\mathcal {G}}_w (t-s) u(y,s) dy ds, \end{aligned}$$

where G is the Green’s function for the heat equation subject to homogeneous Neumann boundary data. Then,

• 1. If u(x, t) is the solution of (A.1), then (u(x, t), v(x, t)) is the solution of

  $$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t} = d_1 \Delta u + d_2 \nabla \cdot ( u \nabla v) + f(u), \quad \quad x \in \Omega , \ t>0, \\ \frac{\partial v}{\partial t} = d_3 \Delta v + \tau ^{-1} ( u - v), \qquad \qquad \qquad \quad x \in \Omega ,\ t>0, \\ \frac{\partial u}{\partial {\textbf{n}}} = \frac{\partial v}{\partial {\textbf{n}}} = 0 , \qquad \qquad \qquad \qquad \qquad \qquad \quad \,\,\,\, x \in \partial \Omega , \ t>0, \\ u(x,t) = \eta (x,t), \qquad \qquad \qquad \qquad \qquad \quad \,\,\,\, x \in \Omega , \ t \le 0, \\ v(x,0) = \tau ^{-1} \int _{-\infty }^0 \int _\Omega G(x,y,-s) e^{s \tau ^{-1}} \eta (y,s) dy ds. \end{array}\right. } \end{aligned}$$

  (A.2)

• 2. If (u(x, t), v(x, t)) is a solution of

  $$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t} = d_1 \Delta u + d_2 \nabla \cdot ( u \nabla v) + f(u), \quad \quad \qquad x \in \Omega ,\ t\in {\mathbb {R}}, \\ \frac{\partial v}{\partial t} = d_3 \Delta v + \tau ^{-1}(u-v), \qquad \qquad \qquad \qquad \,\,\,\, x \in \Omega , \ t\in {\mathbb {R}}, \\ \frac{\partial u}{\partial {\textbf{n}}} = \frac{\partial v}{\partial {\textbf{n}}} = 0 , \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \,\,\,\, x \in \partial \Omega , \ t\in {\mathbb {R}}, \end{array}\right. } \end{aligned}$$

  (A.3)

  then u(x, t) satisfies equation (A.1) such that $\eta (x,s) = u(x,s)$, $-\infty< s < 0$. In particular, if (u(x), v(x)) is a steady state of (A.3), then u(x) is a steady state of (A.1); if (u(x, t), v(x, t)) is a periodic solution of (A.3), then u(x, t) is a periodic solution of (A.1).

This is an interesting result for two reasons. First, it is interesting to see that model (A.1) is actually equivalent to a Keller-Segel chemotaxis model when the weak kernel is chosen. Second, as a result of this first fact, one can then use the huge body of literature studying chemotaxis models in order to gain insights into this new delay partial differential equation. In the case where one chooses the strong kernel, there is another equivalent system consisting of 3 equations and similar insights can be gathered. This is Lemma 2.2 in Shi et al. (2021), which we do not provide here.