Revisiting Shao and Sokal’s B₂ index of phylogenetic balance

Abstract

Measures of phylogenetic balance, such as the Colless and Sackin indices, play an important role in phylogenetics. Unfortunately, these indices are specifically designed for phylogenetic trees, and do not extend naturally to phylogenetic networks (which are increasingly used to describe reticulate evolution). This led us to consider a lesser-known balance index, whose definition is based on a probabilistic interpretation that is equally applicable to trees and to networks. This index, known as the $B_2$ index, was first proposed by Shao and Sokal (Syst Zool 39(3): 266–276, 1990). Surprisingly, it does not seem to have been studied mathematically since. Likewise, it is used only sporadically in the biological literature, where it tends to be viewed as arcane. In this paper, we study mathematical properties of $B_2$ such as its expectation and variance under the most common models of random trees and its extremal values over various classes of phylogenetic networks. We also assess its relevance in biological applications, and find it to be comparable to that of the Colless and Sackin indices. Altogether, our results call for a reevaluation of the status of this somewhat forgotten measure of phylogenetic balance.

Appendix

1.1 A.1 Variance of $B_2$ in binary Galton–Watson trees

In this section, we prove Proposition 3.3 concerning the variance of $B_2$ in binary Galton–Watson trees. Let us start with a standard result, which we recall and prove for the sake of completeness.

Lemma A.1.1

Let $(Z_t)$ be a Galton–Watson process with offspring distribution $Y \sim 2\, \mathrm {Bernoulli(1/2)}$. Then, ${\mathbb {E}}\!\left( {Z_t^2}\right) = t + 1$.

Proof

Since $Z_{t + 1} = \sum _{i = 1}^{Z_t} Y_t(i)$, we have

$$\begin{aligned} Z_{t + 1}^2 \;=\; \sum _{i = 1}^{Z_t} Y_t(i)^2 \;+\; \sum _{i = 1}^{Z_t} \sum _{j \ne i}^{Z_t} Y_t(i)\, Y_t(j)\,. \end{aligned}$$

Letting ${\mathcal {F}}_t$ be the natural filtration of the process, we thus have

$$\begin{aligned} {\mathbb {E}}\!\left( {Z_{t + 1}^2 \,|\,{\mathcal {F}}_t}\right) \;=\; {\mathbb {E}}\!\left( {Y^2}\right) \,Z_t \;+\; {\mathbb {E}}\!\left( {Y}\right) ^2 \, Z_t(Z_t - 1) \end{aligned}$$

and, as a result,

$$\begin{aligned} {\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) \;=\; {\mathbb {E}}\!\left( {Y^2}\right) \,{\mathbb {E}}\!\left( {Z_t}\right) \;+\; {\mathbb {E}}\!\left( {Y}\right) ^2 \, {\mathbb {E}}\!\left( {Z_t^2}\right) \;-\; {\mathbb {E}}\!\left( {Y}\right) ^2 \, {\mathbb {E}}\!\left( {Z_t}\right) \,. \end{aligned}$$

Since here ${\mathbb {E}}\!\left( {Y}\right) = 1$, ${\mathbb {E}}\!\left( {Y^2}\right) = 2$ and ${\mathbb {E}}\!\left( {Z_t}\right) = 1$, this simplifies to

$$\begin{aligned} {\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) \;=\; {\mathbb {E}}\!\left( {Z_t^2}\right) \;+\; 1\,. \end{aligned}$$

The lemma then follows by induction, since ${\mathbb {E}}\!\left( {Z_0^2}\right) = 1$. $\square$

Let us now recall Proposition 3.3 and prove it.

Proposition 3.3

Let T be a critical binary Galton–Watson tree, that is, assume that the offspring distribution is ${\mathbb {P}}\!\left( {Y = 0}\right) = {\mathbb {P}}\!\left( {Y = 2}\right) = 1/2$. Then,

$$\begin{aligned} \mathrm {Var}\!\left( {B_2(T_{[t]})}\right) \;=\; \frac{4}{3} - 2^{-t+2} + 4^{-t}\left( t + \frac{8}{3}\right) \,. \end{aligned}$$

Proof

To alleviate the notation, let us write $B_t = B_2(T_{[t]})$. With this notation, since in the case of a binary Galton–Watson tree ${\mathbb {1}}_{\{Y_t > 0\}} = Y_t / 2$, Equation (3) from the proof of Theorem 3.1 becomes

$$\begin{aligned} B_{t + 1} \;=\; B_t \;+\; 2^{-(t + 1)} \sum _{i = 1}^{Z_t} Y_t(i) \,. \end{aligned}$$

(A.1)

Therefore, letting ${\mathcal {F}}_t$ denote the natural filtration of the process and using that ${\mathbb {E}}\!\left( {Y}\right) = 1$, we have

$$\begin{aligned} {\mathbb {E}}\!\left( {\left. B_{t + 1}^2 \right| {\mathcal {F}}_t}\right) \;=\; B_t^2 \;+\; 2^{-t} B_t\, Z_t \;+\; 2^{-2(t + 1)} \, {\mathbb {E}}\!\left( {\left. Z_{t + 1}^2 \right| {\mathcal {F}}_t}\right) . \end{aligned}$$

As a result,

$$\begin{aligned} {\mathbb {E}}\!\left( {B_{t + 1}^2}\right) \;=\; {\mathbb {E}}\!\left( {B_t^2\,}\right) \;+\; 2^{-t} \,{\mathbb {E}}\!\left( {B_t Z_t}\right) \;+\; 2^{-2(t + 1)} \, {\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) . \end{aligned}$$

(A.2)

Let us now turn our attention to ${\mathbb {E}}\!\left( {B_t Z_t}\right)$. Using Equation (A.1), we get

$$\begin{aligned} B_{t+1} Z_{t + 1} \;&=\; \left( B_t + 2^{-(t + 1)} Z_{t + 1}\right) Z_{t+1} \\ \;&=\; B_t \sum _{i = 1}^{Z_t} Y_t(i) \;+\; 2^{-(t + 1)} Z_{t + 1}^2 \,, \end{aligned}$$

and since ${\mathbb {E}}\!\left( {\left. B_t \sum _{i = 1}^{Z_t} Y_t(i) \right| {\mathcal {F}}_t}\right) = B_t Z_t$ this yields

$$\begin{aligned} {\mathbb {E}}\!\left( {B_{t+1} Z_{t + 1}}\right) \;=\; {\mathbb {E}}\!\left( {B_t Z_t}\right) \;+\; 2^{-(t + 1)} {\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) \,. \end{aligned}$$

By Lemma A.1.1, ${\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) = t + 2$. Since ${\mathbb {E}}\!\left( {B_0 Z_0}\right) = 0$, we thus have

$$\begin{aligned} {\mathbb {E}}\!\left( {B_t Z_t}\right) \;=\; \sum _{s = 0}^{t - 1} 2^{-(s + 1)} (s + 2) \;=\; 3 - 2^{-t}(t + 3)\,. \end{aligned}$$

Plugging this and ${\mathbb {E}}\!\left( {Z_{t + 1}^2}\right) = t + 2$ in Equation (A.2), we get the following closed recurrence relation for ${\mathbb {E}}\!\left( {B_t^2}\right)$:

$$\begin{aligned} {\mathbb {E}}\!\left( {B_{t + 1}^2}\right) \;=\; {\mathbb {E}}\!\left( {B_t^2\,}\right) \;+\; 2^{-t} \,\big (3 - 2^{-t}(t + 3)\big ) \;+\; 2^{-2(t + 1)} \, (t + 2). \end{aligned}$$

Solving this recurrence relation with the initial condition ${\mathbb {E}}\!\left( {B_0^2}\right) = 0$ then yields

$$\begin{aligned} {\mathbb {E}}\!\left( {B_t^2\,}\right) \;=\; \frac{7}{3} - 6\cdot 2^{-t} + 4^{-t}\left( t + \frac{11}{3}\right) \,. \end{aligned}$$

Finally, since by Theorem 3.1, ${\mathbb {E}}\!\left( {B_t}\right) = 1 - 2^{-t}$, we have

$$\begin{aligned} \mathrm {Var}\!\left( {B_t}\right) \;=\; \frac{4}{3} - 4\cdot 2^{-t} + 4^{-t}\left( t + \frac{8}{3}\right) \,, \end{aligned}$$

concluding the proof. $\square$

1.2 A.2 Bounds on the number of distinct values of $B_2$

Proposition A.2.2

Let ${\mathscr {T}}_n$ denote the set of rooted binary trees with n leaves, labeled or unlabeled. Then,

$$\begin{aligned} 2^{\lfloor {n/2}\rfloor - 1} \;\le \; \# B_2({\mathscr {T}}_n) \;\le \; a_n \end{aligned}$$

where $a_n$ is sequence A002572 in Online Encyclopedia of Integer Sequences (2020) and satisfies $a_n \sim K \rho ^n$, with $\rho \approx 1.7941$ and $K \approx 0.2545$ the Flajolet–Prodinger constant.

Proof

The upper bound is obtained by noting that $B_2(T)$ is a function of the multiset of the depths of the leaves of the binary tree T. Therefore, $B_2$ cannot take more values than the number $a_n$ of such multisets, whose asymptotics were characterized by Flajolet and Prodinger in Flajolet and Prodinger (1987).

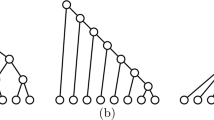
To obtain the lower bound, we exhibit $2^{\lfloor {n/2}\rfloor - 1}$ rooted binary trees with n leaves whose $B_2$ indices are different. For any integer m and any ${\mathbf {x}} \in \{0, 1\}^m$, let $T({\mathbf {x}})$ denote the ordered (that is, embedded in the plane) rooted binary tree obtained by the following sequential construction: starting from the binary tree with two leaves, for $k = 1, \ldots , m$,

• If $x_k = 0$, graft a cherry on the left-most leaf with depth k.

• If $x_k = 1$, graft a cherry on each of the two left-most leaves with depth k.

This construction is illustrated in Fig. 11.

Fig. 11

The trees $T({\mathbf {x}})$ for $m \in \{0, 1, 2\}$. Each tree is represented with the corresponding vector ${\mathbf {x}} \in \{0, 1\}^m$ on the right

Clearly, $T({\mathbf {x}})$ has $2 + \sum _{k = 1}^{m} (x_k + 1)$ leaves and, by Corollary 1.11,

$$\begin{aligned} B_2(T({\mathbf {x}})) \;=\; 1 \;+\; \sum _{k = 1}^{m} (x_k + 1)\, 2^{-k} \,. \end{aligned}$$

As a result,

$$\begin{aligned} \big \{B_2(T({\mathbf {x}})) \,:\,{\mathbf {x}} \in \{0, 1\}^m\big \} \;=\; \{u_m + i\, 2^{-m} : i = 0, \ldots , 2^m - 1\} \end{aligned}$$

(to see this, note that $B_2(T({\mathbf {x}})) = u_m + \underline{{\mathbf {x}}}_{(2)}$, where $\underline{{\mathbf {x}}}_{(2)} = \sum _{k} x_k 2^{-k}$ denotes the dyadic rational of $[{0, 1}[$ whose binary expansion is ${\mathbf {x}}$). Thus, this construction generates $2^m$ trees whose $B_2$ indices differ by at least $2^{-m}$. However, these trees do not have the same number of leaves.

Let us first assume that n is even. Then, with $m = n/2 - 1$, $T(1\cdots 1)$ has n leaves and every other tree $T({\mathbf {x}})$ with ${\mathbf {x}} \in \{0, 1\}^m$ has:

• (i) $n - k_{\mathbf {x}}$ leaves, with $1 \le k_{\mathbf {x}} \le m$;

• (ii) its left-most leaf at depth $m + 1$.

Now, if we graft a caterpillar with $k_{\mathbf {x}} + 1$ leaves on the left-most leaf at depth $m + 1$ and let $T'({\mathbf {x}})$ denote the resulting tree, then:

($\mathrm {i}^\prime$):

$T'({\mathbf {x}})$ has n leaves;

($\mathrm {ii}^\prime$):

by Proposition 1.10, $B_2(T'({\mathbf {x}})) - B_2(T({\mathbf {x}})) = 2^{-(m+1)}(2 - 2^{-k+1}) \in ]{0, 2^{-m}}[$.

Since the $B_2$ indices of the trees $T({\mathbf {x}})$ differ by at least $2^{-m}$, by point ($\mathrm {ii}^\prime$) the $B_2$ indices of the trees $T'({\mathbf {x}})$ are all different, thereby proving the proposition in the case where n is even.

If n is odd, do the same construction, again with $m = \lfloor n / 2\rfloor - 1$, to get $2^m$ trees with $n - 1$ leaves. Then, for each of these trees, graft a cherry on the sibling of the left-most vertex at depth $m + 1$ (which exists and is always a leaf). This extra step increases $B_2$ by the same amount $2^{-(m + 1)}$ for every tree, concluding the proof. $\square$