On the steady state optimization of the biogas production in a two-stage anaerobic digestion model

Abstract

In this paper, we study the optimization problem of maximizing biogas production at steady state in a two-stage anaerobic digestion model, which was initially proposed in Bernard et al. (Biotechnol Bioeng 75(4):424–438, 2001). Nominal operating points, consisting of steady states where the involved microorganisms coexist, are usually referred to as desired operational conditions, in particular for maximizing biogas production. Nevertheless, we prove that under some conditions related to input substrate concentrations and microorganism biology, characterized by their growth functions, the optimal steady state can be the extinction of one of the two species. We provide some numerical examples of this situation.

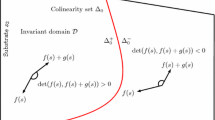
Appendix: Expressions of curves \(C_1\)–\(C_2\)–\(C_3\) for Monod and Haldane kinetics

In the AM2 model (Bernard et al. 2001), recall that ${\tilde{\mu }}_1$ and ${\tilde{\mu }}_2$ are Monod and Haldane respectively (see Example 1). We can then explicit the expressions defining the curves $C_2$ and $C_3$ given by (23)–(24) as follows. A preliminary inspection allows us to find that for Monod’s kinetics, one has

$$\begin{aligned} {\tilde{\mu }}_1(S_{in}^1)= \frac{{\bar{\mu }}_1 S_{in}^1}{k_A+S_{in}^1}\quad \mathrm {and} \quad \frac{{\tilde{\mu }}_1(S_{in}^1)}{{\tilde{\mu }}_1'(S_{in}^1)}=\frac{(k_A+S_{in}^1)S_{in}^1}{k_A}. \end{aligned}$$

For Haldane’s kinetics, $S_2^*(u)$ is the lowest (positive) solution to the equation ${\tilde{\mu }}_2(S_2)=u$. It is easily seen that $S_2^*(u)$ is the lowest root of a quadratic equation. This gives:

$$\begin{aligned} {} S_2^*(u):=\frac{k_I({\bar{\mu }}_2 -u) - \sqrt{{\varDelta }(u)}}{2u} \quad \mathrm {with} \quad {\varDelta }(u):=({\bar{\mu }}_2-u)^2 k_I^2 - 4k_M k_I u^2. \end{aligned}$$

(25)

The number $S_2^*(u)$ is well defined provided that $u>0$ and ${\varDelta }(u)>0$. In addition, differentiating the previous expression w.r.t. u gives

$$\begin{aligned} {} S_2^{* '}(u)=\frac{{\bar{\mu }}_2 k_I^2({\bar{\mu }}_2 -u) - \sqrt{{\varDelta }(u)}}{2u^2\sqrt{{\varDelta }(u)}}. \end{aligned}$$

(26)

For the curve $C_2$, we can then conclude that a point $(S_{in}^1,S_{in}^2)\in C_2$ whenever:

$$\begin{aligned} S_{in}^2=S_2^*({\tilde{\mu }}_1(S_{in}^1))+\frac{{\bar{\mu }}_1 S_{in}^1 S_2^{* '}({\tilde{\mu }}_1(S_{in}^1))}{k_A+S_{in}^1}, \end{aligned}$$

since ${\tilde{\mu }}_2(S_2^*(u))S_2^{* '}(u)=1$. Similarly a point $(S_{in}^1,S_{in}^2)$ belongs to $C_3$ whenever

$$\begin{aligned} S_{in}^2=S_2^*({\tilde{\mu }}_1(S_{in}^1))+\frac{k_2S_{in}^1(k_A+S_{in}^1)}{k_1k_A}+\frac{{\bar{\mu }}_1 S_{in}^1 S_2^{* '}({\tilde{\mu }}_1(S_{in}^1)) }{k_A+S_{in}^1}. \end{aligned}$$

These expressions are well defined because one has ${\tilde{\mu }}_1(S_{in}^1)<{\tilde{\mu }}_2({\tilde{S}}_2)$, and they define the curves $C_2$ and $C_3$ respectively.