Exploring the space of gene/species reconciliations with transfers

Abstract

Reconciliations between gene and species trees have important applications in the study of genome evolution (e.g. sequence orthology prediction or quantification of transfer events). While numerous methods have been proposed to infer them, little has been done to study the underlying reconciliation space. In this paper, we characterise the reconciliation space for two evolutionary models: the $\mathbb {DTL}$ (duplication, loss and transfer) model and a variant of it—the no-$\mathbb {TL}$ model—which does not allow $\mathbb {TL}$ events (a transfer immediately followed by a loss). We provide formulae to compute the size of the corresponding spaces and define a set of transformation operators sufficient to explore the entire reconciliation space. We also define a distance between two reconciliations as the minimal number of operations needed to transform one into the other and prove that this distance is easily computable in the no-$\mathbb {TL}$ model. Computing this distance in the $\mathbb {DTL}$ model is more difficult and it is an open question whether it is NP-hard or not. This work constitutes an important step toward reconciliation space characterisation and reconciliation comparison, needed to better assess the performance of reconciliation inference methods through simulations.

Appendices

Appendix A: A reconciliation counting example

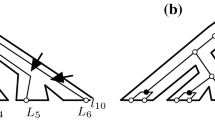
We illustrate Theorem 1 by counting the number of reconciliations between the trees shown in Fig. 1. It is trivial to calculate $R(l,z)$ for $l \in L(G)$, so we do not illustrate this. In Fig. 9a, we calculate $R(v,z)$ for all elements $z$ of $S'$; when this number is non-zero, it is written in the tree at $z$ next to a symbol indicating the type of event that $v$ is mapped to—in accordance with convention we use circles, squares and triangles for $\mathbb {S}$, $\mathbb {D}$ and $\mathbb {T}$ events respectively. For example, $R(v,x) = 1$, and if $v$ is mapped to $x$ it must be an $\mathbb {S}$ event. Because $v_l$ and $v_r$ are both leaves, $R(v,z)$ is at most 1 for any $z$. In Fig. 9b, we do likewise with $R(w,z)$ for all elements $z$ of $S'$.

In Fig. 9c, we calculate $R(u,z)$ for all elements $z$ of $S'$ in the same fashion. Here, if $u$ can be mapped as two different events in the same branch, we separate the cases (for clarity) even though they are added together in $R(u,z)$. For example, suppose $z = e(y)$. Here, if $u$ is mapped to $z$ as a $\mathbb {T}$ event, then the branch containing $v$ must be the transferred branch. From Fig. 9a, there are 2 possible images for $v$ that are allowed by $z$ but not below it, and for each of these images (called, say, $z'$) $R(v,z') = 1$. Likewise, from Fig. 9b there are 4 possible images for $w$ that are below $z$, and each of these images again have $R(w,z') = 1$. Thus there are 8 possibilities for $u$ to be mapped to $z$ as a $\mathbb {T}$ event. It can be determined likewise that there are also 8 possibilities for $u$ to be mapped to $z$ as a $\mathbb {D}$ event, and so $R(u,z) = 16$.

The total number of reconciliations is found by summing all the possibilities in all branches of Fig. 9c, which gives a total of 70 reconciliations.

Fig. 9

Counting the number of reconciliations between the trees in Fig. 1. a All possible placements for vertex $v$. Each placement has 1 possibility. b All possible placements for vertex $w$. Each placement has 1 possibility. c All possible placements for vertex $u$. The number of possibilities is indicated

Appendix B: Reconciliation definitions

In this section, we reproduce (for completeness) the formal definitions of a $\mathbb {DTL}$ reconciliation and a canonical reconciliation in Scornavacca et al. (2013).

Definition 15

(Definition 1, Scornavacca et al. 2013) Consider a gene tree $G$, a dated species tree $S$ such that $\mathcal {L}{(G)} \subseteq \mathcal {L}{(S)}$, and its subdivision $S'$. Let $\alpha$ be a function that maps each node $u$ of $G$ onto an ordered sequence of nodes of $S'$, denoted $\alpha (u)=(\alpha _1(u), \alpha _2(u), \ldots , \alpha _\ell (u))$. The function $\alpha$ is said to be a reconciliation between $G$ and $S'$ if and only if exactly one of the following events occurs for each couple of nodes $u$ of $G$ and $\alpha _i(u)$ of $S'$ (denoting $\alpha _i(u)$ by $x'$ below):

• a) if $x'$ is the last node of $\alpha (u)$, one of the cases below is true:

  • 1. $u \in L(G), x' \in L(S')$ and $s(x')=s(u)$;                                                        $($ $\mathbb {C}$ event$)$

  • 2. $\{\alpha _1(u_l), \alpha _1(u_r)\} =\{x'_l,x'_r\}$;                                                                          $($ $\mathbb {S}$ event$)$

  • 3. $\alpha _1(u_l)=x'$ and $\alpha _1(u_r)=x'$;                                                                         $($ $\mathbb {D}$ event$)$

  • 4. $\alpha _1(u_l)=x'$, and $\alpha _1(u_r)$ is any node other than $x'$ having height $h(x')$

    or $\alpha _1(u_r)=x'$, and $\alpha _1(u_l)$ is any node other than $x'$ having height $h(x')$;    $($ $\mathbb {T}$ event$)$

• b) otherwise, one of the cases below is true:

  • 5. $x'$ is an artificial node and $\alpha _{i+1}(u)$ is its only child;                         $($ $\varnothing$ event$)$

  • 6. $x'$ is not artificial and $\alpha _{i+1}(u) \in \{x'_l,x'_r\}$;                                       $($ $\mathbb {SL}$ event$)$

  • 7. $\alpha _{i+1}(u)$ is any node other than $x'$ having height $h(x')$.                    $($ $\mathbb {TL}$ event$)$

Definition 16

(Definition 2, Scornavacca et al. 2013) Consider a gene tree $G$, a dated species tree $S$ such that $\mathcal {L}{(G)} \subseteq \mathcal {L}{(S)}$, and its subdivision $S'$. A reconciliation $\alpha$ between $G$ and $S'$ is said to be canonical if and only if:

• 1. for each node $u$ of $G$ and index $1 \le i \le |\alpha (u)|$, the node $\alpha _i(u)$ satisfies one of the following conditions:

  • (a) $\alpha _i(u)$ is a $\mathbb {C}$/$\mathbb {S}$/$\varnothing$/$\mathbb {SL}$ event;

  • (b) $\alpha _i(u)$ is a $\mathbb {D}$/$\mathbb {T}$ event such that at least one of $\alpha _1(u)$ and $\alpha _1(u_r)$ is not a $\varnothing$ event;

  • (c) $\alpha _i(u)$ is a $\mathbb {TL}$ event such that $\alpha _i(u)$ is a non-artificial node of $S'$ or $\alpha _{i+1}(u)$ is not a $\varnothing$ event.

• 2. $\alpha _1(r(G))$ is not a $\varnothing$ event.

Appendix C: Distance measure induced by $UP$ and $DOWN$ operators

Definition 17

Let $\alpha$ and $\beta$ be two reconciliations. We define $d^v(\alpha ,\beta )$ to be the smallest number of $UP$ and $DOWN$ operators needed to transform $\alpha$ into $\beta$ (combined with any number of $PATH$ and $OUT$ operators).

It is possible that $d^v(\alpha ,\beta )$ may in fact be less than the number of $UP$ and $DOWN$ operators in the overall shortest sequence of operators. We note that it is certainly a lower bound for this number.

Definition 18

Let $\alpha$ and $\beta$ be two reconciliations. The midpoint mapping $\hat{\gamma }$ of $\alpha$ and $\beta$ is a mapping $V(G) \rightarrow V(S) \cup E(S')$ where, for all $u \in V(G), \hat{\gamma }(u)$ is above both $\bar{\alpha }(u)$ and $\bar{\beta }(u)$, and if $u$ is an internal vertex, $\hat{\gamma }(u)$ allows $\hat{\gamma }(u_l)$ and $\hat{\gamma }(u_r)$. Furthermore, there exists no reconciliation $\gamma '$ with a vertex mapping $\bar{\gamma '}$ which satisfies these properties and where $\bar{\gamma '}(u) \le \hat{\gamma }(u)$ for all $u \in V(G)$ and the inequality is strict in at least one case.

By definition, the midpoint mapping is a valid vertex mapping, so there exists at least one reconciliation with vertex mapping equal to $\hat{\gamma }$.

Definition 19

Let $\alpha$ and $\beta$ be two reconciliations. The midpoint $\gamma$ of $\alpha$ and $\beta$ is a reconciliation with vertex mapping $\bar{\gamma } = \hat{\gamma }$. This specifies $\gamma _\ell (u)$ for all $u \in V(G)$. For each internal vertex $u$ of $G$, we then choose:

• if $\hat{\gamma }(u) \in V(S)$, then $\gamma _1(u_l) = (\gamma _\ell (u))_l$ and $\gamma _1(u_r) = (\gamma _\ell (u))_r$;

• if $\hat{\gamma }(u) \in E(S')$, then $\gamma _1(u_l) = \gamma _1(u_r) = \gamma _\ell (u)$ (a $\mathbb {D}$ event),

and take $\gamma _1(r(G)) = \gamma _\ell (r(G))$. We take the remaining values of $\gamma (u)$ as specified in the proof of Lemma 4.

Theorem 7

Let $\alpha$ and $\beta$ be two reconciliations with midpoint $\gamma$. Let $d^v_u(\alpha , \gamma )$ be the number of edges and non-artificial vertices that lie between $\bar{\alpha }(u)$ and $\bar{\gamma }(u)$. Then

$$\begin{aligned} d^v(\alpha ,\beta ) = d^v(\alpha ,\gamma ) + d^v(\gamma ,\beta ) = \sum _{u \in V(G)} d^v_u(\alpha ,\gamma ) + \sum _{u \in V(G)} d^v_u(\beta , \gamma ). \end{aligned}$$

Proof

The reasoning used in the first three paragraphs of the proof of Theorem 3 can be used again here, replacing “reconciliation” by “vertex mapping”, to show that for any vertex $u$, in any sequence of reconciliations transforming $\alpha$ to $\beta$, at least one must have a vertex mapping which maps $u$ to $\bar{\gamma }(u)$.

Because an $UP_u$ operator will only move the vertex mapping of $u$ to its nearest non-artificial ancestor, it is clear that we require at least $d^v_u(\alpha ,\gamma )$ such operators to reach a reconciliation with a vertex mapping which maps $u$ to $\bar{\gamma }(u)$. Likewise, we require at least $d^v_u(\beta ,\gamma ) DOWN_u$ operators to go from this reconciliation to one with a vertex mapping which maps $u$ to $\bar{\beta }(u)$. Therefore we have

$$\begin{aligned} d^v(\alpha ,\beta ) \ge \sum _{u \in V(G)} d^v_u(\alpha ,\gamma ) + \sum _{u \in V(G)} d^v_u(\beta , \gamma ). \end{aligned}$$

It remains to show that there is a valid sequence of operators with this many $UP$ and $DOWN$ operators which transforms $\alpha$ to $\beta$. Consider the sequence which starts from $\alpha$ and applies $UP$ operators to each internal vertex $u$ of $G$ in pre-order until it is mapped (via the vertex mapping) to $\bar{\gamma }(u)$. This is always possible because $\bar{\gamma }$ is a valid vertex mapping and so $\bar{\gamma }(u)$ allows $\bar{\gamma }(u_l)$ and $\bar{\gamma }(u_r)$. By Corollary 2, we can apply only $PATH$ and $OUT$ operators to transform the resulting reconciliation into $\gamma$. This requires exactly $\sum _{u \in V(G)} d^v_u(\alpha ,\gamma ) UP$ operators.

Now we can apply a similar procedure to $\gamma$, applying $DOWN$ operators in post-order (choosing $DOWN^l$ and $DOWN^r$ appropriately) until each vertex $u$ is mapped (via the vertex mapping) to $\bar{\beta }(u)$. As before, this is always possible, and we then apply $PATH$ and $OUT$ operators to transform the resulting reconciliation into $\beta$. This requires exactly $\sum _{u \in V(G)} d^v_u(\beta , \gamma ) DOWN$ operators, and so the sequence we describe is the required sequence.$\square$