Alzheimer’s disease: analysis of a mathematical model incorporating the role of prions

Abstract

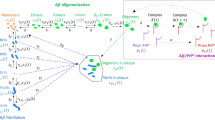
We introduce a mathematical model of the in vivo progression of Alzheimer’s disease with focus on the role of prions in memory impairment. Our model consists of differential equations that describe the dynamic formation of $\upbeta$-amyloid plaques based on the concentrations of A$\upbeta$ oligomers, PrP^C proteins, and the A$\upbeta$-$\times$-PrP^Ccomplex, which are hypothesized to be responsible for synaptic toxicity. We prove the well-posedness of the model and provided stability results for its unique equilibrium, when the polymerization rate of $\upbeta$-amyloid is constant and also when it is described by a power law.

Appendices

Appendix A: Characteristic polynomials of the linearized ODE system

Here we give the coefficient $a_i$, $i=1,\ldots ,4$ for the characteristic polynomial of the linearized system in Theorem 1:

$$\begin{aligned} \displaystyle a_1&= \displaystyle \left( \mu +\gamma _u+\tau \frac{\lambda _p}{\tau ^*u_\infty +\gamma _p}+\alpha n^2 u_\infty ^{n-1}+\rho \frac{\alpha }{\mu }u_\infty ^n+\gamma _p+\tau u_\infty +\sigma +\delta \right) ,\\ \displaystyle a_2&= \displaystyle \left( \mu +\gamma _u+\alpha n^2u_\infty ^{n-1}+\rho \frac{\alpha }{\mu }u_\infty ^n\right) (\gamma _p+\tau u_\infty +\sigma +\delta )+\gamma _p\sigma +(\gamma _p+\tau u_\infty )\delta \\&+\mu \left( \gamma _u+\tau \frac{\lambda _p}{\tau ^*u_\infty +\gamma _p}+\alpha n^2u_\infty ^{n-1}+\rho \frac{\alpha }{\mu }u_\infty ^n\right) +\rho \alpha nu_\infty ^n+\tau (\gamma _p+\delta )\frac{\lambda _p}{\tau ^*u_\infty +\gamma _p},\\ \displaystyle a_3&= \displaystyle \left( \mu +\gamma _u+\alpha n^2 u_\infty ^{n-1}+\rho \frac{\alpha }{\mu } u_\infty ^n\right) (\gamma _p\sigma \!+\!(\gamma _p\!+\!\tau u_\infty )\delta )\!+\!(\gamma _p\delta \!+\!(\!\gamma _p+\delta )\mu )\tau \frac{\lambda _p}{\tau ^* u_\infty +\gamma _p}\\&+ \left\{ \mu \left( \gamma _u+\alpha n^2u_\infty ^{n-1}+\rho \frac{\alpha }{\mu }u_\infty ^n\right) +\rho \alpha nu_\infty ^n\right\} (\gamma _p+\tau u_\infty +\sigma +\delta ),\\ \displaystyle a_4&= \displaystyle \mu \gamma _p\delta \tau \frac{\lambda _p}{\tau ^*u_\infty +\gamma _p} +\left\{ \mu \left( \gamma _u+\alpha n^2u_\infty ^{n-1}+\rho \frac{\alpha }{\mu }u_\infty ^n\right) +\rho \alpha nu_\infty ^n\right\} (\gamma _p\sigma +(\gamma _p+\tau u_\infty )\delta ). \end{aligned}$$

Appendix B: Lyapunov functional

Here we detail a Lyapunov function $\varPhi$ which is the key ingredient to prove global stability of system (8–11) in Proposition 2. This function appears to be a bit tricky, but determining it rest upon the backward method described for instance Chapter 4, p. 120, in the book by Khalil (1996). It consists in investigate an expression of the derivative $\varPhi '$ and then going back to chose the parameters $\varPhi$ such as $\varPhi '$ is negative definite. After tedious calculus, a Liapunov function $\varPhi$ for system (8–11) is given by

$$\begin{aligned} \varPhi&= \frac{1}{2}\left( \frac{2\gamma _p}{\delta }\right) s_1\theta _1^2+\frac{1}{2}\left( 1+2\frac{\delta +\gamma _u+\rho (A_\infty +\theta _1)}{\sigma }\right) \theta _2^2+\frac{1}{2}\left( \frac{2\gamma _p}{\delta }\right) \theta _3^2\\&+\frac{1}{2}\left( \frac{\sigma }{\gamma _p}\right) \theta _4^2+ \left( \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu }\right) \theta _1\theta _2+\theta _1\theta _3\\&+\left( \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu }+1+\frac{\rho }{\tau }\right) \theta _1\theta _4+\theta _2\theta _3 +2\theta _2\theta _4+\left( \frac{2\gamma _p}{\delta }\right) \theta _3\theta _4, \end{aligned}$$

where $\theta _1=A-A_\infty$, $\theta _2=u-u_\infty$, $\theta _3=p-p_\infty$, $\theta _4=b-b_\infty$, with $s_1=\max (T_1,T_2)$ such that

$$\begin{aligned} T_1&= \frac{\rho ^2\delta u_\infty ^2\left( 1+2\frac{1+\delta }{\sigma }\right) }{8\mu \gamma _p}+\frac{(\gamma _p+\mu )^2\left( \frac{\delta }{2\gamma _p}\right) ^2}{4\gamma _p\mu }\\&+\frac{\left[ (\delta +\mu )\left( \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu }+1\right) +(\sigma +\delta +\mu )\frac{\rho }{\tau }+2\rho u_\infty \right] ^2}{8\mu \sigma }, \end{aligned}$$

and $T_2 = \varGamma \left( \frac{\delta }{2\gamma _p}\right) ^2 T_2'$ with

$$\begin{aligned} T_2'&= \left( \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu } \right) ^2 \left\{ \frac{2\sigma +\delta }{2\gamma _p} +\left( \frac{\delta }{2\gamma _p} \varGamma \right) ^{-1}\left( \frac{1}{1+2\frac{\delta +\gamma _u}{\sigma }}\right) \right\} \\&+ \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu } \left\{ 2+4\frac{\rho }{\tau }\frac{\delta +\gamma _u}{\sigma }\right\} + \frac{\delta }{2\gamma _p}\left\{ \frac{\rho }{\tau }\left( 2+\frac{\rho }{\tau }\right) +\frac{\sigma +2(\delta +\gamma _u)}{\gamma _p}\right\} \\&+\left( 1+2\frac{\delta +\gamma _u}{\sigma }\right) \left\{ \frac{\rho }{\tau }\left( 1+\frac{\rho }{\tau }\right) + \frac{\delta }{2\gamma _p}\frac{\sigma }{\gamma _p}-1\right\} \end{aligned}$$

and

$$\begin{aligned} \varGamma =\frac{1}{\left( 1+2\frac{\delta +\gamma _u}{\sigma }-\frac{\delta }{2\gamma _p}\right) \left( \frac{\delta }{2\gamma _p}\frac{\sigma }{\gamma _p}-1\right) }\cdot \end{aligned}$$

We remark that $T_1>0$ so that $s_1 >0$, and then we deduce that the Lyapunov function $\varPhi$ is positive when condition $\left( 1+2\frac{\delta +\gamma _u}{\sigma }\right) >\frac{\delta }{2\gamma _p}>\frac{\gamma _p}{\sigma }$ holds true. In such case, its derivative along the solutions of system (8–11) is given by

$$\begin{aligned} \varPhi '&= \displaystyle -\displaystyle \left( \mu s_1+\rho u\frac{\delta }{2\gamma _p}\cdot \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu }\right) \theta _1^2-\rho u_\infty \frac{\delta }{2\gamma _p}\left( 1+2\frac{\gamma _u\!+\!\rho (A_\infty +\theta _1)\!+\!\delta }{\sigma }\right) \theta _1\theta _2 \\&- \displaystyle \frac{\delta }{2\gamma _p}\left( \frac{2(\gamma _u+\rho (A_\infty +\theta _1)+\tau p)(\gamma _u+\rho (A_\infty +\theta _1)+\delta )}{\sigma }+\gamma _u+\rho (A_\infty +\theta _1)\right) \theta _2^2 \\&- \displaystyle \frac{\delta }{2\gamma _p}\left( (\delta +\mu )\left( \frac{\rho p_\infty }{\gamma _u+\rho A_\infty +\mu }+1\right) +(\sigma +\delta +\mu )\frac{\rho }{\tau }+2\rho u_\infty \right) \theta _1\theta _4\\&- \displaystyle \left( \frac{\delta \tau u}{2\gamma _p}+\gamma _p\right) \theta _3^2-\delta \left( \frac{\sigma }{\gamma _p}\frac{\delta }{2\gamma _p}\right) \theta _4^2 - \frac{\delta }{2\gamma _p}(\gamma _p+\mu )\theta _1\theta _3. \end{aligned}$$

and remains nonpositive. Furthermore, $\varPhi '=0$ if and only if $\theta _1=\theta _2=\theta _3=\theta _4=0$. The conclusion holds by the LaSalle Invariance Principle LaSalle (1976).