Equilibria and stability of a class of positive feedback loops

Abstract

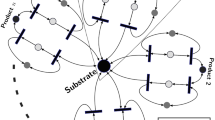
Positive feedback loops are common regulatory elements in metabolic and protein signalling pathways. The length of such feedback loops determines stability and sensitivity to network perturbations. Here we provide a mathematical analysis of arbitrary length positive feedback loops with protein production and degradation. These loops serve as an abstraction of typical regulation patterns in protein signalling pathways. We first perform a steady state analysis and, independently of the chain length, identify exactly two steady states that represent either biological activity or inactivity. We thereby provide two formulas for the steady state protein concentrations as a function of feedback length, strength of feedback, as well as protein production and degradation rates. Using a control theory approach, analysing the frequency response of the linearisation of the system and exploiting the Small Gain Theorem, we provide conditions for local stability for both steady states. Our results demonstrate that, under some parameter relationships, once a biological meaningful on steady state arises, it is stable, while the off steady state, where all proteins are inactive, becomes unstable. We apply our results to a three-tier feedback of caspase activation in apoptosis and demonstrate how an intermediary protein in such a loop may be used as a signal amplifier within the cascade. Our results provide a rigorous mathematical analysis of positive feedback chains of arbitrary length, thereby relating pathway structure and stability.

Appendix

In this section, we present three proofs required in Section 6, to prove the local stability of the off and on steady state.

1.1 A1: Proof of Lemma 1

Proof

From $h^i(s)$ in (54), we note that the roots of its characteristic polynomial are all negative if

$$\begin{aligned} {\mu ^{{i}}}>0. \end{aligned}$$

(72)

In the following, we show that ${\mu ^{{i}}}$ is positive for both steady states and for all $i$.

• 1. Off Steady State Considering the definition of the off steady state in (35a) and the definition of ${\sigma ^{{i}}}$ and ${\mu ^{{i}}}$, (72) becomes

  $$\begin{aligned} {\mu ^{{i}}}_{\mathrm{off}} ={k_{3f}^{{i}}}>0. \end{aligned}$$

• 2. On Steady State The on steady state is given by (35b), which is parametrised by ${\vartheta ^{{i+1}}}$ defined in (36). We note that (39b) allows us to express ${\mu ^{{i}}}_{\mathrm{on}}$ in (50) as

  $$\begin{aligned} {\mu ^{{i}}}_{\mathrm{on}} = {k_{1}^{{i}}} {{\bar{c}}^{{i+1}}_{2}} + {k_{3f}^{{i}}}&= \frac{{k_{2}^{{i+1}}}{k_{3f}^{{i}}} {\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} -{k_{1}^{{i}}}{\mathrm{n}\left( {\vartheta ^{{i+1}}} \right)}}{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}. \end{aligned}$$

  (73)

  Furthermore, we claim

  $$\begin{aligned} {k_{2}^{{i+1}}}{k_{3f}^{{i}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} = {\mathrm{d}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)} + {k_{1}^{{i}}} {\mathrm{n}\left( {\vartheta ^{{i+1}}} \right)}. \end{aligned}$$

  (74)

  We provide a proof of this statement in Claim 1, below. Hence ${\mu ^{{i}}}$ in (73) becomes

  $$\begin{aligned} {\mu ^{{i}}}_{\mathrm{on}} = \frac{{\mathrm{d}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}} >0 \quad \forall \quad i \in [1,{p}]. \end{aligned}$$

  (75)

$\square$

Now, we present the proof of (74).

Claim 1

For all $i \in [1,p]$

$$\begin{aligned} {k_{2}^{{i+1}}} {k_{3f}^{{i}}} {\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} = {\mathrm{d}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)} + {k_{1}^{{i}}} {\mathrm{n}\left( {\vartheta ^{{i+1}}} \right)}, \end{aligned}$$

where ${\alpha ^{{i}}}$ has been defined in (41a).

Proof

The strategy of the proof is to rewrite ${\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}$ in terms of ${\mathrm{d}\left( {\vartheta ^{{i}}} \right)}$. From (36), we have

$$\begin{aligned} {\mathrm{n}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}&= {\mathrm{n}\left( {\alpha ^{{i}}} \right)}\prod _{j=1}^{i}{\mathrm{d}\left( {\alpha ^{{j}}} \right)} \sum _{{\ell }=i+1}^{{p}}\left({k_{1}^{{ {\ell }}}} \prod _ {j=i+1}^{{\ell }-1}{\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{{p}}{\mathrm{d}\left( {\alpha ^{{j}}} \right)} \right)\\&+ \,{\mathrm{n}\left( {\alpha ^{{i}}} \right)}\prod _{j=i+1}^{{p}} {\mathrm{n}\left( {\alpha ^{{j}}} \right)}\sum _{{\ell }=1}^{i}\left({k_{1}^{{{\ell }}}}\prod _{ j=1}^{{\ell }-1}{\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{i}{\mathrm{d}\left( {\alpha ^{{j}}} \right)}\right)\\&= \prod _{j=1}^{i}{\mathrm{d}\left( {\alpha ^{{j}}} \right)} \sum _{{\ell }=i+1}^{{p}}\left({k_{1}^{{{\ell }}}}\prod _{j=i}^{{\ell }-1} {\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{{p}}{\mathrm{d}\left( {\alpha ^{{j}}} \right)}\right) \\&+ \prod _{j=i}^{{p}}{\mathrm{n}\left( {\alpha ^{{j}}} \right)}\sum _{{\ell }=1}^{i} \left({k_{1}^{{{\ell }}}}\prod _{j=1}^{{\ell }-1}{\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{i}{\mathrm{d}\left( {\alpha ^{{j}}} \right)}\right)\\&= {\mathrm{d}\left( {\alpha ^{{i}}} \right)} \left[ \prod _{j=1}^{i-1}{\mathrm{d}\left( {\alpha ^{{j}}} \right)} \sum _{k=i}^{{p}}\left({k_{1}^{{{\ell }}}}\prod _{j=i}^{{\ell }-1} {\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{{p}}{\mathrm{d}\left( {\alpha ^{{j}}} \right)}\right) \right. \\&+ \left.\prod _{j=i}^{{p}}{\mathrm{n}\left( {\alpha ^{{j}}} \right)}\sum _{{\ell }=1}^{i-1} \left({k_{1}^{{{\ell }}}} \prod _{j=1}^{ {\ell }-1 } {\mathrm{n}\left( {\alpha ^{{j}}} \right)}\prod _{j={\ell }+1}^{i-1}{\mathrm{d}\left( {\alpha ^{{j}}} \right)}\right) \right]\\&+\, {k_{1}^{{i}}} \left[ \prod _{j=1}^{{p}}{\mathrm{n}\left( {\alpha ^{{j}}} \right)} - \prod _{j=1}^{{p}}{\mathrm{d}\left( {\alpha ^{{j}}} \right)} \right] \\&= {\mathrm{d}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)} + {k_{1}^{{i}}}{\mathrm{n}\left( {\vartheta ^{{i+1}}} \right)}. \end{aligned}$$

$\square$

1.2 A2: Proof of Corollary 1

Proof

The closed-form expressions of $\det \left( {\mathbf{A}^{{} {}}}_{\mathrm{off}} \right)$ and $\det \left( {\mathbf{A}^{{} {}}}_{\mathrm{on}} \right)$ in (63a) and (63c), respectively, are derived in Lemma 4 in Sect. 8.

• 1. Off Steady State The off steady state is given in (35a). We note that when we evaluate the conditions (55b) at the off steady state (35a), we obtain

  $$\begin{aligned} {k_{2}^{{i}}} > {k_{3f}^{{i}}}, \quad {k_{3f}^{{i}}} \ge {k_{3f}^{{i}}}, \quad and \quad \frac{1}{\left( {k_{3f}^{{i}}} \right)^2} < \frac{1}{\left( {k_{2}^{{i}}} \right)^2} + \frac{1}{\left({k_{3f}^{{i}}}\right)^2}. \end{aligned}$$

  The later two expressions are always satisfied, given the parameters are positive. Now, the former condition ${k_{2}^{{i}}} > {k_{3f}^{{i}}}$ combined with the condition ${k_{2}^{{i}}} < {k_{3f}^{{i}}}$ in (55a), shows that we can guarantee the local stability of the off steady state for all parameter values that satisfy (56). Substituting (35a) into (56) yields

  $$\begin{aligned} \gamma _{\mathrm{off}} := \prod _{i=1}^{p}\frac{{k_{1}^{{i}}} {k_{3b}^{{i}}}}{{k_{2}^{{i}}} {k_{3f}^{{i}}}} < 1, \end{aligned}$$

  (76)

  or equivalently

  $$\begin{aligned} \prod _{i=1}^{p}{k_{2}^{{i}}} {k_{3f}^{{i}}} - \prod _{i=1}^{p}{k_{1}^{{i}}} {k_{3b}^{{i}}} > 0, \end{aligned}$$

  (63a)

  as stated in (63a).

• 2. On Steady State The on steady state is given by (35b), which is parametrised by ${\vartheta ^{{i+1}}}$ defined in (36). Moreover, we recall that

  $$\begin{aligned} {\mu ^{{i}}}_{\mathrm{on}} = \frac{{\mathrm{d}\left( {\alpha ^{{i}}} \right)} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}. \end{aligned}$$

  (75)

  In addition, we note that, with the expressions (38a) and (39b), ${\sigma ^{{i}}}$ in (50) may be rewritten as

  $$\begin{aligned} {\sigma ^{{i}}}_{\mathrm{on}} = {k_{1}^{{i}}}{{\bar{c}}^{{i}}_{1}} = \frac{{k_{2}^{{i+1}}} {\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} }{{\mathrm{d}\left( {\vartheta ^{{i}}} \right)} }. \end{aligned}$$

  With the two former expressions, the stability condition (56) becomes

  $$\begin{aligned} \gamma _{\mathrm{on}}:=\prod _{i=1}^{p}\gamma ^i_{\mathrm{on}} = \prod _{i=1}^{p}\frac{{k_{2}^{{i+1}}}}{{k_{2}^{{i}}}} \left( \frac{{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}{{\mathrm{d}\left( {\vartheta ^{{i}}} \right)}} \right)^2 \frac{{k_{2}^{{i+1}}}{k_{3f}^{{i}}}}{{k_{1}^{{i}}}{k_{3b}^{{i}}}}<1. \end{aligned}$$

  (77)

  Consequently, the small gain stability condition in (56) is

  $$\begin{aligned} \prod _{i=1}^{p}{k_{1}^{{i}}} {k_{3b}^{{i}}} - \prod _{i=1}^{p}{k_{2}^{{i}}}{k_{3f}^{{i}}}&>0, \end{aligned}$$

  (63c)

  where we have taken into account the modularity of the superindex $i$ in ${k_{2}^{{i+1}}}$.

$\square$

1.3 A3: Closed form of the determinant of ${\mathbf{A}^{{} {}}}_{\mathrm{off}}$ and ${\mathbf{A}^{{} {}}}_{\mathrm{on}}$

In order to prove the closed-form expression of the determinant of (47) in Theorem 4, we will exploit the following lemma that presents a formula for the determinant of a block matrix.

Lemma 2

Let a square matrix $\mathbf M$ be defined by blocks:

$$\begin{aligned} \mathbf{M} = \begin{pmatrix} \mathbf{M^{11}}&\mathbf{M^{12}}\\ \mathbf{M^{21}}&\mathbf{M^{22}} \end{pmatrix}, \end{aligned}$$

Provided the existence of $\left(\mathbf{M^{22}}\right)^{-1}$, the determinant of $\mathbf{M}$ is given by

$$\begin{aligned} \det \left( \mathbf{M} \right) = \det \left( \mathbf{M^{22}}\right) \det \left(\mathbf{M^{11}} - \frac{1}{\det \left(\mathbf{M^{22}}\right)}\mathbf{M^{12}}\mathrm{Adj}^T\left(\mathbf{M^{22}}\right)\mathbf{M^{21}} \right), \end{aligned}$$

where $\mathrm{Adj}^T\left(\mathbf{X}\right)$ denotes the transpose of the Adjugate or Adjoint matrix of $\,\mathbf{X}$.

We will also avail of the following theorem, which shows how to compute the determinant of a sum of matrices.

Lemma 3

(Matrix Determinant Lemma) Let $\mathbf{A}$ be a non-singular square matrix and $\mathbf{x, y}$ be column vectors of the dimension of $\mathbf{A}$, then

$$\begin{aligned} \det \left( \mathbf{A + x y^T} \right) = \det (\mathbf{A}) + \mathbf{y^T}\text{ Adj}^T\left(\mathbf{A}\right) \mathbf{x}. \end{aligned}$$

The proof of the previous lemmas can be found in Bernstein (2009), for example. Now, we use these theorems to prove the forthcoming lemma.

Lemma 4

The determinant of (47) is given by

• 1. Off Steady State

  $$\begin{aligned} \det \left( \mathbf{A_{\mathrm{off}}} \right) = \prod _{i=1}^{p}{k_{2}^{{i}}} {k_{3f}^{{i}}} - \prod _{i=1}^{p}{k_{1}^{{i}}} {k_{3b}^{{i}}} \end{aligned}$$

• 2. On Steady State

  $$\begin{aligned} \det \left(\mathbf{A_{\mathrm{on}}} \right) = \prod _{i=1}^{p}{k_{1}^{{i}}} {k_{3b}^{{i}}} - \prod _{i=1}^{p}{k_{2}^{{i}}} {k_{3f}^{{i}}} \end{aligned}$$

Proof

The strategy of the proof follows a recursive application of the Lemma 2, finalised by the application of Lemma 3 to obtain a closed-form expression for the determinant. We note that applying ${p}-1$ times Lemma 2, the determinant of (47) can be expressed as

$$\begin{aligned} \det \left(\mathbf{A}\right)&= \prod _{i = 2}^{p}\det \left( {\mathbf{A}^{{i} {i}}} \right)\det \left( {\mathbf{A}^{{1} {1}}} - \prod _{i=2}^{{p}} \frac{1}{\det \left( {\mathbf{A}^{{i} {i}}}\right)} \left[\prod _{i=1}^{{p}-1} -\mathbf A^{i,i+1} \mathrm{Adj}^T\left( \mathbf A^{i+1,i+1} \right)\right] {\mathbf{A}^{{{p}} {1}}} \right).\qquad \end{aligned}$$

(78)

Moreover, we note that

$$\begin{aligned} -{\mathbf{A}^{{{p}-1} {{p}}}} \mathrm{Adj}^T\left( {\mathbf{A}^{{{p}} {{p}}}} \right){\mathbf{A}^{{{p}} {1}}}&= -{\sigma ^{{{p}-1}}}\begin{pmatrix} 0&\quad -1\\ 0&\quad 1 \end{pmatrix} \begin{pmatrix} -{k_{2}^{{{p}}}}&\quad 0\\ {k_{1}^{{{p}}}} {{\bar{c}}^{{1}}_{2}}&\quad -{\mu ^{{{p}}}} \end{pmatrix}{\sigma ^{{{p}}}} \begin{pmatrix} 0&\quad -1\\ 0&\quad 1 \end{pmatrix}\\&= {k_{3f}^{{{p}}}} {\sigma ^{{{p}-1}}}{\sigma ^{{{p}}}} \begin{pmatrix} 0&\quad -1\\ 0&\quad 1 \end{pmatrix}. \end{aligned}$$

where ${\sigma ^{{i}}}$ and ${\mu ^{{i}}}$ have been defined in (50). Hence

$$\begin{aligned} \left[\prod _{i=1}^{{p}-1} -\mathbf{A}^{i,i+1} \mathrm{Adj}^T\left( \mathbf{A}^{i+1,i+1} \right)\right] {\mathbf{A}^{{{p}} {1}}}&= {\sigma ^{{1}}}\left[\prod _{i=2}^{p}{k_{3f}^{{i}}} {\sigma ^{{i}}}\right] \begin{pmatrix} 0&\quad -1\\ 0&\quad 1 \end{pmatrix}. \end{aligned}$$

Substituting the expression above into (78), yields

$$\begin{aligned} \det \left(\mathbf{A}\right)&= \prod _{i = 2}^{p}\det \left( {\mathbf{A}^{{i} {i}}} \right)\det \left( {\mathbf{A}^{{1} {1}}} + {\sigma ^{{1}}} \prod _{i=2}^{{p}} \frac{1}{\det \left( {\mathbf{A}^{{i} {i}}}\right)} \left[\prod _{i=2}^{p}{k_{3f}^{{i}}} {\sigma ^{{i}}}\right] \begin{pmatrix} 0&\quad -1\\ 0&\quad 1 \end{pmatrix}\right). \end{aligned}$$

By Lemma 3 and ${\mathbf{A}^{{i} {i}}}$ in (49a), the expression above becomes

$$\begin{aligned} \det \left(\mathbf{A}\right)&= \prod _{i = 2}^{p}\det \left( {\mathbf{A}^{{i} {i}}} \right) \left[ \det \left({\mathbf{A}^{{1} {1}}}\right) - \prod _{i=2}^{{p}} \frac{1}{\det \left( {\mathbf{A}^{{i} {i}}}\right)} \prod _{i=1}^{p}{k_{3f}^{{i}}} {\sigma ^{{i}}}\right],\nonumber \\ \det \left(\mathbf{A}\right)&= \prod _{i = 1}^{p}{k_{2}^{{i}}}{\mu ^{{i}}} - \prod _{i=1}^p{k_{3f}^{{i}}} {\sigma ^{{i}}}. \end{aligned}$$

(79)

We further consider the definition of the steady states, to conclude the proof.

• 1. Off Steady State By substituting the definition of this equilibrium point in (35a), into (79), we obtain the expression

  $$\begin{aligned} \det \left(\mathbf{A_{\mathrm{off}}} \right)&= \prod _{i=1}^{p}{k_{2}^{{i}}} {k_{3f}^{{i}}} - \prod _{i=1}^{p}{k_{1}^{{i}}} {k_{3b}^{{i}}}, \end{aligned}$$

  as desired.

• 2. On Steady State This equilibrium point is parametrised by ${\vartheta ^{{i+1}}}$, defined in (36), via the relationships (39a) and (39b). Firstly, we analyse the product of the main blocks determinants in (79). By means of (39b) we can rewrite it as

  $$\begin{aligned} \det \left( {\mathbf{A}^{{i} {i}}}_{\mathrm{on}} \right)&= {k_{2}^{{i}}}\frac{{k_{3f}^{{i}}} {k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} - {k_{1}^{{i}}} {\mathrm{n}\left( {\vartheta ^{{i+1}}} \right)} }{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}\\ \det \left( {\mathbf{A}^{{i} {i}}}_{\mathrm{on}} \right)&= {\mathrm{d}\left( {\alpha ^{{i}}} \right)} \frac{{k_{2}^{{i}}} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}, \end{aligned}$$

  where we availed of the expression in (74). From the expression above, we note

  $$\begin{aligned} \prod _{i=1}^{p}\det \left( {\mathbf{A}^{{i} {i}}}_{\mathrm{on}} \right)&= \prod _{i=1}^{p}{\mathrm{d}\left( {\alpha ^{{i}}} \right)} \frac{{k_{2}^{{i}}} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}{{k_{2}^{{i+1}}}{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}\nonumber \\ \prod _{i=1}^{p}\det \left( {\mathbf{A}^{{i} {i}}}_{\mathrm{on}} \right)&= \prod _{i=1}^{p}{k_{1}^{{i}}}{k_{3b}^{{i}}} . \end{aligned}$$

  (80)

  Secondly, we note that, with the expressions (38a) and (39b), ${{\bar{c}}^{{i}}_{1}}$ may be rewritten as

  $$\begin{aligned} {{\bar{c}}^{{i}}_{1}} = \frac{{k_{2}^{{i+1}}} {\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)} }{{k_{1}^{{i}}} {\mathrm{d}\left( {\vartheta ^{{i}}} \right)} }. \end{aligned}$$

  Hence the later product in (79) becomes

  $$\begin{aligned} \prod _{i=1}^{p}{k_{3f}^{{i}}}{k_{1}^{{i}}}{{\bar{c}}^{{1}}_{i}} = \prod _{i=1}^{p}{k_{3f}^{{i}}}{k_{2}^{{i+1}}}. \end{aligned}$$

  Subtraction of (80) and the relationship above, yields

  $$\begin{aligned} \det \left( \mathbf{A}_{\mathrm{on}} \right) = \prod _{i=1}^{p}{k_{1}^{{i}}}{k_{3b}^{{i}}} - \prod _{i=1}^{p}{k_{3f}^{{i}}}{k_{2}^{{i}}}, \end{aligned}$$

  when exploiting the modularity of the product with respect to ${p}$.

$\square$

Now, we provide the proof of Theorem 5, which determines the stability of the on steady state under the conditions on the parameters described in (64).

1.4 A4: Proof of Theorem 5

Proof

Accounting for the conditions (64), the solution for $\varOmega ^*$ in (59) is positive and real, for the positive sign of the square root. Let us rewrite this solution as

$$\begin{aligned} \varOmega ^*&= - \left( {k_{3f}^{{i}}} \right)^2 + \sqrt{\left[ \left({k_{3f}^{{i}}}\right)^2 - \left({k_{2}^{{i}}}\right)^2 \right] \left[ \left({k_{3f}^{{i}}}\right)^2 - \left({\mu ^{{i}}}_{\mathrm{on}}\right)^2 \right]}=:- \left( {k_{3f}^{{i}}} \right)^2 + \phi ^i\eta ^i,\nonumber \\ \end{aligned}$$

(81)

where

$$\begin{aligned} \phi ^i&= \sqrt{\left( {k_{2}^{{i}}}\right)^2 -\left({k_{3f}^{{i}}}\right)^2},\end{aligned}$$

(82a)

$$\begin{aligned} \eta ^i&= \sqrt{\left( {\mu ^{{i}}}_{ on }\right)^2 -\left({k_{3f}^{{i}}}\right)^2}. \end{aligned}$$

(82b)

Then, from (58), the gain of the system evaluated in the peak frequency (81) is

$$\begin{aligned} \gamma _{ on }^i&= \sigma ^i\sqrt{\frac{\phi ^i\eta ^i}{\left[-\left({k_{3f}^{{i}}}\right)^2 + \phi ^i\eta ^i+ \left( {\mu ^{{i}}}_{\mathrm{on}} \right)^2 \right]\left[-\left({k_{3f}^{{i}}}\right)^2 + \phi ^i\eta ^i + \left( {k_{2}^{{i}}}\right)^2 \right]}}\nonumber \\&= \sigma ^i\sqrt{\frac{1}{\left( \phi ^i \right)^2 + 2\phi ^i\eta ^i + \left( \eta ^i \right)^2}}\nonumber \\&= \frac{\sigma ^i}{\phi ^i + \eta ^i}\nonumber \\&= \frac{\sigma ^i}{\sqrt{\left( {k_{2}^{{i}}}\right)^2 -\left({k_{3f}^{{i}}}\right)^2} + \sqrt{\left( {\mu ^{{i}}}_{ on }\right)^2- \left({k_{3f}^{{i}}}\right)^2}} \\&= \frac{\sigma ^i{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{\mathrm{on}}{k_{2}^{{i}}}} \frac{{k_{2}^{{i}}}}{{k_{3f}^{{i}}}} \frac{{\mu ^{{i}}}_{\mathrm{on}}}{\sqrt{\left({k_{2}^{{i}}}\right)^2 -\left({k_{3f}^{{i}}}\right)^2} + \sqrt{\left( {\mu ^{{i}}}_{\mathrm{on}}\right)^2-\left({k_{3f}^{{i}}}\right)^2}}\nonumber \\ \gamma _{\mathrm{on}}^i&= \frac{{k_{2}^{{i+1}}} {k_{3f}^{{i}}}}{{k_{1}^{{i}}}{k_{3b}^{{i}}}} \frac{{k_{2}^{{i+1}}}}{{k_{2}^{{i}}}} \left[\frac{{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}{{\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}\right]^2 \frac{1}{\frac{{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{\mathrm{on}}}\sqrt{1 -\left(\frac{{k_{3f}^{{i}}}}{{k_{2}^{{i}}}}\right)^2} + \frac{{k_{3f}^{{i}}}}{{k_{2}^{{i}}}}\sqrt{1-\left(\frac{{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{\mathrm{on}}} \right)^2}}. \nonumber \end{aligned}$$

(83)

In the derivation of the expression above, we exploited the definitions in (82) and (50). Except for the last factor, the expression above resembles the gain for the on steady state in (77), analysed in Theorem 4. Moreover, we have just considered that for some $i$, the conditions in (64) are satisfied. Then the stability condition form the Small Gain Theorem can be expressed as

$$\begin{aligned} \prod _{i=1}^{p}\frac{{k_{2}^{{i+1}}}{k_{3f}^{{i}}}}{{k_{1}^{{i}}} {k_{3b}^{{i}}}} \left( \theta ^i \right)^{-1}&< 1\\ \prod _{i=1}^{p}\frac{{k_{2}^{{i+1}}} {k_{3f}^{{i}}} }{{k_{1}^{{i}}} {k_{3b}^{{i}}}}&< \prod _{i=1}^{p}\theta ^i, \end{aligned}$$

where the definition of $\theta ^i$ is given in (66). Although exact, the condition above might be an intricate function of the parameters. In the following, we pursue a tractable bound of $\gamma _{\mathrm{on}}^i$. To this end we note that (64c) implies

$$\begin{aligned} 1 -\left(\frac{{k_{3f}^{{i}}}}{{k_{2}^{{i}}}}\right)^2&> \left(\frac{{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{ on } }\right)^2\\ 1 - \left(\frac{{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{ on } }\right)^2&> \left(\frac{{k_{3f}^{{i}}}}{{k_{2}^{{i}}}}\right)^2 \end{aligned}$$

Using these two last inequalities in (83), we obtain the bound

$$\begin{aligned} \gamma _\mathrm{{on}}^i&< \frac{\sigma ^i}{{k_{2}^{{i}}}\frac{{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{\mathrm{on}}} + {\mu ^{{i}}}_\mathrm{{on}}\frac{{k_{3f}^{{i}}}}{{k_{2}^{{i}}}}}\\&= \frac{{k_{2}^{{i}}}}{{k_{3f}^{{i}}}} \frac{\sigma ^i{\mu ^{{i}}}_{\mathrm{on}} }{ \left( {k_{2}^{{i}}} \right)^2 + \left( {\mu ^{{i}}}_\mathrm{{on}} \right)^2}\\&= \frac{\sigma ^i{k_{3f}^{{i}}}}{{\mu ^{{i}}}_{\mathrm{on}}{k_{2}^{{i}}}} \left( \frac{{k_{2}^{{i}}}}{{k_{3f}^{{i}}}} \right)^2 \frac{\left( {\mu ^{{i}}}_\mathrm{{on}} \right)^2 }{ \left( {k_{2}^{{i}}} \right)^2 + \left( {\mu ^{{i}}}_\mathrm{{on}} \right)^2} \\&= \frac{{k_{2}^{{i+1}}} {k_{3f}^{{i}}}}{{k_{1}^{{i}}}{k_{3b}^{{i}}}} \frac{{k_{2}^{{i+1}}}}{{k_{2}^{{i}}}} \left[\frac{{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}{{\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}\right]^2 \left( \frac{{k_{2}^{{i}}}}{{k_{3f}^{{i}}}}\right)^2 \frac{\left( {\mu ^{{i}}}_\mathrm{{on}} \right)^2 }{ \left( {k_{2}^{{i}}} \right)^2 + \left( {\mu ^{{i}}}_\mathrm{{on}} \right)^2}\\&< \frac{{k_{2}^{{i+1}}} {k_{3f}^{{i}}}}{{k_{1}^{{i}}}{k_{3b}^{{i}}}} \frac{{k_{2}^{{i+1}}}}{{k_{2}^{{i}}}} \left[\frac{{\mathrm{d}\left( {\vartheta ^{{i+1}}} \right)}}{{\mathrm{d}\left( {\vartheta ^{{i}}} \right)}}\right]^2 \left( \frac{{k_{2}^{{i}}}}{{k_{3f}^{{i}}}}\right)^2. \end{aligned}$$

Here we used the definitions of ${\mu ^{{i}}}_\mathrm{{on}}$ and ${\sigma ^{{i}}}$ in (50). Again, the expression above resembles the gain for the on steady state in (77), analysed in Theorem 4. Since the conditions in (64) just hold for some $i$, the stability of the closed loop is guaranteed if (67) holds. $\square$