Extending the type reproduction number to infectious disease control targeting contacts between types

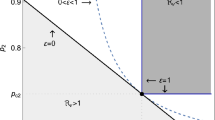
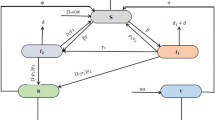
Abstract

A new quantity called the target reproduction number is defined to measure control strategies for infectious diseases with multiple host types such as waterborne, vector-borne and zoonotic diseases. The target reproduction number includes as a special case and extends the type reproduction number to allow disease control targeting contacts between types. Relationships among the basic, type and target reproduction numbers are established. Examples of infectious disease models from the literature are given to illustrate the use of the target reproduction number.

Appendix

 

Proof of Theorem 2.1

Observe that $I-(K-P_{S_1}KP_{S_2})$ is a nonsingular $M$-matrix since $K-P_{S_1}KP_{S_2}$ is nonnegative with spectral radius less than 1. For definition and properties of $M$-matrices, see Berman and Plemmons (1979). It follows that $M:= P_{S_1} K P_{S_2} (I-K+P_{S_1} K P_{S_2})^{-1}$ is nonnegative, and $(I-M)P_{S_1}KP_{S_2}=M(I-K)$. Since $S_1$ includes all indices of rows where $M$ has nonzero entries, it follows that $\rho (M)=\rho (E_{S_1}ME_{S_1})=\mathcal T _{S}$. Let $w$ be a positive eigenvector of the nonnegative irreducible matrix $K$ with respect to $\rho (K)=\mathcal R _0$. Then

$$\begin{aligned} (I-M)P_{S_1}KP_{S_2}w=M(I-K)w=(1-\mathcal R _0)Mw. \end{aligned}$$

(6.1)

Notice that all indices of nonzero rows of $M$ are included in $S_1$. Also notice that $P_{S_1}KP_{S_2}w$ is a vector in $\mathbb R ^n$ with positive entries only in each position $j \in S_1$. If $\mathcal R _0=\rho (K)<1$, then $(1-\mathcal R _0)Mw>0$, thus (6.1) gives $MP_{S_1}KP_{S_2}w<P_{S_1}KP_{S_2}w$. By applying a result of Collatz to the rows whose indices are included in $S_1$ (see, for example, (Horn and Johnson 1985, Corollary 8.1.29)), $\mathcal T _S=\rho (M)<1$. If $\mathcal T _S<1$, then $\mathcal R _0<1$ from (6.1). Similarly, it can be shown that $\mathcal R _0=1$ iff $\mathcal T _S=1$, and $\mathcal R _0>1$ iff $\mathcal T _S>1$. $\square$

 

Proof of Theorem 2.2

Since each targeted entry of $K$ appears only in the term $P_{S_1}KP_{S_2}$ in (2.1), $\mathcal T _S$ depends linearly on the targeted entry. Let $\mathcal T _{S}^c$ be the target reproduction number corresponding to $K_c$, thus $\mathcal T _{S}^c =\mathcal T _{S}/\mathcal T _{S}=1$, which implies $\rho (K_c)=1$, by Theorem 2.1. $\square$

 

Proof of Theorem 4.2

Consider the next-generation matrix $K^T$, the transpose of $K$, and let ${\hat{\mathcal{T }}_S}$ be the corresponding target reproduction number with respect to the target $S$ (i.e., $K$ in (2.1) is replaced by $K^T$). Let ${\hat{K}_{c}}$ be the controlled next-generation matrix corresponding to $K^T$ and target set $S$, defined as in Theorem 2.2; that is, the $(i,j)$ entry $k_{ji}$ in $K^T$ is replaced by $k_{ji}/{\hat{\mathcal{T }}}_S$ if $(i,j)\in S$. Similarly, let $K_{\hat{c}}$ be the controlled next-generation matrix corresponding to $K$ and target set $S^T$; that is, the $(j,i)$ entry $k_{ji}$ in $K$ is replaced by $k_{ji}/\mathcal T _{S^T}$ if $(i,j) \in S$. Notice that if $\mathcal T _{S^T}={\hat{\mathcal{T }}}_S$, then ${\hat{K}_c}=(K_{\hat{c}})^T$ and $\rho ({\hat{K}_c})=\rho (K_{\hat{c}})$. Now suppose that $\mathcal T _{S^T}\not ={\hat{\mathcal{T }}}_S$, then either $k_{ji}/{\hat{\mathcal{T }}}_S>k_{ji}/\mathcal T _{S^T}$ for all $(i,j)\in S$, or $k_{ji}/{\hat{\mathcal{T }}}_S<k_{ji}/\mathcal T _{S^T}$ for all $(i,j)\in S$. By the monotone property of the spectral radius of nonnegative irreducible matrices (e.g., see (Berman and Plemmons 1979, p. 27)), $\rho (K_{\hat{c}}) \not =\rho ({\hat{K}_c})$, contradicting $\rho (K_{\hat{c}}) =\rho ({\hat{K}_c})=1$ required by Theorem 2.2. Hence, $\mathcal T _{S^T}={\hat{\mathcal{T }}_S}$.

On the other hand, since $K$ is irreducible and the associated weighted digraph $\mathcal G$ is weight balanced, there exists a nonsingular $n\times n$ diagonal matrix $D$ such that $M=DKD^{-1}$ is symmetric; see, for example, Corollary 1 in Kolotilina (1993). It follows that $DKD^{-1}=M=M^T=(DKD^{-1})^T=D^{-1}K^T D$, and thus $K^T=D^2 K (D^{-1})^2$. Hence

$$\begin{aligned} {\hat{\mathcal{T }}_S}&= \rho (P_{S_1} K^T P_{S_2} (I-K^T+P_{S_1} K^T P_{S_2})^{-1})\\&= \rho (P_{S_1} D^2 K (D^{-1})^2 P_{S_2} (I-D^2 K (D^{-1})^2+P_{S_1} D^2 K (D^{-1})^2 P_{S_2})^{-1})\\&= \rho (D^2 P_{S_1} K (D^{-1})^2 P_{S_2} D^2 (I- K +P_{S_1}K P_{S_2})^{-1}(D^{-1})^2)\\&= \rho (D^2 P_{S_1} K P_{S_2}(I- K +P_{S_1}K P_{S_2})^{-1}(D^2)^{-1})\\&= \rho (P_{S_1} K P_{S_2}(I- K +P_{S_1}K P_{S_2})^{-1})\\&= \mathcal T _{S}. \end{aligned}$$

Therefore, $\mathcal T _S=\mathcal T _{S^T}$. $\square$

 

Proof of Theorem 4.3

It follows from Theorem 2.1 that $\mathcal T _S = \mathcal T _U =1$ if and only if $\mathcal R _0=1$, and that $\mathcal T _S>1$ and $\mathcal T _U>1$ if $\mathcal R _0>1$. The relation between $\mathcal T _S$ and $\mathcal T _U$ for $\mathcal R _0>1$ is proved by contradiction. Suppose that $\mathcal T _U>\mathcal T _S$. Let $K_{c_S}$ and $K_{c_U}$ be the controlled next-generation matrices defined as in Theorem 2.2, that is, the entry $k_{ij}$ in the next-generation matrix $K$ is replaced by $k_{ij}/\mathcal T _S$ (or $k_{ij}/\mathcal T _U$) if $(i,j)\in S$ (or $(i,j)\in U$). Since $\mathcal T _U>\mathcal T _S>1$ and $S\subset U$, it follows that $K_{c_S} > K_{c_U}$. Hence, by the monotone property of the spectral radius of nonnegative irreducible matrices (e.g., see (Berman and Plemmons 1979, p. 27)), $\rho (K_{c_S}) > \rho (K_{c_U})$, contradicting $\rho (K_{c_S}) = \rho (K_{c_U})=1$ required by Theorem 2.2. Therefore, $\mathcal T _S > \mathcal T _U >1$ if $\mathcal R _0>1$. A similar argument can be used to show that $\mathcal T _S < \mathcal T _U < 1$ if $\mathcal R _0<1$. $\square$