Mathematical modelling of competitive LDL/VLDL binding and uptake by hepatocytes

Abstract

Elevated levels of low-density-lipoprotein cholesterol (LDL-C) in the plasma are a well-established risk factor for the development of coronary heart disease. Plasma LDL-C levels are in part determined by the rate at which LDL particles are removed from the bloodstream by hepatic uptake. The uptake of LDL by mammalian liver cells occurs mainly via receptor-mediated endocytosis, a process which entails the binding of these particles to specific receptors in specialised areas of the cell surface, the subsequent internalization of the receptor–lipoprotein complex, and ultimately the degradation and release of the ingested lipoproteins’ constituent parts. We formulate a mathematical model to study the binding and internalization (endocytosis) of LDL and VLDL particles by hepatocytes in culture. The system of ordinary differential equations, which includes a cholesterol-dependent pit production term representing feedback regulation of surface receptors in response to intracellular cholesterol levels, is analysed using numerical simulations and steady-state analysis. Our numerical results show good agreement with in vitro experimental data describing LDL uptake by cultured hepatocytes following delivery of a single bolus of lipoprotein. Our model is adapted in order to reflect the in vivo situation, in which lipoproteins are continuously delivered to the hepatocyte. In this case, our model suggests that the competition between the LDL and VLDL particles for binding to the pits on the cell surface affects the intracellular cholesterol concentration. In particular, we predict that when there is continuous delivery of low levels of lipoproteins to the cell surface, more VLDL than LDL occupies the pit, since VLDL are better competitors for receptor binding. VLDL have a cholesterol content comparable to LDL particles; however, due to the larger size of VLDL, one pit-bound VLDL particle blocks binding of several LDLs, and there is a resultant drop in the intracellular cholesterol level. When there is continuous delivery of lipoprotein at high levels to the hepatocytes, VLDL particles still out-compete LDL particles for receptor binding, and consequently more VLDL than LDL particles occupy the pit. Although the maximum intracellular cholesterol level is similar for high and low levels of lipoprotein delivery, the maximum is reached more rapidly when the lipoprotein delivery rates are high. The implications of these results for the design of in vitro experiments is discussed.

1 1 Introduction

In this paper, we explore the hypothesis that another lipoprotein particle, namely very low density lipoprotein (VLDL), may interfere with hepatic uptake of low density lipoprotein (LDL), and that raised levels of VLDL in the circulation may be one mechanism by which low-density-lipoprotein cholesterol (LDL-C) levels can become elevated. All animal cells require cholesterol for the synthesis of cell membranes; however, too much cholesterol is cytotoxic. Mammalian organisms have evolved complex mechanisms to ensure that excessive cellular accumulation of cholesterol is avoided. Cholesterol is transported through the bloodstream to major organs by a family of macromolecular complexes called lipoproteins [2,13]. In humans, the majority of plasma cholesterol is found within low density lipoproteins (LDL). An elevated level of plasma LDL-cholesterol (LDL-C) is widely accepted as a high risk factor for the development of cardiovascular disease (CVD). LDL-C levels are in part determined by the rate at which they are taken up by hepatocytes; this highly controlled process, which we now summarise, is known as receptor-mediated endocytosis, and was elucidated in a series of classical experiments by Brown and Goldstein [4]. The first step is the binding of an LDL particle to specific hepatic LDL receptors (LDLR), in specialised regions of the liver cell surface, known as clathrin-coated pits. The LDL particle-receptor interaction is mediated by apolipoprotein B-100 (apoB-100) present on the surface of LDL particles. Upon binding to the LDLR, LDL particles are internalised into the cell, forming intracellular vesicles known as endosomes. Fusion of endosomes with lysosomes results in the degradation of the LDL particles, and the release of their constituent parts (cholesterol, fatty acids and amino acids). The LDLRs are either recycled to the cell surface, prior to lysosomal fusion, or degraded.

In vitro experiments of Jackson et al. [11] have shown that the rate of LDL endocytosis is influenced by the presence of other plasma lipoproteins, namely the very low density lipoproteins (VLDL). VLDL particles bind to the LDLR via apolipoprotein E (apoE)molecules, thus competingwith LDL for binding to the LDLR. VLDL particles isolated from individuals following consumption of single meals enriched in different dietary fatty acids have been shown to compete with varying effectiveness with LDL for hepatic uptake, an effect which is attributed to the variation in apoE content. VLDL particles isolated following a saturated fat (SAFA)-rich meal were shown to reduce the uptake of LDL by hepatocytes to a greater extent when compared with VLDL particles isolated following polyunsaturated (PUFA) and monounsaturated fatty acid (MUFA)-rich meals (see Fig. 1 for details). VLDL isolated following a PUFA-rich meal and those isolated following a MUFA-rich meal carry an average of two molecules of apoE per particle (and hence we refer to them as VLDL-2), whereas VLDL particles isolated following a meal rich in SAFA carry an average of three apoE molecules per particle (and hence are referred to as VLDL-3). Understanding the impact of the interplay between VLDL and LDL on cellular cholesterol homeostasis is of importance in understanding the mechanisms by which diet influences plasma LDL-C levels, and hence, in the longer term, CVD risk.

Fig. 1

Experimental results of Jackson et al. [11] showing how increasing VLDL levels inhibit LDL uptake by Hep-G2 cells

In this paper we formulate and study a mathematical model for hepatic uptake of LDL particles and both types of VLDL particles. The model is developed in Sect. 2 and accounts for the key processes involved during endocytosis of LDL, VLDL-2 and VLDL-3 particles. In earlier work [14,16], we have developed a model of the endocytosis of LDL particles bound to receptors which are clustered in pits. We assume that internalisation occurs by the pit invaginating into the cell, with the cell surface from the pit becoming the membrane lining of the endosome. Each endosome thus corresponds to an internalised pit. Cholesterol from the LDL and VLDL particles is then taken into the cell. A fraction of pits are recycled to the cell surface and, in addition, new pits are formed at a rate which is dependent on the cell's internal cholesterol level. Hence both the number of external pits, and the total number of pits and endosomes, are both variable.

This model has been parameterised against the experimental data of Brown and Goldstein, and generalised to include continuous delivery of LDL to the cells. In Panovska et al. [14] and Tindall et al. [15] we formulate a different type of model in which we consider a distribution of receptors; some on the surface of the hepatocyte, and the remainder internalised. Those on the surface are divided into two categories: the ‘bound’ which have an LDL or VLDL already bound to them, and the ‘free’, which have no LDL or VLDL bound to them. This model is used to investigate the competition between LDL and both types of VLDL particles for receptors, but ignores the fact that receptors are clustered into pits, in which many receptors are simultaneously internalised. In this paper we generalise the former model presented in [16] to allow for the competition between LDL and VLDL in the extracellular space for receptors in pits.

The model is used to study an in vitro experimental system in which a fixed amount of lipoprotein is delivered to the hepatocytes, as in the in vitro experimental systems of Brown and Goldstein [4], and Jackson et al. [11]. We aim to reproduce the experimental results of [11] in which VLDL inhibits LDL uptake. The model is then modified to consider a situation which better represents the in vivo scenario where the liver is typically exposed to a continuous supply of lipoprotein (for example, following a meal containing fat). In Sect. 2.4 we nondimensionalise the model equations and estimate the model parameters using data from the available literature. Section 3 contains our numerical results, a comparison with experimental results, and predictions of in vivo behaviour based on the modified system. To confirm the numerical results, we perform a steady state analysis in Sect. 4 where we also explore the long term behaviour of the system. A discussion of our key results is contained in Sect. 5.

2 2 Mathematical model of lipoprotein endocytosis

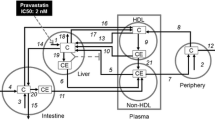
In this section we formulate a mathematical model for the dynamics of LDL endocytosis in the presence of VLDL-2 and VLDL-3. We account for the reversible binding and irreversible internalisation of LDL, VLDL-2 and VLDL-3, together with the subsequent release of cholesterol within the cell. The flows of material into and around the cell are illustrated in Fig. 2.

Fig. 2

An illustration of the processes considered in the uptake of LDL and VLDL particles by a single hepatocyte cell

The equations are constructed in two stages: firstly we build a detailed model in which each possible combination of p LDL particles, q VLDL-2 and r VLDL-3 particles are attached to a coated pit on the surface of the hepatocyte (p, q, r being integers upto ∼100). This framework represents ‘the microscopic model’ and consists of a large (∼10⁵) system of coupled ordinary differential equations.

By carefully specifying how the binding and unbinding rate parameters depend on the occupancy of the pit, it is possible to reduce the model to a system of just thirteen coupled ordinary differential equations. We refer to this reduced model as the ‘macroscopic model’. This remarkable simplification allows us to classify the coated pits as either occupied (by some combination of LDL, VLDL-2 and VLDL-3 particles), vacant, or internalised. The other ten variables are concentrations, one for the cell's internal cholesterol level, and three for LDL, VLDL-2 and VLDL-3 in each of three regions: extracellular, bound to the cell surface, or intracellular.

2.1 2.1 The microscopic model

We assume that LDL and VLDL-2/VLDL-3 endocytosis occurs in the following way: firstly extracellular LDL, VLDL-2 or VLDL-3 particles bind reversibly to receptors within the pits on the surface of a hepatocyte. When a pit is internalised all particles bound in the pit are internalised, and then broken down. Internalised lipoprotein particles release cholesterol which has several possible metabolic fates.

We denote the extracellular concentrations of LDL, VLDL-2 and VLDL-3 by $\bar L_e$ , $\bar V_{2e}$ and $\bar V_{3e}$ respectively, the concentration of bound LDL, VLDL-2 and VLDL-3 by $\bar L_i$ , $\bar V_{2i}$ and $\bar V_{3b}$, respectively, and the intracellular concentrations of LDL, VLDL-2 and VLDL-3 by $\bar L_i, \bar V_{2i}$ and $\bar V_{3i}$, respectively. We also denote the concentration of cholesterol released following lipoprotein endocytosis by $\bar C$ and the average number of receptors in a pit by r _m . We assume that an LDL particle covers only one receptor, and that VLDL-2 and VLDL-3 particles, due to their larger size, cover multiple receptors. We denote the number of receptors covered by VLDL-2 and VLDL-3 particles by Q and R, respectively. In summary we assume that lipoprotein endocytosis can be decomposed into the following sequence of reactions:

(2.1)

(2.2)

(2.3)

where $\bar k_L, \bar k_2, \bar k_3$ are the rates at which LDL, VLDL-2 and VLDL-3 are added to the external environment of the cell (delivery rates). The quantities $\bar a^+_{p,q,r}, \bar \alpha^+_{p,q,r}$ and $\bar \beta^+_{p,q,r}$ are the binding rates of LDL, VLDL-2 and VLDL-3 to receptors, and $\bar a^+_{p,q,r}, \bar \alpha^-_{p,q,r}$ and $\bar \beta^-_{p,q,r}$ are the respective unbinding rates. These depend on the occupancy of the pit, which is measured in terms of p, q, r, the numbers of LDL, VLDL-2, and VLDL-3 particles in the pit. These rates are defined for

$$\eqalign{ & \{ \bar a_{p.q,r}^ + :0 \le p + Qq + Rr < {r_m}\} ,{\rm{ }}\{ \bar a_{p.q,r}^ - :0 < p + Qq + Rr \le {r_m}\} , \cr & \{ \bar \alpha _{p.q,r}^ + :0 \le p + Qq + Rr < {r_m}\} ,{\rm{ }}\{ \bar \alpha _{p.q,r}^ - :0 < p + Qq + Rr \le {r_m}\} , \cr & \{ \bar \beta _{p.q,r}^ + :0 \le p + Qq + Rr < {r_m}\} {\rm{ and }}\{ \bar \beta _{p.q,r}^ - :0 < p + Qq + Rr \le {r_m}\} . \cr} $$

(2.4)

The quantity $\bar b$ is the pit internalisation rate. The rates of cholesterol production from internalised LDL, VLDL-2 and VLDL-3 are denoted by $\bar k_{ld}, \bar k_{2d}$ and $\bar k_{3d}$, respectively. The quantities $\bar \gamma, \bar \delta$ and $\bar \mu$ represent the number of cholesterol molecules in a typical LDL, VLDL-2 and VLDL-3 particle, respectively. The rate at which free cholesterol is esterified or removed from a cell is denoted by $\bar \gamma$.

Our model describes two different scenarios depending on how the rates $\bar k_L, \bar k_2$ and $\bar k_3$ are specified. We first consider the single-bolus case which models the experimental system of Jackson et al. [11] in which hepatocytes are exposed to a single dose of lipoprotein, (prior to the start of the experiment, hepatocytes have been deprived of lipoprotein). Initial conditions for $\bar L_e, \bar V_{2e}, \bar V_{3e}$ model a single dose (bolus) of LDL, VLDL-2 and VLDL-3 delivered at t = 0, hence the delivery rates are fixed as $\bar k_L = \bar k_2 = \bar k_3 = 0$. In the second scenario, the continuously-infused case, the concentrations of LDL, VLDL-2 and VLDL-3 in the extracellular medium depend on the body's transport processes, which we assume deliver a continuous supply of lipoproteins at rates $\bar k_L, \bar k_2, \bar k_3 > 0$. In the longer term, these rates of delivery have a greater influence on the state of the hepatocytes than the initial concentrations $\bar L_e(0), \bar V_{2e}(0)$, and $\bar V_{3e}(0)$. We present a numerical investigation of the single-bolus and the continuously infused models in Sects. 3.1 and 3.2 respectively, with a more theoretical analysis deferred to Sect. 4.

We have introduced the inequalities 0 ≤ p + Qq + Rr ≤ r _m because binding and unbinding to pits can only occur when the pit occupancy is between 0 and r _m . If p + Qq + Rr = r _m then we expect no further binding events to occur, thus $\bar a_{p,q,r}^+ = \bar \alpha_{p,q,r}^+ = \bar \beta_{p,q,r}^+ = 0$. To account for this, in simplest manner, we assume that $\bar a_{p,q,r}^+, \bar \alpha_{p,q,r}^+$ and $\bar \beta_{p,q,r}^+$ have the forms

$$\eqalign{ & \bar a_{p,q,r}^ + = {{\bar A}_ + }({r_m} - p - Qq - Rr),{\rm{ }}\bar \alpha _{p,q,r}^ + = {{\bar B}_ + }({r_m} - p - Qq - Rr),{\rm{ and }}\bar \beta _{p,q,r}^ + = {{\bar D}_ + }({r_m} - p - Qq - Rr) \cr & \bar a_{p,q,r}^ - = \bar A - p,{\rm{ }}\bar \alpha _{p,q,r}^ - = \bar B - q,{\rm{ }}\bar \beta _{p,q,r}^ - = \bar D - {r_{}} \cr} $$

(2.5)

, so that the rate of adhesion is proportional to the remaining available space in the pit. The unbinding rates have the simpler forms

$$\bar a_{p,q,r}^ - = \bar A - p,{\rm{ }}\bar \alpha _{p,q,r}^ - = \bar B - q,{\rm{ }}\bar \beta _{p,q,r}^ - = \bar D - r$$

(2.6)

, since we assume that the rate of removal of LDL/VLDL-2/VLDL-3 particles is proportional to the number of LDL/VLDL-2/VLDL-3 particles already bound to a pit.

We now consider the mechanisms by which lipoprotein is transported across the cell membrane. We denote by $\bar N_{p,q,r} (\bar t)$ the number of pits per millilitre to which are bound p LDL particles, q VLDL-2 particles and r VLDL-3 particles at time $\bar t$.

Although it may be more natural to think of $\bar N_{p,q,r}$ as a number per surface area of cell, for consistency with all the other concentration variables, we will define $\bar N_{p,q,r}$ as a volumetric concentration. Then $\bar N_{0,0,0}(\bar t) = \bar N_0 (t)$ is the concentration of pits that are free from LDL, VLDL-2 and VLDL-3. Our mathematical model describes the evolution through time of $\bar N_{p,q,r} (\bar t)$ (0 ≤ p+ Qq + Rr ≤ r _m ), and the concentrations of external LDL, VLDL-2 and VLDL-3 particles ($\bar L_e, \bar V_{2e}$ and $\bar V_{3e}$), bound LDL, VLDL-2 and VLDL-3 particles ($\bar L_b, \bar V_{2b}$ and $\bar V_{3b}$), internalised LDL, VLDL-2 and VLDL-3 particles ($\bar L_i, \bar V_{2i}$ and $\bar V_{3i}$) and the cholesterol content released following LDL, VLDL-2 and VLDL-3 endocytosis ($\bar C$).

Next we consider the dynamics of the pits on the cell surface. We assume that empty pits are produced at a rate $\bar k_0(\bar t)$. LDL, VLDL-2 or VLDL-3 particles may bind to any pit that is not full, that is, those $\bar N_{p,q,r}$ with p + Qq + Rr < r _m . We also assume that any particle may unbind (dissociate) from a bound pit. Binding and unbinding can thus be described by

(2.7)

(2.8)

(2.9)

Formally, microscopic processes such as these are stochastic in nature, and subject to fluctuations; however, since we are concerned with simple properties of elementary reaction mechanisms averaged over many pits and many cells, over longer the timescales of interest to us, it is sufficient to consider only the statistically expected behaviour of the system. If we apply the law of mass action to reactions (2.7)–(2.9) then we arrive at the following set of equations

$$\eqalign{ & {{d{{\bar N}_0}} \over {d\bar t}} = {{\bar k}_0}(\bar t) - \bar a_{0,0,0}^ + {{\bar L}_e}{{\bar N}_0} - \bar \alpha _{0,0,0}^ + {{\bar V}_{2e}}{{\bar N}_0} - \bar \beta _{0,0,0}^ + {{\bar V}_{3e}}{{\bar N}_0} - {{\bar b}_0}{{\bar N}_0} \cr & + \bar a_{1,0,0}^ - {{\bar N}_{1,0,0}} + \bar \alpha _{0,1,0}^ - {{\bar N}_{0,1,0}} + \bar \beta _{0,0,1}^ - {{\bar N}_{0,0,1}} \cr} $$

(2.10)

$$\eqalign{ & {{d{{\bar N}_{p,q,r}}} \over {d\bar t}} = \bar a_{p - 1,q,r}^ + {{\bar L}_e}{{\bar N}_{p - 1,q,r}} + \bar \alpha _{p,q - 1,r}^ + {{\bar V}_{2e}}{{\bar N}_{p,q - 1,r}} + \bar \beta _{p,q,r - 1}^ + {{\bar V}_{3e}}{{\bar N}_{p,q,r - 1}} \cr & + \bar a_{p + 1,q,r}^ - {{\bar N}_{p + 1,q,r}} + \bar \alpha _{p,q + 1,r}^ - {{\bar N}_{p,q + 1,r}} + \bar \beta _{p,q,r + 1}^ - {{\bar N}_{p,q,r + 1}} \cr & - \bar a_{p,q,r}^ + {{\bar L}_e}{{\bar N}_{p,q,r}} - \bar \alpha _{p,q,r}^ + {{\bar V}_{2e}}{{\bar N}_{p,q,r}} - \bar \beta _{p,q,r}^ + {{\bar V}_{3e}}{{\bar N}_{p,q,r}} \cr & - \bar a_{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar \alpha _{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar \beta _{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar b{{\bar N}_{p,q,r}}, \cr & {\rm{ (0}} \le p{\rm{ + }}Qq + Rr < {r_m}{\rm{)}} \cr} $$

(2.11)

,

$$\eqalign{ & {{d{{\bar N}_{p,q,r}}} \over {d\bar t}} = \bar a_{p - 1,q,r}^ + {{\bar L}_e}{{\bar N}_{p - 1,q,r}} + \bar \alpha _{p,q - 1,r}^ + {{\bar V}_{2e}}{{\bar N}_{p,q - 1,r}} + \bar \beta _{p,q,r - 1}^ + {{\bar V}_{3e}}{{\bar N}_{p,q,r - 1}} \cr & - \bar a_{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar \alpha _{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar \beta _{p,q,r}^ - {{\bar N}_{p,q,r}} - \bar b{{\bar N}_{p,q,r}}, \cr & {\rm{ (}}p + Qq + Rr = {r_m}{\rm{)}} \cr} $$

(2.12)

, where $\bar b$ is the rate of internalisation of occupied pits and $\bar b_0 < \bar b$ the rate of internalisation of empty pits. Since we expect (p, q, r) to lie in the range 0 ≤ p ≤ r _m , 0 ≤ q ≤ r _m /Q, 0 ≤ r ≤ r _m /R, there will typically be r ³ _m /6QR $\bar N_{p,q,r}$ -variables (about 10⁵ equations, see Table 1 for parameter values). Rather than solving such a large system, in the next section we show how the number of dependent variables may be reduced dramatically.

Table 1 Characteristics and properties of a typical liver cell and a typical LDL particle

2.2 2.2 The macroscopic model

We recall that when formulating the model equations we have accounted for all possible cases of binding of p LDL particles, q VLDL-2 particles and r VLDL-3 particles to the pit. In order to reduce the number of model equations, we make a simplifying assumption: all pits may be characterised as either empty or occupied, an occupied pit is defined as having one or more lipoprotein particles bound to it. Accordingly, we denote by $\bar N (\bar t)$ the total number of pits in which the number of bound LDL, VLDL-2, VLDL-3 particles is nonzero, by $\bar N_0 (\bar t)$ the number of vacant pits, and by $\bar M_L (\bar t), \bar M_2 (\bar t)$ and $\bar M_3 (\bar t)$ the total amount of bound LDL, VLDL-2 and VLDL-3 respectively, that is,

$$\bar N(\bar t) = \sum\limits_{p,q,r} {{{\bar N}_{p,q,r}}} (\bar t),{\rm{ }}{\bar M_L}(\bar t) = \sum\limits_{p,q,r} {p{{\bar N}_{p,q,r}}} (\bar t),{\rm{ }}{\bar M_2}(\bar t) = \sum\limits_{p,q,r} {q{{\bar N}_{p,q,r}}} (\bar t),{\rm{ }}{\bar M_3}(\bar t) = \sum\limits_{p,q,r} {r{{\bar N}_{p,q,r}}} (\bar t)$$

(2.13)

where the summations are over all values of p, q, r such that 0 < p+ Qq + Rr ≤ r _m . We obtain our reduced system by summing appropriate multiples of Eqs. (2.11)–(2.12); this gives

$${{d\bar N} \over {d\bar t}} = \bar a_{0,0,0}^ + {{\bar L}_e}{{\bar N}_0} + \bar \alpha _{0,0,0}^ + {{\bar V}_{2e}}{{\bar N}_0} + \bar \beta _{0,0,0}^ + {{\bar V}_{3e}}{{\bar N}_0} - \bar b\bar N - ({{\bar A}_ - }{{\bar N}_{1,0,0}} + {{\bar B}_ - }{{\bar N}_{0,1,0}} + {{\bar D}_ - }{{\bar N}_{0,0,1)}}$$

(2.14)

,

$${{d{{\bar M}_L}} \over {d\bar t}} = {{\bar A}_ + }{{\bar L}_e}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar A}_ - }{{\bar M}_L} - \bar b{{\bar M}_L}$$

(2.15)

,

$${{d{{\bar M}_2}} \over {d\bar t}} = {{\bar B}_ + }{{\bar V}_{2e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar B}_ - }{{\bar M}_2} - \bar b{{\bar M}_2}$$

(2.16)

,

$${{d{{\bar M}_3}} \over {d\bar t}} = {{\bar D}_ + }{{\bar V}_{3e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar D}_ - }{{\bar M}_3} - \bar b{{\bar M}_3}$$

(2.17)

, together with Eq. (2.10). It is the special form of the rate coefficients (2.5)–(2.6) which makes this simplification possible. Other assumed forms for the rates (2.5)–(2.6) may make such a reduction impossible or lead to different reductions (for example, which require higher moments of $\bar N_{p,q,r}$ to be defined in addition to (2.14)).

In order to close the model we need to make some additional assumptions about the quantities $\bar N_{1,0,0}, \bar N_{0,1,0}$ and $\bar N_{0,0,1}$, that appear in Eqs. (2.10) and (2.14). We assume that the rate at which single particles unbind from pits with only one occupant is extremely small and may be neglected, thus we ignore the terms in the second line of (2.14). Hence, Eqs. (2.15)–(2.17) together with

$${{d{{\bar N}_0}} \over {d\bar t}} = {{\bar k}_0}(\bar t) - {{\bar A}_ + }{r_m}{{\bar L}_e}{{\bar N}_0} - {{\bar B}_ + }{r_m}{{\bar V}_{2e}}{{\bar N}_0} - {{\bar D}_ + }{r_m}{{\bar V}_{3e}}{{\bar N}_0} - {{\bar b}_0}{{\bar N}_0}$$

(2.18)

,

$${{d\bar N} \over {d\bar t}} = \bar A + {r_m}{{\bar L}_e}{{\bar N}_0} + {{\bar B}_ + }{r_m}{{\bar V}_{2e}}{{\bar N}_0} + {{\bar D}_ + }{r_m}{{\bar V}_{3e}}{{\bar N}_0} - \bar b\bar N$$

(2.19)

, constitute a closed system for $\bar N_0, \bar N, \bar M_L, \bar M_2$ and $\bar M_3$.

2.3 2.3 Modelling the intracellular processes

The intracellular processes that we consider when developing our model are summarised in Fig. 2. This diagram also summarises the reversible binding of LDL and VLDL particles to the cell surface. The production rate of new pits, $\bar k_0(\bar t)$, in Eq. (2.10) models their transport from an intracellular store to the cell surface. In more detail, we let $\bar R_i (\bar t)$ denote the number of pits in the internal store and assume $\bar k_0(\bar t) = \bar g \bar R_i (\bar t)$ for some constant $\bar g$ which is the rate at which pits are recycled to the surface. The number of pits in the internal store is influenced by three factors. Firstly a fraction, f, of internalised pits are recycled; secondly new pits are produced at a constant, relatively low rate (see [8] for details); and, finally, new pits are produced at a rate which is a decreasing function of the amount of cholesterol in the cell, as noted by Havekes et al. [10]. Combining these effects, we deduce that the time evolution of R _i may be described as follows

$${{d{{\bar R}_i}} \over {d\bar t}} = {{{{\bar k}_r}} \over {\bar K + \bar C}} + f(\bar b\bar N + {{\bar b}_0}{{\bar N}_0}) - \bar g{{\bar R}_i}$$

(2.20)

, where the term $\bar k_r/(\bar K + \bar C)$ models the combined effects of the small constant production and intracellular cholesterol-dependent production rates: the constant $\bar K$ is associated with de novo production and $\bar C (\bar t)$ denotes the internal cholesterol level at time $\bar t$.

It remains to model the intracellular cholesterol level of the cell, $\bar C$. Applying the law of mass action to reactions (2.1)–(2.3) we obtain

$${{d\bar C} \over {d\bar t}} = \bar \gamma {{\bar k}_{ld}}{{\bar L}_i} + \bar \delta {{\bar k}_{2d}}{{\bar V}_{2i}} + \bar \mu {{\bar k}_{3d}}{{\bar V}_{3i}} - \bar \lambda (\bar C - {{\bar C}_e})$$

(2.21)

. The final term appearing in Eq. (2.21) models the tendency of the cell to maintain cholesterol levels at some equilibrium value, $\bar C_e$. Note that this implies that once the intracellular cholesterol exceeds $\bar C_e$, the level can never drop below $\bar C_e$ as $\bar \lambda(\bar C - \bar C_e) = 0$ when $\bar C = \bar C_e$. The constant $\bar \lambda$ is the rate at which the cell is able to regulate its internal cholesterol level.

We now consider how the concentrations $\bar L_e, \bar V_{2e}, and \bar V_{3e}$ evolve. Applying the law of mass action to $\bar L_e, \bar V_{2e}$, and $\bar V_{3e}$ and referring to reactions (2.1)–(2.3) we find

$$W{{d{{\bar L}_e}} \over {d\bar t}} = W{{\bar k}_L} + \sum\limits_{p,q,r} {\bar a_{p,q,r}^ - {{\bar N}_{p,q,r}} - {{\bar L}_e}} \sum\limits_{p,q,r} {\bar a_{p,q,r}^ + {{\bar N}_{p,q,r}}} $$

(2.22)

$$W{{d{{\bar V}_{2e}}} \over {d\bar t}} = W{{\bar k}_2} + \sum\limits_{p,q,r} {\bar \alpha _{p,q,r}^ - {{\bar N}_{p,q,r}} - {{\bar V}_{2e}}} \sum\limits_{p,q,r} {\bar \alpha _{p,q,r}^ + {{\bar N}_{p,q,r}}} $$

(2.23)

$$W{{d{{\bar V}_{3e}}} \over {d\bar t}} = W{{\bar k}_3} + \sum\limits_{p,q,r} {\bar \beta _{p,q,r}^ - {{\bar N}_{p,q,r}} - {{\bar V}_{3e}}} \sum\limits_{p,q,r} {\bar \beta _{p,q,r}^ + {{\bar N}_{p,q,r}}} $$

(2.24)

where the summations are over all values of p, q, r such that 0 ≤ p+ Qq + Rr ≤ r _m . The quantity W has been introduced to account for the difference between the volume of the cells and the volume of the extra-cellular space containing the source of LDL and VLDL particles. Using the definitions of $\bar a_{p,q,r}, \bar a_{p,q,r}^-, \bar \alpha_{p,q,r}, \bar \alpha_{p,q,r}^-, \bar \beta_{p,q,r}$ and $\bar \beta _{p,q,r}$ given in Eqs. (2.5)–(2.6) we simplify (2.22)–(2.24) to

$$W{{d{{\bar L}_e}} \over {d\bar t}} = W{{\bar k}_L} - {{\bar A}_ + }{{\bar L}_e}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] + {{\bar A}_ - }{{\bar M}_L}$$

(2.25)

,

$$W{{d{{\bar V}_{2e}}} \over {d\bar t}} = W{{\bar k}_2} - {{\bar B}_ + }{{\bar V}_{2e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] + {{\bar B}_ - }{{\bar M}_2}$$

(2.26)

,

$$W{{d{{\bar V}_{3e}}} \over {d\bar t}} = W{{\bar k}_3} - {{\bar D}_ + }{{\bar V}_{3e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] + {{\bar D}_ - }{{\bar M}_3}$$

(2.27)

,

We already have Eqs. (2.15)–(2.17) for $\bar M_L = \bar L_b, \bar M_2 = \bar V_{2b}$ and $\bar M_3 = \bar V_{3b}$, hence we now apply the law of mass action to determine equations for $\bar L_i, \bar V_{2i}$ and $\bar V_{3i}$ in a similar manner. Referring to reactions (2.1)–(2.3) we deduce that $\bar L_i, \bar V_{2i}, \bar V_{3i}$ satisfy

$${{d{{\bar L}_i}} \over {d\bar t}} = \bar b{{\bar M}_L} - {{\bar k}_{ld}}{{\bar L}_i},{\rm{ }}{{d{{\bar V}_{2i}}} \over {d\bar t}} = \bar b{{\bar M}_2} - {{\bar k}_{2d}}{{\bar V}_{2i}},{\rm{ }}{{d{{\bar V}_{3i}}} \over {d\bar t}} = \bar b{{\bar M}_3} - {{\bar k}_{3d}}{{\bar V}_{3i}}$$

(2.28)

where the constants $\bar k_{ld}, \bar k_{2d}$ and $\bar k_{3d}$ are the rates at which cholesterol is released from internalised LDL, VLDL-2 and VLDL-3 particles.

In summary, we recapitulate the model equations

$${{d{{\bar N}_0}} \over {d\bar t}} = \bar g{\bar R_i} - ({\bar A_ + }{\bar L_e} + {\bar B_ + }{\bar V_{2e}} + {\bar D_ + }{\bar V_{3e}}){r_m}{\bar N_0} - {\bar b_0}{\bar N_0}$$

(2.29)

,

$${{d\bar N} \over {d\bar t}} = ({{\bar A}_ + }{{\bar L}_e} + {{\bar B}_ + }{{\bar V}_{2e}} + {{\bar D}_ + }{{\bar V}_{3e}}){r_m}{{\bar N}_0} - \bar b\bar N$$

(2.30)

,

$${{d{{\bar R}_i}} \over {d\bar t}} = {{{{\bar k}_r}} \over {\bar K + \bar C}} + f(\bar b\bar N + {{\bar b}_0}{{\bar N}_0}) - \bar g{{\bar R}_i}$$

(2.31)

,

$$W{{d{{\bar L}_e}} \over {d\bar t}} = W{{\bar k}_L} - {{\bar A}_ + }{{\bar L}_e}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] + {{\bar A}_ - }{{\bar M}_L}$$

(2.32)

,

$$ W\frac{{d\bar V_{2e} }} {{d\bar t}} = W\bar k_2 - \bar B + \bar V_{2e} [r_m (\bar N + \bar N_0 ) - \bar M_L - Q\bar M_2 - R\bar M_3 ] + \bar B - \bar M_2 $$

(2.33)

,

$$ W\frac{{d\bar V_{3e} }} {{d\bar t}} = W\bar k_3 - \bar D + \bar V_{3e} [r_m (\bar N + \bar N_0 ) - \bar M_L - Q\bar M_2 - R\bar M_3 ] + \bar D - \bar M_3 $$

(2.34)

,

$${{d{{\bar M}_L}} \over {d\bar t}} = {{\bar A}_ + }{{\bar L}_e}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar A}_ - }{{\bar M}_L} - \bar b{{\bar M}_L}$$

(2.35)

,

$${{d{{\bar M}_2}} \over {d\bar t}} = {{\bar B}_ + }{{\bar V}_{2e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar B}_ - }{{\bar M}_2} - \bar b{{\bar M}_2}$$

(2.36)

,

$${{d{{\bar M}_3}} \over {d\bar t}} = {{\bar D}_ + }{{\bar V}_{3e}}[{r_m}(\bar N + {{\bar N}_0}) - {{\bar M}_L} - Q{{\bar M}_2} - R{{\bar M}_3}] - {{\bar D}_ - }{{\bar M}_3} - \bar b{{\bar M}_3}$$

(2.37)

,

$${{d{{\bar L}_i}} \over {d\bar t}} = \bar b{{\bar M}_L} - {{\bar k}_{ld}}{{\bar L}_i}$$

(2.38)

,

$${{d{{\bar V}_{2i}}} \over {d\bar t}} = \bar b{{\bar M}_2} - {{\bar k}_{2d}}{{\bar V}_{2i}}$$

(2.39)

,

$${{d{{\bar V}_{3i}}} \over {d\bar t}} = \bar b{{\bar M}_3} - {{\bar k}_{3d}}{{\bar V}_{3i}}$$

(2.40)

,

$${{d\bar C} \over {d\bar t}} = \bar \gamma {{\bar k}_{ld}}{{\bar L}_i} + \bar \delta {{\bar k}_{2d}}{{\bar V}_{2i}} + \bar \mu {{\bar k}_{3d}}{{\bar V}_{3i}} - \bar \lambda (\bar C - {{\bar C}_e})$$

(2.41)

. With the benefit of hindsight, or with exceptional intuition, one might be able to write down such a system of equations as (2.29)–(2.41) directly from knowledge of the biological processes. However, in practise, such presumption often leads to the omission of important terms, and requires one to gloss over details such as the form of the rate coefficients (2.5)–(2.6). The approach presented above allows one to revisit this model, and consider constitutive relations.

The initial conditions for the system are

$$\eqalign{ & {{\bar L}_e}(0) = {{\bar L}_0},{\rm{ }}{{{\rm{\bar V}}}_{2e}}(0) = {{{\rm{\bar V}}}_{20}},{\rm{ }}{{{\rm{\bar V}}}_{3e}}(0) = {{{\rm{\bar V}}}_{30}},{\rm{ }}{{\bar M}_L}(0) = {{\bar M}_2}(0) = {{\bar M}_3}(0) = 0,{\rm{ }} \cr & {{\bar L}_i}(0) = {{{\rm{\bar V}}}_{2i}}(0) = {{{\rm{\bar V}}}_{3i}}(0) = 0,{\rm{ }}\bar C(0) = \theta {{\bar C}_e},{\rm{ }}{{\bar N}_0}(0) = {{\bar n}_0},{\rm{ }}\bar N(0) = 0,{\rm{ }}{{\bar R}_i}(0) = 0 \cr & \cr} $$

(2.42)

. The initial conditions (2.42) correspond to a situation where the cells are deprived of LDL, VLDL-2 and VLDL-3 so that there is no bound or internalised LDL, VLDL-2 and VLDL-3. Consequently all the pits on the cell surface are empty and pits are present at maximum level. The external concentrations of LDL, VLDL-2 and VLDL-3 are prescribed and the cholesterol level is at some fraction, 0 < θ < 1, of its equilibrium value. The initial condition for $\bar R_i$ assumes that in the fasted state, all pits are expressed on the surface of the cell, leaving none inside the cell.

2.4 2.4 Nondimensionalisation of the model

Typical values for the parameters are summarised in Tables 1 and 2. The derivations for these values are given in the Appendix.

Table 2 Dimensional parameters and their values

To nondimensionalise the model we make the following substitutions

$$\eqalign{ & t = \bar b\bar t,{\rm{ }}{N_0} = {{{{\bar N}_0}} \over {{{\bar n}_0}}},{\rm{ }}N = {{\bar N} \over {{{\bar n}_0}}},{\rm{ }}C = {{\bar C} \over {{{\bar C}_e}}},{\rm{ }}{R_i} = {{{{\bar R}_i}} \over {{{\bar n}_0}}}, \cr & {L_e} = {{{{\bar L}_e}} \over {{{\bar l}_0}}},{\rm{ }}{V_{2e}} = {{{{\bar V}_{2e}}} \over {{{\bar v}_0}}},{\rm{ }}{V_{3e}} = {{{{\bar V}_{3e}}} \over {{{\bar v}_0}}},{\rm{ }}{L_b} = {{{{\bar L}_b}} \over {{{\bar l}_0}}},{\rm{ }}{V_{2b}} = {{{{\bar V}_{2b}}} \over {{{\bar v}_0}}},{\rm{ }}{V_{3b}} = {{{{\bar V}_{3b}}} \over {{{\bar v}_0}}}, \cr & {M_L} = {{{{\bar M}_L}} \over {{{\bar n}_0}}},{\rm{ }}{M_2} = {{{{\bar M}_2}} \over {{{\bar n}_0}}},{\rm{ }}{M_3} = {{{{\bar M}_3}} \over {{{\bar n}_0}}},{\rm{ }}{L_i} = {{{{\bar L}_i}} \over {{{\bar l}_0}}},{\rm{ }}{V_{2i}} = {{{{\bar V}_{2i}}} \over {{{\bar v}_0}}},{\rm{ }}{V_{3i}} = {{{{\bar V}_{3i}}} \over {{{\bar v}_0}}} \cr} $$

(2.43)

, where overbars denote dimensional quantities and $\bar C_e$ is the cell's preferred cholesterol concentration. The timescale is that associated with pit internalisation, $\bar b^{-1}$. We introduce the following nondimensional parameter groupings

$$\eqalign{ & {b_0} = {{{{\bar b}_0}} \over {\bar b}},{\rm{ }}g = {{\bar g} \over {\bar b}},{\rm{ }}\lambda = {{\bar \lambda } \over {\bar b}},{\rm{ }}{k_r} = {{{{\bar k}_r}} \over {{{\bar n}_0}\bar b{{\bar C}_e}}},{\rm{ }}K = {{\bar K} \over {{{\bar C}_e}}},{\rm{ }} \cr & {A_ + } = {{{{\bar A}_ + }{{\bar L}_0}} \over {\bar b}},{\rm{ }}{B_ + } = {{{{\bar B}_ + }{{\bar V}_{20}}} \over {\bar b}},{\rm{ }}{D_ + } = {{{{\bar D}_ + }{{\bar V}_{30}}} \over {\bar b}},{\rm{ }}{A_ - } = {{{{\bar A}_ - }} \over {\bar b}},{\rm{ }} \cr & {B_ - } = {{{{\bar B}_ - }} \over {\bar b}},{\rm{ }}{D_ - } = {{{{\bar D}_ - }} \over {\bar b}}{\rm{, }} \cr & \gamma = {{\bar \gamma {{\bar L}_0}} \over {{{\bar C}_e}}},{\rm{ }}\delta = {{\bar \delta {{\bar V}_{20}}} \over {{{\bar C}_e}}},{\rm{ }}\mu = {{\bar \mu {{\bar V}_{30}}} \over {{{\bar C}_e}}},{\rm{ }}\psi = {{{{\bar n}_0}} \over {{{\bar L}_0}}},{\rm{ }}\phi = {{{{\bar n}_0}} \over {{{\bar V}_{20}}}},{\rm{ }}\chi = {{{{\bar n}_0}} \over {{{\bar V}_{30}}}},{\rm{ }} \cr & {k_L} = {{{{\bar k}_L}} \over {{{\bar L}_0}\bar b}},{\rm{ }}{k_2} = {{{{\bar k}_2}} \over {{{\bar V}_{20}}\bar b}},{\rm{ }}{k_3} = {{{{\bar k}_3}} \over {{{\bar V}_{30}}\bar b}},{\rm{ }}{k_{ld}} = {{{{\bar k}_{ld}}} \over {\bar b}},{\rm{ }}{k_{2d}} = {{{{\bar k}_{2d}}} \over {\bar b}},{\rm{ }}{k_{3d}} = {{{{\bar k}_{3d}}} \over {\bar b}} \cr} $$

(2.44)

. Values for these parameters are given in Table 3.

Table 3 Non-dimensional parameters and their values

Using the substitutions above we arrive at a nondimensional model, in which L _b = ψM _L , V _2b = φM ₂, V _3b = χM ₃, and

$${{d{N_0}} \over {dt}} = g{R_i} - ({A_ + }{L_e} + {B_ + }{V_{2e}} + {D_ + }{V_{3e}}){r_m}{N_0} - {b_0}{N_0}$$

(2.45)

,

$${{dN} \over {dt}} = ({A_ + }{L_e} + {B_ + }{V_{2e}} + {D_ + }{V_{3e}}){r_m}{N_0} - N$$

(2.46)

,

$${{d{R_i}} \over {dt}} = {{{k_r}} \over {K + C}} + f(N + {b_0}{N_0}) - g{R_i}$$

(2.47)

,

$$W{{d{L_e}} \over {dt}} = W{k_L} - {A_ + }\psi {L_e}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] + \psi {A_ - }{M_L}$$

(2.48)

,

$$W{{d{V_{2e}}} \over {dt}} = W{k_2} - {B_ + }\phi {V_{2e}}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] + \phi {B_ - }{M_2}$$

(2.49)

,

$$W{{d{V_{3e}}} \over {dt}} = W{k_3} - {D_ + }\chi {V_{3e}}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] + \chi {D_ - }{M_3}$$

(2.50)

,

$${{d{M_L}} \over {dt}} = {A_ + }{L_e}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] - {A_ - }{M_L} - {M_L}$$

(2.51)

,

$${{d{M_2}} \over {dt}} = {B_ + }{V_{2e}}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] - {B_ - }{M_2} - {M_2}$$

(2.52)

,

$${{d{M_3}} \over {dt}} = {D_ + }{V_{3e}}[{r_m}(N + {N_0}) - {M_L} - Q{M_2} - R{M_3}] - {D_ - }{M_3} - {M_3}$$

(2.53)

,

$${{d{L_i}} \over {dt}} = \psi {M_L} - {k_{ld}}{L_i}$$

(2.54)

,

$${{d{V_{2i}}} \over {dt}} = \phi {M_2} - {k_{2d}}{V_{2i}}$$

(2.55)

,

$${{d{V_{3i}}} \over {dt}} = \chi {M_3} - {k_{3d}}{V_{3i}}$$

(2.56)

,

$${{dC} \over {dt}} = \gamma {k_{ld}}{L_i} + \delta {k_{2d}}{V_{2i}} + \mu {k_{3d}}{V_{3i}} - \lambda (C - 1)$$

(2.57)

, together with the initial conditions

$$\eqalign{ & {L_e}(0) \in (0.1,{\rm{ 1), }}{V_{2e}}(0) \in \{ 0.125,{\rm{ }}0.5,{\rm{ 1\} , }}{V_{3e}}(0) \in \{ 0.125,{\rm{ }}0.5,{\rm{ 1\} , }} \cr & {M_L}(0) = 0,{\rm{ }}{M_2}(0) = 0,{\rm{ }}{M_3}(0) = 0,{\rm{ }}{L_i}(0) = 0,{\rm{ }}{V_{2i}}(0) = 0,{\rm{ }}{V_{3i}}(0) = 0,{\rm{ }} \cr & N(0) = 0,{\rm{ }}{N_0}(0) = 1,{\rm{ }}C(0) = \theta ,{\rm{ }}{R_i}(0) = 0 \cr} $$

(2.58)

. The sets of initial values for L _e , V _2e and V _3e indicate the ranges of values used in the experimental work of Jackson et al. [11] which we aim to reproduce in the next section. The source terms, k _L , k ₂ and k ₃ retained in Eqs. (2.48)–(2.50) will be set to zero for investigations of the single bolus model and retained, with positive constant values, for the continuous infusion model.

3 3 Numerical results

In this section we solve Eqs. (2.45)–(2.59) numerically in matlab using ode15s, a variable-order solver for stiff systems. We compare our simulations with experimental results of Brown and Goldstein [4] and Jackson et al. [11] and make several new predictions concerning LDL, VLDL-2 and VLDL-3 endocytosis in the case where lipoprotein is continuously introduced to the extracellular medium. The experiments of Jackson et al. [11], either had a combination of LDL and VLDL-2 or LDL and VLDL-3 present, never both VLDL-2 and 3. Hence our simulations will consider these two cases, our primarily focus being the competition between VLDL and LDL; however, later on, we also comment on the relative effects of the two types of VLDL, and speculate on how they might interact in a system in which LDL, VLDL-2 and VLDL-3 are all present.

3.1 3.1 Evaluation of the kinetics of the single bolus model

3.1.1 3.1.1 Comparison with experimental data: LDL only

We compare our numerical results against the experiments of Jackson et al. [11] and demonstrate that our model correctly captures the kinetics of lipoprotein metabolism. We simulate the in vitro experimental conditions in which monolayers of hepatocytes, having been deprived of cholesterol, are exposed to a single large dose of lipoprotein for a period of 5 h. We solve the model with k _L = k ₂ = k ₃ = 0 so that there is no delivery of lipoproteins apart from the initial dose given.

Our system of Eqs. (2.45)–(2.59) is first solved in the case where only LDL is present in the extracellular medium. Figure 3 shows the evolution in time of the number of empty, occupied and internalised pits (left) and the concentrations of external, bound and internalised LDL particles. Initially, we observe a linear growth in the number of occupied, and internalised pits. Over the timescale of minutes, this saturates, as almost all empty pits become occupied, and the number of occupied pits reduces slightly as more are internalised, the system then approaches a quasi-steady-state. The number of empty pits decreases to a minimum, before the number of internalised pits increases enough to provide a supply of empty pits to the cell surface.

Fig. 3

Left: a Simulation results for N₀, N, R _i and the total number of pits, N₀ + N + R _i plotted against time on log-log graph. Right: b Simulation results for the concentrations of external (L _e ), bound (L _b ) and internalised (L _i , scaled down by a factor of 10) LDL all plotted against time

The extracellular bath of LDL particles is so much larger than that which can be bound and internalised by the cells in 5 h, that no noticeable depletion of L _e occurs. The concentration of bound LDL rapidly reaches a steady-state, but that of internalised LDL is only just approaching a steady-state at the end of 5 h; see Fig. 3 for details. In order to replicate the results of Jackson et al. [11], we note the total amount of LDL taken up in the 5 h period, this is given by

$$W[{L_e}(0) - {L_e}(5{\rm{ h)]}}$$

(3.1)

We also note the proportion of free, bound, and internalised receptors for the given amount of L _e , and find 61% free, 9% bound and 30% internalised. This result agrees favourably with the model of Harwood and Pellarin [9], which predicts approximately 70% free, 10% bound and 20% internalised receptors at this extracellular concentration of LDL. A more detailed comparison of the model for uptake of LDL in the absence of VLDL is contained in [16].

3.1.2 3.1.2 Comparison with experimental data: VLDL and LDL

We now solve the system of Eqs. (2.45)–(2.59) in the case where the lipoprotein dose is a combination of LDL and either VLDL-2 or VLDL-3 to reproduce the results of Jackson et al. [11]. We perform a series of simulations. In each, the system is initiated with a certain amount of one type of VLDL present. The purpose of these experiments is to investigate the competition between VLDL and LDL for binding to the receptors, which results in less LDL being taken in by the hepatocytes when VLDL (of type 2 or 3) is present. Thus at the end of each simulation, we note the amount of LDL taken up, using (3.1), and calculate the percentage reduction in LDL uptake caused by that initial concentration of VLDL.

In the cases where VLDL is also present in the extracellular medium, the evolution of empty, occupied and internalised pits (N ₀, N, R _i ) is almost identical to that displayed in Fig. 3 (left panel). The concentrations of the various types of LDL/VLDL particles is more complicated. The dynamics of these concentrations are illustrated in Fig. 4 for exemplar values of initial VLDL concentrations. The concentrations of internalised LDL and VLDL (L _i , V _2i , V _3i , respectively) evolve over a very slow timescale; only becoming close to their steady-state values towards the end of the 5-h period. Meanwhile, the concentrations of bound LDL and VLDL reach steady-state in less than 30 min, and the extracellular concentrations L _e , V _2e , V _3e hardly change throughout the experiment due to the large difference in volume between the medium and cells (that is, W ≫ 1).

Fig. 4

Graphs of LDL/VLDL concentrations against time for the cases with and without VLDL present. Left LDL and VLDL-2; right LDL and VLDL-3. See text for more detailed explanation

The experimental data against which we compare results from the two models is shown in Fig. 5. The upper solid line, marked with circles denotes the reduction in LDL uptake due to the presence of VLDL-2, and the lower solid line (marked with diamonds) shows the reduction in LDL uptake due to VLDL-3 outcompeting LDL for receptors. At all concentrations, VLDL-3 causes a greater reduction in LDL uptake than a similar amount of VLDL-2. Larger amounts ofVLDL cause larger reductions in LDL uptake, though this effect is nonlinear and saturates (or softens) at larger VLDL concentrations; however, the effect is considerable, with upto a 70% reduction in LDL taken up by the HepG2 cells. These features are reproduced in our model simulations.

Fig. 5

Experimental data showing the change in LDL uptake given by different initial values of VLDL-2 (MUFA/PUFA) and VLDL-3 (SAFA) taken from Jackson et al. [11]

Values for nearly all our parameters have come from other experimental results, for full details, see Appendix A. Due to the variability of factors such as preparation and pre-starvation times, and non-uniformities in the temperature at which experiments are performed, it is reasonable to obtain figures which are the correct order of magnitude. Jackson et al. [11] in the caption of Fig. 2 quotes a take-up of 950 ng/mg cell protein, whereas Eq. (3.1) predicts LDL uptake of 2,030 ng/mg cell protein. The absolute amount of LDL taken up is overestimated by our model, by a systematic figure of about 2.14.

To make a more qualitative comparison of the results we plot scaled reductions in LDL uptake in Fig. 5, and note the excellent agreement in the relative changes of LDL uptake between the experimental and simulated results.

In Fig. 6 we plot the occupancy of a typical pit through time for three different simulations: the case where only LDL is present, the case in which LDL and VLDL2 are present, and the case involving both LDL and VLDL3. The lines marked with triangles denote the percentage occupancy of LDL-receptors, including those which are ‘occluded’ as well as those which have been bound. Due to their large size, when a VLDL-2 or a VLDL-3 particle binds to a receptor, they physically block other receptors, preventing LDL particles binding to these receptors; we refer to such hidden receptors as ‘occluded’. The numbers of LDL, VLDL-2, and VLDL-3 particles per pit are defined by

$${{{M_L}} \over {{N_0} + N}},{\rm{ }}{{{M_2}} \over {{N_0} + N}},{\rm{ }}{{{M_3}} \over {{N_0} + N}},{\rm{ and Occupancy = }}{{100({M_L} + Q{M_2} + R{M_3})} \over {{p_m}({N_0} + N)}}$$

(3.2)

respectively, the latter being the percentage of receptors which are unavailable for further binding. These quantities all reach quasi-steady-states at about t = 0.2 h, at which point, in the LDL only case, there are, on average, about 24 LDL particles in each pit (line of larger dots). The dashed line shows the number of LDL particles in each pit when VLDL-2 is present, this saturates at a value of about 18; in this case, the number of VLDL-2 particles in each pit is about 17, as indicated by the thin solid line. In the case where VLDL-3 is present, the number of LDL particles per pit drops to about 14 (dash-dotted line) and the number of VLDL-3 particles per pit is about 11 (dotted line). The total occupancy rises from 11% for the case of LDL only, to 27% for LDL with VLDL-2 present, to 42% for the case of LDL with VLDL-3 present. These figures included the occluded as well as bound receptors.

Fig. 6

Graphs of pit occupancy against time for the cases with and without VLDL present. See text for full explanation, parameter values as given in Tables 2 and 3

Thus we note that (i) VLDL out-competes LDL for receptors, and that VLDL-3 is a stronger competitor than VLDL-2; (ii) but that the higher affinity of VLDL for receptors than LDL (due to VLDL containing apoE as well as apoB-100) leads to the usage of more receptors when VLDL is present. By “usage” we include both receptors bound to lipoprotein particles and receptors not bound but occluded by VLDL particles. When only LDL is present, typically only 26 of the 200 receptors are utilised when the pit is internalised; however, when VLDL-2 (or -3) is present, about 40 receptors have particles bound to them, and as many as a further 50 are prevented from binding to LDL as they are hidden by VLDL particles.

3.1.3 3.1.3 The effect of larger concentrations of VLDL-2 or VLDL-3

The case of initial concentrations of VLDL larger than that used in the experiments of Jackson et al. [11] has been analysed using the mathematical model. The predicted results are shown in Fig. 7, in which the uppermost dashed line with left-pointing triangles corresponds to the effect of VLDL-2 on LDL uptake, and the lowest dashed curve with right-pointing triangles denotes the effect of VLDL-3 on LDL uptake. These curves show that at higher concentrations of VLDL, the amount LDL taken up continues to fall further. Whilst the curves for VLDL-2 inhibition and VLDL-3 inhibition appear to converge, VLDL-3 remains a stronger inhibitor than VLDL-2 at all concentrations. At large enough concentrations the LDL uptake can be reduced below 10% of its level when no VLDL is present.

Fig. 7

Extension of Fig. 5 to larger VLDL concentrations. The graph shows the change in LDL uptake predicted for given initial values of VLDL-2 (MUFA/PUFA) andVLDL-3 (SAFA), and mixtures of VLDL-2 and 3. The graph includes the experimental data taken from Jackson et al. [11], but also includes predictions from the mathematical model for much larger initial VLDL concentrations, and initial conditions which contain mixtures of VLDL-2 and 3

3.1.4 3.1.4 Three-component mixtures of LDL, VLDL-2 and VLDL-3

Also illustrated in Fig. 7 are the predicted reductions in LDL uptake caused by mixtures of VLDL-2 and VLDL-3. In these systems there is a three-way competition between LDL, VLDL-2 and VLDL-3 for the same receptors.

Technically, there may be some higher-order steric effects not included in (2.5), such as receptors which are accessible to LDL particles but not to one or other or both types of VLDL particle. However, we deem the complexity introduced by such considerations not necessary for the study presented here. To keep the simplicity of the model, we assume that the steric effect of the different types of VLDL particle on each other are the same as on LDL particles, that is, the model simply keeps track of the number of available LDL receptors in a pit, and these receptors are assumed to be equally available to LDL and VLDL particles. The fit shown in Fig. 5 shows that such effects are not required to achieve good agreement in the case of LDL and one type of VLDL particle.

We consider the same range of total apoB-100 concentrations as in Sect. 3.1.3, and consider mixtures of equal numbers of VLDL-2 and 3 (denoted ‘Sim with VLDL-2&3’ and marked by a dashed line with crosses), and cases with 75% VLDL-2 and 25% VLDL-3 (denoted by a dotted line and triangles and ‘Sim with VLDL-2(3)’) and 25% VLDL-2 and 75% VLDL-3 (denoted by a dotted line with inverted triangles and the label ‘Sim with VLDL-3(2)’).

As might be expected, the effects of mixtures of VLDL 2 and 3 on LDL uptake lie between the curves for pure VLDL species. However, there is a noticeable asymmetry in their placement. The curve for an equal mixture of VLDL-2 and 3 lies considerably closer to the curve for pure VLDL-3 than to the curve for pure VLDL-2. Also the curve corresponding to a 75/25 split of VLDL-3/2 is extremely close to the curve for pure VLDL-3, indicating that a slight switch from SAFA-rich meal to a meal lower in SAFA and some PUFA/MUFA will make little difference to LDL uptake. It is only when the SAFA content of the meal is less than that of MUFA/PUFA that a subsequent replacement of VLDL-3 by VLDL-2 will cause a significant increases in LDL uptake.

3.2 3.2 The continuously-infused model

In this section we study the behaviour of our model when k _L , k ₂, k ₃ are positive in order to gain insight into the response of the liver to a continuous supply of lipoprotein. We show how the behaviour of the system at larger times (2–12 h) depends on the sizes of the rates k _L , k ₂ and k ₃) and we also show that the behaviour when k _L , k ₂, k ₃ ≪ 1 differs markedly from that when k _L , k ₂, k ₃ are larger. Since, in this case, the source of L _e is an input flux (as is the source of V _e2 andV _e3), we use the initial conditions L{nue}(0) = 0, V _e2(0) = 0, V _e3(0) = 0. We show that this change in behaviour occurs as a critical surface is crossed in (k _L , k ₂, k ₃)-space.

In all the above sections, the parameter W has been set to 1,500 as the ratio of the volume containing the extracellular LDL and VLDL to the total volume of cells. In the present section, we set W = 3, since the corresponding ratio in the human body is that of the blood plasma (∼4.7 l) to that of the liver (∼1.6 l).

3.2.1 3.2.1 Smaller lipoprotein delivery rates

We set the delivery rates to be small and calculate the predicted evolution of all the concentrations in the model through a time period of 5 h. We observe that all quantities approach steady-states. The results are shown in Fig. 8. A steady-state is approached only if the input rates k _L , k ₂, k ₃ are small enough: above a critical level, a steady-state cannot be attained; we take ‘small’ to be small in comparison with these critical input rates, k _Lc , k _2c , k _3c , which will be defined later (see Sect. 4.2 for details). In particular, in the left of Fig. 8, we set k _L = 0.1k _Lc , k ₂ = 0.05k _2c , k ₃ = 0.05k _3c . On the right-hand-side of Fig. 8, we display the results for an intermediate set of input rates, k _L = 0.3k _Lc , k ₂ = 0.15k _2c , k ₃ = 0.15k _3c which are still small enough that the system approaches a steady-state.

Fig. 8

Top graphs of the relative numbers of occupied (N), internal (R _i ) and empty pits (N₀), together with the numbers of receptors occupied by LDL (EquationSource% MathType!MTEF!2!1!+- % feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqr1ngB % PrgifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-Hhbbf9v8qqaqFr0x % c9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq0-yq-He9q8qqQ8fr % Fve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaqada % qaamaalaaabaGaamytamaaBaaaleaacaWGmbaabeaaaOqaaiaad6ea % daWgaaWcbaGaaGimaaqabaGccqGHRaWkcaWGobaaaaGaayjkaiaawM % caaaaa!3E8C! <InlineEquation ID="IE1"><InlineMediaObject> <ImageObject FileRef="285_2008_Article_205_TeX2GIFIE1.gif" Format="GIF" Color="BlackWhite" Type="Linedraw" Rendition="HTML"/> </InlineMediaObject><EquationSource Format="TEX"><![CDATA[$$ \bar L_e $$ ), VLDL-2 and VLDL-3 particles (${{{QM_2}} \over {{N_0} + N}}$ and ${{{RM_3}} \over {{N_0} + N}}$, respectively), plotted against time. Centre graphs of extracellular, bound and internalised LDL (L _e , L _b , L _i , respectively), and internalised VLDL particles (V_2i and V_3i ) plotted against time. Bottom: graphs of bound and extracellular VLDL concentrations (φM₂, χM₃, V_2e , and V_3e ) together with internal cholesterol level (C), again plotted against time. Parameter values: in all cases W = 3, left: k _L = k _Lc /10, k₂ = k_2c /20, k₃ = k_3c /20; right: k _L = 3k _Lc /10, k₂ = 3k_2c /20, k₃ = 3k_3c /20. All other parameter values are as in Table 3

Examining the graphs at the top of Fig. 8 we see that even at the smaller input rates, the number of empty pits (N ₀) asymptotes to a small value (below 0.1), while the number of occupied pits N approaches 0.7 and the number of internalised pits R _i plateaus at about 0.3. The total occupancy of receptors is less than 10% for the smaller input rate and about 20% for the larger input rate.

Turning to the central and lower panels of Fig. 8, we note that L _i takes the longest time to reach steady-state, only just reaching a plateau after 5 h. For the larger input rate this occurs at L _i = 13. The quantities L _e , L _b , V _2e , V _3e , V _2b , V _3b all reach steady-state by first overshooting their steady-state values and then approaching them from above, whereas the convergence of C, L _i , V _2i , V _3i is monotone.

3.2.2 3.2.2 Larger lipoprotein delivery rates

To investigate the system's behaviour when the lipoprotein delivery rates are larger, we set k _L = k _Lc , k ₂ = ½ k _2c , k ₃ = ½ k _3c in Eqs. (2.45)–(2.59). Figure 9 shows the results of this supercritical set of input rates, in which the concentrations of extracellular LDL, VLDL-2/3 (L _e , V _2e , V _3e ) all grow linearly in time. This behaviour shows that the system as a whole has no steady-state. However, variables associated with intracellular concentrations appear to attain steady-states after about 6 h.

Fig. 9

Top left graphs of the relative numbers of occupied (N), internal (R _i ) and empty pits (N₀), together with the numbers of receptors occupied by LDL (${{{M_L}} \over {{N_0} + N}}$), VLDL-2 and VLDL-3 particles (${{{QM_2}} \over {{N_0} + N}}$ and ${{{RM_3}} \over {{N_0} + N}}$, respectively), plotted against time. Lower left graphs of extracellular, and internalised LDL and VLDL particles (L _e , V_2e , V_3e , L _i , V_2i and V_3i ) plotted against time. Lower right: graphs of bound LDL and VLDL (ψM _L , φM₂, χM₃) together with internal cholesterol level (C), again plotted against time. Parameter values: in all cases W = 3, k _L = k _Lc , k₂ = k_2c /2, k₃ = k_3c /2; All other parameter values are as in Table 3

The average pit occupancy approaches a steady state value of unity, indicating that all receptors are full all the time, and the number of empty pits asymptotes to zero. The cell thus approaches a steady-state where it is processing VLDL and LDL at a maximum throughput rate.

Despite the nondimensional extracellular concentration of LDL always exceeding that of VLDL (of both types), the pit occupancies show that there are approximately equal numbers of receptors covered by each of the three types of lipoproteins. This is due to the lipoprotein adhesion rates for VLDL-2/3 being greater than those for LDL.

In summary, our results suggest that when the rate of lipoprotein delivery to the pits is large, for example, during the post-prandial period [6], in obesity [5] and in type 2 diabetes [1], the presence of large amounts of VLDL particles, which outcompete LDL for LDL receptors causes a significant reduction in LDL uptake and consequently a lower level of intracellular cholesterol. This explains why a lower rate of hepatic LDL uptake may be observed in cases where there is overproduction of VLDL.

4 4 Steady-state solutions

In this section we determine the steady state to which the system evolves at large times in order to confirm the longtime behaviour of the numerical solutions presented in Sect. 3. Whilst we focus on the cases where k _L , k ₂, k ₃ > 0, we initially consider the single bolus model (k _L = k ₂ = k ₃ = 0) as this analysis is straightforward and provides a necessary condition relating the parameter values. For the continuously-infused model, a steady-state solution only exists for a certain range of input rates of lipoprotein. For values outside this range, only a pseudo-steady-state exists. By pseudo-steady state we mean a state in which those variables describing the cell approach steady values, but the extracellular concentrations of LDL and VLDL grow linearly with time. In the next two subsections we study all these states.

4.1 4.1 Single bolus model

With k _L = k ₂ = k ₃ = 0, we determine the steady-state solution by setting the time derivatives in Eqs. (2.45–(2.57) to zero. It is straightforward to show that at equilibrium we have

$${L_e} = {V_{2e}} = {V_{3e}} = 0,{\rm{ }}{M_L} = {M_2} = {M_3} = 0,{\rm{ }}{L_i} = {V_{2i}} = {V_{3i}} = 0$$

(4.1)

,

$$N = 0,{\rm{ }}C = 1,{\rm{ }}{N_0} = 1,{\rm{ }}{R_i} = {{{b_0}} \over g}$$

(4.2)

, and

$${b_0}(1 - f) = {{{k_r}} \over {K + 1}}$$

(4.3)

. Equation (4.3) places a constraint on b ₀, f, k _r and K which can be used to estimate one of the parameters involved in (4.3) if the other three are known. Physically, this equation states that, at the steady-state, the loss of receptors due to imperfect recycling (LHS of (4.3) with f < 1) following internalisation (at rate b ₀) is balanced by the creation of new receptors (RHS of (4.3)).

As expected, since there is no delivery of lipoproteins after t = 0, the system settles to a state in which all the extracellular, bound and internalised lipoprotein concentrations approach zero. The pits on the cell surface are empty, and the intracellular cholesterol level is maintained at some steady value. Empty pits are internalised by endocytosis at a constant slow rate, most are recycled, and a few new pits are manufactured at a rate to replenish those that are not recycled and thereby maintain the steady-state. This behaviour is consistent with the long-time behaviour of the numerical results presented in Sect. 3.

4.2 4.2 The continuously infused model

4.2.1 4.2.1 General formulation

For small nonzero values of k _L , k ₂ and k ₃ we expect the system to tend to a non-trivial steady state, which is similar to (4.1)–(4.3). For larger values of k _L , k ₂ and k ₃ we find the dynamics are different: the liver cells become overloaded with external LDL, VLDL-2 and VLDL-3 causing the concentrations of extracellular lipoproteins grow linearly in time. There is thus a separatrix in (k _L , k ₂, k ₃)-space such that on one side the system evolves to a steady-state whilst on the other side there is linear growth in the levels of extracellular lipoproteins.

Setting the time derivatives to zero in Eqs. (2.45)–(2.57) with k _L , k ₂ and k ₃ not all zero, we obtain the following expressions for the steady state concentrations of the variables

$$\eqalign{ & {M_L} = {{W{k_L}} \over \psi },{\rm{ }}{M_2} = {{W{k_2}} \over \phi },{\rm{ }}{M_3} = {{W{k_3}} \over \chi },{\rm{ }} \cr & {L_i} = {{W{k_L}} \over {{k_{ld}}}},{\rm{ }}{V_{2i}} = {{W{k_2}} \over {{k_{2d}}}},{\rm{ }}{V_{3i}} = {{W{k_3}} \over {{k_{3d}}}},{\rm{ }} \cr & C = 1 + {{W(\gamma {k_L} + \delta {k_2} + \mu {k_3})} \over \lambda } \cr} $$

(4.4)

,

$${N_0} = {{g{R_i}} \over {{A_ + }{r_m}{L_e} + {B_ + }{r_m}{V_{2e}} + {D_ + }{r_m}{V_{3e}} + {b_0}}}$$

(4.5)

,

$$N = {{g{R_i}{r_m}({A_ + }{L_e} + {B_ + }{V_{2e}} + {D_ + }{V_{3e}})} \over {{A_ + }{r_m}{L_e} + {B_ + }{r_m}{V_{2e}} + {D_ + }{r_m}{V_{3e}} + {b_0}}}$$

(4.6)

, where

$$g{R_i} = {{\lambda {k_r}} \over {(1 - f)(\lambda K + \lambda + W(\gamma {k_L} + \delta {k_2} + \mu {k_3}))}}$$

(4.7)

, and L _e , V _2e and V _3e remain to be determined.

4.2.2 4.2.2 The critical surface in (k_L, k₂, k₃)-space

The surface across which steady-state solutions cease to exist can now be defined. As (k _L , k ₂, k ₃) approach the critical surface, the concentrations L _e , V _2e , V _3e diverge, leading to N ₀ → 0 (from Eq. (4.5)). On the critical surface we have that $r_m N - M_L - QM_2 - RM_3 = 0$, which implies

$${{{r_m}{k_r}\lambda } \over {(1 - f)[\lambda K + \lambda + W(\gamma {k_L} + \delta {k_2} + \mu {k_3})]}} = {{W{k_L}} \over \psi } + {{W{k_2}} \over \phi } + {{W{k_3}} \over \chi }$$

(4.8)

.

In the case of pure lipoprotein delivery, the maximum rates are given as follows: in the case k ₂ = 0 = k ₃, the condition that the LDL delivery rate leads to a steady-state is

$${k_L} < {k_{Lc}}: = {{\lambda (K + 1)} \over {2\gamma W}}\left( { - 1 + \sqrt {1 + {{4\gamma \psi {r_m}{k_r}} \over {\lambda (1 - f){{(K + 1)}^2}}}} } \right) \sim {{\psi {r_m}{k_r}} \over {W(1 - f)(K + 1)}}$$

(4.9)

, when k _L = 0 = k ₃ we have the condition

$${k_2} < {k_{2c}}: = {{\lambda (K + 1)} \over {2\delta W}}\left( { - 1 + \sqrt {1 + {{4\delta \phi {r_m}{k_r}} \over {Q\lambda (1 - f){{(K + 1)}^2}}}} } \right) \sim {{\phi {r_m}{k_r}} \over {QW(1 - f)(K + 1)}}$$

(4.10)

, whereas when k _L = 0 = K ₂ we have

$${k_3} < {k_{3c}}: = {{\lambda (K + 1)} \over {2\mu W}}\left( { - 1 + \sqrt {1 + {{4\mu \chi {r_m}{k_r}} \over {R\lambda (1 - f){{(K + 1)}^2}}}} } \right) \sim {{\chi {r_m}{k_r}} \over {RW(1 - f)(K + 1)}}$$

(4.11)

. The approximations are based on the assumption that the fraction inside the square root is small. For more general values of k ₂, k ₃, there is a critical k _Lc = k _Lc (k ₂, k ₃) which is obtained by solving the quadratic (4.8) and is graphed in Fig. 10. This surface is in fact part of a saddle (see Appendix B); although due to its small curvature, it appears planar.

Fig. 10

Graph showing the boundary of the region of k _L , k ₂, k ₃ space in which a steady state exists. The region is bound by the surface shown and the planes k _L = 0, k ₂ = 0 and k ₃ = 0

4.2.3 4.2.3 Dynamic behaviour for general input rates k_L, k₂, k₃

We define F by $F = r_m (N + N_0)$ and use (4.5)–(4.7) to obtain

$$F = {{{r_m}\lambda {k_r}({A_ + }{r_m}{L_e} + {B_ + }{r_m}{V_{2e}} + {D_ + }{r_m}{V_{3e}} + 1)} \over {(1 - f)(\lambda K + \lambda + W(\gamma {k_L} + \delta {k_2} + \mu {k_3}))({A_ + }{r_m}{L_e} + {B_ + }{r_m}{V_{2e}} + {D_ + }{r_m}{V_{3e}} + {b_0})}}$$

(4.12)

. Next, we obtain the following expressions for L _e , V _2e and V _3e by substituting equations (4.4)–(4.7) into Eqs. (2.48)–(2.50) yielding

$${{W{k_L}(1 + {A_ - })} \over {{A_ + }\psi }} = {L_e}\left( {F - {{W{k_L}} \over \psi } - {{QW{k_2}} \over \phi } - {{RW{k_3}} \over \chi }} \right)$$

(4.13)

,

$${{W{k_2}(1 + {B_ - })} \over {{B_ + }\phi }} = {V_{2e}}\left( {F - {{W{k_L}} \over \psi } - {{QW{k_2}} \over \phi } - {{RW{k_3}} \over \chi }} \right)$$

(4.14)

,

$${{W{k_3}(1 + {D_ - })} \over {{D_ + }\chi }} = {V_{3e}}\left( {F - {{W{k_L}} \over \psi } - {{QW{k_2}} \over \phi } - {{RW{k_3}} \over \chi }} \right)$$

(4.15)

, In general it is not possible to construct explicit analytical expressions for L _e , V _2e and V _3e . However, we can make progress in three special cases.

One is the case of small lipoprotein delivery rates, where an expansion around the trivial steady-state (4.1)–(4.2) can be obtained, as detailed in the next subsection; another special case is that of input rates close to the critical surface (4.8) in(k _L , k ₂, k ₃)-space. Here, the cells adapt to the steady-state given by Eqs. (4.4)–(4.5) together with N ₀ ≪ 1, N = gR _i and R _i given by (4.7). The extracellular concentrations L _e , V _2e , V _3e are large, and solve Eqs. (4.13)–(4.15) (simple closed-form analytical expressions for L _e , V _2e and V _3e do not, in general, exist). The final case that merits discussion is where (k _L , k ₂, k ₃) lie above the critical surface (4.8). This scenario is analysed in Sect. 4.2.5.

4.2.4 4.2.4 Small lipoprotein delivery rates, k} _L , k ₂, k ₃ ≪ 1

In the limit 0 < k _L , k ₂, k ₃ ≪ 1, we have F ∼ λk _r r _m /(1 − f)b ₀ λ(K + 1) and due to (4.3), this reduces to F ∼ r _m . It is thus possible to show that Eqs. (4.12)–(4.15) simplify to

$${L_e} = {{W{k_L}(1 + {A_ - })} \over {{A_ + }{r_m}\psi }},{\rm{ }}{V_{2e}} = {{W{k_2}(1 + {B_ - })} \over {{B_ + }{r_m}\phi }},{\rm{ }}{V_{3e}} = {{W{k_3}(1 + {D_ - })} \over {{D_ + }{r_m}\chi }}$$

(4.16)

. In addition, we retain (4.4), while in the limit 0 < k _L , k ₂, k ₃ ≪ 1 Eqs. (4.5) and (4.6) simplify to give

$$C = 1 + {{W(\gamma {k_L} + \delta {k_2} + \mu {k_3})} \over \lambda } = 1 + o(1),{\rm{ }}N = {{W{k_L}(1 + {A_ - })} \over \psi } + {{W{k_2}(1 + {B_ - })} \over \phi } + {{W{k_3}(1 + {D_ - })} \over \chi } \ll 1$$

(4.17)

.

To leading order, we also find R _i = b ₀/g and N ₀ = 1, which are identical to the ‘trivial’ steady-state (4.2). A higher-order expansion for small non-zero k _L , k ₂, k ₃ yields

$${R_i} = {{{b_0}} \over g}\left( {1 - {W \over {\lambda (K + 1)}}(\gamma {k_L} + \delta {k_2} + \mu {k_3})} \right)$$

(4.18)

,

$${N_0} = 1 - {{W(\gamma {k_L} + \delta {k_2} + \mu {k_3})} \over {\lambda (K + 1)}} - {W \over {{b_0}}}\left( {{{{k_L}(1 + {A_ - })} \over \psi } + {{{k_2}(1 + {B_ - })} \over \phi } + {{{k_3}(1 + {D_ - })} \over \chi }} \right)$$

(4.19)

. The above expressions reveal that L _e , V _2e and V _3e depend linearly on k _L , k ₂ and k ₃, respectively and R _i and N ₀ both decrease with increasing supply of lipoproteins. Such a solution is valid only at input rates smaller than those used in the numerical simulations displayed in the left-hand panels of Fig. 8.

4.2.5 4.2.5 Pseudo-steady-state for supercritical delivery rates

We recall from the numerical simulations that in the region where k _L , k ₂, k ₃ are above the critical surface, L _e , V _2e and V _3e rise linearly without bound while the other variables approach a steady state. The pseudo-steady-state is characterised by large-time asymptotic behaviour in which N ₀ → 0 whilst L _e , V _e2, V _e3 grow linearly in time, and other quantities approach constant values. More specifically, we make the ansatzs

$${L_e} \sim {k_L}(1 - {\tau _L})t + {\sigma _L},{\rm{ }}{V_{e2}} \sim {k_2}(1 - {\tau _2})t + {\sigma _2},{\rm{ }}{V_{e3}} \sim {k_3}(1 - {\tau _3})t + {\sigma _3}$$

(4.20)

, in which 0 < τ* < 1 are constants, yet to be determined, which describe the leading-order behaviour, and σ* are the first correction terms. By considering {1gdLza90i1}, {2gdLza90i2} and {3gdLza90i3} (Eqs. (2.48)–(2.53)), we find

$${M_L} \to {{{k_L}{\tau _L}} \over \psi },{\rm{ }}{M_2} \to {{{k_2}{\tau _2}} \over \phi },{\rm{ }}{M_3} \to {{{k_3}{\tau _3}} \over \chi }$$

(4.21)

;

$${L_i} \to {{{k_L}{\tau _L}} \over {{k_{ld}}}},{\rm{ }}{V_{2i}} \to {{{k_2}{\tau _2}} \over {{k_{2d}}}},{\rm{ }}{V_{3i}} \to {{{k_3}{\tau _3}} \over {{k_{3d}}}}$$

(4.22)

, the latter three arising from (2.54)–(2.56). Equations (2.57), (2.45)–(2.47) imply

$$C \to {C_\infty }: = 1 + {1 \over \lambda }(\gamma {k_L}{\tau _L} + \delta {k_2}{\tau _2} + \mu {k_3}{\tau _3})$$

(4.23)

,

$$N \to {{{k_r}} \over {(1 - f)(K + {C_\infty })}},{\rm{ }}{R_i} \to {{{k_r}} \over {g(1 - f)(K + {C_\infty })}}$$

(4.24)

,

$${N_0} \sim {{{k_r}} \over {{r_m}(K + {C_\infty })[{A_ + }{k_L}(1 - {\tau _L}) + {B_ + }{k_2}(1 - {\tau _2}) + {D_ + }{k_3}(1 - {\tau _3})]t}}{\rm{ as }}t \to \infty $$

(4.25)

This leaves the following three equations to determine τ _L , τ ₂ and τ ₃

$${{{\tau _e}(1 + {A^ - }{k_L}{\tau _e})} \over {{A_ + }\psi (1 - {\tau _e})}} = {{{\tau _2}(1 + {B^ - }{k_2}{\tau _2})} \over {{B_ + }\phi (1 - {\tau _2})}} = {{{\tau _3}(1 + {D^ - }{k_3}{\tau _3})} \over {{D_ + }\chi (1 - {\tau _3})}}$$

(4.26)

, and

$$(\lambda K + \lambda + \gamma {k_L}{\tau _L} + \delta {k_2}{\tau _2} + \mu {k_3}{\tau _3})\left( {{{{k_L}{\tau _L}} \over \psi } + {{{k_2}{\tau _2}Q} \over \phi } + {{{k_3}{\tau _3}R} \over \chi }} \right) = {r_m}{k_r}\lambda$$

(4.27)

. Given a value of τ _L in the range 0 < gt _L < 1, Eq. (4.26) determines a unique value of τ ₂ and τ ₃, each within the range 0 < τ _i < 1 (i = 2, 3). Low values of τ _L give low values of τ ₂ and τ ₃, and the LHS of (4.27) will be smaller than the RHS. Conversely, values of τ _L closer to unity imply larger values of τ ₂ and τ ₃, and the LHS of (4.27) will be larger than the RHS. The monotone behaviour of the LHS of (4.27) implies that there exists a unique solution for τ _L , and hence a unique solution of the whole system (2.45)–(2.57) of the form (4.20)–(4.25).

In vivo, these pseudo-steady-state solutions are clearly not sustainable: in situations where the system becomes inundated with lipoprotein other effects not included in our model will become important.

5 5 Conclusions

In this paper we have formulated and studied a mathematical model for lipoprotein endocytosis in liver cells. The motivation for this is to test the hypothesised mechanisms by which LDL endocytosis is inhibited by VLDL. In vitro experiments of Jackson et al. [11] have shown that the rate of LDL endocytosis is influenced by the presence of other lipoproteins, namely very low density lipoproteins (VLDL). VLDL particles bind to the LDLR via apolipoprotein E (apoE) molecules, thus competing with LDL for LDLR binding sites. VLDL isolated from individuals following consumption of single meals enriched in dietary fatty acids differentially compete with LDL for hepatic uptake, an effect which is attributed to variation in apoE content. VLDL isolated from individuals following saturated fat (SAFA)-rich meals carry an average of 3 apoE (VLDL-3) molecules per particle and better compete with LDL for hepatic uptake, than those isolated following polyunsaturated fatty acid (PUFA) and monounsaturated fatty acid (MUFA)-rich meals, which contain an average of 2 molecules of apoE per particle (VLDL-2). The agreement between the experimental results and the model presented herein (Fig. 5) support the explanation that LDL uptake is inhibited due to the larger VLDL particles binding to LDL receptors, reducing the availability of such receptors to LDL particles.

Our model is a system of ordinary differential equations which incorporates competition between LDL, VLDL-2 and VLDL-3 particles for binding to receptors in clathrin-coated pits on the surface of liver cells, as well as the internalisation and digestion of these lipoproteins and the consequential intracellular release of cholesterol. In addition, we have formulated compartmentalised equations for the number and content of pits to which the lipoproteins bind. To derive the model we first construct a detailed ‘microscopic’ model in which we account for the attachment of LDL, VLDL-2 and VLDL-3 particles to the coated pits on the surface of the hepatocyte. This model accounts for each possible combination of LDL, VLDL-2 and VLDL-3 particles attached to receptors in the pit. Hence our ‘microscopic model’ consists of a large coupled system of (∼10⁵) ordinary differential equations. By a judicious and physically realistic choice of the binding and unbinding rate parameters, we reduce the model to a system of just thirteen coupled ordinary differential equations. This ‘macroscopic model’ traces the average number of LDL, VLDL-2 and VLDL-3 particles bound to a coated pit and its investigation forms the basis of the remainder of the paper. The resulting model is studied in more detail in the remainder of this paper. Most of the model parameters have been found from the literature (for example, Harwood and Pellarin [9]), rather than by fitting to the data of Jackson et al. [11].

We solve the governing equations (2.45)–(2.59) numerically in several distinct cases: when the rates of lipoprotein delivery are zero and a large one-off delivery of lipoproteins is prescribed by the initial conditions; and, when the lipoprotein is delivered to the hepatocytes continuously through time. The former case resembles the experimental set up of Jackson et al. [11] and we refer to this case as the single bolus model. The latter case, where there is continuous supply of lipoproteins to the cells, is a better representation of the in vivo liver situation; we refer to this case as the continuously infused model.

For the single bolus model, our numerical results show excellent agreement with the experimental results of Jackson et al. [11], see Fig. 5. This shows that the model has correctly captured the competition effect by which LDL uptake is inhibited by the presence of VLDL particles. We have used the model to speculate on the behaviour of the system were larger initial concentrations of VLDL to be used, and to investigate the results of a system in which there is a three-way competition between LDL, VLDL-2 and VLDL-3. (The results of Jackson investigate two two-way competitions, one between LDL and VLDL-2 and the other between LDL and VLDL-3). The results of our simulations are shown in Fig. 7. Experiments using increased amounts of VLDL, and mixtures of the two types of VLDL would provide a test of our model.

The model also predicts the level of occupancy of pits, and Fig. 6 shows that even though there is competition for receptors, not all receptors acquire bound lipoprotein particles before internalisation. The preferential binding of apoE molecules on VLDL particles to LDL-R receptors causes VLDL to be over-represented in pits (compared to the relative presence of VLDL and LDL in the extracellular medium).

Simulations of the continuously infused model suggest that the behaviour of the solution depends on the rates of lipoprotein delivery. For small rates of delivery, all the concentrations and pit densities approach steady values at large times. At larger delivery rates, the system adopts a pseudo-steady-state in which the cell approaches a steady-state in which lipoprotein internalisation is maximised through all receptors being bound to upon internalisation. However, even in such a state, not all the delivered lipoprotein can be processed, so the extracellular concentrations grow linearly in time. We have illustrated these states using numerical simulations (see Fig. 9) and shown analytically how such states satisfy the governing equations (see Sect. 4.2.5).

Future mathematical modelling work will concentrate on adapting the model to account for the multiple forms which cholesterol is found within hepatocytes, investigating more realistic functional forms for the delivery rates k _L , k ₂ and k ₃, and whether a simpler model which relies only on receptor dynamics, rather than pit dynamics, explains the results as accurately [15].

Appendices

A Appendix: Parameter values

1.1 A1 Geometric parameters describing the cell

The number of receptors per cell varies between 20,000 and 50,000, (data for human fibroblasts taken from Brown and Goldstein [4]). Taking the median gives a typical value of 35,000 receptors per cell. This figure is similar to that obtained from Harwood and Pellarin [9], who quote a figure of 154 fm LDL receptors/mg cell protein. Using a conversion factor of 300 mg cell protein/ml, and a cell volume of 1 pl, we obtain 30,000 LDL receptors per HepG2 cell. The pit radius is typically of the order of 100 nm giving the the pit's projected area as 3.14 × 10⁻¹⁴m². A cell's surface area can be estimated as 2.85 × 10⁻¹⁰m², and typically 2% of a cell's surface ares is given over to pits. This implies that there are about 180 pits per cell, and each pit contains approximately $\bar r_m = 180$ receptors. Since the pits are hemispherical, each receptor covers about 3.4 × 10⁻¹⁶m².

LDL particles are spherical with radii of 10 nm [4], hence a cross-sectional area of 3 × 10⁻¹⁶ m² and so will cover no more than one receptor upon binding to a receptor in a pit. VLDL particles are larger, having radii in the range 15–40 nm. We assume VLDL-2 particles are at the lower end of this, (15 nm) and so cover 7 × 10⁻¹⁶ m², equivalent to two receptors—thus in addition to binding to a receptors, it will occlude a further receptor as well, preventing any other type of lipoprotein particle access to that receptor. VLDL-3 particles are larger still, we take an intermediate value of 20nm, which implies that they occupy 1.26 × 10⁻¹⁵ m², enough to cover 3.5 receptors. Therefore $\bar P = 1, \bar Q = 2, \bar R = 3.6$, and $\bar n_0 = 180$ pits per cell.

1.2 A2 Parameters describing extracellular concentrations

In deriving the model, we have implicitly assumed that concentration variables are measured in numbers of particles per unit volume. Thus we need to convert all the concentrations from mass per unit volume to number-weighted concentrations.

• $\bar L_0$: In the experimental set up by Jackson et al. [11] the initial concentration of LDL is 10 µg/ml cell medium. We convert this value to the number of particles by taking into account the molecular weight of apoB-100 (the integral protein of LDL and VLDL), that is, we write 10 µg/ml of cell medium $= {{10 \times {{10}^{ - 3}}g} \over {{\rm{molecular weight of apoB}} - 100}} \times {N_A} = 1.17 \times {10^{ - 13}}$ lipoprotein particles per ml cell medium.

• $\bar V_{20}$: In the experimental set up by Jackson et al. [11] three different values for the initial VLDL concentration are used: 2.5 µg per ml of cell medium, 10 µg per ml of cell medium and 20 µg per ml of cell medium. Using the same transformations as for $\bar L_0$ we obtain three values for the initial VLDL concentration to be respectively: 2.95 × 10¹², 1.17 × 10¹³ and 2.38 × 10¹³ lipoprotein particles per ml of cell medium.

• $\bar k_L, \bar k_2, \bar k3$: Respectively rates of LDL, VLDL-2 and VLDL-3 delivery. In the experimental protocols of Jackson et al. [11] these are zero, since the initial and one off delivery of lipoproteins is described by the initial conditions. In our in vivo predictions, we vary these and explore their impact on the model results.

1.3 A3 Kinetic parameters describing the binding of lipoprotein to the cell membrane

• $\bar A_+$: Rate of LDL binding to free receptors. In Harwood and Pellarin [9] (equation (1) and from the top line of Table 2) our $\bar A_+$ is denoted by k₁ and is given the value of k₁ = 4 × 10⁴ M⁻¹ s⁻¹. Since molarity, M, is the number of moles per litre, we have $\bar A_+ = 0.666 \times 10^{-16} ml s^{-1}$.

• $\bar B_+, \bar D_+$: Rate of VLDL-2 and VLDL-3 binding respectively. Whilst LDL particles have only one apoB-100 molecule, VLDL-2 particles have two apoE and one apoB-100 molecules, and VLDL-3 particles have three apoE molecules and one apoB-100. Experimental results by Minihane [12] suggest that the affinity of apoE to bind to the receptors is considerably larger than that of apoB-100. Thus we fit these parameters to be larger than A₊ and put $\bar B_+ = 4.5\bar A_+, \bar D_+ = 6.5 \bar A_+$.

• $\bar B_-, \bar D_-$: Since VLDL-2 has three apolipoproteins which may bind to LDL receptors in pits, we assume the unbinding rate is reduced from that for LDL by a factor of three. Similarly, VLDL-3 has four apolipoproteins which can form bonds, so we reduce its unbinding rate by a factor of four. Hence $\bar B_- = {1 \over 3} \bar A_-$ and $\bar D_- = {1 \over 4} \bar A_-$.

• $\bar b, \bar b_0$: Respectively the rate of internalisation of non-empty and empty pits. We take $\bar b$ to be the same as k₃ in Harwood and Pellarin [9], and to find a the value of $\bar b_0$ we take note of Basu et al.'s result [3] that $\bar b_0 = 2.27 \bar b$. Hence $\bar b = log 2/22 s^{-1}$ and $\bar b_0 = log 2/50 s^{-1}$.

• $\bar A_-$: Rate of LDL unbinding. From Harwood and Pellarin [9] (from the top figure in the penultimate column in Table 2, their k₂) we take $\bar A_- = 5.9 \times 10^{-4} s^{-1}$.

1.4 A4 Kinetic parameters describing the cell's internal processes

• $\bar k_{ld}, \bar k_{2d}, \bar k_{3d}$: Rate at which internalised LDL particles are converted to cholesterol. Brown and Goldstein [4] quote a time of 10 min for marked particle uptake to measurement of related cholesterol concentration. This time includes a number of mechanisms included in our model and we thus assume a figure of 5 min to be more realistic. Therefore we take $\bar k_{ld} = 1/300 s^{-1}$.

  In the absence of experimental data to suggest otherwise, we assume that k _2d = k _3d = k _ld , that is, LDL, VLDL-2 and VLDL-3 particles convert to cholesterol at the same rate.

• $\bar k_r, \bar K$: These parameters determine the rate of pit production by the cell. These parameters have been fitted to the experimental data of Brown and Goldstein [4] in modelling paper which focused on the endocytosis of LDL particles [16].

• $\bar g$: Rate of pit release from the internal store back to the cell surface. We assume that this parameter is the same as the rate of receptor recycling. In Harwood and Pellarin [9], Table 1, the rate constant k₅ gives the value $\bar g = 0.0108 s^{-1}$. This data is for Hep-G2 cells—the same line as used in the experiments of Jackson [11] that we are modelling.

• f: Fraction of internalised receptors returned to the cell surface. Results of Dunn et al. [7] suggest that 70%–100% of internalised receptors return to the cell surface following endocytosis. Therefore we take f ∈ [0.7,1], and typically use f = 0.9.

• $\bar \gamma$: Average cholesterol content per LDL particle. From Jackson et al. [11] we obtain $\bar \gamma = 3, 400$.

• $\bar \delta$: Average cholesterol content per VLDL-2 particle; from Jackson et al. [11] we have $\bar \delta = 3, 100$.

• $\bar \mu$: Average cholesterol content per VLDL-3 particle; from Jackson et al. [11] we have $\bar \mu = 3, 900$.

• $\bar \lambda$: Net rate cholesterol removal/synthesis. We use this single term to cover a combination of processes: (i) the continual slow exchange between the two types of cholesterol stored in the cell (free and esterified, the cycling conversion occurring over a 24 h timespan); (ii) the loss of free cholesterol through the manufacture of bile which is excreted by the liver; and (iii) de novo cholesterol synthesis. A fit to the experimental results on LDL endocytosis described in [16] suggests the value of 0.0033 s⁻¹.

B Appendix: analysis of the quadratic form (4.8)

In order to analyse the shape of the curve (4.8) it is helpful to rewrite it in the matrix form

$$({k_L},{k_2},{k_3})\left( {\matrix{ {\gamma \phi \chi } & {{{\chi (Q\gamma \psi + \delta \phi )} \over 2}} & {{{\phi (R\gamma \psi + \mu \chi )} \over 2}} \cr {{{\chi (Q\gamma \psi + \delta \phi )} \over 2}} & {Q\delta \psi \chi } & {{{\psi (R\delta \phi + Q\mu \chi )} \over 2}} \cr {{{\phi (R\gamma \psi + \mu \chi ){\rm{ }}} \over 2}} & {{{\psi (R\delta \phi + Q\mu \chi )} \over 2}} & {R\mu \psi \phi } \cr } } \right)\left( \matrix{ {k_L} \hfill \cr {k_2} \hfill \cr {k_3} \hfill \cr} \right)$$

(B1)

$$ + \lambda (K + {C_e})(\phi \chi ,{\rm{ }}Q\psi \chi ,{\rm{ }}R\psi \phi )\left( \matrix{ {k_L} \hfill \cr {k_2} \hfill \cr {k_3} \hfill \cr} \right) = {{\lambda {r_m}{k_r}\psi \phi \chi } \over {1 - f}}$$

(B2)

. The shape of the surface is found from the eigenvalues of the matrix, which we denote by θ ₁, θ ₂ and θ ₃. The characteristic polynomial is

$$0 = {\theta ^3} - (\gamma \phi \chi + Q\delta \psi \chi + R\mu \psi \phi ){\theta ^2} - {1 \over 4}\left( {{\chi ^2}{{(Q\gamma \psi - \delta \phi )}^2} + {\phi ^2}{{(R\gamma \psi - \mu \chi )}^2} + {\psi ^2}{{(Q\mu \chi - R\delta \phi )}^2}} \right)\theta $$

(B3)

, which is of the form aθ ³ +bθ ² +cθ = 0 with c < 0; hence one eigenvalue is θ ₃ = 0. Since c < 0 the other two eigenvalues are real and have opposite signs and the surface is a saddle (z = θ ₁ x ² + θ ₂ y ²).