Skip to main content
SpringerLink
Log in

Maximal Controllability for Boundary Control Problems

  • Published:
Applied Mathematics & Optimization Submit manuscript

Abstract

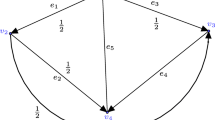
We develop a semigroup approach to abstract boundary control problems which allows to characterize the space of all approximately reachable states. We then introduce the “maximal reachability space” giving an upper bound for this space. The abstract results are applied to the flow in a network controlled in a single vertex.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Acquistapace, P., Terreni, B.: Infinite-horizon linear-quadratic regulator problems for nonautonomous parabolic systems with boundary control. SIAM J. Control Optim. 34, 1–30 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  2. Balakrishnan, A.V.: Applied Functional Analysis. Applications of Mathematics, vol. 3. Springer, New York (1976)

    MATH  Google Scholar 

  3. Balakrishnan, A.V.: Boundary control of parabolic equations: L−Q−R theory. In: Theory of Nonlinear Operators, Proc. Fifth Internat. Summer School, Central Inst. Math. Mech. Acad. Sci. GDR, Berlin, 1977, Abh. Akad. Wiss. DDR, Abt. Math. Naturwiss. Tech., 1978, vol. 6, pp. 11–23. Akademie-Verlag, Berlin (1978)

    Google Scholar 

  4. Bátkai, A., Piazzera, S.: Semigroups for Delay Equations, Research Notes in Mathematics, vol. 10. A K Peters Ltd., Nahch (2005)

    MATH  Google Scholar 

  5. Bensoussan, A., Da Prato, G., Delfour, M.C., Mitter, S.K.: Representation and Control of Infinite Dimensional Systems, 2nd edn., Systems & Control: Foundations & Applications. Birkhäuser Boston, Boston (2007)

    MATH  Google Scholar 

  6. Boulite, S., Idrissi, A., Maniar, L.: Robustness of controllability under some unbounded perturbation. J. Math. Anal. Appl. 304, 409–421 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  7. Boulite, S., Idrissi, A., Maniar, L.: Controllability of semilinear boundary control problems with nonlocal initial conditions. J. Math. Anal. Appl. 316, 566–578 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  8. Casarino, V., Engel, K.-J., Nagel, R., Nickel, G.: A semigroup approach to boundary feedback systems. Integral Equ. Oper. Theory 47, 289–306 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  9. Casarino, V., Engel, K.-J., Nickel, G., Piazzera, S.: Decoupling techniques for wave equations with dynamic boundary conditions. Discrete Contin. Dyn. Syst. 12, 761–772 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  10. Curtain, R.F., Zwart, H.J.: An Introduction to Infinite-Dimensional Linear Systems Theory. Texts Appl. Math., vol. 21. Springer, Berlin (1995)

    MATH  Google Scholar 

  11. Da Prato, G., Ichikawa, A.: Quadratic control for linear time-varying systems. SIAM J. Control Optim. 28, 359–381 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  12. Desch, W., Schappacher, W.: Some generation results for perturbed semigroups. In: Clément, P., Invernizzi, S., Mitidieri, E., Vrabie, I.I. (eds.) Semigroup Theory and Applications, Proceedings Trieste, 1987. Lect. Notes in Pure and Appl. Math., vol. 116, pp. 125–152. Dekker, New York (1989)

    Google Scholar 

  13. Desch, W., Lasiecka, I., Schappacher, W.: Feedback boundary control problems for linear semigroups. Isr. J. Math. 51, 177–207 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  14. Desch, W., Milota, J., Schappacher, W.: Least square control problems in nonreflexive spaces. Semigroup Forum 62, 337–357 (2001)

    MATH  MathSciNet  Google Scholar 

  15. Engel, K.-J., Nagel, R.: One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Math., vol. 194. Springer, Berlin (2000)

    MATH  Google Scholar 

  16. Engel, K.-J., Kramar Fijavž, M., Nagel, R., Sikolya , E.: Vertex control of flows in networks. J. Netw. Heterog. Media 3, 709–722 (2008)

    Article  MATH  Google Scholar 

  17. Fattorini, H.O.: Boundary control systems. SIAM J. Control 6, 349–385 (1968)

    Article  MATH  MathSciNet  Google Scholar 

  18. Flandoli, F., Lasiecka, I., Triggiani, R.: Algebraic Riccati equations with nonsmoothing observation arising in hyperbolic and Euler-Bernoulli boundary control problems. Ann. Mat. Pura Appl. 153, 307–382 (1988–1989)

    Article  MathSciNet  Google Scholar 

  19. Greiner, G.: Perturbing the boundary conditions of a generator. Houst. J. Math. 13, 213–229 (1987)

    MATH  MathSciNet  Google Scholar 

  20. Greiner, G.: Semilinear boundary conditions for evolution equations of hyperbolic type. In: Semigroup Theory and Applications, Trieste, 1987, Lecture Notes in Pure and Appl. Math., vol. 116, pp. 201–214. Dekker, New York (1989)

    Google Scholar 

  21. Greiner, G., Kuhn, K.G.: Linear and semilinear boundary conditions: the analytic case. In: Semigroup Theory and Evolution Equations, Delft, 1989, Lecture Notes in Pure and Appl. Math., vol. 135, pp. 193–211. Dekker, New York (1991)

    Google Scholar 

  22. Heijmans, H.J.A.M.: Semigroup theory for control on sun-reflexive Banach spaces. IMA J. Math. Control Inf. 4, 111–129 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  23. Jacob, B., Partington, J.R.: Admissibility of control and observation operators for semigroups: a survey. In: Current Trends in Operator Theory and ts Applications. Oper. Theory Adv. Appl., vol. 149, pp. 199–221. Birkhäuser, Basel (2004)

    Google Scholar 

  24. Kramar, M., Sikolya, E.: Spectral properties and asymptotic periodicity of flows in networks. Math. Z. 249, 139–162 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  25. Krause, S.: Zur Theorie linearer Randwertkontrollen. Ph.D. thesis, Universität Tübingen (1990)

  26. Lasiecka, I.: Unified theory for abstract parabolic boundary problems—a semigroup approach. Appl. Math. Optim. 6, 287–333 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  27. Lasiecka, I., Triggiani, R.: Dirichlet boundary control problem for parabolic equations with quadratic cost: analyticity and Riccati’s feedback synthesis. SIAM J. Control Optim. 21(1), 41–67 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  28. Lasiecka, I., Triggiani, R.: Abstract parabolic systems. In: Control Theory for Partial Differential Equations: Continuous and Approximation Theories. I. Encyclopedia of Mathematics and its Applications, vol. 74. Cambridge University Press, Cambridge (2000)

    Google Scholar 

  29. Lasiecka, I., Triggiani, R.: Abstract hyperbolic-like systems over a finite time horizon. In: Control Theory for Partial Differential Equations: Continuous and Approximation Theories. II. Encyclopedia of Mathematics and its Applications, vol. 75. Cambridge University Press, Cambridge (2000)

    Google Scholar 

  30. Lasiecka, I., Lions, J.-L., Triggiani, R.: Nonhomogeneous boundary value problems for second order hyperbolic operators. J. Math. Pures Appl. 65, 149–192 (1986)

    MATH  MathSciNet  Google Scholar 

  31. Lions, J.-L.: Optimal Control of Systems Governed by Partial Differential Equations. Die Grundlehren der mathematischen Wissenschaften, vol. 170. Springer, New York (1971). Translated from the French by S. K. Mitter

    MATH  Google Scholar 

  32. Malinen, J., Staffans, O.J.: Conservative boundary control systems. J. Differ. Equ. 231, 290–312 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  33. Malinen, J., Staffans, O.J.: Impedance passive and conservative boundary control systems. Complex Anal. Oper. Theory 1, 279–300 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  34. Malinen, J., Staffans, O.J., Weiss, G.: When is a linear system conservative? Q. Appl. Math. 64, 61–91 (2006)

    MATH  MathSciNet  Google Scholar 

  35. Nagel, R., Sinestrari, E.: Inhomogeneous Volterra integrodifferential equations for Hille-Yosida operators. In: Bierstedt, K.D., Pietsch, A., Ruess, W.M., Vogt, D. (eds.) Functional Analysis, Proceedings Essen, 1991. Lect. Notes in Pure and Appl. Math., vol. 150, pp. 51–70. Dekker, New York (1994)

    Google Scholar 

  36. Russell, D.L.: A unified boundary controllablity theory for hyperbolic and parabolic partial differential equations. Stud. Appl. Math. 52, 189–211 (1973)

    MATH  Google Scholar 

  37. Russell, D.L.: Controllablity and stabilizability theory for linear partial differential equations: recent progress and open problem. SIAM Rev. 20, 639–739 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  38. Salamon, D.: Infinite dimensional linear system with unbounded control and observation: a functional analytic approach. Trans. Am. Math. Soc. 300, 383–431 (1987)

    MATH  MathSciNet  Google Scholar 

  39. Sikolya, E.: Flows in networks with dynamic ramification nodes. J. Evol. Equ. 5, 441–463 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  40. Staffans, O.J.: Well-posed Linear Systems. Encyclopedia of Mathematics and its Applications, vol. 103. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  41. Staffans, O.J., Tucsnak, M., Weiss, G.: Well-posed linear systems—a survey with emphasis on conservative systems. Int. J. Appl. Math. Comput. Sci. 11, 7–33 (2001). Mathematical Theory of Networks and Systems (Perpignan, 2000)

    MATH  MathSciNet  Google Scholar 

  42. Triggiani, R.: Well-posedness and regularity of boundary feedback parabolic systems. J. Differ. Equ. 36, 347–362 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  43. Washburn, D.C.: A semigroup theoretic approach to modelling of boundary input problems. In: Distributed Parameter Systems: Modelling and Identification, Proc. IFIP Working Conf., Rome, 1976. Lecture Notes in Control and Informat Sci., vol. 1, pp. 446–458. Springer, Berlin (1978)

    Chapter  Google Scholar 

  44. Washburn, D.C.: A bound on the boundary input map for parabolic equations with application to time optimal control. SIAM J. Control Optim. 17, 652–671 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  45. Weiss, G.: Admissibility of unbounded control operators. SIAM J. Control Optim. 27, 527–545 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  46. Zabczyk, J.: Mathematical Control Theory: An Introduction. Birkhäuser, Basel (1992)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Pure and Applied Mathematics, University of L’Aquila, Via Vetoio (Coppito) 1, 67010, L’Aquila (AQ), Italy

    Klaus-Jochen Engel

  2. Faculty of Civil and Geodetic Engineering, University of Ljubljana, Jamova 2, 1000, Ljubljana, Slovenia

    Marjeta Kramar Fijavž

  3. Mathematics Institute, University of Tübingen, Auf der Morgenstelle 10, 72076, Tübingen, Germany

    Bernd Klöss & Rainer Nagel

  4. Department of Applied Analysis, Eötvös Loránd University Budapest, Pázmány Péter sétány 1/c, Budapest, 1117, Hungary

    Eszter Sikolya

Authors
  1. Klaus-Jochen Engel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marjeta Kramar Fijavž
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Bernd Klöss
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Rainer Nagel
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Eszter Sikolya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rainer Nagel.

Additional information

Communicating Editor: Irena Lasiecka.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Engel, KJ., Kramar Fijavž, M., Klöss, B. et al. Maximal Controllability for Boundary Control Problems. Appl Math Optim 62, 205–227 (2010). https://doi.org/10.1007/s00245-010-9101-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00245-010-9101-1

Keywords

Search

Navigation