1 Introduction

Nowadays air-conditioner is becoming a basic need in human life and in future, it is expected to play a vital role in our lives. Conventional air conditioning is based on vapour compression system utilizing HFC and HCFC which are harmful to the environment. Dai et al. [1] suggested that a desiccant cooling system is one of the best options to be used for air conditioning as it deals with the latent load and improves the indoor air quality (IAQ) by adsorbing moisture and preventing the contamination of air simultaneously. Desiccant dehumidifier running in open cycle and characterized by zero noise and low maintenance can be driven by solar energy or waste heat.

San and Hsiau [2] developed a one-dimensional (1-D) transient heat and mass transfer model to analyze the effect of axial heat conduction and mass diffusion on the performance of a desiccant wheel and discussed that Biot number (Bi) and NTU were two important parameters which affected the dehumidification ability. Dai et al. [1] evaluated the dehumidification performance of desiccant wheel on the basis of wave shape through wave analysis using psychrometric chart and discussed the effects of some important parameters, such as heat capacity, adsorption heat, rotational speed, regeneration temperature, thickness of the desiccant matrix and desiccant isotherm on the performance. Zhang and Niu [3] developed a 2D (axial direction and thickness direction) transient heat and mass transfer model for desiccant wheel and took into account both gas side and solid side resistance. They compared the performance of a desiccant wheel used in air dehumidification and enthalpy recovery on the basis of rotary speed, NTU and specific area. Niu and Zhang [4] developed a 2D (axial direction and thickness direction) transient heat and mass transfer model for desiccant wheel to calculate the optimum rotary speed for sensible heat recovery, latent heat recovery and air dehumidification which takes into account both gas side and solid side resistance. They also analyzed the effect of channel wall thickness on the optimum rotary speed used in air dehumidification and enthalpy recovery. Xuan and Radermacher [5] developed a 1-D transient model considering heat and mass transfer for moist air to investigate the performance of the wheel. Their simulation results revealed a significant effect of different regeneration temperatures, air flow rates and wheel speeds on the performance of wheel. Gao et al. [6] described a 1D mathematical model considering the heat and mass transfer in moist air as well as desiccant material to predict the transient and steady state transport in a desiccant wheel. The effect of desiccant thickness (felt thickness) and passage shape on the performance of a desiccant wheel was also investigated. Harshe et al. [7] presented a two-dimensional (2-D) steady-state model pertaining to a rotary desiccant wheel which included the mass and energy balance equations for the air streams and the desiccant wheel. The model was capable of predicting the steady-state behavior of a desiccant wheel for process, purge and regeneration sector. Sphaier and Worek [8] compared 1D and 2D mathematical models for both solid side and gas side resistance and found that 1D formulation could be used in desiccant wheel applications whereas a 2D model was needed for an enthalpy exchanger when thermal resistance in desiccant material was high. Ruivo et al. [9] described a 1D transient numerical solution of the conservation equations for heat, water vapour and adsorbed water inside the porous medium and found that surface diffusion was the most important mechanism of water transport within the porous medium by assuming a lumped heat capacitance model in the cross directions of the channel wall. Nia et al. [10] developed a 1D transient mathematical model by considering the heat and mass transfer for moist air and determined the optimum rotational speed by examining the outlet adsorption side humidity ratio to improve the performance of an adiabatic rotary dehumidifier. Golubovic et al. [11] evaluated the performance of a rotary dehumidifier on the basis of three sectors namely: purge, process and regeneration. The performance of a desiccant wheel with a heated effective purge angle was compared with the performance of the same wheel without a purge angle. It was found that heated effective purge angle had an overall positive effect on the performance of a rotary dehumidifier. Bourdoukan et al. [12] performed a sensitivity analysis of a desiccant wheel dehumidification using the design of experiments and also studied the effect of operating parameters on the dehumidification rate of the wheel by experimental and numerical results. Zhai et al. [13] developed a 1-D transient heat and mass transfer equations for a desiccant wheel allowing lumped formulation. The performance model related the wheel’s design parameters (wheel dimension, channel size and desiccant properties) and operating parameters (rotary speed, condition of process and regeneration air and regeneration air flow rate) to its operating performance. They also discussed the effect of some practical issues such as wheel purge, residual water in the desiccant and the wheel supporting structure on the wheel performance. Ruivo et al. [14] developed 1D transient heat and mass transfer model for desiccant wheel and presented two approaches. In the first approach, the model was valid for thickness lower than 0.1 mm, neglecting the transversal heat and mass transfer resistance in micro porous desiccant while in the second approach, the model was valid for thickness lower than 5 mm, neglecting only thermal resistance. Chung and Lee [15] developed a 1D transient model to examine the operating and design parameters (rotation speed and area ratio of regeneration to adsorption) of desiccant wheel for a range of regeneration temperature (50–150 °C). Performance evaluation was based on MRC (moisture removal capacity). Simulations were focused on the effect of desiccant isotherm at optimal conditions of the operating and design parameters and also the effect of outdoor air temperature and humidity on the optimum design parameters were examined. Antonellis et al. [16] developed a 1-D transient gas side resistance model for desiccant wheel which considered developing temperature and velocity profiles along the channels. This model was used to optimize the influence of working conditions, revolution speed and desiccant wheel configuration on the performance of the desiccant wheel. Ge et al. [17] developed a 1-D transient model to predict the performance of a compound desiccant wheel considering both the gas side resistance and the solid side resistance. The compound desiccant wheel was found to have a better performance in a climate with moderate temperatures or in a climate with a high humidity ratio. Narayanan et al. [18] developed a 1D transient gas and solid side resistance model and compared the performance of different desiccant wheel designs (Parallel flow, counter flow and additional axial cooling). They found counter flow desiccant wheel had much better dehumidification performance than parallel flow and a counter flow with axial cooling improved the dehumidification performance considerably. Yadav and Bajpai [19] presented 1D both gas and solid side resistance model to optimize the design parameters (wheel length, channel height, channel pitch, porosity and volume ratio of desiccant wheel) by taking Nusselt number and Sherwood number same. Yadav and Bajpai [20] presented 1D both gas and solid side resistance model to analyze the performance of two sectors with heated and cooled purge at different regeneration temperature and found that the desiccant system with a higher purge angle and lower regeneration angle performs better at low rph as compared to a lower purge angle and higher regeneration angle.

Many of the existing evaluations of a desiccant wheel are based on various operating parameters and design parameters. Though some researchers focused on a desiccant wheel with the purge sector but none focused on the analysis effective and ordinary regeneration sector so far. The objective of this paper is to use a mathematical model for comparing the performance of desiccant wheel with effective and ordinary regeneration sector.

2 Mathematical model

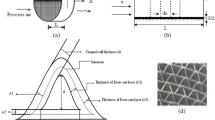
A desiccant wheel is an air to air heat and mass exchanger, with a relatively low rotational speed (N). The wheel consists of a matrix having layers of desiccant material and matrix material (supporting material). The channels can be of various shapes such as sinusoidal, honeycomb, triangular etc. The desiccant wheel is divided into three sectors according to the air streams passed. In the angular sector of process air, dehumidification of air takes place and in the angular sector of regeneration air of the wheel, humidification of the air takes place. There is another angular sector known as purge sector in which the dehumidification of air takes place and this dehumidified air becomes an input to the angular sector of regeneration. The sector angles of process air, regeneration air and purge air are denoted by ‘θp’,’ θr’ and ‘θpurge’ respectively. The rotation of the wheel causes periodic reactivation of the adsorption area. The schematic Figures of a desiccant wheel and control volume adopted in the model are shown in Fig. 1. One sinusoidal channel with a length ‘dx’ is selected as a differential control volume. It should be noted that matrix material and the desiccant material layer are shared by two channels. Where ‘A f ’ represents cross-sectional area of flow passage of one channel, ‘P e ’ is the perimeter of the air flow passage and ‘A t ’ represents the total cross-sectional area of one channel.

Fig. 1
figure 1

a Schematic diagrams of rotary desiccant wheel with effective regenerative sector. b Schematic diagrams of rotary desiccant wheel with ordinary regenerative sector. b Schematic diagrams front view of desiccant. c Schematic diagrams of differential control volume. d Schematic diagrams of cross section of channel

Full size image

The diagram of single channel is shown in Fig. 1c.

Let,

  • The height of flow passage of one channel = 2a.

  • The pitch of flow passage of one channel = 2b.

  • The cross-sectional area of flow passage of one channel, Af = 2ab.

  • Thickness of the channel wall = δ.

  • Total cross sectional area of one channel, \({\text{A}}_{\text{t}} = \frac{1}{2} \times (2{\text{a}} + {\updelta})(2{\text{b}} + {\updelta}).\)

  • The perimeter and hydraulic diameter is given by [7].

  • Perimeter of flow passage of one channel, \(\text{P}_{\text{e}} { \approx 2b + 2}\sqrt {\text{b}^{\text{2}} { + (a\uppi )}^{\text{2}} } \text{ }\frac{{\text{3 + }\left( {\frac{{\text{2b}}}{{{a\uppi }}}} \right)^{\text{2}} }}{{\text{4 + }\left( {\frac{{\text{2b}}}{{{a\uppi }}}} \right)^{\text{2}} }}.\)

  • Hydraulic diameter of flow passage of one channel, \({\rm{D}}_{\rm{h}} =\frac{{\rm{4A}_{\rm{f}}}}{{\rm{P}_{\rm{e}}}}.\).

2.1 Model assumptions

The following assumptions have been considered:

  • All air channels are assumed to be adiabatic.

  • Rotary speed is constant and low enough to neglect the effect of centrifugal force.

  • Axial heat conduction and mass diffusion in the moist air are negligible.

  • No leakage between different regions.

  • All channels in the desiccant wheel are made of the same material and configuration. There is a uniform distribution of matrix material and desiccant material along the channel.

  • The matrix material does not adsorb any moisture.

  • The inlet air conditions are uniform through the channel air domain, but may vary with time.

  • The thermodynamic properties of the dry air and the properties of the dry desiccant material as well as of the matrix material are constant.

2.2 Governing equation

In the mathematical model, the used equations are taken from Ge et al. [17]. These equations are derived from the fundamental laws of heat and mass transfer. There are two control volumes in the channel, one for moist air and the another for the layer of desiccant material.

Taking conservation of moisture and heat, four governing equations derived for moist air and desiccant material are as follows:

Mass balance of water vapour in moist air:

$$\uprho_{\text{a}} {\text{A}}_{\text{t}} {\text{A}}_{\text{r}} \left( {\frac{{\partial {\text{Y}}_{\text{a}} }}{{\partial {\text{t}}}} + {\text{u}}\frac{{\partial {\text{Y}}_{\text{a}} }}{{\partial {\text{x}}}}} \right) = {\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{d}} - {\text{Y}}_{\text{a}} } \right)$$
(1)

The first term of the left hand side \(\uprho_{\text{a}} {\text{A}}_{\text{t}} {\text{A}}_{\text{r}} \left( {\frac{{\partial {\text{Y}}_{\text{a}} }}{{\partial {\text{t}}}}} \right)\) represents the moisture storage in the air and the second term \(\uprho_{\text{a}} {\text{A}}_{\text{t}} {\text{A}}_{\text{r}} \left( {{\text{u}}\frac{{\partial {\text{Y}}_{\text{a}} }}{{\partial {\text{x}}}}} \right)\) represents the change of moisture content in control volume (dx) of air. The term of the right hand side \({\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{d}} - {\text{Y}}_{\text{a}} } \right)\) represents the convective mass transfer.

Energy balance in moist air:

$$\uprho_{\text{a}} \left( {{\text{c}}_{\text{pa}} + {\text{Y}}_{\text{a}} {\text{c}}_{\text{pv}} } \right)\left( {{\text{A}}_{\text{t}} {\text{A}}_{\text{r}} } \right)\left( {\frac{{\partial {\text{T}}_{\text{a}} }}{{\partial {\text{t}}}} + {\text{u}}\frac{{\partial {\text{T}}_{\text{a}} }}{{\partial {\text{x}}}}} \right) = {\text{hP}}_{\text{e}} \left( {{\text{T}}_{\text{d}} - {\text{T}}_{\text{a}} } \right) - {\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{d}} - {\text{Y}}_{\text{a}} } \right){\text{c}}_{\text{pv}} \left( {{\text{T}}_{\text{d}} - {\text{T}}_{\text{a}} } \right)$$
(2)

The first term of the left hand side \(\uprho_{\text{a}} \left( {{\text{c}}_{\text{pa}} + {\text{Y}}_{\text{a}} {\text{c}}_{\text{pv}} } \right)\left( {{\text{A}}_{\text{t}} {\text{A}}_{\text{r}} } \right)\left( {\frac{{\partial {\text{T}}_{\text{a}} }}{{\partial {\text{t}}}}} \right)\) represents the energy storage in the air and the second term \(\uprho_{\text{a}} \left( {{\text{c}}_{\text{pa}} + {\text{Y}}_{\text{a}} {\text{c}}_{\text{pv}} } \right)\left( {{\text{A}}_{\text{t}} {\text{A}}_{\text{r}} } \right)\left( {{\text{u}}\frac{{\partial {\text{T}}_{\text{a}} }}{{\partial {\text{x}}}}} \right)\) represents the rate of energy variation in control volume of air. The first term of the right hand side \({\text{hP}}_{\text{e}} \left( {{\text{T}}_{\text{d}} - {\text{T}}_{\text{a}} } \right)\) represents the heat transfer due to convection and the second term \({\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{d}} - {\text{Y}}_{\text{a}} } \right){\text{c}}_{\text{pv}} \left( {{\text{T}}_{\text{d}} - {\text{T}}_{\text{a}} } \right)\) represents the sensible heat transfer between air and desiccant.

Mass balance of water in the desiccant material:

$$\begin{aligned} & \uprho_{\text{a}} \in \left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}} \frac{{\partial {\text{Y}}_{\text{d}} }}{{\partial {\text{t}}}} + \uprho_{\text{d}} \left( {1 - {\epsilon} } \right)\left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}}\upphi\frac{{\partial {\text{W}}}}{{\partial {\text{t}}}} = \uprho_{\text{a}} \in \left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}} {\text{D}}_{\text{comb}} \frac{{\partial^{2} {\text{Y}}_{\text{d}} }}{{\partial {\text{x}}^{2} }} \\ & \quad + \uprho_{\text{d}} \left( {1 - {\epsilon} } \right)\left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}}\upphi{\text{D}}_{\text{S}} \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{x}}^{2} }} + {\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}} } \right) \\ \end{aligned}$$
(3)

The first term of the left hand side \(\uprho_{\text{a}} {\epsilon} \left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}} \frac{{\partial {\text{Y}}_{\text{d}} }}{{\partial {\text{t}}}}\) represents the moisture storage term inside the desiccant pore and the second term \(\uprho_{\text{d}} \left( {1 - {\epsilon} } \right)\left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}}\upphi\frac{{\partial {\text{W}}}}{{\partial {\text{t}}}}\) represents the moisture storage on the desiccant surface. The first term of the right hand side \(\uprho_{\text{a}} {\epsilon} \left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}} {\text{D}}\frac{{\partial^{2} {\text{Y}}_{\text{d}} }}{{\partial {\text{x}}^{2} }}\) represents the mass diffusion in the pores due to ordinary and Knudsen diffusion and the second term \(\uprho_{\text{d}} \left( {1 - {\epsilon} } \right)\left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}}\upphi{\text{D}}_{\text{S}} \frac{{\partial^{2} {\text{W}}}}{{\partial {\text{x}}^{2} }}\) represents the surface diffusion in an axial direction. The last term of the right hand side \({\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}} } \right)\) represents the convective mass transfer.

Energy balance in the desiccant material:

$$\begin{aligned} & {\uprho}_{\text{m}} {\text{c}}_{\text{m}} \left({1 - {{{\epsilon}}}} \right)\left({1 - {\text{A}}_{\text{r}}} \right){\text{A}}_{\text{t}} \left({1 -\upphi} \right)\frac{{\partial {\text{T}}_{\text{d}}}}{{\partial {\text{t}}}} + {{\uprho}}_{\text{d}} {\text{c}}_{\text{d}} \left({1 - {{{\epsilon}}}} \right)\left({1 - {\text{A}}_{\text{r}}} \right){\text{A}}_{\text{t}}\upphi\left[{\frac{{\partial {\text{T}}_{\text{d}}}}{{\partial {\text{t}}}} - \frac{{{\text{k}}_{\text{d}}}}{{{{\uprho}}_{\text{d}} {\text{c}}_{\text{d}}}}\frac{{\partial^{2} {\text{T}}_{\text{d}}}}{{\partial {\text{x}}^{2}}}} \right] \\ & \quad = {\text{hP}}_{\text{e}} \left({{\text{T}}_{\text{a}} - {\text{T}}_{\text{d}}} \right) + {\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left({{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}}} \right) {\text{c}}_{\text{pv}} \left({{\text{T}}_{\text{a}} - {\text{T}}_{\text{d}}} \right) + {\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left({{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}}} \right){\text{q}}_{\text{ad}} \\ \end{aligned}$$
(4)

The first term of the left hand side \({{\uprho}}_{\text{m}} {\text{c}}_{\text{m}} \left({1 - {{{\epsilon}}}} \right)\left({1 - {\text{A}}_{\text{r}}} \right){\text{A}}_{\text{t}} \left({1 -\upphi} \right)\frac{{\partial {\text{T}}_{\text{d}}}}{{\partial {\text{t}}}}\) represents the energy storage terms in the matrix material and the second term \({{\uprho}}_{\text{d}} {\text{c}}_{\text{d}} \left({1 - {{{\epsilon}}}} \right)\left({1 - {\text{A}}_{\text{r}}} \right){\text{A}}_{\text{t}}\upphi\left[{\frac{{\partial {\text{T}}_{\text{d}}}}{{\partial {\text{t}}}}} \right]\) represents the energy storage term in the desiccant material and the third term \(\uprho_{\text{d}} {\text{c}}_{\text{d}} \left( {1 - {\epsilon}} \right)\left( {1 - {\text{A}}_{\text{r}} } \right){\text{A}}_{\text{t}}\upphi\left[ {\frac{{{\text{k}}_{\text{d}} }}{{\uprho_{\text{d}} {\text{c}}_{\text{d}} }}\frac{{\partial^{2} {\text{T}}_{\text{d}} }}{{\partial {\text{x}}^{2} }}} \right]\) represents the heat conduction in the desiccant material. The first term of the right hand side \({\text{hP}}_{\text{e}} \left( {{\text{T}}_{\text{d}} - {\text{T}}_{\text{e}} } \right)\). represents the heat transfer due to convection and the second term \({\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}} } \right) {\text{c}}_{\text{pv}} \left( {{\text{T}}_{\text{a}} - {\text{T}}_{\text{d}} } \right)\) represents the sensible heat transfer between air and desiccant and the last term \({\text{h}}_{\text{m}} {\text{P}}_{\text{e}} \left( {{\text{Y}}_{\text{a}} - {\text{Y}}_{\text{d}} } \right){\text{q}}_{\text{ad}}\) represents the heat of adsorption released to the desiccant layer.

2.3 Boundary and initial conditions

The inlet conditions for the air are:

For process sector

$$\begin{gathered} {\text{T}}_{\text{a}} (0, {\text{t}}) = {\text{T}}_{{{\text{p}}, {\text{inlet}}}} \hfill \\ {\text{Y}}_{\text{a}} (0, {\text{t}}) = {\text{Y}}_{{{\text{p}}, {\text{inlet}}}} \hfill \\ \end{gathered}$$

For purge sector

$$\begin{gathered} {\text{T}}_{\text{a}} (0, {\text{t}}) = {\text{T}}_{{{\text{p}}, {\text{inlet}}}} \hfill \\ {\text{Y}}_{\text{a}} (0, {\text{t}}) = {\text{Y}}_{{{\text{p}}, {\text{inlet}}}} \hfill \\ \end{gathered}$$

For ordinary regeneration sector

$$\begin{gathered} {\text{T}}_{\text{a}} ({\text{L}}_{\text{w}} , {\text{t}}) = {\text{T}}_{{{\text{r}}, {\text{inlet}}}} \hfill \\ {\text{Y}}_{\text{a}} \left( {{\text{L}}_{\text{w}} , {\text{t}}} \right) = {\text{Y}}_{{{\text{r}}, {\text{inlet}}}} \hfill \\ \end{gathered}$$

For effective regeneration sector

$$\begin{aligned} &{\text{T}}_{\text{a}} ({\text{L}}_{\text{w}} , {\text{t}}) = {\text{T}}_{{{\text{r}}, {\text{inlet}}}} \hfill \\ &{\text{Y}}_{\text{a}} \left( {{\text{L}}_{\text{w}} , {\text{t}}} \right) = {\text{Y}}_{{{\text{r}}, {\text{inlet}}}} = {\text{Y}}_{{{\text{purge air}}, {\text{outlet}}}} \hfill \\ \end{aligned}$$

The initial temperature and humidity ratio of the air are assumed to be uniform and also initial temperature and water content of the desiccant are assumed to be uniform:

$$\begin{gathered} {\text{T}}_{\text{a}} (x, 0) = {\text{T}}_{{{\text{a}}0}} \hfill \\ {\text{Y}}_{\text{a}} (x, 0) = {\text{Y}}_{{{\text{a}}0}} \hfill \\ {\text{T}}_{\text{d}} (x, 0) = {\text{T}}_{{{\text{d}}0}} \hfill \\ {\text{W}}(x, 0) = {\text{W}}_{0} \hfill \\ \end{gathered}$$

2.4 Auxiliary conditions

Humidity ratio and relative humidity are related as [17]

$${\text{Y}}_{\text{d}} = \frac{{0.62188{\text{P}}_{\text{v}} }}{{{\text{P}}_{\text{a}} - {\text{P}}_{\text{v}} }} = \frac{{0.62188{\text{RH}}_{\text{d}} }}{{{\raise0.7ex\hbox{${{\text{P}}_{\text{a}} }$} \!\mathord{\left/ {\vphantom {{{\text{P}}_{\text{a}} } {{\text{P}}_{\text{vs}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{P}}_{\text{vs}} }$}} - {\text{RH}}_{\text{d}} }}$$
(5)

where \(P_{vs}\) is the saturation pressure of water vapour which can be found using the following relation [17]

$${\text{P}}_{\text{vs}} = {\text{e}}^{{\left( {23.196 - \frac{3816.44}{{{\text{T}}_{\text{d}} - 46.13}}} \right)}}$$
(6)

The equilibrium isotherm is given by [23]

$${\text{RH}}_{\text{d}} = 0.0078 - 0.05759{\text{W}} + 24.16554{\text{W}}^{2} - 124.78{\text{W}}^{3} + 204.226{\text{W}}^{4}$$
(7)

The adsorption heat of regular density silica gel as recommended by [2]

$${\text{q}}_{\text{ad}} = {\text{h}}_{\text{fg}} \left( {1.0 + 0.2843{\text{e}}^{{ - 10.28{\text{W}}}} } \right)$$
(8)

The latent heat of the water vapour at a different temperature is given by [21]

$${\text{h}}_{\text{fg}} = (2504.4 - 2.4425 {\text{T}}_{\text{d}} ) \times 1000$$
(9)

The vapour can diffuse through pores of desiccant by three mechanisms, namely surface diffusion, ordinary diffusion and Knudsen diffusion with diffusion coefficient of \({\text{D}}_{\text{S}}\), \({\text{D}}_{\text{o}}\) and \({\text{D}}_{\text{k}}\). The ordinary diffusion coefficient and Knudsen diffusion coefficients are combined by combine diffusivity \({\text{D}}_{\text{comb}}\). These coefficients can be estimated by the following expressions [23].

$${\text{D}}_{\text{comb}} = \frac{1}{{{{\uptau} }}}\left( {\frac{1}{{{\text{D}}_{0} }} + \frac{1}{{{\text{D}}_{\text{k}} }}} \right)^{ - 1}$$
(10)
$${\text{D}}_{\text{S}} = \frac{{1.6 \times 10^{ - 6} }}{{{{\uptau} }}}{\text{e}}^{{\left( { - 0.974 \times 10^{ - 3} \frac{{{\text{q}}_{\text{ad}} }}{{{\text{T}}_{\text{d}} }}} \right)}}$$
(11)

where, τ is tortuosity factor that account for the increase in diffusion length due to the tortuous path of real pores and its value is 2.8 for regular density silica gel.

$${\text{D}}_{\text{o}} = 1.735 \times 10^{ - 4} \frac{{{\text{T}}_{\text{d}}^{1.685} }}{{{\text{P}}_{\text{a}} }}$$
(12)
$${\text{D}}_{\text{k}} = 97{\text{r}}\left( {\frac{{{\text{T}}_{\text{d}} }}{\text{M}}} \right)^{0.5}$$
(13)

Sutherland’s formula can be used to calculate the dynamic viscosity of an air as a function of the temperature [24].

$$\upmu = \upmu_{0} \left( {\frac{{{\text{T}}_{\text{so}} + {\text{C}}_{0} }}{{{\text{T}} + {\text{C}}_{0} }}} \right)\left( {\frac{\text{T}}{{{\text{T}}_{\text{so}} }}} \right)^{3/2}$$
(14)

Where, μ = dynamic viscosity (Pa s) at temperature \({\text{T}}\); \(\upmu_{0}\) = reference viscosity (Pa s) at reference temperature \({\text{T}}_{\text{so}}\); T = temperature of air in Kelvin; \({\text{T}}_{\text{so}}\) = reference temperature in Kelvin; \({\text{C}}_{0}\) = Sutherland’s constant for the air; \(\upmu_{0} = 18.27 \times 10^{ - 6} \, {\text{Pa s}}\); \({\text{T}}_{\text{so}}\) = 291.15 K; \({\text{C}}_{0}\) = 120 K.

The Nusselt number for the fully developed flow depends on the channel geometry is given by [16]

$${\text{Nu}}_{\text{FD}} = 1.1791 \left[ {1 + 2.7701\left( \upalpha \right) - 3.1901\left( {\upalpha} \right)^{2} + 1.9975\left( {\upalpha} \right)^{3} - 0.4966\left( {\upalpha} \right)^{4} } \right]$$
(15)

where, Aspect ratio, \({\upalpha} = \frac{{2{\text{a}}}}{{2{\text{b}}}}\)

In order to develop the temperature and velocity profile along the channel, Nusselt number is evaluated by [16]

$${\text{Nu}} = {\text{Nu}}_{\text{FD}} + \frac{0.0841}{{0.002907 + {\text{Gz}}^{ - 0.6504} }}$$
(16)
$$Re = \frac{{{\uprho \text{uD}}_{\text{h}} }}{\upmu}$$
(17)
$${ \Pr } = \frac{{{\upmu \text{c}}_{\text{p}} }}{\text{k}}$$
(18)
$${\text{Gz}} = \frac{{{{Re}}\Pr {\text{P}}_{\text{e}} }}{{4{\text{L}}_{\text{w}} }}$$
(19)

The following heat transfer coefficient is adopted

$${\text{h}} = \frac{\text{Nuk }}{{{\text{D}}_{\text{h}} }}$$
(20)

The following relations are adopted from Chilton Colburn analogy.

$${\text{Sh}} = {\text{NuLe}}^{{\left( \frac{1}{3} \right)}}$$
(21)
$${\text{Le}} = \frac{\text{k}}{{{\uprho \text{c}}_{\text{p}} {\text{D}}_{\text{m}} }}$$
(22)

The following mass transfer coefficient is adopted

$${\text{h}}_{\text{m}} = \frac{{{\uprho \text{ShD}}_{\text{m}} }}{{{\text{D}}_{\text{h}} }}$$
(23)

The mass diffusion coefficient of vapour in the air is given by [17]

$${\text{D}}_{\text{m}} = 2.302 \times 10^{ - 5} \frac{{{\text{P}}_{0} }}{\text{P}}\left( {\frac{\text{T}}{{{\text{T}}_{0} }}} \right)^{1.81}$$
(24)

where,

$$\begin{aligned} {\text{P}}_{0} &= 0.98 \times 10^{5} \, {\text{Pa}} \hfill \\ {\text{T}}_{0} &= 256 \,{\text{K}} \hfill \\ \end{aligned}$$

2.5 Solution method

In this model the four governing equations of heat and mass transfer are non-linear and coupled. The four governing equations are being solved using a PDE solver. This PDE solver is based on the finite element method (FEM). The programming is done in the script language of solver. Two programs in the script language are made for process and regeneration in two sectors of a desiccant wheel and three programs in the script language are made for process, purge sector and regeneration of a desiccant wheel. These three programs are coupled in the solver to simulate real conditions.

3 Model validation

3.1 Heat and mass transfer

Experimental results related to the desiccant wheel Kodama [22] are also adopted to validate the present model. The desiccant wheel channel pitch, height and wall thickness are 0.0032, 0.0018 and 0.0002 m respectively and the desiccant wheel length is 0.2 m operating under a wide range of operating conditions which are given in Table 1.

Table 1 Dehumidification capacity: input data used in comparison between simulation and experimental results
Full size table

Experimental data and simulation results shown in Fig. 2 agree well under the various conditions. The mathematical model is fully validated and ready for implementation for different wheel designs.

Fig. 2
figure 2

\({\text{Y}}_{{{\text{p}},{\text{out}}}} /{\text{Y}}_{{{\text{p}},{\text{in}}}}\) versus revolution speed: comparison between experimental data and simulation results for different working conditions \(({\text{u}}_{{{\text{p}},{\text{in}}}} = {\text{u}}_{{{\text{r}},{\text{in}}}} = 1\,{\text{m}}/{\text{s}}, {\text{L}}_{\text{w}} = 0.2\,{\text{m}})\)

Full size image

3.2 Pressure drop

The experimental data available for a commercial desiccant wheel verifies the pressure drop correlation where the geometry of channel is triangular (channel height = 0.002 m, channel pitch = 0.004 m and wheel length = 0.2 m) Antonellis et al. [16].

The pressure drop was calculated as Harshe et al. [7]

$$\Delta {\text{P}} = \frac{{2{{\text{f}}\uprho {\text{u}}}^{2} {\text{L}}_{\text{w}} }}{{{\text{D}}_{\text{h}} }} + \frac{{{\text{K}}_{0} {\uprho \text{u}}^{2} }}{2}$$

where f is the friction factor and \({\text{K}}_{0}\) represents the velocity head loss at the entry and exit of the desiccant wheel.

The friction factor f is given by Antonellis et al. [16].

Friction factor, \({\text{f}} = 13/{Re}\;\) \({\text{K}}_{0}\) = 0.5 = constant for sudden contraction loss.

Table 2 shows both experimental data and simulation results of pressure drop for different values of the face velocity.

Table 2 Pressure drop: comparison between simulation and experimental results
Full size table

Experimental data and simulation result closely match.

Good agreement of experimental and simulation result for pressure difference.

4 Numerical results and discussion

The performance of the desiccant wheel of the specification listed in Table 3 is analyzed under various operating and structural conditions as listed in Table 4.

Table 3 Specifications of the desiccant wheel
Full size table
Table 4 Operating and structural parameters
Full size table

4.1 Performance index

The main function of a desiccant wheel is to remove the water vapour from the process air. Therefore, the performance indices represent the dehumidification capacity of the desiccant. There are several performance indices such as moisture removal, relative moisture relative efficiency, effectiveness of wheel and DCOP (Dehumidification coefficient of performance) of wheel. Moisture removal (MR) is adopted as an index to represent the absolute dehumidification capacity of desiccant dehumidifier.

$${\text{M}}_{{\rm r}}= {\text{Y}}_{{{\text{p}},{\text{in}}}}-{\text{Y}}_{{{\text{p}},{\text{out}}}}$$

where, \({\text{Y}}_{{{\text{p}},{\text{in}}}}\) is the humidity ratio of the process air at the inlet and \({\text{Y}}_{{{\text{p}},{\text{out}}}}\) is the humidity ratio of the process air at the outlet.

4.2 Introduction of effective and ordinary regeneration sector and its effect on the performance of desiccant wheel under various operating condition

4.2.1 Theory for 3(a) and 3(b) figure

Schematic diagrams of desiccant wheel with effective and ordinary regeneration sector are shown in Fig. 3a–d.

Fig. 3
figure 3

a Schematic diagrams of desiccant wheel with effective regeneration sector, b Schematic diagrams of desiccant wheel with ordinary regeneration sector. c Schematic diagrams of desiccant wheel configuration with effective regeneration sector. d Schematic diagrams of desiccant wheel configuration with ordinary regeneration sector

Full size image

4.2.2 Performance comparison of desiccant wheel with effective and ordinary regeneration sector at different rotational speeds

Figure 4 shows that moisture removal initially increases and then becomes steady for both effective and ordinary regeneration sector with the increase in rotational speed of desiccant wheel. For all the ranges of speed of rotation, moisture removal of process air with effective regeneration sector is better as compared with ordinary regeneration sector because in case of effective regeneration sector output of purge sector is the input of regeneration sector due to which humidity ratio at the inlet of regeneration decreases. Hence performance of process sector increases. At low speed of rotation, effect of regeneration sector is less and it increases with increase in rotational speed of desiccant wheel; for example at rotational speed of 10 rph and 60 rph the difference in moisture removal between effective and ordinary regeneration sector is 0.000891 and 0.001665 respectively. Maximum value of moisture removal for effective regeneration sector is 0.006104 at 40 rph and maximum value of moisture removal for ordinary regeneration sector is 0.00443 at 35 rph.

Fig. 4
figure 4

Variation of moisture removal with rotation of desiccant wheel with effective and ordinary regeneration sector

Full size image

Figure 5 shows that with an increase in rotational speed of desiccant wheel, the temperature difference of process air initially increases and then becomes steady for both effective and ordinary regeneration sector. For all the range of speed of rotation, the temperature difference of process air with effective regeneration sector is greater as compared with ordinary regeneration sector. At low speed of rotation, effect of regeneration sector is less and it increases with increase in rotational speed of desiccant wheel; for example at rotational speed of 10 and 60 rph, the temperature difference of process air between effective and ordinary regeneration sector is 1.61 °C and 3.2 °C respectively. Maximum value of temperature difference of process air with effective regeneration sector is 11.22 °C at 40 rph and maximum value of temperature difference of process air with ordinary regeneration sector is 8.02 °C at 35 rph.

Fig. 5
figure 5

Variation of temperature with rotation of desiccant wheel with effective and ordinary regeneration sector

Full size image

4.2.3 Performance comparison of desiccant wheel with effective and ordinary regeneration sector at different regeneration temperatures

Figure 6 shows that moisture removal increases for both effective and ordinary regeneration sector with increase in the regeneration temperature. Maximum value of moisture removal for effective and ordinary regeneration sector is 0.006048 and 0.006019 respectively, at a regeneration temperature of 373 °C. But difference in moisture removal between effective and ordinary regeneration sector is small, which means an increase in regeneration temperature does not affect moisture removal to a great extent.

Fig. 6
figure 6

Variation of moisture removal with regeneration temperature with effective and ordinary regenerative sector

Full size image

Figure 7 shows that temperature difference of process air increases for both effective and ordinary regeneration sector with increase in the regeneration temperature. Maximum value of temperature difference of process air for effective and ordinary regeneration sector is 11.08 and 11.02 °C respectively, at a regeneration temperature of 373 °C. But difference in temperature between effective and ordinary regeneration sector is small, it means increase in regeneration temperature does not affect temperature difference to a great extent.

Fig. 7
figure 7

Variation of temperature with regeneration temperature with effective and ordinary regeneration sector

Full size image

4.2.4 Performance comparison of desiccant wheel with effective and ordinary regeneration sector at different velocities

Figure 8 shows that moisture removal initially increases and then decreases for both effective and ordinary regeneration sector with the increase in velocity. At low velocity, difference of moisture removal of process air between effective and ordinary regeneration sector is small. As velocity increases difference of moisture removal is maximum and it is maximum at optimum velocity of 2 m/s. Maximum value of moisture removal for both effective and ordinary regeneration sector is 0.004506 and 0.004375 respectively, at a velocity of 2 m/s.

Fig. 8
figure 8

Variation of moisture removal with velocity with effective and ordinary regeneration sector

Full size image

Figure 9 shows that with the increase in velocity, temperature difference of process air initially increases and then decreases for both effective and ordinary regeneration sector. At low velocity, difference of temperature of process air between effective and ordinary regeneration sector is small, as velocity increases, temperature difference is maximum and it is maximum at optimum velocity of 2 m/s. Maximum value of temperature difference for effective and ordinary regeneration sector is 8.15 and 7.91 °C respectively, at a velocity of 2 m/s.

Fig. 9
figure 9

Variation of temperature difference with velocity with effective and ordinary regeneration sector

Full size image

4.2.5 Performance comparison of desiccant wheel with effective and ordinary regeneration sector at different ambient moisture

Figure 10 shows that moisture removal increases for both effective and ordinary regeneration sector with increase in the ambient moisture. As the ambient moisture increases, difference of moisture removal of process air between effective and ordinary regeneration sector remains same. Maximum value of moisture removal for effective and ordinary regeneration sector is 0.004859 and 0.004792 respectively at ambient moisture of 0.0025 kgwater vapour/kgdry air.

Fig. 10
figure 10

Variation of moisture removal with ambient moisture with effective and ordinary regeneration sector

Full size image

Figure 11 shows that with an increase in the ambient moisture, the temperature difference of process air increases for both effective and ordinary regeneration sector. As the ambient moisture increases, difference of temperature of process air between effective and ordinary regeneration sector is same. Maximum value of temperature difference of process air for effective and ordinary regeneration sector is 8.77 and 8.65 °C, at ambient moisture of 0.0025 kgwater vapour/kgdry air.

Fig. 11
figure 11

Variation of temperature difference with ambient moisture with effective and ordinary regeneration sector

Full size image

5 Conclusion

The main conclusions of this paper are summarized as

  1. 1.

    For all the given rotational speeds of desiccant wheel, the moisture removal for effective regeneration sector is better as compared with ordinary regeneration sector. At low speed of rotation, effect of effective regeneration sector is less and it increases with increase in rotational speed of desiccant wheel.

  2. 2.

    At any regeneration temperature, the moisture removal is slightly better for effective regeneration sector as compared with ordinary regeneration sector.

  3. 3.

    At any velocity between 1 and 4 m/s, the moisture removal for effective regeneration sector is better as compared with ordinary regeneration sector and maximum difference of moisture removal for effective and ordinary regeneration sector is 0.000131 at 2 m/s.

  4. 4.

    At any ambient moisture, the moisture removal is slightly better for effective regeneration sector as compared with ordinary regeneration sector.