Entropy minimization in micro-scale evaporating thin liquid film in capillary tubes

Abstract

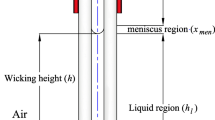
An analysis has been provided for the entropy generated for the micro/nano scale heat and mass transfer in a capillary tube in terms of the gradients of velocity, temperature and concentration as well as the physical properties of the fluid. The heat and mass transfer rates are assumed to be uniform on the surface of the capillary tube. The optimum tube diameter that corresponds to the minimization of entropy generated and minimization of fluid flow resistance is about 1 mm. We have applied the method of thermodynamic optimization to capillary driven systems. The objective was to identify the geometric configuration that maximized performance by minimizing the entropy generated when the flow rate is prescribed.

Appendix

The general formulation for the local entropy generation per unit volume g, in an incompressible Newtonian fluid had been derived by Hirschfelder et al. [24], and is given as

$$ S^{\prime\prime\prime} = \frac{{\mu ^{\prime}}}{T}\left( {\frac{{\partial U_{\text{i}} }}{{\partial x_{\text{j}} }}} \right)\left[ {\frac{{\partial U_{\text{i}} }}{{\partial x_{\text{j}} }} + \frac{{\partial U_{\text{j}} }}{{\partial x_{\text{i}} }}} \right] - \frac{1}{T}\left[ {\sum\limits_\alpha {J_{\alpha {\text{i}}} \left( {\frac{{\partial \mu _\alpha }}{{\partial x_{\text{i}} }}} \right) + \frac{{\varepsilon _{\text{i}} }}{T}\left( {\frac{{\partial T}}{{\partial x_{\text{i}} }}} \right)} + \sum\limits_\alpha {\bar S_\alpha J_{\alpha {\text{i}}} \left( {\frac{{\partial T}}{{\partial x_{\text{i}} }}} \right) - \sum\limits_\alpha {J_{\alpha {\text{i}}} X_{\alpha {\text{i}}} + \sum\limits_\alpha {\bar K_\alpha \mu _\alpha } } } } \right] $$

(20)

where the first term is due to fluid friction and the second and third terms are due to mass diffusion and heat conduction. The fourth term arises from the coupling between heat and mass transfer, the fifth term is due to body forces, and the sixth term represents the effect due to chemical reactions.

Consider flow in a tube with heat transfer occurring at both walls. The chemical reactions and gravitational effects are neglected, and the fluid is considered to be a binary mixture of two ideal gases with species A diffusing perpendicular to the flow direction.

The chemical potential of species A can be expressed in the following form [25]:

$$ \mu _A \left( {T,P_A } \right) = \mu _A^0 \left( T \right) + RT\ln \left( {P_A/P_0 } \right) $$

(21)

where P _A is the partial pressure of species A, and μ ⁰ _A is the standard state chemical potential of pure species A at temperature T. If c_p,A is constant, μ ⁰ _A (T) can be expressed as

$$ \mu _A^0 (T) = c_{p,A} \left( {T - T_0 } \right) - c_{p,A} T\ln \left( {\frac{T}{{T_0 }}} \right) + h_{A0} - Ts_{A0} $$

(22)

where P ₀ and T ₀ are the reference pressure and temperature, and h _A0 and s _A0 are the enthalpy and entropy of the diffusing species A, at T ₀ and P ₀.

Using Eqs. (21) and (22), the partial molar entropy of species A, $\bar S_A,$ can be simplified as

$$ \bar S_A \equiv - \left( {\frac{{\partial \mu _A }}{{\partial T}}} \right)_{p,n_{j \ne A} } = - R\left( {\ln \frac{{C_A }}{{C_0 }}} \right) + c_{v,A} \left( {\ln \frac{T}{{T_0 }}} \right) + s_{A0} $$

(23)

where C ₀ is the reference mass concentration at T ₀ and P ₀.

Substituting Eqs. (21)–(23) into Eq. (20), the local entropy generation g, in a tube flow with single species A, diffusing in the y-direction can be expressed as:

$$ S^{\prime\prime\prime} = \mathop {\frac{{\mu ^{\prime}}}{T_0}\left\{ {\left( {\frac{{\partial u}}{{\partial y}}} \right)^2 } \right\}}\limits^{( 1)} + \mathop {R\left( {\frac{{D_{v,A} }}{{C_A }}} \right)\left( {\frac{{{\text{d}}C_A }}{{{\text{d}}y}}} \right)^2 }\limits^{( 2)} + \mathop {\frac{k}{{{T_0}^2 }}\left[ {\left( {\frac{{\partial T}}{{\partial x}}} \right)^2 + \left( {\frac{{\partial T}}{{\partial y}}} \right)^2 } \right]}\limits^{( 3)} + \mathop {R\left( {\frac{{D_{v,A} }}{T_0}} \right)\left( {\frac{{{\text{d}}C_A }}{{{\text{d}}y}}} \right)\left( {\frac{{\partial T}}{{\partial y}}} \right)}\limits^{( 4)} $$

(24)

where term (1) is due to fluid friction, term (2) due to mass diffusion, term (3) due to the flux of heat, and term (4) due to the coupling effect between heat and mass transfer.