Skip to main content
SpringerLink
Log in

Numerical investigation of transpiration and ablation cooling

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

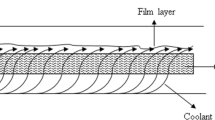
Abstract

To predict the integral performance of transpiration and ablation cooling during the reentry of hypersonic vehicles, an unsteady numerical model based on the assumption of thermal equilibrium is presented. The non-thermal equilibrium model and the thermal equilibrium model are coupled by the effective thermal properties of the porous matrix and the coolant. The calculation using the thermal equilibrium model shows the influence of the variation of the effective thermal properties on the numerical results by a comparison between constant and variable thermal properties. The comparison indicates that near the melting temperature of the porous matrix, the position of the moving boundary due to ablation is sensitive to the temperature, therefore, the variation of the thermal properties are considered in this paper. The process of ablation and transpiration cooling is simulated under different numerical conditions. The simulations demonstrate that the injection rate of coolant mass flow and initial temperature of cooling are important parameters for the control of the ablation process.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

c :

Specific heat capacity [J/(kgK)]

d p :

Mean diameter of pore (m)

k :

Thermal conductivity [W/(mK)]

l :

Initial thickness of porous plate (m)

h s :

Interfacial heat transfer coefficient [W/(m2K)]

h v :

Volumetric heat transfer coefficient [W/(m3K)]

S :

Thickness (m)

T :

Temperature (K)

t :

Time (s)

v :

Velocity (m/s)

y :

Coordinate

Q 0 :

Heat flux (W/m2)

\(\dot{m}_{\rm c}\) :

Coolant mass flow rate [kg/(m2s)]

\(\vec{V}\) :

Velocity vector (m/s)

α:

Thermal diffusivity (m2/s)

β:

Thermal polarizability

ɛ:

Porosity

ρ:

Density (kg/m2)

λ:

Latent heat of the solid matrix (J/kg)

0:

Initial time

c:

Constant/coolant

e:

Effective

m:

Ablation

p:

Porous material

References

  1. Agapiou JS, de Vries MF (1989) An Experimental determination of the thermal conductivity of a 304L Stainless steel powder metallurgy material. ASME J Heat Transfer 111:281–292

    Article  Google Scholar 

  2. Alazmi B, Vafai K (2000) analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Int J Heat Mass Transfer 44:1735–1749

    Article  Google Scholar 

  3. Alazmi B, Vafai K (2002) Constant wall heat flux boundary conditions in porous media under local thermal non-equilibrium conditions. Int J Heat Mass Transfer 45:3071–3087

    Article  MATH  Google Scholar 

  4. Amiri A, Vafai K (1994) Analyses of dispersion effects and non-thermal equilibrium, non- darcian, variable porous incompressible flow through porous media. Int J Heat and Mass Transfer 37:939–954

    Article  Google Scholar 

  5. Argento C, Bouvard D (1996) Modeling the effective thermal conductivity of random packing of spheres through densification. Int J Heat Mass Transfer 39:1343–1350

    Article  MATH  Google Scholar 

  6. Bauer TH (1993) A general analytical approach toward the thermal conductivity of porous media. Int J Heat Mass Transfer 36:4181–4191

    Article  MATH  Google Scholar 

  7. Choi SH, Scotti SJ, Song KD, Reis H (1997) Transpiration cooling of a scram jet engine combustion chamber. In: The 32th AIAA thermophysics conference, Atlanta, Georgia, AIAA 97–2576

  8. Crank J (1984) Free and moving boundary problems. Clarendon Press, Oxford

    MATH  Google Scholar 

  9. Garayev KG (1999) Optimal injection of coolant into the laminar boundary layer of a compressible gas. J Appl Math Mech 65(2):253–259

    Article  Google Scholar 

  10. Glass DE, Dilley AD (1999) Numerical analysis of convection/transpiration cooling, NASA/TM-1999–209828

  11. Gonzo EE (2002) Estimating correlations for the effective thermal conductivity of granular materials. Chem Eng J 90:299–302

    Article  Google Scholar 

  12. Jeng TM, Wang MP, Hwang GJ, Hung YH (2004) A new semi-empirical model for predicting heat transfer characteristics in porous channels. Exp Ther Fluid Sci 29:9–21

    Article  Google Scholar 

  13. Jiang P, Ren ZP, Wang BX (1999) Numerical simulation of forced convection heat transfer in porous plate channels using thermal equilibrium and nonthermal equilibrium models. Numerical Heat Transfer Part A 35:99–113

    Article  Google Scholar 

  14. Khosla PK, Rubin SG (1974) A diagonally dominant second order accurate implicit scheme. Comput Fluid 2:207–209

    Article  MATH  Google Scholar 

  15. Krupiczka R (1967) Analysis of thermal conductivity in granular materials. Int Chem Eng 7:122–144

    Google Scholar 

  16. Kuwahara F, Shirota M, Nakayama A (2001) A numerical study of interfacial convective heat transfer coefficient in two-energy equation model for convection in porous media. Int J Heat Mass Transfer 44:1153–1159

    Article  MATH  Google Scholar 

  17. Lee D, Vafai K (1999) Analytical characterization and conceptual assessment of solid and fluid temperature differentials in porous media. Int J Heat Mass Transfer 42:423–435

    Article  MATH  Google Scholar 

  18. Minkowycz WJ, Haji-Sheikh A, Vafai K (1999) on departure from local thermal equilibrium in porous media due to a rapidly changing heat source: the Sparrow number. Int J Heat Mass Transfer 42:3373–3385

    Article  MATH  Google Scholar 

  19. Mori S, Kumita M, Takahashi T, Tanimoto A, Sakakibara M (1997) Heat and mass transfer from a flat plate of finite thickness to a boundary layer flow with transpiration. Energy Convers Manage 38(10–13):1209–1218

    Article  Google Scholar 

  20. Nield DA (2002) A note on the modeling of local thermal non-equilibrium in structured porous medium. Int J Heat Mass Transfer 45:4367–4368

    Article  MATH  Google Scholar 

  21. Nield DA, Bejan A (1999) Convection in Porous Media, 2nd edn. Springer, Berlin Heidelberg New York, p 26

    MATH  Google Scholar 

  22. Oezisik MN (1993) Heat conduction, 2nd edn. Wiley, New York, pp 392–433

    Google Scholar 

  23. Perry RH, Chilton CH (1984) Chemical engineers’ handbook, 6th edn. McGraw-Hill, New York

    Google Scholar 

  24. Polezhaev YV, Seliverstov EM (2002) A universal model of heat transfer in systems with penetration cooling. High Temp 40:856–864

    Article  Google Scholar 

  25. Schumann TEW (1929) Heat transfer: a liquid flowing through a porous prism. J Franklin Inst 208:405–416

    Article  MATH  Google Scholar 

  26. Stefan J (1889) Ueber die Theorie der Eisbildung, insbesondere ueber die Eisbildung im Polarmeere, Wien. Akad Mat Nat 98(11a):965–983

    Google Scholar 

  27. Tavman IH (1996) Effective thermal conductivity of granular porous materials. Int Commun Heat Mass Transfer 23:169–176

    Article  Google Scholar 

  28. Tien CL, Vafai K (1990) Convective and radiative heat transfer in porous media. Adv Appl Mech 27:225–281

    MATH  Google Scholar 

  29. Trevino C, Medina A (1999) Analysis of transpiration cooling of a thin porous plate in a hot laminar convective flow. Eur J Mech B Fluids 18(2):227–243

    Article  Google Scholar 

  30. Vargaftik NB (1975) Tables of thermophysical properties of liquids and gases, 2nd edn. Hemisphere Publishing Corportion, Washington

    Google Scholar 

  31. Zhang Y, Faghri A (1999) Melting of a subcooled mixed powder bed with constant heat flux heating. Int J Heat Mass Transfer 42:775–788

    Article  MATH  Google Scholar 

  32. Tan Z, Guo G (1994) Thermal property of engineering alloy (in Chinese). Metallurgy Publisher, Beijing

    Google Scholar 

Download references

Acknowledgements

The project is supported by National Natural Science Foundation of China (No. 90305006) and Educational Administration Foundation of Anhui Province (No. 2004kj365zd). One of the authors (Jianhua Wang) is also grateful for the financial support provided by the Foundation of the Education Ministry of China for the Returned Overseas Scholars. We also thank Prof. Casey and Dr. Messner at the Institute of Thermal Fluid- Machinery and Laboratory of University Stuttgart for their helpful guidance and support. The first figure of this paper is taken from the paper of Choi et al. [7], we would like to express our appreciation to the authors.

Author information

Authors and Affiliations

  1. 13th Department, University of Science and Technology of China, Jinzhai Road 96, Hefei, 230026, People’s Republic of China

    Jianhua Wang & Xingsi Han

Authors
  1. Jianhua Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xingsi Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jianhua Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, J., Han, X. Numerical investigation of transpiration and ablation cooling. Heat Mass Transfer 43, 275–284 (2007). https://doi.org/10.1007/s00231-005-0073-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-005-0073-7

Keywords

Search

Navigation