Skip to main content
SpringerLink
Log in

Buoyancy effects on mixed convection heat and mass transfer in a duct with sudden expansions

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

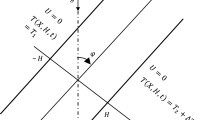
Abstract

The present paper deals with the study of heat and mass transfer by mixed convection in an inclined duct preceded with a double step expansion. The control volume based finite element method was used to solve the set of non-dimensional equations for the vorticity, stream function, energy and species conservation. Numerical simulations are carried out for different combinations of the Lewis number, thermal and mass diffusion Grashof numbers for different inclinations. Streamlines, temperature and concentration distributions are presented and discussed. The results show the effect of the secondary flow induced by buoyancy forces and the presence of the double step expansion on the heat and mass transfer mechanism. It is found that the recirculation vortices induced by the expansion can be present along the channel and the flow structure can be wavy. For the vertical orientation, asymmetric fields are observed for the different simulated cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Abbreviations

C :

Concentration

\(\tilde C\) :

Dimensionless concentration \(\tilde C = (C - C_0 )/(C_{\text{1}} - C_0 )\)

C 0 :

Concentration of inlet air

C 1 :

Concentration of the wall

D :

Thermal diffusivity

g :

Gravitational acceleration

Grt:

Thermal Grashof number Grt=βtg(T1−T0)w 31 /ν2

Grs:

Solutal Grashof number Grs=βsg(C1−C0)w 31 /ν2

N :

Buoyancy ratio, N = Grs/Grt

N 1 :

Geometrical number N1=w1/w2

N 2 :

Geometrical number N2=w1/L

L :

Channel length

Le:

Lewis number Le=α/D

Pr:

Prandtl number Pr=ν/α

Qt:

Wall heat flux \({\text{Qt}} = \partial \tilde T/\partial \tilde y\)

Qc:

Wall mass flux \({\text{Qc}} = \partial \tilde C/\partial \tilde y\)

Re:

Reynolds number Re=U0w1/ν

t :

Time

\({\tilde t}\) :

Dimensionless time \(\tilde t = t\,U_0 /w_1 \)

T :

Temperature

\( \tilde{T} \) :

Dimensionless temperature \(\tilde T = (T - T_0 )/(T_1 - T_0 )\)

T 0 :

Temperature of inlet air

T 1 :

Temperature of the wall

U 0 :

Center line velocity at the inlet

u, v:

Velocity components in x and y direction

\(\tilde u,\tilde v\) :

Dimensionless velocity components in x and y directions \(\tilde u = u/U_0 ,\tilde v = v/U_0 \)

w 1 :

Upstream channel height

w 2 :

Downstream channel height

x, y:

Cartesian coordinates

\(\tilde x,\tilde y\) :

Dimensionless Cartesian coordinates \(\tilde x = x/w_1 ,\tilde y = y/w_1 \)

α:

Thermal diffusivity

βt:

Thermal expansion coefficient

βs:

Solutal expansion coefficient

γ:

Inclination angle as measured from the vertical axis

ν:

Kinetic viscosity

ω:

Vorticity

\({\tilde \omega }\) :

Dimensionless vorticity \(\tilde \omega = \omega w_1 /U_0 \)

ψ:

Stream function

\({\tilde \psi }\) :

Dimensionless stream function \(\tilde \psi = \psi /(w_1 U_0 )\)

References

  1. Kakac S, Shah RK, Aung W (1987) Handbook of single-phase convective heat transfer. Wiley, New York, pp 3–14

    Google Scholar 

  2. Choi CY, Ortega A (1993) Mixed convection in an inclined channel with a discrete heat source. Int J Heat Mass Transfer 36(12):3119–3134

    Article  CAS  Google Scholar 

  3. Raji A, Hasnaoui M, Zrikem Z (1995) Convection mixte dans un canal incliné de longueur finie contenant des obstacles et chauffé de manière isotherme et discrète. Rev Gén Thermique 34(399):202–209

    Google Scholar 

  4. Durst F, Pereira JCF, Tropera C (1993) The plane symmetric sudden-expansion flow at low Reynolds numbers. J Fluid Mech 248:567–581

    CAS  Google Scholar 

  5. Armaly AF, Durst F, Pereira JCF, Schonung B (1983) Experimental and theoretical investigation of backward-facing step flow. J Fluid Mech 127:473–496

    Google Scholar 

  6. Hong B, Armaly BF, Chen TS (1993) Laminar mixed convection in a duct with a backward-facing step: the effects of inclination angle and Prandtl number. Int J Heat and Mass Transfer 36(12):3059–3067

    Article  CAS  Google Scholar 

  7. Lin JT, Armaly BF, Chen TS (1991) Mixed convection heat transfer in inclined backward-facing step flows. Int J Heat Mass Transfer 34(6):1568–1571

    Article  Google Scholar 

  8. Cherdron W, Durst F, Whitelaw JH (1978) Asymmetric flows and instabilities in symmetric ducts with sudden expansions. J Fluid Mech 84(1):13–31

    CAS  Google Scholar 

  9. Abu-Mulaweh HI, Armaly BF, Chen TS (1993) Measurement of laminar mixed convection in boundary-layer flow over horizontal and inclined backward-facing steps. Int J Heat Mass Transfer 36(7):1883–1895

    CAS  Google Scholar 

  10. Abu-Mulaweh HI (2003) A review of research on laminar mixed convection flow over backward- and forward-facing steps. Int J Thermal Sci 42:897–909

    Article  Google Scholar 

  11. Iwai H, Nakabe K, Suzuki K (2000) Flow and heat transfer characteristics of backward-facing step laminar flow in a rectangular duct. Int J Heat Mass Transfer 43:457–471

    Article  Google Scholar 

  12. Iwai H, Nakabe K, Suzuki K, Matsubara K (2000) The effects of duct inclination angle on laminar mixed convection flows over a backward-facing steps. Int J Heat Mass Transfer 43:473–485

    Article  Google Scholar 

  13. Armaly BF, Li A, Nie JH (2003) Measurements in three-dimensional laminar separated flow. Int J Heat Mass Transfer 46:3573–3582

    Article  Google Scholar 

  14. Tsui YY, Shu SJ (1998) Effects of buoyancy and orientation on the flow in a duct precede with a double step expansion. Int J Heat Mass Transfer 41(17):2687–2695

    Google Scholar 

  15. Yan WM (1995) Transport phenomena of developing laminar mixed convection heat and mass transfer in inclined rectangular ducts. Int J Heat Mass Transfer 38(15):2905–2914

    Article  Google Scholar 

  16. Gebhart B, Pera L (1971) The nature of vertical natural convection flows resulting from the combined buoyancy effects of thermal and mass diffusion. Int J Heat Mass Transfer 14:2025–2050

    Article  CAS  Google Scholar 

  17. Nelson AJ, Wood BD (1989) Combined heat and mass transfer natural convection between vertical parallel plates. Int J Heat Mass Transfer 32(9):1779–1787

    Article  CAS  Google Scholar 

  18. Baliga AR, Pham TT (1983) Solution of some two-dimensional incompressible fluid flow and heat transfer problems, using a control volume finite-element method. Numer Heat Transfer 6:263–282

    Google Scholar 

  19. Baliga AR, Patankar SV (1980) A new finite-element formulation for convection-diffusion problems. Numer Heat Transfer 3:393–409

    Google Scholar 

  20. Prakash B (1986) An improved control volume finite element method for heat and mass transfer, and for fluid flow using equal order velocity pressure interpolation. Numer Heat Transfer 9:253–276

    Google Scholar 

  21. Omri A, Nasrallah SB (1999) Control volume finite element numerical simulation of mixed convection in an air-cooled cavity. Numer Heat Transfer 36:615–637

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut Supérieur des Etudes Technologiques de Sousse, Sousse, Tunisia

    S. El Alimi

  2. Faculté des Sciences de Monastir, Tunisia

    J. Orfi

  3. Ecole Nationale d’Ingénieurs de Monastir, Tunisia

    S. Ben Nasrallah

Authors
  1. S. El Alimi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Orfi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Ben Nasrallah
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. El Alimi.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Alimi, S.E., Orfi, J. & Nasrallah, S.B. Buoyancy effects on mixed convection heat and mass transfer in a duct with sudden expansions. Heat Mass Transfer 41, 559–567 (2005). https://doi.org/10.1007/s00231-004-0566-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-004-0566-9

Keywords

Search

Navigation