Soret effect and slow mass diffusion as a catalyst for overstability in Marangoni-Bénard flows

Abstract.

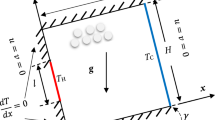
We study the onset of time dependent Marangoni-Bénard convection in binary mixtures subject to Soret effect by numerical computation of linear instability thresholds in infinite fluid layers and two-dimensional boxes. The calculations are done for positive Marangoni numbers (Ma > 0) and negative Marangoni Soret parameters S_M = –(D_Sγ_c)/(Dγ_T) where D_S and D are the Soret and mass diffusion coefficients, respectively, and γ_T, γ_c are the first derivatives of the surface tension with respect to temperature and concentration. Our purpose is to understand why for particular choices of Prandtl and Schmidt numbers, the increase of the stabilizing solutal contribution leads to a decrease of the critical temperature difference, a phenomenon already reported by Chen & Chen [5] and Skarda et al. [12] For various choices of Prandtl and Schmidt numbers we analyze the evolution of the critical Marangoni number Ma_c, critical wavenumber k_c and angular frequency ω_c with S_M and compute the corresponding eigenvectors. We next propose a physical mechanism which explains how the stabilizing solutal contribution acts as a catalyst for overstability. Finally, we extend our results to two dimensional boxes of small aspect ratio.

Appendix A

In the following, and for simplicity we drop the star from the notation and denote with the subscripts r and i the real and imaginary parts of the unknown functions respectively. Replacing the expansion of the variables into the linearized equations and identifying the real and imaginary parts of the resulting set of equations, we get the following ordinary differential equations:

$$ \eqalign{u^{\prime\prime}_r - k^2 u_r + kp_i = - \omega u_i, \cr u^{\prime\prime}_i - k^2 u_i - kp_r = \omega u_r, \cr w^{\prime\prime}_r - k^2 w_r - p^\prime_r = - \omega w_i , \cr w^{\prime\prime}_i - k^2 w_i - p^\prime_i = \omega w_r,} $$

$$\eqalign{- ku_i + w^\prime_r = 0, \cr ku_r + w^\prime_i = 0,} $$

$$\eqalign{ - Ma\,w_r + Pr^{-1} (T^{\prime \prime}_r - k^2 T_r) = - \omega T_i, \cr - Ma\,w_i + Pr^{-1} (T^{\prime \prime}_i - k^2 T_i) = \omega T_r,} $$

$$\eqalign{ - Ma\,w_r + Sc^{-1} (c^{\prime \prime}_r - T^{\prime \prime}_r - k^2 (c_r - T_r)) = -\omega c_i, \cr -Ma\,w_i + Sc^{-1} (c^{\prime \prime}_i - T^{\prime \prime}_i - k^2 (c_i - T_i)) = \omega c_r,} $$

along with the boundary conditions:

$$ u^{\prime}_r (1) + Pr^{-1} k(T_i (1) + S_M c_i (1)) = u^{\prime}_i (1) - Pr^{-1} k(T_r (1) + S_M c_r (1)) = u_r (0) = u_i (0) = 0, $$

$$ w_r (1) = w_i (1) = w_r (0) = w_i (0) = 0, $$

$$ \eqalign{p^{\prime}_r (1) + k^2 w_r (1) - w^{\prime\prime}_r (1) = p^{\prime}_i (1) + k^2 w_i (1) - w^{\prime\prime}_i (1) = p^{\prime}_r (0) + k^2 w_r (0) - w^{\prime\prime}_r (0) \cr = p^{\prime}_i (0) + k^2 w_i (0) - w^{\prime\prime}_i (0) = 0,} $$

$$ T_r (0) = T_i (0) = T^{\prime}_r (1) = T^{\prime}_i (1) = 0, $$

$$ T^{\prime}_r (0) - c^{\prime}_r (0) = T^{\prime}_i (0) - c^{\prime}_i (0) = T^{\prime}_r (1) - c^{\prime}_r (1) = T^{\prime}_i (1) - c^{\prime}_i (1) = 0. $$