Skip to main content
SpringerLink
Log in

A Skolem–Mahler–Lech theorem in positive characteristic and finite automata

  • Published:
Inventiones mathematicae Aims and scope

Abstract

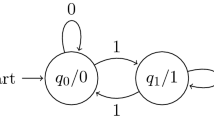
Lech proved in 1953 that the set of zeroes of a linear recurrence sequence in a field of characteristic 0 is the union of a finite set and finitely many infinite arithmetic progressions. This result is known as the Skolem–Mahler–Lech theorem. Lech gave a counterexample to a similar statement in positive characteristic. We will present some more pathological examples. We will state and prove a correct analog of the Skolem–Mahler–Lech theorem in positive characteristic. The zeroes of a recurrence sequence in positive characteristic can be described using finite automata.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramovich, D., Voloch, J.F.: Toward a proof of the Mordell–Lang conjecture in characteristic p. Int. Math. Res. Notices 5, 103–115 (1992)

    Article  MathSciNet  Google Scholar 

  2. Bell, J.: A generalized Skolem–Mahler–Lech theorem for affine varieties. math.NT/0501309 (preprint)

  3. Bézivin, J.-P.: Suites récurrentes linéaires en caractéristique non nulle. Bull. Soc. Math. France 115, 227–239 (1987)

    MATH  MathSciNet  Google Scholar 

  4. Eisenbud, D.: Commutative Algebra – with a View toward Algebraic Geometry. Springer, New York (1994)

    Google Scholar 

  5. Evertse, J.-H., Schlickewei, H.P.: The absolute subspace theorem and linear equations. In: Number Theory in Progress, vol. 1, pp. 121–142. de Gruyter, Berlin (1999)

  6. Evertse, J.-H., Schlickewei, H.P.: A quantitative version of the absolute subspace Theorem. J. Reine Angew. Math. 548, 21–127 (2002)

    MATH  MathSciNet  Google Scholar 

  7. Evertse, J.-H., Schlickewei, H.P., Schmidt, W.: Linear equations in variables which lie in a multiplicative group. Ann. Math. 155, 807–836 (2002)

    MATH  MathSciNet  Google Scholar 

  8. Furstenberg, H.: Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ (1981)

    MATH  Google Scholar 

  9. Everest, G., van der Poorten, A., Shparlinski, I., Ward, T.: Recurrence Sequences, Mathematical Surveys and Monographs, vol. 104. Am. Math. Soc., Providence, RI (2003)

    MATH  Google Scholar 

  10. Ghioca, D.: The isotrivial case in the Mordell–Lang Theorem. Preprint, to appear in Trans. Am. Math. Soc.

  11. Hrsushovski, E.: The Mordell–Lang conjecture for function fields. J. Am. Math. Soc 9(3), 667–690 (1996)

    Article  Google Scholar 

  12. Kitchens, B., Schmidt, K.: Mixing sets and relative entropies for higher-dimensional Markov shifts. Ergodic Theory Dyn. Syst. 13(4), 705–735 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  13. Lang, S.: Algebra. Graduate Texts in Mathematics, vol. 211, revised 3rd ed. Springer, New York (2002)

    MATH  Google Scholar 

  14. Lech, C.: A note on recurring series. Ark. Mat. 2, 417–421 (1953)

    MATH  MathSciNet  Google Scholar 

  15. Lewis, H., Papadimitriou, C.: Elements of the Theory of Computation. Prentice-Hall (1981)

  16. Mahler, K.: Eine arithmetische Eigenschaft der Taylor Koeffizienten rationaler Funktionen. Proc. Akad. Wet. Amsterdam 38, 51–60 (1935)

    Google Scholar 

  17. Mahler, K.: On the Taylor coefficients of rational functions. Proc. Cambridge Philos. Soc. 52, 39–48 (1956), Addendum: 53, 544 (1957)

  18. Masser, D.: Two letters to D. Behrend. September 12 and 19, 1985

  19. Masser, D.: Mixing and linear equations over groups in positive characteristic. Israel J. Math. 142, 189–204 (2004)

    MATH  MathSciNet  Google Scholar 

  20. Moosa, R., Scanlon, T.: F-structures and integral points on semi-abelian varieties over finite fields. Am. J. Math. 126, 473–522 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  21. Moosa, R., Scanlon, T.: The Modell–Lang conjecture in positive characteristic revisited. In: Model, Theory and Applications. Quad. Mat., vol. 11, pp. 273–296. Aracne, Rome (2002)

  22. van der Poorten, A.: Additive relations in number fields. Séminaire de théorie des nombres de Paris 1982–1983. Progress in Mathematics, pp. 259–266. Birkhäuser, Boston, MA (1984)

  23. Schlickewei, H.P., Schmidt, W.: The number of solutions of polynomial-exponential equations. Compos. Math. 120(2), 193–225 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  24. Schmidt, K.: Dynamical systems of Algebraic Origin. Prog. Math., vol. 128. Birkhäuser, Basel (1995)

    MATH  Google Scholar 

  25. Schmidt, W.: Heights of points on subvarieties of \(\mathbb{G}_{\textit{m}}^{\textit{n}}\). In: Number Theory (Paris, 1993–1994). London Math. Soc. Lecture Note Ser., vol. 235, pp. 157–187. Cambridge Univ. Press, Cambridge (1996)

  26. Schmidt, W.: The zero multiplicity of linear recurrence sequences. Acta Math. 182, 243–282 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  27. Schmidt, W.: Zeros of linear recurrence sequences. Publ. Math. 56, 609–630 (2000)

    MATH  Google Scholar 

  28. Skolem, T.: Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen. In: Comptes rendus du congrés des mathèmaticiens scandinaves, Stockholm, 1934, pp. 163–188. (1935)

  29. Stepanov, S., Shparlinski, I.: On the construction of a primitive normal basis of a finite field (Russian), Mat. Sb. 180(8), 1067–1972, 1151 (1989). Translation in Math. USSR-Sb. 67(2), 527–533 (1990)

  30. Stepanov, S., Shparlinski, I.: On the construction of primitive elements and primitive normal bases in a finite field. In: Computational Number Theory (Debrecen, 1989), pp. 1–14. de Gruyter, Berlin (1991)

  31. Szemerédi, E.: On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27, 199–245 (1975)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Michigan, Ann Arbor, USA

    Harm Derksen

Authors
  1. Harm Derksen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Harm Derksen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Derksen, H. A Skolem–Mahler–Lech theorem in positive characteristic and finite automata. Invent. math. 168, 175–224 (2007). https://doi.org/10.1007/s00222-006-0031-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-006-0031-0

Keywords

Search

Navigation