Introduction

For exact numerosity judgment, two enumeration processes have been identified: a fast and highly accurate process labeled ‘subitizing’ for enumeration of small numbers of items (<4) and a slower and more error-prone process referred to as ‘counting’ for larger numbers of items (Kaufman et al. 1949). This distinction between judgment of small and large numbers has not only been shown to exist in vision (Atkinson et al. 1976; Mandler and Shebo 1982; Trick and Pylyshyn 1993; Trick 2008), but also in audition (Ten Hoopen and Vos 1979) and more recently in touch (Riggs et al. 2006; Plaisier et al. 2009). The finding that subitizing occurs in touch is particularly interesting because it has been shown that parieto-frontal brain circuits dedicated to number processing partially overlap with those dedicated to hand and finger movements (Pinel et al. 2004; Piazza et al. 2002). The existence of interactions between visually perceived numbers and hand motor actions in terms of corticospinal excitability of the hand muscles and grip opening/closing has been shown in behavioral studies (Andres et al. 2004, 2007; Moretto and Di Pellegrino 2008). For mediating these interactions, it has been proposed that there is an analogue representation of magnitude in the parietal cortex (Walsh 2003). The existence of these interactions shows that visually perceived numbers can evoke action. What about numbers perceived through action? The question arises whether there are not only interactions between perceived numbers and action, but whether numbers perceived through active touch are processed in a similar way as visually perceived numbers. If so, this is an indication that magnitude representation in the parietal cortex is modality-independent. Although subitizing occurs in several modalities, it is not yet clear what kind of a process it actually is and how it is dissociated from counting. One thing that is clear from visual studies is that when observers are shown a field of dots, they do not simply add all the dots one by one to arrive at the total. Rather, they seem to enumerate small groups of dots and sum the groups to arrive at the total (Van Oeffelen and Vos 1982, 1984). Consequently, enumeration of large fields of dots can be affected by the spatial arrangement of the dots.

In a previous study on haptic numerosity judgment, we have shown that subitizing occurred for up to three items when subjects were asked to enumerate a number of spheres grasped together in the hand (Plaisier et al. 2009). Now the question arises whether subitizing and counting are implemented in a similar way for visual and haptic perception of numbers. If this is the case, the group-and-add strategy observed in visual studies should also be possible in the haptic case. To answer this question, we presented subjects with varying numbers of spheres that were explored using active touch. In order to cluster sets of items together, we presented a set of spheres to each hand of the subjects. Either one set of spheres was presented to the left or right hand of the subjects (unimanual trials), or two sets were presented to each hand simultaneously (bimanual trials).

The results from the unimanual trials were used to model number processing in the bimanual case. We hypothesize three mutually exclusive outcomes. The first possibility is that subitizing is inhibited because information from both hands is combined in an inefficient way. The second possibility is that subitizing does occur, but subitizing or counting is used depending on the total number of spheres and not cluster size. Finally, there is the possibility that it depends on cluster size on which enumeration mechanism is used. If this third hypothesis is true, then this shows that configurational effects found in vision also occur in touch and that numbers can be processed through a combination of subitizing and counting. Such similarities between haptic and visual enumeration would be strong evidence for a modality-independent model of number processing and consequently that magnitude representation is modality-independent.

Method

Participants

Ten paid subjects participated in the experiment. All participants were right-handed according to Coren’s test (1993) and none of them had any known hand deficits. All subjects were naive as to the purpose of the experiment and signed a declaration of informed consent.

Set-up

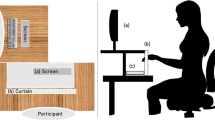
The items consisted of brass spheres (1.86 cm diameter, 29 g) suspended from flexible wires (Fig. 1a). These same spheres were used in our previous study into haptic numerosity judgment (Plaisier et al. 2009). A custom-built device was used to measure the response times. Time measurement was started automatically when a subject touched the stimuli and it was terminated through a vocal response. The response times were measured with an accuracy of 10 ms. For technical details about this device, see Plaisier et al. (2008).

Fig. 1
figure 1

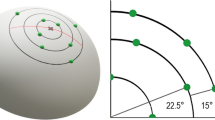
a Picture of a subject grasping upwards to start a bimanual trial. b All presented combinations of numerosities in the right and left hand are indicated with a plot mark. Combinations for which the numerosity in the left or right hand was zero were unimanual and marked with dots. The other symbols indicate the bimanual combinations. Here, subitizing up to three items is assumed. In that case, the triangles indicate that both clusters were in the subitizing range and crosses indicate that both clusters were in the counting range. Squares indicate that there was one cluster from the counting range and one from the subitizing range, where a black-filled square indicates that the smallest cluster had 1 item, a grey-filled square indicates this cluster had two items and a white-filled square indicates that the smallest cluster had three items. c Predicted response times for bimanual trials from three different models using the slopes and offset values from the unimanual trials. Regression parameters determined from the unimanual trials were entered into each of the models to arrive at predictions of the absolute response times. There were different combinations of clusters that summed up to the same total number of spheres. The predicted response times can therefore fall on top of each other. ‘No subitizing’ indicates the prediction of the response times if subitizing does not occur in bimanual number processing. ‘Total numerosity dependent’ shows the predicted response times in the case that subitizing can be used and the enumeration mechanism that is used depends only on the total number of spheres. ‘Cluster size dependent’ indicates the prediction of the response times in the case that subitizing can be used and the selected enumeration process depends on the cluster size in each hand. In this case, response times depend on the specific numerosity combination and therefore different plot symbols were used for different numerosity combinations. See text for further explanation of the models

Full size image

Experimental design

Subjects were blindfolded and wore earplugs to eliminate sound cues. They placed their left hand in a holder on the left side and the right hand in a holder on the right side. Sets of spheres could be suspended above these holders. The experimenter informed the subject before the trial started whether the spheres were on both sides and otherwise on which side the spheres were. If there was only one set of spheres, the subjects were instructed to grasp upwards with the corresponding hand and respond the correct number of spheres as fast as possible. When there were two sets of spheres, subjects were instructed to grasp upwards with both hands simultaneously and respond the total number of spheres (i.e. the sum of the spheres in the left and right hands). After each trial, subjects were told what the correct number of spheres was. There were no restrictions on exploratory strategy nor on hand movements, other than having to initially grasp all items simultaneously. After initially grasping all items it was allowed to release spheres from their hand during a trial, but subjects were instructed to only do this if they thought that this was the fastest strategy.

Subjects were presented with a total number of spheres ranging from 1 to 12. These numerosities were either presented to one hand (unimanual) or divided over both hands (bimanual). Each combination indicated in Fig. 1b was presented five times, except for those on the diagonal (e.g. 4 left and 4 right), which were presented 10 times. This means that when the trials are collapsed over both hands, each numerosity combination was presented 10 times. Note that these combinations allow comparison of enumeration of each total numerosity in the unimanual case to the bimanual case, except for when the total numerosity was one. Each subject performed a total of 330 trials (= 24 × 5 unimanual + 30 × 5 bimanual + 6 × 10 bimanual) divided over three blocks of trials of approximately 1 h. Trials were performed in pseudo-random order such that each numerosity was presented roughly the same number of times in each block. The blocks of trials were performed on different days or with a break of at least 2 h in between. To get comfortable with the task and procedure, subjects performed 20 practice trials before the first block of trials was started and practice trials were continued until 10 in a row had been answered correctly. It was never necessary to exceed 30 practice trials. During practice trials subjects were presented with a random selection of all possible combinations. This means that unimanual and bimanual trials were interleaved like in the main experiment. Error trials were repeated at the end of the block to ensure an equal number of correct trials for all numerosity combinations.

Analysis

Because subjects were instructed to minimize the number of errors, error rates should be generally low and the response times are used for further analysis. Only response times from correctly answered trials were included in the analysis. For the unimanual trials, we assume a bilinear function for the response times as a function of the number of spheres (Plaisier et al. 2009). The slope of the first linear part represents the subitizing slope and the slope of the second linear part represents the counting slope. This function is defined as:

$$ T_{\rm uni}(N) = (s_s N + c_1) H\left({\frac{c_2-c_1}{s_s - s_c}} - N\right)+(s_c N + c_2) H\left(N - {\frac{c_2-c_1}{s_s - s_c}}\right). $$
(1)

Here N is the presented number of spheres, H(N) is the Heaviside step function, s s and s c are the subitizing and counting slopes, respectively, and c 1 and c 2 represent constant offsets. Note that through this analysis, the location of the transition point follows from the intersection of the two linear parts and is given by:

$$ N_{t} = \left({\frac{c_2-c_1}{s_s - s_c}} \right). $$
(2)

Regression of this function allowed the slopes to be determined without making assumptions about the transition point which is determined by the fitting parameters from the linear parts. The slope values from the unimanual trials were used to model the bimanual response times.

Bimanual models

For the bimanual trials, three hypotheses were discussed in the Introduction. The case in which subitizing does not occur and counting is used over the whole numerosity range is represented by the ‘No subitizing’ model (Fig. 1c, top graph). The response time as a function of the number of spheres in the left hand (n 1) and the right hand (n 2) is given by:

$$ T_{\rm bi}(n_{1}, n_{2}) = c_{1} + s_{c} (n_{1}+n_{2}) $$
(3)

The second possibility is that subitizing can be used and the enumeration process depends on the total numerosity only (Fig. 1c, middle graph). This means that if the total numerosity is in the subitizing range the total is subitized, while if the total is in the counting range it is counted regardless of the sizes of the clusters in the two hands. This ‘Total numerosity dependent’ model is expressed in terms of the response time function for the unimanual case as:

$$ T_{\rm bi}(n_{1}, n_{2}) = T_{\rm uni}(n_{1}+n_{2}) $$
(4)

The last hypothesis is that subjects use either subitizing or counting depending on the cluster size. Both clusters are summed to arrive at the number of spheres. The expected response times from this ‘Cluster size dependent’ model are shown in the bottom graph of Fig. 1c and are given by:

$$ T_{\rm bi}(n_{1}, n_{2}) = T_{\rm uni}(n_{1}) + T_{\rm uni}(n_{2}) - c_{1} $$
(5)

The time that is needed to sum the two clusters to arrive at the total is neglected. The constant offset c 1 is subtracted once, because otherwise it would be included twice in the response time.

Results

Overall

A 2 × 12 (condition × total numerosity) repeated measures ANOVA on the response times from the unimanual and bimanual trials collapsed over both hands showed main effects for condition [F(1, 9) = 122, p < 0.0001, η 2 p = 0.93] as well as numerosity [F(1.6, 14.8) = 447, p < 0.0001, η 2 p = 0.98, Greenhouse-Geisser corrected values] and an interaction effect [F(2.0, 18.4) = 18.4, p < 0.0001, η 2 p = 0.78, Greenhouse-Geisser corrected values]. Error rates were well below chance for all numerosities (<11% unimanual and <7% bimanual) and no errors were made for up to three items (Fig. 2a). A paired samples t test on the error rates averaged over all total numerosities for the unimanual and bimanual trials showed that error rates were significantly lower in the bimanual condition (t(9) = 2.4, p = 0.04).

Fig. 2
figure 2

a Error rates averaged over subjects as a function of the total number of spheres in the unimanual (light grey bars) and bimanual trials (dark grey bars). b Response times averaged over subjects as a function of the number of spheres. The spheres were all presented to either the left or the right hand. The error bars indicate the SD of the single subject means. The solid line represents weighted regression of the bilinear function to the response times. The resulting slope values are indicated in the figure. c Response times averaged over subjects for the bimanual trials as a function of the total presented numerosity. Plot symbols correspond to those in Fig. 1. d Response times averaged over subjects as a function of the presented numerosity combination (black dots). The error bars indicate the SD of the distribution of the single subject means. The light gray dots indicate the predicted response times from the ‘Cluster size dependent’ model

Full size image

Unimanual trials

To test whether there was an advantage for the left or right hand for subitizing or counting, the average response times for the subitizing and counting range were calculated for the left and right hand separately for each subject. A repeated measures ANOVA with hand and numerosity as factors was performed on these values. As expected, there was a main effect of numerosity (F(1.6, 14) = 266, p < 0.0005, η 2 p = 0.98, Greenhouse-Geisser corrected values). There was no effect of hand (F(1, 9) = 0.03, p = 0.86, η 2 p = 0.004), nor was there an interaction between hand and numerosity (F(3.0, 27.3) = 1.8, p = 0.17, η 2 p = 0.17, Greenhouse-Geisser corrected values). To determine the subitizing and counting slopes, the data from the two hands were collapsed and averaged over subjects (Fig. 2b). The bilinear function (Eq. 1) was fitted to the averaged response times weighted according to the inverse squared standard deviations (R 2 = 0.90). The transition point was found to be at 3.3 ± 0.2 items, which is in between 3 and 4 items as expected. The resulting subitizing and counting slope values were 0.20 ± 0.03 s/item and 1.2 ± 0.2 s/item, respectively. The uncertainties reported here indicate the SE of the fitting parameters and result directly from the fitting procedure. The slope values found here are comparable to the subitizing and counting slopes of 0.16 s/item and 0.84 s/items found in our previous study on haptic numerosity judgment (Plaisier et al. 2009). There was a small negative correlation between trial number and response times normalized for the different numerosities (r = −0.1, p < 0.001). Response times were on average 9% faster in the last trial than in the first trial. This indicates a small learning effect that is probably due to subjects gaining experience in handling the objects.

Bimanual trials

The response times averaged over subjects as a function of the total number of spheres is shown in Fig. 2c. In this case, several combinations were possible to arrive at the same total number of spheres. Response times from combinations with the numerosities in the left and right hand reversed (e.g. 3–1 and 1–3) were collapsed. Comparison of the pattern in the response times to those predicted by the models in Fig. 2 suggests that the ‘Cluster size dependent’ model performs best. R 2 values were calculated to compare performance of the three models. Note that there were no free parameters in the models and therefore R 2 values can be negative and even smaller than −1. Negative values indicate that the data is better described by the mean than by the model. The largest possible R 2 value is 1, which means that the data follows the model exactly. For the ‘No subitizing’ model, this yielded R 2 = −14, for the ‘Total numerosity dependent’ model this yielded R 2 = −0.55 and R 2 = 0.93 for the ‘Cluster size dependent’ model. This analysis clearly shows that indeed the ‘Cluster size dependent’ model performs best. The response times as a function of the numerosity combinations and the model predictions are shown in Fig. 2d. Considering the fact that there were no free parameters, the R 2 value is remarkably high, which indicates that this model predicts the absolute response times very accurately. Also, the good performance of the model at describing the absolute response times shows that the time needed to sum the numerosities from both hands is indeed negligible. In fact, it can be seen in Fig. 2d that when there were clusters from the counting range, the predicted response times were somewhat larger than the measured response times indicating that bimanual number processing occurs partially in parallel. As there was in the unimanual case, there was also a small negative correlation between trial number and the normalized response times (r = −0.2, p < 0.001) in the bimanual case. Response times were on average 17% faster in the last trial than in the first trial. This indicates that there was a stronger learning effect than in the unimanual trials. Besides gaining experience in object handling, in the bimanual case also addition times of the numerosities from both hands probably decreased.

Discussion

From the bimanual trials, it was concluded that the ‘Cluster size dependent’ model performs best. This not only shows that subitizing occurs for bimanual processing of numbers but also that each cluster is either subitized or counted depending on the cluster size. Both clusters are summed to arrive at the total. Consequently, clustering the items enables subitizing for up to six items and reduces response times for larger numerosities considerably compared to the unimanual case. Note that clustering the items also reduced response times for trials in which both cluster sizes were in the counting range, compared to the unimanual trials. An explanation for this is that the response times in the counting range for the unimanual case are a combination of subitizing three items and counting and adding the remaining items. In the bimanual case, three items are subitized and the remaining items are counted for both hands. This way a total of six items were processed through subitizing and fewer items remained to be counted than in the unimanual case. This clearly demonstrates that enumeration of numerosities from the counting range is performed through a combination of subitizing and counting also when all items are in one hand.

The fact that subitizing is used in combination with counting has also been suggested in vision where a group-and-add procedure is found to be used (Van Oeffelen and Vos 1982, 1984). This fact complicates dissociation between the activated brain areas for both processes. In a brain imaging study by Piazza et al. (2002), no evidence was found for the existence of a neural network dedicated specifically to subitizing and that was not activated during counting. This is in agreement with the idea that subitizing is actually a sub-process of counting. Our results show that this is also the case in haptic numerosity judgment.

In conclusion, we have shown that response times are reduced considerably in bimanual number processing and that the subitizing range can be extended up to six items. Furthermore, we have shown that subitizing is involved in the processing of numerosities from the counting range. This shows that the group-and-add strategy found in vision is also used in touch. This provides strong evidence that numerosity is processed in a highly similar way for vision and active touch. Consequently, there is not only an influence of perception of numbers on hand motor action, but rather, numbers perceived through hand motor action are processed in the same way as visually perceived numbers. This suggests that magnitude representation is modality-independent.