Skip to main content
SpringerLink
Log in

Formal Expansions in Stochastic Model for Wave Turbulence 1: Kinetic Limit

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

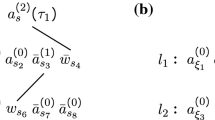
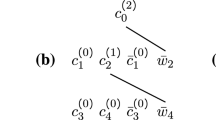
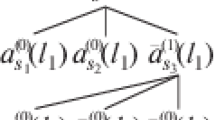Abstract

We consider the damped/driven (modified) cubic NLS equation on a large torus with a properly scaled forcing and dissipation, and decompose its solutions to formal series in the amplitude. We study the second order truncation of this series and prove that when the amplitude goes to zero and the torus’ size goes to infinity the energy spectrum of the truncated solutions becomes close to a solution of the damped/driven wave kinetic equation. Next we discuss higher order truncations of the series.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Note in addition that if u(t, x) satisfies eq. (1.2), then \(u'= e^{ 2it\lambda \Vert u \Vert ^2}u\) is a solution of (1.1).

  2. The symmetric form of the Fourier transform which we use—with the same scaling factor \( L^{-d/2}\) for the direct and the inverse transformations—is convenient for the heavy calculation below in the paper.

  3. i.e. \(\beta _s = \beta _s^1 + i\beta _s^2\), where \(\{\beta _s^j, s\in {\mathbb {Z}}^d_L, j=1,2 \}\) are standard independent real Wiener processes.

  4. For example, if \(\gamma _s = (1+ |s|^2)^{r_*}\), then \(\mathfrak {A}= (1-\Delta )^{r_*}\).

  5. Indeed, denoting \(\xi =(x,\bar{\eta })\) we see that the first fundamental form \(I^\xi \) of \(\Sigma ^x\) is given by \(I^\xi _{ij} =(\delta _{i,j} +\theta _i\theta _j)\), where \(\theta = \partial _\xi \varphi \in \mathbb {R} ^{2d-1}\). So for \(X\in \mathbb {R} ^{2d-1}\),

    $$\begin{aligned} I^\xi (X,X) = \sum X_j^2 + \sum _{i,j} X_i\theta _i X_j\theta _j = \sum X_j^2 +(X\cdot \theta )^2. \end{aligned}$$

    Choosing in \( \mathbb {R} ^{2d-1} \) a coordinate system with the first basis vector \(\theta /|\theta |\) we find that \( I^\xi (X,X) = X_1^2(1+|\theta |^2) + \sum _{j\ge 2} X_j^2\). So det\(I^\xi = 1+| \partial _\xi \varphi |^2\), which implies the formula for the density \(\bar{p}\).

  6. This is true for the most of Wick-pairings, while for some of them the affine space of variables may become empty because of the restrictions of the type \(\{s_1,s_2\}\ne \{s_3,s\}\) imposed by \(\delta '^{12}_{3s}\).

References

  1. Arnold, V.I., Kozlov, V.V., Neistadt, A.I.: Mathematical Aspects of Classical and Celestial Mechanics, 3d edn. Springer, Berlin (2006)

    Book  Google Scholar 

  2. Bourgain, J.: Global Solutions of Nonlinear Schrödinger Equations. AMS, Providence (1999)

    Book  Google Scholar 

  3. Falkovich, G.: Introduction to Turbulence Theory, pp. 1–43 of the Book Cardy, J., Falkovich, G., Gawedzki, K. Non-equilibrium Statistical Mechanics and Turbulence. Cambridge University Press, Cambridge (2008)

  4. Buckmaster, T., Germain, P., Hani, Z., Shatah, J.: Onset of the wave turbulence description of the longtime behaviour of the nonlinear Schrödinger equation (2019). arXiv:1907.03667

  5. Dimassi, M., Sjöstrand, J.: Spectral Asymptotic in the Semi-Classical Limit. CUP, Cambridge (1999)

    Book  Google Scholar 

  6. Dymov, A.: Nonequilibrium statistical mechanics of weakly stochastically perturbed system of oscillators. Ann. Henri Poincaré 17, 1825–1882 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  7. Dymov, A.V.: Asymptotic estimates for singular integrals of fractions whose denominators contain products of block quadratic forms. Proc. Steklov Inst. Math. 310, 148–162 (2020)

    Article  MathSciNet  Google Scholar 

  8. Dymov, A., Kuksin, S.: Formal expansions in stochastic model for wave turbulence 2: method of diagram decomposition (2019). arXiv:1907.02279

  9. Eckmann, J.-P., Pillet, C.-A., Rey-Bellet, L.: Non-equilibrium statistical mechanics of anharmonic chains coupled to two heat baths at different temperatures. Commun. Math. Phys. 201, 657–697 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  10. Faou, E.: Linearized wave turbulence convergence results for three-wave systems. Commun. Math. Phys. 378, 807–849 (2020)

    Article  MathSciNet  Google Scholar 

  11. Faou, E., Germain, P., Hani, Z.: The weakly nonlinear large-box limit of the 2D cubic nonlinear Schrödinger equation. J. Am. Math. Soc. 29, 915–982 (2016)

    Article  Google Scholar 

  12. Gelfand, I.M., Shilov, G.E.: Generalised Functions, volume 1: Properties and Operations. AMS Chelsea Punlishing, New York (1964)

    Google Scholar 

  13. Huang, G., Kuksin, S., Maiocchi, A.: Time-averaging for weakly nonlinear CGL equations with arbitrary potentials. Fields Inst. Commun. 75, 323–349 (2015)

    Article  MathSciNet  Google Scholar 

  14. Hörmander, L.: The Analysis of Linear Partial Differential Operators, vol. 1. Springer, Berlin (1983)

    MATH  Google Scholar 

  15. Janson, S.: Gaussian Hilbert Spaces. CUP, Cambridge (1997)

    Book  Google Scholar 

  16. Kartashova, E.: Discrete wave turbulence. Europhys. Lett. 87, 44001 (2009)

    Article  ADS  Google Scholar 

  17. Khinchin, A.I.: Mathematical Foundations of Statistical Mechanics. Dover, New York (1949)

    MATH  Google Scholar 

  18. Komorowski, T., Olla, S., Ryzhik, L.: Asymptotics of the solutions of the stochastic lattice wave equation. Arch. Ration. Mech Anal. 209, 455–494 (2013)

    Article  MathSciNet  Google Scholar 

  19. Kuksin, S.: Asymptotical expansions for some integrals of quotients with degenerated divisors. Russ. J. Math. Phys. 24, 497–507 (2017)

    Article  Google Scholar 

  20. Kuksin, S.: Asymptotic properties of integrals of quotients, when the numerator oscillates and denominator degenerate. J. Math. Phys. Anal. Geom. 14, 510–518 (2018)

    MathSciNet  MATH  Google Scholar 

  21. Kuksin, S., Maiocchi, A.: Derivation of a wave kinetic equation from the resonant-averaged stochastic NLS equation. Physica D 309, 65–70 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  22. Kuksin, S., Maiocchi, A.: Resonant averaging for small solutions of stochastic NLS equations. Proc. R. Soc. Edinb. 147A, 1–38 (2017)

    Google Scholar 

  23. Lukkarinen, J., Spohn, H.: Weakly nonlinear Schrödinger equation with random initial data. Invent. Math. 183, 79–188 (2015)

    Article  ADS  Google Scholar 

  24. Nazarenko, S.: Wave Turbulence. Springer, Berlin (2011)

    Book  Google Scholar 

  25. Newell, A.C., Rumpf, B.: Wave turbulence. Annu. Rev. Fluid Mech. 43, 59–78 (2011)

    Article  ADS  MathSciNet  Google Scholar 

  26. Zakharov, V., L’vov, V.: Statistical description of nonlinear wave fields. Radiophys. Quan. Electron. 18, 1084–1097 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  27. Zakharov, V., L’vov, V., Falkovich, G.: Kolmogorov Spectra of Turbulence. Springer, Berlin (1992)

    Book  Google Scholar 

Download references

Acknowledgements

AD was supported by the Grant of the President of the Russian Federation (Project MK-1999.2021.1.1) and by the Russian Foundation for Basic Research (Project 18-31-20031), and SK – by Agence Nationale de la Recherche through the grant 17-CE40-0006. We thank Johannes Sjöstrand for discussion and an anonymous referee for careful reading of the paper and pointing out some flaws.

Author information

Authors and Affiliations

  1. Steklov Mathematical Institute of RAS, Moscow, Russia, 119991

    Andrey Dymov

  2. National Research University Higher School of Economics, Moscow, Russia, 119048

    Andrey Dymov

  3. UFR de Mathématiques - Batiment Sophie Germain, Université Paris-Diderot (Paris 7), 5 rue Thomas Mann, 75205, Paris, France

    Sergei Kuksin

  4. School of Mathematics, Shandong University, Jinan, People’s Republic of China

    Sergei Kuksin

Authors
  1. Andrey Dymov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sergei Kuksin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergei Kuksin.

Additional information

Communicated by C. Liverani.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dymov, A., Kuksin, S. Formal Expansions in Stochastic Model for Wave Turbulence 1: Kinetic Limit. Commun. Math. Phys. 382, 951–1014 (2021). https://doi.org/10.1007/s00220-021-03955-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-021-03955-w

Search

Navigation