Abstract
We prove that the existence of a dispersionless Lax pair with spectral parameter for a nondegenerate hyperbolic second order partial differential equation (PDE) is equivalent to the canonical conformal structure defined by the symbol being Einstein–Weyl on any solution in 3D, and self-dual on any solution in 4D. The first main ingredient in the proof is a characteristic property for dispersionless Lax pairs. The second is the projective behaviour of the Lax pair with respect to the spectral parameter. Both are established for nondegenerate determined systems of PDEs of any order. Thus our main result applies more generally to any such PDE system whose characteristic variety is a quadric hypersurface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
The integrability of dispersionless partial differential equations is well known to admit a geometric interpretation. Twistor theory [26, 29] gives a framework to visualize this for several types of integrable systems, as demonstrated by many examples [2, 10, 11, 14, 19, 30, 37].
Recently, such a relation has been established for several classes of second order equations in 3D and one class in 4D [17]. Namely the following equivalences have been established:

Hydrodynamic integrability in 2D (also written “\(1+1\) dimension”) was introduced in [9] and elaborated in [35]. Integrability via hydrodynamic reductions in \(d\geqslant 3\) dimensions was developed in [16]. This method, although constructive, is not universal, as it applies only to translation invariant equations (invariantly, this requires the existence of a d-dimensional abelian contact symmetry group). Thus the upper part of the above diagram, at least at present, does not extend to the general class of second order PDEs.
On the other hand, the two other ingredients of the diagram are universal. The main aim of this paper is to prove the bottom equivalence for large class of PDE systems, including general second order PDEs, in 3D and 4D, where “integrable background geometry” means that a canonical conformal structure on solutions of the equation is Einstein–Weyl in 3D and self-dual in 4D (these geometries are “backgrounds” for integrable gauge theories [2]).
Consider a second order PDE
for a scalar function u of an independent variable \({{\varvec{x}}}\) on a connected manifold M with \(\dim M=d\), where \(\partial u=(u_i)\) and \(\partial ^2u=(u_{ij})\) denote partial derivatives of u in local coordinates \({{\varvec{x}}}=(x^i)\). Let \(M_u\) denote the manifold M equipped with a given scalar function u; concretely, we may view \(M_u\) as the graph of u in \(M\times {{\mathbb {R}}}\). A tensor on \(M_u\) is, by definition, a tensor on M, which may also depend, at each \({{\varvec{x}}}\in M\), on finitely many derivatives of u at \({{\varvec{x}}}\).
Let \(\sigma _F\) be the linearization of F in second derivatives, i.e.,
Invariantly, \(\sigma _F\) defines a section of \(S^2T M_u\), hence a quadratic form on \(T^*_{{\varvec{x}}}M_u\) for each \({{\varvec{x}}}\in M_u\), called the symbol of F. If we change the defining function F of \({{\mathcal {E}}}\), \(\sigma _F\) changes by a conformal rescaling on \({{\mathcal {E}}}\). Hence the conformal class of \(\sigma _F\) along \(F=0\) is an invariant of \({{\mathcal {E}}}\), as is the characteristic variety \(\chi ^{{\mathcal {E}}}\rightarrow M_u\), the bundle whose fibre at \({{\varvec{x}}}\in M_u\) is the projective variety \(\chi ^{{\mathcal {E}}}_{{\varvec{x}}}:=\mathop {\mathrm {Char}}\nolimits ({{\mathcal {E}}},u)_{{{\varvec{x}}}}=\{[\theta ]\in {{\mathbb {P}}}(T^*_{{\varvec{x}}}M_u)\,|\, \sigma _F(\theta )=0\}\).
We assume henceforth that (1) is:
-
nondegenerate, i.e., \(\sigma _F\) is nondegenerate at generic points of the zero-set \({{\mathcal {E}}}\) of F. This is equivalent to \(\det (\sigma _{ij}(u))\ne 0\) for a generic solution u.
-
hyperbolic, i.e., M is complex and F is holomorphic, or M is real, F is smooth and the variety \(\{[\theta ]\in {{\mathbb {P}}}(T^*M_u\otimes {{\mathbb {C}}})\,|\, \sigma _F(\theta )=0\}\) of complex characteristics is a complexification of \(\chi ^{{\mathcal {E}}}\) for a generic (real) solution u.
The nondegeneracy of \(\sigma _F\) implies that its inverse

defines a nondegenerate symmetric bilinear form on \(T_{{\varvec{x}}}M_u\) for any \(({{\varvec{x}}},u)\) sufficiently close to a generic point of \(F=0\). As in [17], the corresponding conformal structure \(c_F\) plays a central role in this paper. Hyperbolicity implies that along \(F=0\), \(c_F\) is uniquely determined by the bundle \(\chi ^{{\mathcal {E}}}\) of nonsingular quadric hypersurfaces because the latter is dual to the projectivized null cone of \(c_F\).
A dispersionless Lax pair [38] or dLp for (1) can be described as rank one covering system [36] of \({{\mathcal {E}}}\). Roughly speaking, this means that there is a fibre bundle \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) with connected rank one fibres, and a PDE system on \({\hat{M}}_u\) with \({{\mathcal {E}}}\) as a differential corollary. There are various ways to formulate this precisely; in this paper we adopt as a definition that there are linearly independent vector fields \({\hat{X}}\) and \({\hat{Y}}\) on \({\hat{M}}_u\), whose coefficients depend on finitely many derivatives of u, such that \({{\mathcal {E}}}\) is the Frobenius integrability condition for their span \({\hat{\Pi }}\subseteq T{\hat{M}}_u\)—this is the condition that \([\hat{X},{\hat{Y}}]\) is a section of \({\hat{\Pi }}\), so that \({\hat{\Pi }}\) is tangent to a foliation of \({\hat{M}}_u\) by surfaces.
The leaf space of this foliation (for a solution u of \({{\mathcal {E}}}\)) is sometimes called the twistor space \({{\mathcal {T}}\!w}\) of the dLp in 4D (or minitwistor space in 3D). However, a well-behaved twistor space may only exist over suitable open subsets of \(M_u\), so its geometry is more conveniently described on the correspondence space \({\hat{M}}_u\). For instance, functions on \({{\mathcal {T}}\!w}\) correspond to solutions of a linear PDE system for functions on \({\hat{M}}_u\) that are constant on the leaves of the foliation, while hypersurfaces in \({{\mathcal {T}}\!w}\) may be described as solutions of a quasilinear PDE system for sections of \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) that are unions of such leaves. Either of these PDE systems can equivalently be called a dLp: \({{\mathcal {E}}}\) ensures their compatibility.
A fibre coordinate \(\lambda :{\hat{M}}_u\rightarrow {{\mathbb {R}}}\) is called a spectral parameter and it locally identifies \({\hat{M}}_u\) with \(M_u\times {{\mathbb {R}}}\). We may then write \({\hat{X}}=X+m\,\partial _\lambda \), \({\hat{Y}}=Y+n\,\partial _\lambda \) where X, Y are \(\lambda \)-parametric vector fields on \(M_u\), and a section of \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) may be written \(\lambda =q({{\varvec{x}}})\) for a function \(q:M_u\rightarrow {{\mathbb {R}}}\). The dLp \({\hat{\Pi }}\) then has the geometric interpretation that \({{\mathcal {E}}}\) is the integrability condition for the existence of many foliations of \(M_u\) by surfaces which are tangent at any \({{\varvec{x}}}\in M_u\) to the span \(\Pi ={\hat{\pi }}_*({\hat{\Pi }})\) of X and Y at \({{\varvec{x}}}\), with \(\lambda =q({{\varvec{x}}})\).
A fundamental motivation for this paper is that in all known examples of such dLps, it has been observed (see e.g. [17]) that \(\Pi \) is characteristic for \({{\mathcal {E}}}\) in the sense that for any solution u, and any 1-form \(\theta \) on \(M_u\) with \(\Pi \subseteq \ker \theta \), we have \([\theta ]\in \chi ^{{\mathcal {E}}}\). Thus for any solution u of \({{\mathcal {E}}}\), \(M_u\) admits many foliations by characteristic surfaces, and indeed \({{\mathcal {E}}}\) is the integrability condition for their existence. Our first result establishes this characteristic property in considerable generality.
Theorem 1
Let \(\hat{\Pi }\) be a dLp on \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) for a determined PDE system \({{\mathcal {E}}}\) of order \(\ell \) on \(M_u\). Then \(\Pi ={\hat{\pi }}_*({\hat{\Pi }})\) is characteristic for \({{\mathcal {E}}}\).
We refer to Sects. 2 and 3, or [21, 22, 36], for discussion of more general PDE systems and their characteristic varieties: in this introduction, we focus on second order scalar PDEs. For such PDEs, the characteristic condition means that for each solution u and each \({\hat{{{\varvec{x}}}}}\in {\hat{M}}_u\), \(\Pi _{{\hat{{{\varvec{x}}}}}}\) is a coisotropic 2-plane for the conformal structure \(c_F\). By nondegeneracy of \(c_F\), such 2-planes can only exist for \(2\leqslant d\leqslant 4\): for \(d=2\), the condition is vacuous; for \(d=3\), \(\Pi _{{\hat{{{\varvec{x}}}}}}\) is then tangent to the null cone of \(c_F\) (i.e., degenerate); for \(d=4\), \(\Pi _{{\hat{{{\varvec{x}}}}}}\) is then contained in the null cone (i.e., totally isotropic). In the real case, the characteristic condition further implies that \(c_F\) has (up to sign) signature (2, 1) for \(d=3\) or (2, 2) for \(d=4\). We assume this henceforth.
For both \(d=3\) and \(d=4\), the coisotropic 2-planes at each point \({{\varvec{x}}}\in M\) form a 1-dimensional submanifold of the grassmannian \(\mathop {\mathrm {Gr}}\nolimits _2(T_{{{\varvec{x}}}}M)\). For \(d=3\) this submanifold is a rational curve (\(\cong {{\mathbb {P}}}^1\), the projective line) canonically isomorphic to the conic \(\chi ^{{\mathcal {E}}}\subseteq {{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M)\). For \(d=4\), it is a disjoint union of two rational curves, corresponding to the two rulings of the quadric surface \(\chi ^{{\mathcal {E}}}\); the points of the two components are called \(\alpha \)-planes and \(\beta \)-planes depending on whether the 2-planes are self-dual or anti-self-dual.
If \(\Pi \) is coisotropic and is also an immersion, we may thus identify \({\hat{M}}_u\) locally with the \({{\mathbb {P}}}^1\)-bundle whose fibre over \({{\varvec{x}}}\in M_u\) consists of all coisotropic 2-planes for \(d=3\) or the \(\alpha \)-plane component for \(d=4\). Under this identification, \(\Pi \rightarrow {\hat{M}}_u\) becomes the tautological bundle of coisotropic 2-planes. Any Weyl connection \(\nabla \) on \(M_u\) (a torsion-free conformal connection on M depending on finitely many derivatives of u) induces a connection on \({\hat{M}}_u\rightarrow M_u\) and hence a horizontal lift of \(\Pi \) to distribution \({\hat{\Pi }}_\nabla \subseteq T{\hat{M}}_u\).
If \(d=4\), it is well-known [29] that \({\hat{\Pi }}_\nabla \) is independent of \(\nabla \) (i.e., conformally invariant), and is integrable if and only if \((M_u,c_F)\) is is self-dual (SD), i.e., the Weyl tensor \(W_{c_F}\) satisfies \(W_{c_F}=*W_{c_F}\). The integral surfaces of \({\hat{\Pi }}_\nabla \) then project to \(\alpha \)-surfaces for \(c_F\).
If \(d=3\), it is similarly well known [5, 19] that \({\hat{\Pi }}_\nabla \) is integrable if and only if \((M_u,c_F,\nabla )\) is Einstein–Weyl (EW), i.e., the symmetrized Ricci tensor of \(\nabla \) is proportional to any metric \(g_F\) in the conformal class: \(\mathop {\mathrm {Sym}}\nolimits (\mathop {\mathrm {Ric}}\nolimits ^\nabla )=\Lambda \, g_F\), \(\Lambda \in C^\infty (M_u)\). The integral surfaces of \({\hat{\Pi }}_\nabla \) then project to totally geodesic null surfaces for \((c_F,\nabla )\).
A dLp \({\hat{\Pi }}\) for \({{\mathcal {E}}}\) arising in this way for \(d=3,4\) will be called standard. Two dispersionless Lax pairs \({\hat{\Pi }}\), \({\hat{\Pi }}'\) will be called \({{\mathcal {E}}}\)-equivalent, if \({\hat{\Pi }}={\hat{\Pi }}'\) on \({\hat{M}}_u\) for any solution u of \({{\mathcal {E}}}\).
It is an open question in the theory of integrable systems how many non-equivalent coverings a given \({{\mathcal {E}}}\) can possess. Our second result claims that coverings of dLp type are essentially unique under a certain nondegeneracy condition on \({\hat{\Pi }}\). This condition, given in Definition 7 of Sect. 4.5, depends only on \(\Pi ={\hat{\pi }}_*(\Pi )\), implies that \(\Pi \) immerses, and holds in all examples we know of.
The result is straightforward when \(d=4\), but when \(d=3\), it shows that \({\hat{\Pi }}\) can be assumed projective: for some choice of spectral parameter \(\lambda \) and vector fields \(\hat{X},\hat{Y}\) generating \(\hat{\Pi }\), the coefficients of these vector fields are cubic polynomials in \(\lambda \). The result is again not restricted to second order scalar PDEs: we require only that \(\chi ^{{\mathcal {E}}}_{{\varvec{x}}}\) is a nonsingular quadric hypersurface for each \({{\varvec{x}}}\in M_u\).
Theorem 2
Let \({{\mathcal {E}}}: F=0\) be a determined PDE system of order \(\ell \) whose characteristic variety \(\chi ^{{\mathcal {E}}}\) is a bundle of nonsingular quadric hypersurfaces in \({{\mathbb {P}}}(T^*M_u)\). Then any nondegenerate dLp \({\hat{\Pi }}\) is \({{\mathcal {E}}}\)-equivalent to a standard dLp \({\hat{\Pi }}_\nabla \) for some Weyl connection \(\nabla \).
Our third (and main) result establishes an equivalence between the dispersionless integrability of \({{\mathcal {E}}}\) and the EW/SD property of \(c_F\). However, to achieve this, some care is needed in the formulation of both properties. First, in the integrability of the dLp \({\hat{\Pi }}\), we must account for \({{\mathcal {E}}}\)-equivalence. Thus we say that \({{\mathcal {E}}}\) is integrable by a dLp \({\hat{\Pi }}\) if for any \({\hat{\Pi }}'\), which is \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\), the Frobenius integrability condition for \({\hat{\Pi }}'\) is a nontrivial differential corollary of \({{\mathcal {E}}}\). Secondly, the EW/SD property should be a nontrivial differential corollary of \({{\mathcal {E}}}\). The need for nontriviality here is illustrated by PDEs of the form \(\Delta u=f({{\varvec{x}}},u,\partial u)\): this is non-integrable for generic f, but its conformal structure is independent of u and is flat, so the EW/SD property holds automatically. For more general PDE systems \({{\mathcal {E}}}\), a differential corollary of \({{\mathcal {E}}}\) holds nontrivially if it is not a consequence of a proper subsystem \({{\mathcal {E}}}'\) of \({{\mathcal {E}}}\). We can now obtain the main result as follows.
Theorem 3
Let \({{\mathcal {E}}}:F=0\) be a determined PDE system in 3D or 4D whose characteristic variety \(\chi ^{{\mathcal {E}}}\) is a bundle of nonsingular quadric hypersurfaces, for instance a nondegenerate hyperbolic second order scalar PDE (1). Let \(c_F\) be the corresponding conformal structure. Then \({{\mathcal {E}}}\) is integrable by a nondegenerate dLp if and only if
-
3D:
the Einstein–Weyl property for \(c_F\) holds nontrivially on solutions of \({{\mathcal {E}}}\);
-
4D:
the self-duality property for \(c_F\) holds nontrivially on solutions of \({{\mathcal {E}}}\).
Proof
As a preliminary, note that if F has order \(\ell \), then \(c_F\) depends pointwise only on derivatives of u of order \(\leqslant \ell \) (or \(\leqslant (\ell -1)\) if F is quasilinear) and so is defined and is nondegenerate for almost any u (not necessarily a solution). Thus \({\hat{\Pi }}_\nabla \) is defined for any Weyl connection \(\nabla \) over an open subset of \(M_u\), and its integrability there is equivalent to the EW condition for \((c_F,\nabla )\) when \(d=3\) and the SD condition for \(c_F\) when \(d=4\).
Suppose first that \({\hat{\Pi }}\subseteq T{\hat{M}}_u\) is a dLp for \({{\mathcal {E}}}\). By Theorem 1, \(\Pi ={\hat{\pi }}_*({\hat{\Pi }})\) is characteristic, i.e., when \(F=0\), \(\Pi \) is coisotropic for the conformal structure \(c_F\) (and for \(d=4\) we orient \(M_u\) so that \(\Pi \) is a congruence of \(\alpha \)-planes). Nondegeneracy of \({\hat{\Pi }}\) implies that \(\Pi \) immerses into \(\mathop {\mathrm {Gr}}\nolimits _2(TM_u)\) and so we may assume that \({\hat{M}}_u\) is an open subset of the bundle of coisotropic 2-planes for all solutions u, and hence also on an open neighbourhood of \(({{\varvec{x}}},u)\) where \(c_F\) is nondegenerate. Then by Theorem 2, \({\hat{\Pi }}\) is \({{\mathcal {E}}}\)-equivalent to a standard dLp \({\hat{\Pi }}_\nabla \) over any open subset of \(M_u\). Hence the EW/SD condition is a nontrivial differential corollary of \({{\mathcal {E}}}\), as required.
Conversely, suppose that the EW/SD condition is a nontrivial differential corollary of \({{\mathcal {E}}}\) (for some Weyl connection \(\nabla \) when \(d=3\)), and let \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) be the bundle of null 2-planes for \(d=3\), or the bundle of \(\alpha \)-planes for \(d=4\). Then if \({\hat{\Pi }}\) is \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}_\nabla \) (for any Weyl connection \(\nabla \) when \(d=4\)) on an open subset of \(M_u\), the integrability of \({\hat{\Pi }}\) is a differential corollary of \({{\mathcal {E}}}\) on that open subset (since this is true for \({\hat{\Pi }}_\nabla \)).
Finally if any such \({\hat{\Pi }}\) is a differential corollary of a proper subsystem \({{\mathcal {E}}}'\) of \({{\mathcal {E}}}\), then the first part of the argument implies that the EW/SD property is also a consequence of \({{\mathcal {E}}}'\), contradicting nontriviality. \(\quad \square \)
Remark 1
Often, in the physics literature, little distinction is made between a system \({{\mathcal {E}}}\) and a system \({{\mathcal {E}}}'\) obtained by differentiation or potentiation of \({{\mathcal {E}}}\). While some properties of the equation can change, for instance the symmetry algebra and dimension of the solution space, the characteristic variety and integrability of \({{\mathcal {E}}}\) are unaltered. It is easy to adjust the formulation of the theorems to such variations between \({{\mathcal {E}}}\) and \({{\mathcal {E}}}'\).
This theorem shows that the EW and SD equations are master equations, in 3D and 4D respectively, for determined integrable PDE systems whose characteristic variety is a bundle of nonsingular quadric hypersurfaces. It applies in particular to first order systems and higher order scalar equations whose (principal) symbol is a power of a nondegenerate quadratic form. However, the EW and SD equations are not themselves determined systems because of the gauge freedom coming from diffeomorphism invariance. Determined forms of the EW and SD equations were derived in [12], where it was shown in particular that the Manakov–Santini system [24] is equivalent to a determined form of the EW equation. Because of their importance, we will present novel derivations of these determined master equations using the methods of this paper.
Theorem 3 is useful for at least two reasons. First, the geometric characterizations of integrability are algorithmic. In 4D, the anti-self-dual part of the Weyl tensor of \(c_F\) on \(M_u\) can be computed explicitly from finitely many derivatives of u, and so we can check whether it vanishes on solutions by imposing the equation and its prolongations formally—we do not have to be able to resolve the PDE or even to prove its solvability. In 3D, the situation is complicated slightly by the choice of Weyl connection. For the classes of translation-invariant equations considered in [17], there is a universal formula for the Weyl connection, but this formula is not generally applicable (it is not contact-invariant). Nevertheless, except in degenerate situations, the choice is uniquely determined by finitely many derivatives of \(c_F\), and so the EW condition may again be verified by formally imposing the PDE on a tensor depending on finitely many derivatives of u. This effective integrability criterion has many applications: for instance, it was applied in [23] to obtain infinitely many new integrable equations in 4D as deformations of integrable Monge-Ampère equations of Hirota type.
Secondly, the EW/SD property provides a canonical characteristic Lax pair, which, if the PDE on u has order \(\ell \), depends on at most \(\ell +1\) derivatives of u (\(\ell \) if the PDE is quasilinear), and satisfies a ‘normality’ condition off shell which is useful in computations. None of these properties were assumed a priori. For example, the standard Lax pair [24] for the Manakov–Santini system is not normal, and the normal Lax pair may be understood as a Lax pair for an equivalent PDE system presented in [12], which we also discuss.
Apart from the Manakov–Santini system (and variants), Theorem 3 encompasses many examples in 3D, such as the Lax pairs arising in the central quadric ansatz [15], for EW manifolds in diagonal coordinates [12], and for the systems of two first order PDE on two unknown functions studied in [7]. In 4D, there are Lax pairs having no derivatives with respect to the spectral parameter \(\lambda \), which cannot be normal, such as the hypercomplex Lax pair of Dunajski and Joyce (see [2, 12]) and Lax pairs for Monge-Ampère equations of Hirota type [6] as well as systems of Chasles type [8]. However, normal Lax pairs are always available, and provide a canonical choice in 4D, while in 3D they are given by a choice of Weyl connection.
We begin the body of the paper in Sect. 2 by presenting a rigorous definition of what should be called a (nondegenerate) dispersionless Lax pair, motivated by examples. The search for such formalism in general has a long history: see [3, 25] for discussion in the dispersive context. A fundamental role is played by the \(\lambda \)-dependent family \(\Pi ={\hat{\pi }}_*({\hat{\Pi }})\) of rank 2 subbundles of \(TM_u\), which we call a 2-plane congruence. We also explain the normality condition mentioned above, observing that in 4D it determines \({\hat{\Pi }}\) from \(\Pi \).
In Sect. 3, we prove Theorem 1. Here we treat the symbol and characteristic variety of general PDE systems. For both this, and the proof of Theorem 2, we require some jet theory, which we have generally suppressed in the rest of the paper, cf. Remark 2. Having proven Theorem 1, as an addendum, we show in Sect. 3.3 that a Lax pair which is characteristic for a quadric is nondegenerate, and give a computational criterion for the existence of such a quadric for nondegenerate Lax pairs.
For PDE systems whose characteristic variety is a quadric, Theorem 1 shows that \(\Pi \) is essentially unique, which considerably constrains the choice of \({\hat{\Pi }}\), especially in 4D. In 3D, however, more work is needed to prove Theorem 2, which we develop in Sect. 4. We first discuss the standard EW/SD Lax pairs, which are not only normal, but projective. We also introduce and motivate a stronger nondegeneracy condition on the Lax pair \({\hat{\Pi }}\). Roughly speaking, this condition means that the equation \({{\mathcal {E}}}\) appears nontrivially in the symbol of the integrability condition for \({\hat{\Pi }}\) (i.e., at highest order). From this we deduce the projective property of the Lax pair, and hence prove Theorem 2.
In Sect. 5 we discuss applications and extensions of the viewpoint we have developed. In particular, we discuss pseudopotentials and their relation to contact coverings, the twistor interpretation of this relationship, and potential generalizations of the theory.
2 Lax Pairs: Nondegeneracy and Normalization
2.1 Dispersionless pairs and 2-plane congruences
We begin with a well-known prototypical example.
Example 1
(dKP) The dispersionless Kadomtsev–Petviashvilli (dKP) equation (see for example [14]) is the second order scalar PDE
for a scalar function u on a 3-manifold \(M_u\simeq M\) with coordinates (x, y, t). (This differs from some standard conventions by the interchange \(t\leftrightarrow x\) and/or \(u\mapsto -u\).) The dKP equation is the compatibility condition \(\psi _{xy}=\psi _{yx}\) of the first order linear system
for a scalar function \(\psi \) on \({\hat{M}}_u= M_u\times {{\mathbb {R}}}\) with coordinates \((x,y,t,\lambda )\). It may also be described as the compatibility condition \(q_{xy}=q_{yx}\) for the quasilinear system
for a scalar function \(q=q(x,y,t)\) on \(M_u\). In more geometric terms, \(\psi \) is a function on \({\hat{M}}_u\) which is invariant under the vector fields
while q defines a section of \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) such that \({\hat{X}}\) and \({\hat{Y}}\) are tangent to its image. The compatibility condition in either case is that \({\hat{X}}\) and \({\hat{Y}}\) span a distribution \({\hat{\Pi }}\subseteq T{\hat{M}}_u\) which is (Frobenius) integrable, i.e., \([{\hat{X}},{\hat{Y}}]\) is also section of \({\hat{\Pi }}\). In this example, the Frobenius integrability condition holds if and only if \([{\hat{X}},{\hat{Y}}]=0\) if and only if (2) is satisfied.
In this paper, we take the distribution \({\hat{\Pi }}\) on \({\hat{M}}_u\) to be the fundamental object.
Definition 1
A dispersionless pair of order \(\leqslant N\) is a bundle \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) called the correspondence space, whose fibres are connected curves, together with a rank two distribution \({\hat{\Pi }}\subseteq T{\hat{M}}_u\) such that:
-
for all \({\hat{{{\varvec{x}}}}}\in {\hat{M}}_u\), \({\hat{\Pi }}_{{\hat{{{\varvec{x}}}}}}\subseteq T_{{\hat{{{\varvec{x}}}}}} \hat{M}_u\) depends on u only through its partial derivatives at \({{\varvec{x}}}={\hat{\pi }}({\hat{{{\varvec{x}}}}})\in M_u\) of order \(\leqslant N\);
-
\({\hat{\Pi }}\) is transverse to the fibres of \({\hat{\pi }}\), i.e., \({\hat{\Pi }}\cap \ker {\hat{\pi }}_*=0\).
A spectral parameter is a local fibre coordinate \(\lambda =\lambda ({\hat{{{\varvec{x}}}}}):{\hat{M}}_u\rightarrow {{\mathbb {R}}}\) on \({\hat{M}}_u\).
If \({\hat{\Pi }}=\langle {\hat{X}},{\hat{Y}}\rangle \), we thus obtain a first order linear system
for functions \(\psi \) on \({\hat{M}}_u\). In terms of a spectral parameter \(\lambda \), a section of \({\hat{\pi }}\) has image \(\lambda =q({{\varvec{x}}})\) for a function \(q:M_u\rightarrow {{\mathbb {R}}}\), and the corresponding first order quasilinear system is given by
The system (4) is compatible if and only if (5) is compatible if and only if the distribution \({\hat{\Pi }}\) is integrable. Then solutions of (4) and (5) describe respectively functions and hypersurfaces in the (local) leaf space of the folation tangent to \({\hat{\Pi }}\) (the twistor or minitwistor space). The integrability condition of \({\hat{\Pi }}\) is a PDE on u of order \(\leqslant N+1\). Roughly speaking—see Definition 5—dispersionless integrable systems are PDEs arising as such integrability conditions.
We need not restrict attention to scalar PDEs. Indeed we wish to encompass the following important system due to Manakov and Santini [24].
Example 2
(MS) The Manakov–Santini (MS) system is the second order coupled system of PDEs
for functions (u, v) of (x, y, t), where
(As with the dKP equation, we have aligned our coordinate conventions for consistency within this paper. Conventions in the literature [12, 24, 28] vary, but are all equivalent to the one here by point transformations.)
As noted in [24], system (6) is the Frobenius integrability condition for the dispersionless pair \({\hat{\Pi }}=\langle {\hat{X}},{\hat{Y}}\rangle \) spanned by
The corresponding quasilinear covering system, which was studied in [28] and more recently in [32], is
When \(v=0\), the MS system reduces to the dKP equation, and (8) to (3). When \(u=0\), the dLp (8) has no derivatives with respect to the spectral parameter.
If \({\hat{\Pi }}\) is a dispersionless pair, then \(\Pi := {\hat{\pi }}_*({\hat{\Pi }})\) is a rank 2 subbundle of \({\hat{\pi }}^*TM_u\), so at each \({{\varvec{x}}}\in M_u\), we have a 1-parameter family of 2-dimensional subspaces of \(T_{{\varvec{x}}}M\).
Definition 2
A 2-plane congruence \(\Pi \) over \(M_u\) is a section \(\Pi :{\hat{M}}_u\rightarrow {\hat{\pi }}^*\mathop {\mathrm {Gr}}\nolimits _2(TM_u)\), where \(\mathop {\mathrm {Gr}}\nolimits _2(TM_u)\rightarrow M_u\) is the bundle whose fibre over \({{\varvec{x}}}\in M_u\) is the grassmannian of 2-dimensional vector subspaces of \(T_{{\varvec{x}}}M_u\).
Conversely, the passage from a 2-plane congruence \(\Pi \) to a dispersionless pair \({\hat{\Pi }}\) can be understood as a lift with respect to the projection \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\). It is convenient to describe the lift condition in terms of the rank 3 distribution \(\Delta ={\hat{\pi }}_*^{-1}(\Pi )\subseteq T{\hat{M}}_u\): \({\hat{\Pi }}\) is a lift of \(\Pi \) if and only if it is a rank 2 subbundle of \(\Delta \) transverse to the fibres of \({\hat{\pi }}\). For any distributions \(D_1,D_2\subseteq T{\hat{M}}_u\) we denote by \([D_1,D_2]\) the distribution generated by Lie brackets of sections of \(D_1\) and \(D_2\). Thus the integrability condition for \({\hat{\Pi }}\) is that its derived distribution \([{\hat{\Pi }},{\hat{\Pi }}]\) is equal to \({\hat{\Pi }}\).
More explicitly, we choose a spectral parameter \(\lambda \) and let X, Y be linearly independent \(\lambda \)-parametric vector fields on \(M_u\) depending at each \({{\varvec{x}}}\) only on the partial derivatives of u at \({{\varvec{x}}}\) of order \(\leqslant N\). Then \(\Pi =\langle X,Y\rangle \) is a 2-plane congruence, and \(\Delta \) is the span of the coordinate lifts of X, Y (still denoted X, Y, with \(X(\lambda )=0=Y(\lambda )\)) and \(\partial _\lambda \). Then we write a dispersionless pair \({\hat{\Pi }}\) on \({\hat{M}}_u\), with \({\hat{\pi }}_*({\hat{\Pi }})=\Pi \) as the span \({\hat{\Pi }}=\langle {\hat{X}},{\hat{Y}}\rangle \) of vector fields
with \({\hat{\pi }}_*({\hat{X}})=X\) and \({\hat{\pi }}_*({\hat{Y}})=Y\), where m, n are functions of \({{\varvec{x}}}\), u, and the spectral parameter \(\lambda \). The derived distribution of \({\hat{\Pi }}\) is now \([{\hat{\Pi }},{\hat{\Pi }}]=\langle {\hat{X}},{\hat{Y}},[{\hat{X}},{\hat{Y}}]\rangle \subseteq T{\hat{M}}_u\), which generically has rank 3, and the integrability condition is that it has rank 2.
In 3D, we may introduce coordinates (x, y, t) and choose generators of \(\Pi \) of the form
where the functions \(\alpha ,\beta \) depend on (x, y, t), u and \(\lambda \). Dually, the annihilator \(\mathop {\mathrm {Ann}}\nolimits (\Pi )\) of \(\Pi \) in \({\hat{\pi }}^* T^*M_u\) is spanned by the \(\lambda \)-dependent 1-form

\(\mathop {\mathrm {Ann}}\nolimits (\Delta )\) is spanned by the pullback of \(\theta \) to \({\hat{M}}_u\) (which we still denote by \(\theta \)), while \(\mathop {\mathrm {Ann}}\nolimits ({\hat{\Pi }})\) is spanned by \(\theta \) and the 1-form

on \({\hat{M}}_u\). Hence \({\hat{\Pi }}\) is the radical of the 2-form  .
.
In 4D, we similarly may assume that we have coordinates (x, y, z, t) and generators
where \(\alpha ,\beta ,\gamma ,\delta \) depend on (x, y, z, t), u and \(\lambda \). Thus \(\mathop {\mathrm {Ann}}\nolimits (\Pi )\) is spanned by

\(\mathop {\mathrm {Ann}}\nolimits (\Delta )\) by their pullbacks, and \(\mathop {\mathrm {Ann}}\nolimits ({\hat{\Pi }})=\langle \zeta ,\theta ,\eta \rangle \) with \(\eta \) given by (12). In both 3D and 4D, with \({\hat{X}}\) and \({\hat{Y}}\) given by (9), \({\hat{\Pi }}\) is integrable if and only if \([{\hat{X}},{\hat{Y}}]=0\).
2.2 Normality and nondegeneracy
In order for \({\hat{\Pi }}\) to be a dispersionless Lax pair for an equation \({{\mathcal {E}}}: F=0\), we require that the integrability condition \([{\hat{\Pi }},{\hat{\Pi }}]={\hat{\Pi }}\) holds modulo \({{\mathcal {E}}}\), i.e., when \(F=0\) or, to use physics terminology, on shell.
Definition 3
We say that the dispersionless pair \({\hat{\Pi }}\subseteq T{\hat{M}}_u\) is normal if \([{\hat{\Pi }},{\hat{\Pi }}]\subseteq \Delta \) off shell, i.e., without assuming \(F=0\). In other words, \({\hat{\pi }}_*([{\hat{\Pi }},{\hat{\Pi }}])=\Pi \).
If \({\hat{\Pi }}=\langle {\hat{X}},{\hat{Y}}\rangle \) with \({\hat{X}}\) and \({\hat{Y}}\) defined by (9), (10) and (13), then \({\hat{\Pi }}\) is normal if and only if \([{\hat{X}},{\hat{Y}}]\) is a multiple of \(\partial _\lambda \). In this case the integrability condition reduces to the vanishing of the \(\partial _\lambda \)-component \({\hat{X}}(n)-{\hat{Y}}(m)\) of the vector field \([{\hat{X}},{\hat{Y}}]\) (identically in \(\lambda \)).
When \(d=4\), a generic 2-plane congruence \(\Pi \) has a unique normal lift. Indeed, generically, \(\Delta \) is nonholonomic with \([\Delta ,\Delta ]=T{\hat{M}}_u\), i.e., it has the growth vector (3, 5), and following Cartan [4, §11], there is a unique rank 2 subbundle \(\hat{\Pi }\subseteq \Delta \) with \([\hat{\Pi },\hat{\Pi }]=\Delta \). Such rank 2 distribution \(\hat{\Pi }\) either has the growth vector (2, 3, 5) or is integrable. The former case corresponds to Cartan’s celebrated Pfaffian system [4] (for nonintegrable systems or off shell), the latter case corresponds to a dispersionless Lax pair (on shell).
The genericity condition we need here is as follows (and we formulate a similar condition for \(d=3\) which we will use later).
Definition 4
A 2-plane congruence \(\Pi \) is called nondegenerate if

These conditions depend only on \(\Pi \), not on the choices of \(\theta \) or \(\zeta \): when \(d=4\) nondegeneracy means equivalently  where
where  , or dually that
, or dually that  , where \(\Pi =\langle X,Y\rangle \). If we choose \(\theta \) and \(\zeta \) as in (11) and (14), then the nondegeneracy conditions may be written explicitly as:
, where \(\Pi =\langle X,Y\rangle \). If we choose \(\theta \) and \(\zeta \) as in (11) and (14), then the nondegeneracy conditions may be written explicitly as:
Lemma 1
For \(d=4\), any nondegenerate 2-plane congruence \(\Pi \) has a unique normal lift.
Proof
If \({\hat{X}}\) and \({\hat{Y}}\) are given by (9) and (13),  identically, while
identically, while  form two linear equations on m, n:
form two linear equations on m, n:
these have a unique solution by the nondegeneracy condition (17). \(\quad \square \)
Example 3
(SDM) We illustrate this with the master equation for SD structures obtained in [12, Theorem 2]. Consider a 2-plane congruence \(\Pi \) spanned by (13) with \(\alpha _\lambda =0=\delta _\lambda \) and \(\beta _\lambda =1=-\gamma _\lambda \). This is totally isotropic for the conformal class of the metric

which is independent of \(\lambda \). In particular, there is a foliation by the totally isotropic level surfaces of (x, y). Any SD metric can be written in this form, with the isotropic surface foliation being anti-self-dual [12, 31]. The unique normal lift of \(\Pi \) is given by (9) with
Now the \(\lambda ^2\) term of the integrability condition \({\hat{X}}(n)-{\hat{Y}}(m)=0\) is \((\alpha _z+\gamma _t)_z+(\beta _z+\delta _t)_t=0\), so \(\alpha _z+\gamma _t=s_t\) and \(\beta _z+\delta _t=-s_z\) for some function s. However, we may use the translation freedom in \(\lambda \) to set \(s=0\), so that \(\alpha =u_t\), \(\gamma =-(\lambda +u_z)\), \(\beta =\lambda -v_t\), \(\delta =v_z\) for functions (u, v) of (x, y, z, t). Thus we obtain a normal dispersionless pair \({\hat{\Pi }}=\langle {\hat{X}},{\hat{Y}}\rangle \) with
The corresponding quasilinear system (5) is
and the integrability condition reduces to \(X(Q(v))+Y(Q(u))=0\), i.e.,
Up to some minor coordinate changes, this is the SD master equation (SDM) of [12].
2.3 Integrability, dispersionless Lax pairs and normalization
When \(d=3\), we do not obtain a unique normal lift.
Example 4
(MS) The dispersionless pair (8) for the Manakov–Santini system (6) satisfies
with \(F=S(u)+u_t^2\), \(G=S(v)\), and so is not normal. However, if we set \({\hat{X}}'={\hat{X}}-G\,\partial _\lambda \) then \({\hat{X}}'={\hat{X}}\) on shell (when \(F=G=0\)), while
so \({\hat{\Pi }}':=\langle {\hat{X}}',{\hat{Y}}\rangle \) is normal, and is integrable if and only if
i.e., \(G=\psi (x,y)\) and \(F=\psi _y\). However, this system is not substantively different from the Manakov–Santini system itself, because we can make a point transformation \(u\mapsto u-\phi _y(x,y)\), \(v\mapsto v-\phi (x,y)\) and if \(\phi _{yy}=\psi \), we obtain \(F=0\), \(G=0\).
This example illustrates two important issues that we want to incorporate into the definition of a dispersionless Lax pair \({\hat{\Pi }}\) for an equation \({{\mathcal {E}}}\): first \({\hat{\Pi }}\) is only determined modulo \({{\mathcal {E}}}\), and secondly it can be too restrictive in examples to require that the integrability conditions for a dispersionless pair are equivalent to \({{\mathcal {E}}}\).
Definition 5
Let \({{\mathcal {E}}}:F=0\) be a PDE system on u and \({\hat{\Pi }}\subseteq T{\hat{M}}_u\) a dispersionless pair.
-
A dispersionless pair \({\hat{\Pi }}'\subseteq T{\hat{M}}_u\) is \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\) if \({\hat{\Pi }}={\hat{\Pi }}'\) when \(F(u)=0\).
-
\({\hat{\Pi }}\) is a dispersionless Lax pair (dLp) for \({{\mathcal {E}}}\) if for any \({\hat{\Pi }}'\) \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\), the integrability condition \([{\hat{\Pi }}',{\hat{\Pi }}']= {\hat{\Pi }}'\) is a nontrivial differential corollary of \({{\mathcal {E}}}\).
To make precise the notion of a differential corollary, we introduce some jet formalism, for which we refer to [21, 22, 36] for further details. A scalar PDE of order \(\ell \) on a manifold M may be defined as an equation of the form
where \(F\in C^\infty (J^\ell M)\) is a function on the bundle \(\pi _\ell :J^\ell M\rightarrow M\) of \(\ell \)-jets of functions u on M, and \(j^\ell u:M\rightarrow J^\ell M\) is the \(\ell \)-jet of u, i.e., in coordinates \(j^\ell u=({{\varvec{x}}},u,\partial u,\ldots \partial ^\ell u)\).
In order to discuss objects (such as dLps) depending on an arbitrary finite jet of u, we use the infinite jet bundle \(\pi _\infty :J^\infty M\rightarrow M\) which is the union (inverse limit) of \(J^k M\) over all k. A function \(f:J^\infty M\rightarrow {{\mathbb {R}}}\) is smooth if it is the pullback of a function on \(J^k M\) for some \(k\in {{\mathbb {N}}}\), in which case we say f has order \(\leqslant k\). A choice of coordinates \(x^i\) on M leads to coordinates \((x^i,u_\alpha )\) on \(J^\infty M\), where \(1\leqslant i\leqslant d\) and \(\alpha \) runs over all symmetric multi-indices in d entries. Then \(f\in C^\infty (J^\infty M)\) has order \(\leqslant k\) iff it is a function of \(x^i\) and \(u_\alpha \) for all i and \(\alpha =(i_1,\ldots i_j)\) with \(|\alpha |=j\leqslant k\).
The bundle \(J^\infty M\) has a canonical flat connection, the Cartan distribution, for which the horizontal lift of a vector field X on M is the total derivative \(D_X\) characterized by \((D_X f)\circ j^\infty u = X (f\circ j^\infty u)\) for any smooth function f on \(J^\infty M\). More generally, any section X of \(\pi _\infty ^* TM\) has a lift to a vector field \(D_X\) on \(J^\infty M\), given in local coordinates by \(D_X=\sum _i a_iD_i\), where \(X=\sum _i a_i \partial _i\) and \(D_i=\partial _i+\sum _\alpha u_{i\alpha } \partial _{u_\alpha }\).
Higher order operators \(\Box \) in total derivatives (also known as \({{\mathscr {C}}}\)-differential operators) are generated as compositions of the derivations \(D_X\) with coefficients being smooth functions on \(J^\infty M\). In local coordinates, \(\Box =\sum a_\alpha D_\alpha \), where \(a_\alpha \in C^\infty (J^\infty M)\) and \(D_\alpha =D_{i_1}\cdots D_{i_j}\) for a multi-index \(\alpha =(i_1,\ldots i_j)\) with entries in \(\{1,2,\ldots d\}\).
Let \({{\mathcal {I}}}_F\) be the ideal in \(C^\infty (J^\infty M)\) generated by the pullback of \(F\in C^\infty (J^\ell M)\) and its total derivatives of arbitrary order. Then the zero-set \({{\mathcal {E}}}_\infty \subseteq J^\infty M\) of \({{\mathcal {I}}}_F\) is the space of formal solutions of (20): u is a solution of (20) iff \(j^\infty u\) is a section of \({{\mathcal {E}}}_\infty \).
These notions extend straightforwardly to PDE systems by replacing \(J^\infty M\) with the bundle \(\pi _\infty :J^\infty (M,{{\mathcal {V}}})\rightarrow M\) of jets of sections of a fibre bundle \({{\mathcal {V}}}\rightarrow M\), and F by a function of order \(\leqslant \ell \) on \(J^\infty (M,{{\mathcal {V}}})\) with values in a vector bundle \({{\mathcal {W}}}\rightarrow M\). The ideal \({{\mathcal {I}}}_F\) in \(C^\infty (J^\infty (M,{{\mathcal {V}}}))\) is now generated by the components of F and their total derivatives of arbitrary order.
In this formalism, a differential corollary of \({{\mathcal {E}}}:F=0\) is a subset of \({{\mathcal {I}}}_F\) (or, more invariantly, the ideal \({{\mathcal {I}}}\subseteq {{\mathcal {I}}}_F\) generated by this subset and its total derivatives of arbitrary order). It is nontrivial provided it is not a subset of \({{\mathcal {I}}}_{F'}\) for any \(F'\) whose zero-set in \(J^\ell (M,{{\mathcal {V}}})\) contains the zero-set of F as a proper (closed) subset. For example, the ideal generated by \(u_{xy}\), for a scalar function u(x, y, t), is not nontrivial as a differential corollary of the system \(F(j^1u):=(u_x,u_y)=0\), because it is a differential corollary of the equation \(F'(j^1u):=u_x=0\) properly containing the zero-set of F. On the other hand, the equation \(u_{xy}=0\) is a nontrivial differential corollary of the equation \(u_x=0\).
Consequently, in Definition 5, the integrability condition for a dLp \({\hat{\Pi }}\) for \({{\mathcal {E}}}:F=0\) need not generate \({{\mathcal {I}}}_F\): indeed, the freedom to replace a dLp by an \({{\mathcal {E}}}\)-equivalent one may change the ideal \({{\mathcal {I}}}\subseteq {{\mathcal {I}}}_F\) that its integrability conditions generate.
Remark 2
In most of the paper we make minimal use of the jet formalism by using the philosophy [21, 36] that a differential equation \({{\mathcal {E}}}_\infty \subseteq J^\infty M\) is a generalized manifold whose “points” are solutions u, identified with \(M_u=(j^\infty u)(M)\subseteq {{\mathcal {E}}}_\infty \) that is diffeomorphic to M via \(\pi _\infty \). We are justified in working “pointwise” provided there are enough “points” (i.e., for generic \(u_\infty \in {{\mathcal {E}}}_\infty \) there is a solution u with \(u_\infty \in M_u\)), and there are existence theorems for hyperbolic PDEs (or rather, ultrahyperbolic PDEs in signature (2, 2)) which assert this in some generality. Nevertheless, we would rather not rely upon such analytical results here, and all our results can be formalized using jets, even if we do not do so explicitly.
The following normalization result now suffices to establish Theorem 2 when \(d=4\).
Proposition 1
Let \({\hat{\Pi }}\) be a dLp such that \(\Pi ={\hat{\pi }}_*({\hat{\Pi }})\) is nondegenerate. Then \({\hat{\Pi }}\) is \({{\mathcal {E}}}\)-equivalent to a normal dLp. Such a Lax pair for \(d=4\) is unique.
Proof
When \(d=4\) the Lax pair condition (on shell) implies

for some operators \(\Box _1,\Box _2\) in total derivatives. Let us modify \({\tilde{X}}={\hat{X}}+A(F)\partial _\lambda \), \({\tilde{Y}}={\hat{Y}}+B(F)\partial _\lambda \), where A, B are operators in total derivatives to be determined (they also depend on \(\lambda \)). The new commutation equation is

Vanishing of these, equivalent to normality, can be achieved by a unique choice of the operators in total derivatives A, B due to nondegeneracy condition (17).
When \(d=3\), the Lax pair condition (on shell) implies similarly

for some operator \(\Box \) in total derivatives. The modification \(\tilde{X}={\hat{X}}+A(F)\partial _\lambda \), \({\tilde{Y}}={\hat{Y}}+B(F)\partial _\lambda \) gives the new commutation relations

The equation \(\beta _\lambda A-\alpha _\lambda B=\Box \) admits the solution \(A=\alpha _{\lambda \lambda }\Box /(\beta _\lambda \alpha _{\lambda \lambda }-\alpha _\lambda \beta _{\lambda \lambda })\) and \(B=\beta _{\lambda \lambda }\Box /(\beta _\lambda \alpha _{\lambda \lambda }-\alpha _\lambda \beta _{\lambda \lambda })\) by (16), unique up to the freedom \((A,B)\mapsto (A,B)+(\alpha _\lambda ,\beta _\lambda )L\).
\(\square \)
3 The Characteristic Condition for Dispersionless Lax Pairs
3.1 Symbols and the characteristic condition
In order to prove Theorem 1 in full generality, we need the notions of symbol and characteristic variety for a general PDE system. For this we use the jet formalism. Recall from the previous section that a smooth function F on \(J^\infty M\) has order \(\leqslant \ell \) if it is a pullback from \(J^\ell M\), and that \(J^\infty M\) has a canonical connection, the Cartan distribution. The vertical part of the 1-form  may be viewed in coordinates as a polynomial on \(\pi _\infty ^* T^*M\) given by
may be viewed in coordinates as a polynomial on \(\pi _\infty ^* T^*M\) given by
The top degree term \(\sigma _F=F_{(\ell )}\), called the (order \(\ell \)) symbol of F, is independent of coordinates. We assume it is nonvanishing: if it vanishes, F has order \(\leqslant \ell -1\) and \(\sigma _F\) has lower degree.
This generalizes to a PDE system of order \(\ell \), i.e., a function F of order \(\leqslant \ell \) on \(J^\infty (M,{{\mathcal {V}}})\), for some fibre bundle \({{\mathcal {V}}}\), with values in a vector bundle \({{\mathcal {W}}}\rightarrow M\). The symbol \(\sigma _F\) of F is then a homogeneous degree \(\ell \) polynomial on \(\pi _\infty ^*T^*M\) with values in \(\mathop {\mathrm {Hom}}\nolimits (T{{\mathcal {V}}},{{\mathcal {W}}})\), which we assume is not identically zero, so that the PDE system does not have order \(\leqslant \ell -1\). The characteristic variety of the PDE system \({{\mathcal {E}}}:F=0\) is defined by [34]
If \({{\mathcal {V}}}\) and \({{\mathcal {W}}}\) have the same rank, then \([\theta ]\) is characteristic iff \(\sigma _F(\theta )\) is not surjective. We take \(\mathop {\mathrm {rank}}\nolimits ({{\mathcal {V}}})=\mathop {\mathrm {rank}}\nolimits ({{\mathcal {W}}})\) as the definition of a determined system, although a more proper definition is \(\mathop {\mathrm {codim}}\nolimits \chi ^{{\mathcal {E}}}=1\).
Definition 6
We say that a 2-plane congruence \(\Pi \) (or a dLp \({\hat{\Pi }}\)) is characteristic for \({{\mathcal {E}}}\) if for any solution u of \({{\mathcal {E}}}\) and any \(\theta \) in \(\mathop {\mathrm {Ann}}\nolimits (\Pi )\subseteq {\hat{\pi }}^*T^*M_u\), we have \([\theta ]\in \chi ^{{\mathcal {E}}}\).
In the jet formalism, a dispersionless pair \({\hat{\Pi }}\) lives on a rank 1-bundle \({\hat{\pi }}:{\hat{M}} \rightarrow J^\infty (M,{{\mathcal {V}}})\) (so that \({\hat{M}}_u=(j^\infty u)^*{\hat{M}}\)) and we let \({\hat{\pi }}_\infty =\pi _\infty \circ {\hat{\pi }} :{\hat{M}}\rightarrow M\). A 2-plane congruence \(\Pi \) is then a rank 2 subbundle of \({\hat{\pi }}_\infty ^* TM\), and \({\hat{\Pi }}\) is a lift of \(\Pi \) to \(T{\hat{M}}\). In practice we use a spectral parameter \(\lambda \) to trivialize \({\hat{M}}\) over \(J^\infty (M,{{\mathcal {V}}})\). Then \(T{\hat{M}}\) is the direct sum of the vertical bundle of \({\hat{\pi }}\), spanned by \(\partial _\lambda \), and \({\hat{\pi }}^* TJ^\infty (M,{{\mathcal {V}}})\). Thus if \(\Pi \) is spanned by \(X,Y\in {\hat{\pi }}_\infty ^* TM\), we may write the dispersionless pair \({\hat{\Pi }}\) as the span of \({\hat{X}} = D_X + m\,\partial _\lambda \) and \({\hat{Y}}= D_Y+ n\,\partial _\lambda \), where \(D_X\) and \(D_Y\) are total derivatives (depending also on \(\lambda \)) and m, n are functions on \({\hat{M}}\). Then
The integrability condition \([{\hat{X}},{\hat{Y}}]\in \Gamma ({\hat{\Pi }})\) reduces to \([X,Y] + m\,\partial _\lambda Y -n\,\partial _\lambda X=\nu _X\, X+\nu _Y\, Y\), for some \(\nu _X,\nu _Y\), together with the vanishing of \(D_X n - D_Y m + m\,\partial _\lambda n - n\,\partial _\lambda m-\nu _X\, m-\nu _Y\, n\). As in the previous section, we may choose X and Y so that \(\nu _X=\nu _Y=0\), and hence the Lax equation (split into the vertical and horizontal parts) becomes the system
We thus have a dLp for \({{\mathcal {E}}}\) if these equations hold modulo \({{\mathcal {I}}}_F\) i.e., all components (and hence their total derivatives of arbitrary order) belong to \({{\mathcal {I}}}_F\).
Lemma 2
If \(D_X q - D_Y p\) has order \(\leqslant k\), for functions p, q of \(u_\infty \in J^\infty (M,{{\mathcal {V}}})\) and sections X, Y of \(\pi _\infty ^* TM\), then its order k symbol is

If X, Y are linearly independent, and \(P_1\) and \(P_2\) are symmetric k-vectors with  , there is a symmetric \((k-1)\)-vector S with
, there is a symmetric \((k-1)\)-vector S with  and
and  .
.
Proof
Equation (23) is straightforward from the definition of the total derivative and the product rule for the vertical differentiation. Extending X, Y pointwise to a basis, the second part reduces to the trivial observation that for any homogeneous polynomials \(P_j=P_j(\xi _1,\ldots \xi _d)\), \(j=1,2\), with \(\xi _1 P_2=\xi _2 P_1\), there is a homogeneous polynomial P with \(P_j=\xi _j P\). \(\quad \square \)
Lemma 3
Let (21)–(22) have order \(\leqslant k+1\) modulo \({{\mathcal {I}}}_F\), i.e., all their higher symbols vanish modulo \({{\mathcal {I}}}_F\). Then there is a symmetric k-tensor \(S_k\) and a symmetric TM-valued k-tensor \(Q_k\) such that, modulo \({{\mathcal {I}}}_F\), the order \(k+1\) symbols of (21) and (22) are respectively


Proof
Suppose that X, Y, m, n depend only on the N-jet of u for some \(N\in {{\mathbb {N}}}\), so that (21)–(22) have order \(\leqslant N+1\), and it suffices to prove the lemma for \(k\leqslant N\). We thus induct on \(p=N-k\). For \(p=0\), the order \(k+1=N+1\) symbols of (21) and (22) are simply \(X\odot n_{(k)} - Y\odot m_{(k)}\) and \(X\odot Y_{(k)} - Y\odot X_{(k)}\) by (23), so we are done, with \(S_k=0=Q_k\).
Now suppose that the lemma holds with \(k=N-p\) for some \(p\geqslant 0\), and suppose that (21)–(22) have order \(\leqslant k\) modulo \({{\mathcal {I}}}_F\). Then (21) certainly has order \(\leqslant k+1\) modulo \({{\mathcal {I}}}_F\), and so the inductive hypothesis implies its order \(k+1\) symbol, which vanishes modulo \({{\mathcal {I}}}_F\), is given by (24). Hence Lemma 2 produces a symmetric \((k-1)\)-tensor \(S_{k-1}\) such that, modulo \({{\mathcal {I}}}_F\),

Similarly, by (25), there is a symmetric TM-valued \((k-1)\)-tensor \(Q_{k-1}\) such that

modulo \({{\mathcal {I}}}_F\). By (23), the order k symbol of (21) is

Hence, substituting for \(X_{(k)}, Y_{(k)}, m_{(k)}, n_{(k)}\), we have

A lot of cancellation now occurs to leave

and the last two lines vanish modulo \({{\mathcal {I}}}_F\), which establishes (24) for \(k'=N-(p+1)=k-1\). We turn now to the order k symbol of (22), which, by (23), is

Hence, substituting for \(X_{(k)}, Y_{(k)}, m_{(k)}, n_{(k)}\), we have, modulo \({{\mathcal {I}}}_F\),

and the last two lines again vanish modulo \({{\mathcal {I}}}_F\), so that (25) holds for \(k'=N-(p+1)=k-1\), completing the proof. \(\quad \square \)
3.2 Proof of Theorem 1
The characteristic property depends only on the dispersionless pair \({\hat{\Pi }}\) up to \({{\mathcal {E}}}\)-equivalence, so the strategy is to take \({\hat{\Pi }}\) to have integrability condition of minimal order within its \({{\mathcal {E}}}\)-equivalence class.
As above, we let \({{\mathcal {I}}}_F\) be the ideal generated by F and its total derivatives, and assume that \({\hat{\Pi }}\) is spanned by vector fields \(D_X+m\,\partial _\lambda \) and \(D_Y+n\,\partial _\lambda \) which commute on shell, where X, Y, m, n depend only on the N-jet of u for some \(N\in {{\mathbb {N}}}\).
By the definition of a dLp, equations (21)–(22) have the form \(\Lambda _1(F)=0\) and \(\Lambda _2(F)=0\), where \(\Lambda _1\) and \(\Lambda _2\) are \(\lambda \)-dependent operators in total derivatives on the codomain \({{\mathcal {W}}}\) of F, the latter operator being TM-valued. We suppose that \(\Lambda _1(F)\) and \(\Lambda _2(F)\) both have order \(\leqslant k+1\) modulo \({{\mathcal {I}}}_F\) and that k is minimal with this property among all dispersionless pairs \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\). Note that \(k+1\geqslant \ell \), the order of F.
In local coordinates we may write \(\Lambda _1\) as a finite sum \(\sum _\alpha b_\alpha (u_\infty ,\lambda ) D_\alpha \) where each \(b_\alpha (u_\infty ,\lambda )\) is a section of \({{\mathcal {W}}}^*\). Then for any \(r\geqslant \ell \), the order r symbol of \(\Lambda _1(F)\) satisfies

(using the product rule for vertical differentiation). Let \(r=\max \{|\alpha |:b_\alpha \notin {{\mathcal {I}}}_F\}+\ell \). Then  . Since \(\chi ^{{\mathcal {E}}}\) is (fibrewise) a proper closed variety, \(\sigma _F(\theta )\) is surjective for generic \(\theta \), and by definition of r, there exists such a \(\theta \) with \(\sum _{|\alpha |=r-\ell } \partial _\alpha (\theta )b_\alpha (u_\infty ,\lambda )\notin {{\mathcal {I}}}_F\). Hence \(\Lambda _1(F)_{(r)}(\theta )\notin {{\mathcal {I}}}_F\), and so we must have \(r\leqslant k+1\) because \(\Lambda _1(F)\) has order \(\leqslant k+1\) modulo \({{\mathcal {I}}}_F\).
. Since \(\chi ^{{\mathcal {E}}}\) is (fibrewise) a proper closed variety, \(\sigma _F(\theta )\) is surjective for generic \(\theta \), and by definition of r, there exists such a \(\theta \) with \(\sum _{|\alpha |=r-\ell } \partial _\alpha (\theta )b_\alpha (u_\infty ,\lambda )\notin {{\mathcal {I}}}_F\). Hence \(\Lambda _1(F)_{(r)}(\theta )\notin {{\mathcal {I}}}_F\), and so we must have \(r\leqslant k+1\) because \(\Lambda _1(F)\) has order \(\leqslant k+1\) modulo \({{\mathcal {I}}}_F\).
Thus for all \(|\alpha |\ge k-\ell +2\), we have \(b_\alpha \in {{\mathcal {I}}}_F\) by definition of r, and hence  is a \({{\mathcal {W}}}^*\)-valued symmetric \((k-\ell +1)\)-vector depending on \((u_\infty ,\lambda )\). An analogous argument shows
is a \({{\mathcal {W}}}^*\)-valued symmetric \((k-\ell +1)\)-vector depending on \((u_\infty ,\lambda )\). An analogous argument shows  for a \(TM\otimes {{\mathcal {W}}}^*\)-valued symmetric \((k-\ell +1)\)-vector \(L_2\) depending on \((u_\infty ,\lambda )\).
for a \(TM\otimes {{\mathcal {W}}}^*\)-valued symmetric \((k-\ell +1)\)-vector \(L_2\) depending on \((u_\infty ,\lambda )\).
By Lemma 3, the order \(k+1\) symbols of \(\Lambda _1(F),\Lambda _2(F)\) have the forms (24)–(25) modulo \({{\mathcal {I}}}_F\). Hence, on any solution u we have that for all \(\theta \in \mathop {\mathrm {Ann}}\nolimits (\Pi )\)
(there is only one independent \(\theta \) at each point for \(d=3\) and a pair of such for \(d=4\)).
Suppose for contradiction that \(\sigma _F(\theta )\) is surjective for some \(\theta \in \mathop {\mathrm {Ann}}\nolimits (\Pi )\)—hence almost every such \(\theta \), since surjectivity is an open condition. Then (26) implies on shell that \(L_1(\theta )=0\) and \(L_2(\theta )=0\) identically (as degree \(k+1-\ell \) polynomials) in \(\theta \in \mathop {\mathrm {Ann}}\nolimits (\Pi )\). If \(k+1=\ell \) this immediately yields that \((L_1,L_2)=0\) modulo \({{\mathcal {I}}}_F\), a contradiction. For \(k\geqslant \ell \) we have instead  and
and  modulo \({{\mathcal {I}}}_F\) for some symmetric \((k-\ell )\)-vectors \(T_1,U_1\) with values in \({{\mathcal {W}}}^*\) and \(T_2,U_2\) with values in \(TM\otimes {{\mathcal {W}}}^*\).
modulo \({{\mathcal {I}}}_F\) for some symmetric \((k-\ell )\)-vectors \(T_1,U_1\) with values in \({{\mathcal {W}}}^*\) and \(T_2,U_2\) with values in \(TM\otimes {{\mathcal {W}}}^*\).
We now let \(\tau _1,\upsilon _1,\tau _2,\upsilon _2\) be order \(k-\ell \) operators in total derivatives such that \(\tau _1 F\) has order k symbol  modulo \({{\mathcal {I}}}_F\) and so on: concretely, in local coordinates, if \(T_1=\sum _{|\alpha |=k-\ell } t_\alpha (u_\infty ,\lambda ) \partial _\alpha \), we may take \(\tau _1 = \sum _{|\alpha |=k-\ell } t_\alpha (u_\infty ,\lambda ) D_\alpha \). We then modify the dispersionless pair by \(m\mapsto m-\upsilon _1 (F)\), \(n\mapsto n-\tau _1 (F)\), \(X\mapsto X-\upsilon _2 (F)\), \(Y\mapsto Y-\tau _2 (F)\).
modulo \({{\mathcal {I}}}_F\) and so on: concretely, in local coordinates, if \(T_1=\sum _{|\alpha |=k-\ell } t_\alpha (u_\infty ,\lambda ) \partial _\alpha \), we may take \(\tau _1 = \sum _{|\alpha |=k-\ell } t_\alpha (u_\infty ,\lambda ) D_\alpha \). We then modify the dispersionless pair by \(m\mapsto m-\upsilon _1 (F)\), \(n\mapsto n-\tau _1 (F)\), \(X\mapsto X-\upsilon _2 (F)\), \(Y\mapsto Y-\tau _2 (F)\).
This modification is \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\), but the new order \(k+1\) symbols of (21)–(22) vanish modulo \({{\mathcal {I}}}_F\), so they have order \(\leqslant k\) modulo \({{\mathcal {I}}}_F\). This contradicts minimality of k.
Thus \(\sigma _F(\theta )\) is not surjective for any \(\theta \in \mathop {\mathrm {Ann}}\nolimits (\Pi )\). Since the PDE system is determined this implies that \(\theta \) is characteristic, and we are done. \(\quad \square \)
3.3 Dispersionless pairs characteristic for a quadric
If \({\hat{\Pi }}\) is a dLp for an equation \({{\mathcal {E}}}\) whose characteristic variety \(\chi ^{{\mathcal {E}}}\) is a quadric, then \(\Pi \) is coisotropic for this quadric by Theorem 1. In this section we investigate the extent to which \(\Pi \) recovers this quadric. We begin with a uniqueness criterion, and then discuss existence. We make essential use of the nondegeneracy conditions (16)–(17), which imply in particular that at each \({{\varvec{x}}}\in M_u\), the image of \(\Pi _{{\varvec{x}}}:\lambda \mapsto \Pi _{({{\varvec{x}}},\lambda )}\) does not lie in any proper projective linear subspace of  .
.
Proposition 2
If a 2-plane congruence \(\Pi \) is coisotropic for \(c_F\), then for any \({{\varvec{x}}}\in M_u\) and \(\lambda \in {\hat{\pi }}^{-1}({{\varvec{x}}})\) at which \(\Pi _{{\varvec{x}}}\) is an immersion, it is nondegenerate at \({{\varvec{x}}}\). Conversely, at any point \({{\varvec{x}}}\) where \(\Pi \) is nondegenerate, there is at most one (quadratic) conformal structure \(c_F\) on \(T_{{{\varvec{x}}}} M_u\) with \(\Pi _{({{\varvec{x}}},\lambda )}\) coisotropic for all \(\lambda \), and it must be nondegenerate and hyperbolic.
Proof
Suppose first that \(d=3\), so that \(\mathop {\mathrm {Gr}}\nolimits _2(T_{{\varvec{x}}}M_u)\cong {{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\) is a projective plane, and \(\mathop {\mathrm {Ann}}\nolimits (\Pi _{{{\varvec{x}}}})\) is a curve in this plane. If \(\Pi \) is coisotropic, then \(\mathop {\mathrm {Ann}}\nolimits (\Pi _{{{\varvec{x}}}})\) lies on the nonsingular conic \(\{[\theta ]:\sigma _F(\theta )=0\}\) and so if \(\Pi _{{{\varvec{x}}}}\) is immersed, its derivatives of order \(\leqslant 2\) in \(\lambda \) span \({{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\), hence it is nondegenerate. Conversely, two distinct nonsingular conics meet in at most four points, so \(\mathop {\mathrm {Ann}}\nolimits (\Pi _{{{\varvec{x}}}})\) lies on at most one nonsingular conic (which is nonempty, hence hyperbolic), and if \(\mathop {\mathrm {Ann}}\nolimits (\Pi _{{{\varvec{x}}}})\) lies on a singular conic, it lies on a line, hence \(\Pi _{{{\varvec{x}}}}\) is degenerate.
Suppose instead that \(d=4\), so that (the Plücker embedding of) \(\mathop {\mathrm {Gr}}\nolimits _2(T_{{\varvec{x}}}M_u)\) is the Klein quadric in  , and
, and  is a curve in this quadric. If \(\Pi \) is coisotropic, then
is a curve in this quadric. If \(\Pi \) is coisotropic, then  lies in a nondegenerate plane section of this quadric, which is a conic: the corresponding lines in \({{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\) belong to one of the rulings of the quadric surface \(\{[\theta ]:\sigma _F(\theta )=0\}\) in \({{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\). In particular, if \(\Pi _{{{\varvec{x}}}}\) is immersed, its tangent does not lie in the quadric, hence it is nondegenerate. Conversely, two distinct nonsingular quadric surfaces meet in a degree four curve (containing at most four lines), so if \(\Pi _{{\varvec{x}}}\) is nonconstant, it lies on at most one nonsingular quadric surface (which is hyperbolic because it contains lines), and if \(\Pi _{{\varvec{x}}}\) has image in a singular quadric surface, then the lines pass through a point or lie in a plane, hence
lies in a nondegenerate plane section of this quadric, which is a conic: the corresponding lines in \({{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\) belong to one of the rulings of the quadric surface \(\{[\theta ]:\sigma _F(\theta )=0\}\) in \({{\mathbb {P}}}(T^*_{{{\varvec{x}}}}M_u)\). In particular, if \(\Pi _{{{\varvec{x}}}}\) is immersed, its tangent does not lie in the quadric, hence it is nondegenerate. Conversely, two distinct nonsingular quadric surfaces meet in a degree four curve (containing at most four lines), so if \(\Pi _{{\varvec{x}}}\) is nonconstant, it lies on at most one nonsingular quadric surface (which is hyperbolic because it contains lines), and if \(\Pi _{{\varvec{x}}}\) has image in a singular quadric surface, then the lines pass through a point or lie in a plane, hence  lies in a proper projective linear subspace of \(\mathop {\mathrm {Gr}}\nolimits _2(T_{{\varvec{x}}}M_u)\), hence \(\Pi _{{{\varvec{x}}}}\) is degenerate. \(\quad \square \)
lies in a proper projective linear subspace of \(\mathop {\mathrm {Gr}}\nolimits _2(T_{{\varvec{x}}}M_u)\), hence \(\Pi _{{{\varvec{x}}}}\) is degenerate. \(\quad \square \)
Proposition 3
Suppose \(d=3\) and the nondegeneracy condition (16) holds. Then there is a unique conformal structure c for which the 2-plane congruence \(\Pi =\langle X,Y\rangle \) is null for all \(\lambda \) if and only if the Monge invariant \(I(\alpha ,\beta )=0\). This invariant has order 5 in the entries and it distinguishes conics in the projective plane. In the local parametrization with \(\beta =\lambda \), this condition is the following (we denote \(\alpha '=\alpha _\lambda \) etc.):
Suppose \(d=4\) and the nondegeneracy condition (17) holds. Then there is a unique conformal structure c for which the 2-plane congruence \(\Pi =\langle X,Y\rangle \) is (co)isotropic for all \(\lambda \) if and only if the following system of differential equations of order 3 holds, which we write in a partially integrated second order form so (again \(\alpha '=\alpha _\lambda \) etc.)
where \(k_{vw}\) are \(\lambda \)-independent and satisfy the “cocycle conditions” \(k_{vw}+k_{wv}=0\), \(u'k_{vw}+v'k_{wu}+w'k_{uv}=0\) for \(u,v,w\in \{\alpha ,\beta ,\gamma ,\delta \}\). In the normalization \(\delta =\lambda \) these conditions simplify to: \((\alpha ,\beta ,\gamma )''={\mathbf {v}}\, |\alpha '-\beta '\gamma '|^{3/2}\), where \({\mathbf {v}}\) is a \(\lambda \)-independent 3-component vector.
Proof
Let us discuss first the case \(d=3\). We are looking for a conformal structure c, represented by a pseudo-Riemannian metric g of signature (2, 1), such that the planes \(\Pi =\langle X,Y\rangle \) are null. Consider the Pfaffian form  . The null condition is a single equation \(c(\theta ,\theta )=0\). Adding to it its \(\lambda \)-derivatives up to order 4, we get a system of 5 equations on 6 coefficients of the metric (5 coefficients if considered up to proportionality). This system is solvable iff (16) holds. Provided this nondegeneracy condition, we can uniquely find \(c=[g]\), but in order for it to be supported on \(M_u\) (and not on \({\hat{M}}_u\)) the ratio of the coefficients of g must be \(\lambda \)-independent. This is equivalent to the condition \(I(\alpha ,\beta )=0\).
. The null condition is a single equation \(c(\theta ,\theta )=0\). Adding to it its \(\lambda \)-derivatives up to order 4, we get a system of 5 equations on 6 coefficients of the metric (5 coefficients if considered up to proportionality). This system is solvable iff (16) holds. Provided this nondegeneracy condition, we can uniquely find \(c=[g]\), but in order for it to be supported on \(M_u\) (and not on \({\hat{M}}_u\)) the ratio of the coefficients of g must be \(\lambda \)-independent. This is equivalent to the condition \(I(\alpha ,\beta )=0\).
Consider now the case \(d=4\). Add to the 3 equations \(c(X,X)=0\), \(c(X,Y)=0\), \(c(Y,Y)=0\) their first and second derivatives in \(\lambda \). The obtained system of 9 equations on 10 coefficients of the metric (9 coefficients if considered up to proportionality) is solvable iff condition (17) holds. Provided this nondegeneracy condition, we can uniquely find \(c=[g]\), but in order for it to be supported on \(M_u\) (and not on \({\hat{M}}_u\)) the ratio of the coefficients of g must be \(\lambda \)-independent. This is equivalent to the system of equations formulated in the proposition. \(\quad \square \)
4 Projective Dependence on the Spectral Parameter
4.1 Weyl connections and standard dLps
For any 2-plane congruence \(\Pi \) which is characteristic for a bundle of nonsingular quadric hypersurfaces, there is a well-known construction of lifts \({\hat{\Pi }}_\nabla \) of \(\Pi \) from Weyl connections \(\nabla \), i.e., torsion-free connections preserving the conformal structure c defining the quadric. Such Weyl connections form an affine space modelled on the vector space of 1-forms on \(M_u\).
Lemma 4
Let \(\Pi \) be a nondegenerate 2-plane congruence on \({\hat{M}}_u\rightarrow M_u\), characteristic for a bundle of quadric hypersurfaces, and \(\nabla \) a Weyl connection. Then \(\nabla \) induces a connection on \({\hat{M}}_u\) such that the horizontal lift \({\hat{\Pi }}_\nabla \) of \(\Pi \) is normal.
Proof
Since \(\nabla \) is a conformal connection, it induces a connection on the bundle of coisotropic planes for c, and hence on \({\hat{M}}_u\), since \(\Pi \) is an immersion. The pullback of \(\nabla \) to \({\hat{\pi }}^* TM_u\) preserves \(\Pi \) and hence, since \(\nabla \) is torsion-free, the horizontal lift \({\hat{\Pi }}\) satisfies \({\hat{\pi }}_*[{\hat{\Pi }},{\hat{\Pi }}]=\Pi \). \(\quad \square \)
We refer to such a lift \({\hat{\Pi }}_\nabla \) as a standard dLp. For \(d=4\), any standard dLp \({\hat{\Pi }}_\nabla \) is the unique normal lift of \(\Pi ={\hat{\pi }}_*({\hat{\Pi }}_\nabla )\), hence independent of the choice of Weyl connection, as is well known [29]. However, for both \(d=3\) and \(d=4\), standard dLps are very special because the connection induced by \(\nabla \) on \({\hat{M}}_u\) is projective: \({\hat{M}}_u\) is locally isomorphic to a \({{\mathbb {P}}}^1\)-bundle over \(M_u\) and if \(\lambda \) is a spectral parameter induced by an affine coordinate on this projective bundle, then horizontal lifts of (\(\lambda \)-independent) vector fields on \(M_u\) depend quadratically on \(\lambda \) (because vector fields on \({{\mathbb {P}}}^1\) have this form in an affine chart).
Furthermore, with respect to such a projective spectral parameter \(\lambda \), there is a local parametrization of vector fields spanning \(\Pi \) that is linear in \(\lambda \), i.e., \(\Pi =\langle V_1+\lambda V_3,V_2+\lambda V_4\rangle \) for \(\lambda \)-independent vector fields \(V_i\) on \(M_u\), so that their lifts are cubic in \(\lambda \).
When \(d=4\), these properties follow from the existence of an adapted frame \(V_1,V_2,V_3,V_4\) for \(M_u\) such that in the dual coframe \(\theta _1,\theta _2,\theta _3,\theta _4\), the conformal structure is represented by \(g=\theta _1\theta _4-\theta _2\theta _3\). Then (up to a choice of orientation) \(\Pi =\langle V_1+\lambda V_3,V_2+\lambda V_4\rangle \), \(\Delta =\langle V_1+\lambda V_3,V_2+\lambda V_4,\partial _\lambda \rangle \) and it is straightforward to verify that the unique normal lift of \(\Pi \) is
where the coefficients m, n are given in terms of the structure functions \(c_{ij}^k=\theta _k([V_i,V_j])\) of the frame as
These are cubic in \(\lambda \) as required, and compatible with the representation \(m=m_1+\lambda m_3\) and \(n=m_2+\lambda m_4\) for coefficients \(m_i\) of \(\partial _\lambda \) in the lifts of \(V_i\) that are quadratic in \(\lambda \).
When \(d=3\), there is similarly an adapted frame \(V_0,V_1,V_2\) on \(M_u\) with the dual coframe \(\theta _0,\theta _1,\theta _2\) such that conformal structure \(c_F\) is represented by the Lorentzian metric \(g=4\theta _0\theta _2-\theta _1^2\) and \(\Pi =\langle V_0+\lambda V_1,V_1+\lambda V_2\rangle =\ker \theta (\lambda )\), where
for a (projective) spectral parameter \(\lambda \). We then have the following fact (cf. [14]).
Lemma 5
Let \(d=3\) and let \(\Pi \) be as in Lemma 4. Then Weyl connections parametrize projective normal lifts \({\hat{\Pi }}\) of \(\Pi \).
Proof
By definition any projective lift given by (9), with \(X=V_0+\lambda V_1,Y=V_1+\lambda V_2\) affine linear, has m, n cubic in \(\lambda \), i.e., \(m=\sum _{i=0}^3m_i\lambda ^i\), \(n=\sum _{i=0}^3n_i\lambda ^i\). Now \(\mathop {\mathrm {Ann}}\nolimits (\Pi )\) is spanned by the 1-form (27) where \(\theta _i(V_j)=\delta _{ij}\). Hence \(\theta ({\hat{\pi }}_*[{\hat{X}},{\hat{Y}}])= \theta ([X,Y]-nV_1+mV_2)\) is a quartic polynomial in \(\lambda \) determining 5 of the 8 coefficients of m and n. It is straightforward to check that remaining three coefficients are determined uniquely by the Weyl connection (a 1-form has three components at each point). \(\quad \square \)
4.2 The modified Manakov–Santini master equation in 3D
As mentioned in the introduction, the integrability for a standard dLp \({\hat{\Pi }}_\nabla \) in 3D is well-known to be equivalent to the EW equation on \((c,\nabla )\) and has the geometric interpretation that any EW manifold locally admits (many) foliations by totally geodesic null surfaces [5, 19] (corresponding to curves in the minitwistor space). We now use this to obtain an alternative derivation of the Manakov–Santini system [24] as a master equation in 3D, or rather a modification of this system which was previously derived in [12] by a different method.
Any totally geodesic null surface has a canonical foliation by null geodesics, so any EW manifold admits a local coordinate system (x, y, t), where x and y are pulled back from local coordinates on the local leaf spaces of a totally geodesic null surface foliation and the induced null geodesic foliation respectively. Thus \(\partial _t\) is null and orthogonal to \(\partial _y\) and we can use the freedom in the t coordinate so that the conformal structure has a representative metric

for some functions a and b. This has the form \(4\theta _0\theta _2-\theta _1^2\), where  ,
,  is the coframe dual to \(V_0=\partial _x + a \partial _y + b \partial _t\), \(V_1=-\partial _y\) and \(V_2=\partial _t\). Thus the null 2-plane congruence \(\Pi =\langle V_0+\lambda V_1, V_1+\lambda V_2\rangle \) is the kernel of
is the coframe dual to \(V_0=\partial _x + a \partial _y + b \partial _t\), \(V_1=-\partial _y\) and \(V_2=\partial _t\). Thus the null 2-plane congruence \(\Pi =\langle V_0+\lambda V_1, V_1+\lambda V_2\rangle \) is the kernel of

and is equal to \(W_0^\perp \) where
Since \(\partial _y\) and \(\partial _t\) are tangent to level surfaces of x, which are the null surfaces corresponding to \(\lambda =\infty \), the standard dLp must have the form \({\hat{\Pi }}_\nabla =\langle V_0+\lambda V_1+m'\partial _\lambda , V_1+\lambda V_2+n'\partial _\lambda \rangle \) where \(m'\) and \(n'\) are quadratic in \(\lambda \).
To obtain a 2-plane congruence in the form (10), we let \(X= V_0+\lambda V_1 + (a-\lambda )(V_1+\lambda V_2)\) and \(Y=-(V_1+\lambda V_2)\) so that \({\hat{X}}\) and \({\hat{Y}}\) are given by (9) with \(m=m' + (a-\lambda )n'\) and \(n=-n'\). The Lax integrability condition \([{\hat{X}},{\hat{Y}}]=0\) implies \(n'\) is affine linear in \(\lambda \), while \(m'\) is a quadratic in \(\lambda \), where the coefficient h of \(\lambda ^2\) is a function of x and y. We may set h to zero using the coordinate freedom
which preserves the form of \(\theta (\lambda )\) (hence also g) up to rescaling by \(\rho _y(x,y)^2\) and a redefinition of a and b. The Lax equation now implies that the \(\lambda \) coefficient of \(m'\) differs from \(-a_y\) by a function of x and y which may be set to zero using the remaining coordinate freedom
We then find that \(m'=-a_y\lambda -b_y\), \(n'=a_t \lambda + b_t\), and hence
The Lax integrability condition now reduces to the determined system
This is the form of the EW system given in [12, (11)–(12)], except that the x and t variables have been swapped in our conventions and we have used the identity \((aa_y)_t=(aa_t)_y\). Substituting \(a=v_t\) and \(b=u-v_y\) gives the Manakov–Santini system. The modified version (31) may also be written more geometrically as
where \(\Delta ^g\) is the Laplacian of the metric g in (28), and \(\{a,f\}_P = a_y f_t - a_t f_y\) is the Poisson bracket with respect to the bivector field  tangent to the null surface foliation.
tangent to the null surface foliation.
Remark 3
In [12] a translationally noninvariant version of the MS system was also derived and the question of an explicit equivalence to the standard MS system was raised. However, the translationally noninvariant version is obtained from a generic null surface foliation of the EW manifold, and the coordinate transformation to a totally geodesic null surface foliation will be transcendental in general.
4.3 Arbitrary lifts of 2-plane congruences in 3D
We showed in Proposition 1 that any dLp can be made normal. However, when \(d=3\), the normal lift of a 2-plane congruence \(\Pi \) is not unique. Instead, the rank 3 distribution \(\Delta =\hat{\pi }_*^{-1}(\Pi )\subseteq T{\hat{M}}_u\) has a unique Cauchy characteristic: a rank 1 subbundle \({{\mathcal {C}}}\subseteq \Delta \) with \([{{\mathcal {C}}},\Delta ]=\Delta \). For a rank 2 subbundle \(\hat{\Pi }\subseteq \Delta \) the normality condition \([\hat{\Pi },\hat{\Pi }]\subseteq \Delta \) implies that \({{\mathcal {C}}}\subseteq \hat{\Pi }\), but one generator of \({\hat{\Pi }}\) remains undetermined. In the case of interest that \(\Pi =\ker \theta \) is characteristic for a quadric, an easy computation shows that \({{\mathcal {C}}}\) is spanned by the vector field
where, using the structure functions \(c_{ij}^k=\theta _k([V_i,V_j])\) of the adapted frame \(V_0,V_1,V_2\), we have
These formulae are compatible with representation \(\sigma =m_0+2\lambda m_1+\lambda ^2m_2\) for the coefficients \(m_i\) of the lifts of \(V_i\) which we want to show can be chosen quadratic in \(\lambda \).
Without loss of generality we may write \(\hat{\Pi }=\langle \hat{W},\hat{U}\rangle \) with
We also write \(W_2=V_2=(W_1)_\lambda \). The nondegeneracy condition (15) on \(\Pi \) implies that \(W_0,W_1,W_2\) form a (\(\lambda \)-dependent) frame for \(TM_u\) and indeed

is the inverse metric to \(g=4\theta _0\theta _2-\theta _1^2\), which is nondegenerate and independent of \(\lambda \).
The Frobenius integrability condition \([\hat{\Pi },\hat{\Pi }]=\hat{\Pi }\) is the condition that
is a section of \({\hat{\Pi }}\). Identifying \(V_1\equiv -\lambda V_2-\psi \partial _\lambda \), \(V_0\equiv \lambda ^2V_2+(2\lambda \psi -\sigma )\partial _\lambda \) modulo \(\hat{\Pi }\), and assuming that the lift is normal, this reduces to \({{\mathfrak {e}}}=0\), where
Using the coefficients of the decomposition \([W_0,W_1]={\bar{c}}_{01}^0 W_0+{\bar{c}}_{01}^1 W_1+{\bar{c}}_{01}^2 W_2\) we get
Note that \(\deg _\lambda {\bar{c}}_{01}^0=2\), \(\deg _\lambda {\bar{c}}_{01}^1=3\) and \(\deg _\lambda {\bar{c}}_{01}^2=4\).
Example 5
(dKP) For the dKP equation (2), we have  ,
,  and
and
whence \({{\mathfrak {e}}}=\psi _x-2\lambda \psi _y+(\lambda ^2+u)\psi _t+(\lambda u_t-u_y)\psi _\lambda -u_{yy}+2\lambda u_{yt}-\lambda ^2u_{tt}-\psi u_t+2\psi ^2\). In this case, via the change of variables \(\psi =\varphi ^{-1}+u_t\), the equation \({{\mathfrak {e}}}=0\) (34) takes the linear inhomogeneous form
If we assume \(\psi \) either local (\(=\) differential) in u or global (\(=\) algebraic) in \(\lambda \), then the only solution is \(\varphi ^{-1}=0\), implying the existence of a unique dLp (standard) of these types.
However, there exist solutions to (36) which are non-algebraic in \(\lambda \) and nonlocal in u. Indeed for any Cauchy data \(u|_{t=0}\) that is non-algebraic in \(\lambda \), we obtain such a solution. In this way we obtain a (characteristic but not projective or local) Lax pair that does not give rise to an EW structure. Moreover, there is no uniqueness for such Lax pairs.
In the following Sects. 4.4–4.6 we deduce the cubic behaviour of \(\psi \) in \(\lambda \) from the equation \({{\mathfrak {e}}}=0\), a strengthened nondegeneracy condition, and the requirement that the dLp is local in u. This suffices to establish the projective property, and hence Theorem 2.
4.4 Scalar PDEs in 3D
We first consider the case of a scalar differential equation \({{\mathcal {E}}}:F=0\) of order \(\ell \), i.e., one PDE (20) on one function u. As before, we assume that the characteristic variety \(\chi ^{{\mathcal {E}}}\) is a quadric, which implies that \(\ell \) is even and the symbol \(F_{(\ell )}\) of the differential operator is a power of a nondegenerate quadratic form: \(\ell =2m\), \(F_{(\ell )}=Q^m\) for some \(Q\in \Gamma (S^2TM_u)\) on \({{\mathcal {E}}}\). (For a second order scalar PDE (1) we get \(m=1\).) Using the notation of the previous section, we have  .
.
The order of the conformal structure \(c_F\) in u satisfies \(k=\mathop {\mathrm {ord}}\nolimits (c_F)\leqslant \ell \), and the strict inequality is possible, for instance, when F is quasilinear (dKP is an example with \(0=k<\ell =2\)). Then the frame \(V_i\) with the dual coframe \(\theta _i\) can be chosen of the same order k in u, while the structure functions \(c_{\smash {ij}}^t\) and the coefficient \(\sigma \) in (32) have order \(\leqslant k+1\).
Let us suppose \(\hat{\Pi }\) is a normal dLp for \({{\mathcal {E}}}\). We want to find an \({{\mathcal {E}}}\)-equivalent dLp which is projective. Since \({\hat{\Pi }}\) is normal, we may suppose, as in the previous section, that its integrability condition is \({{\mathfrak {e}}}= 0\) with \({{\mathfrak {e}}}\) given by (34). Hence by definition of a dLp, \({\mathfrak {e}}=\Box F\) for some operator \(\Box \) in total derivatives. If \(\psi \) has order \(r\geqslant k+2\) then by taking the \((r+1)\)-symbol of this equation we obtain

and hence conclude (since  is indivisible by \(W_0\)) that the symbol of \(\psi \) is divisible by that of F. Therefore we can modify \(\psi \) off shell (fixed on shell) to obtain an \({{\mathcal {E}}}\)-equivalent dLp in which the new \(\psi \) has order \(<r\). By iterating this process, we may thus assume, up to \({{\mathcal {E}}}\)-equivalence, that \(\psi \) has order \(\leqslant k+1\) from the outset.
is indivisible by \(W_0\)) that the symbol of \(\psi \) is divisible by that of F. Therefore we can modify \(\psi \) off shell (fixed on shell) to obtain an \({{\mathcal {E}}}\)-equivalent dLp in which the new \(\psi \) has order \(<r\). By iterating this process, we may thus assume, up to \({{\mathcal {E}}}\)-equivalence, that \(\psi \) has order \(\leqslant k+1\) from the outset.
The \((k+2)\)-symbol of \({{\mathfrak {e}}}=\Box F\) now yields, using equation (34), the relation

for a section \(R\in \Gamma (S^{k-2m+2}TM_u)\) of the bundle of homogeneous degree \(k-2m+2\) polynomials on \(T^*M_u\), i.e., \(R=\sum _{|\tau |=k-2m+2}a_\tau W_\tau \), where we let  for a multi-index \(\tau =(j_1\cdots j_t)\) of length \(|\tau |=t\). By modification of \(\psi \) and \(\sigma \) off shell, we can bring this function modulo \({{\mathcal {I}}}_F\) to the form
for a multi-index \(\tau =(j_1\cdots j_t)\) of length \(|\tau |=t\). By modification of \(\psi \) and \(\sigma \) off shell, we can bring this function modulo \({{\mathcal {I}}}_F\) to the form
(indeed, all terms of R with \(W_0\) factor can be absorbed into \(\psi _{(k+1)}\), while those with \(W_1\) factor into \(\sigma _{(k+1)}\); this absorption is identical on shell). Formula (37) then implies that

for some \(T\in \Gamma (S^kTM_u)\), and by the normalization (38), the coefficients for R and T are uniquely determined by independent components of \(\sigma \) and hence they are polynomial in \(\lambda \). In particular, since \(\sigma \) is a quartic polynomial in \(\lambda \), we conclude that \(\mu \in C^\infty (J^{k+1}M_u)\) is a polynomial in \(\lambda \) with \(\deg _\lambda \mu \leqslant 3\).
Also, T is a polynomial in \(\lambda \) with \(\deg _\lambda T\leqslant 2\). Therefore, \(\psi _{(k+1)}\) is a cubic polynomial in \(\lambda \). Thus, there exists a function \(\psi _1=\psi _1(\partial ^{k+1}u,\lambda )\) with \(\deg _\lambda \psi _1\leqslant 3\) such that \(\psi _0:=\psi -\psi _1\) has order \(\leqslant k\) in u. Substituting \(\psi =\psi _1+\psi _0\) into the equation \({{\mathfrak {e}}}=\Box F\) we get
where \(\tilde{q}_1=q_1+4\psi _1\), while \(\tilde{q}_0\) is a expression of order \(k+1\) in u that we do not write explicitly. However, it follows from (35) that \(\tilde{q}_1,\tilde{q}_0\) are polynomial in \(\lambda \) with \(\deg _\lambda \tilde{q}_1\leqslant 3\), \(\deg _\lambda \tilde{q}_0\leqslant 8\). We now want to show that \(\psi _0\) is also polynomial in \(\lambda \).
In order to do this, it is convenient to carry out computations in the nonholonomic \(\lambda \)-dependent frame \((W_i)_{i=0}^2\) rather than the holonomic frame \((\partial _{x^i})_{i=0}^2\) induced by local coordinates \((x^i)_{i=0}^2\) on \(M_u\). Let \((a_i^j)\) be the transition matrix between these frames and \((b_i^j)\) be its inverse, i.e., \(W_i=a_i^j\partial _{x^j}\) and \(\partial _{x^i}=b_i^jW_j\) (summation convention). These vector fields induce vertical vector fields \({\mathbb {D}}_{W_\tau }\) on jets via the formulae \({\mathbb {D}}_{W_\tau }=b_{j_1}^{i_1}\cdots b_{j_t}^{i_t}\partial _{u_{i_1\cdots i_t}}\), where \(\tau =(j_1,\ldots j_t)\). If \(\xi \) is a function on the jet bundle (i.e., a differential operator) with order t symbol \(\xi _{(t)}\), then \({\mathbb {D}}_{W_\tau }\xi \), with \(|\tau |=t\), is the the coefficient \(\xi _t^\tau \) of \(\xi _{(t)}\) in the decomposition \(\xi _{(t)}=\xi _t^{\rho } W_\rho \) (summation over multi-indices \(\rho \) with \(|\rho |=t\)).
Next, since the dual co-frame to \((W_0,W_1,W_2)\) is \((\frac{1}{2}\theta _{\lambda \lambda },-\theta _\lambda ,\theta )\), the coefficients on the right hand sides of identities (35) may be written
This and formula (39) lead to
To obtain the last formula note that we have \({\mathbb {D}}_{W_1^aW_2^b}[W_0,W_1]=-{\mathbb {D}}_{W_1^{a-1}W_2^b}W_0\) from the definition of the commutator. Then apply this to the identity \(\sigma =-\theta ([W_0,W_1])\) and the first formula for \(\mu \).
Identity (39) yields \(\theta ({\mathbb {D}}_{W_1^rW_2^{k-r}}W_0)=0\) unless \(r=2m-2\). Note that by (39) we have  , and this decomposition can be refined:
, and this decomposition can be refined:

where \(\gamma ={\mathbb {D}}_{W_1^{2m-2}W_2^{k-2m+2}}(T) =\theta \bigl ({\mathbb {D}}_{W_0W_1^{2m-3}W_2^{k-2m+2}}(W_0)\bigr ) -\theta \bigl ({\mathbb {D}}_{W_1^{2m-2}W_2^{k-2m+2}}(W_1)\bigr )\) and by dots we mean all terms with other \(W_\tau \) that are irrelevant for the computation. Consequently,

and since \(\sigma _\lambda =(\theta [W_1,W_0])_\lambda =\theta _\lambda [W_1,W_0]+\theta [W_2,W_0] ={\bar{c}}_{01}^1-\theta [W_0,W_2]\) we get

Thus from (35) we get the following expression for the \((k+1)\)-symbol

Taking now \((k+1)\)-symbol of (40), we get

Denoting  and extracting the coefficients at the indicated terms (which are unchanged by \({{\mathcal {E}}}\)-equivalence) we obtain the following system
and extracting the coefficients at the indicated terms (which are unchanged by \({{\mathcal {E}}}\)-equivalence) we obtain the following system
All coefficients of this linear system on \(\psi _0\) are polynomials in \(\lambda \). We assume \(\mu \ne 0\) (this condition will be discussed in the next section). Then the first equation uniquely determines \(\psi _0\). Moreover, \(\mu \) divides \(\kappa _0\) as a polynomial in \(\lambda \) because otherwise \(\psi _0\) is a proper rational function and then the second equation, written as \((\psi _0\mu ^{-2})_\lambda =\kappa _1\mu ^{-3}\), yields a contradiction.
Thus \(\psi _0\), and hence also \(\psi \), are polynomials in \(\lambda \), and \(\deg _\lambda \psi \leqslant 5\). Since the parameter \(\lambda \) is manifestly projective, a projective change should not destroy the polynomial property. Using the special projective transformation \(\lambda \mapsto \lambda ^{-1}\) (or a similar projective transformation arbitrarily close to the identity), we conclude that in fact \(\deg _\lambda \psi \leqslant 3\).
Moreover, the function \(\psi \) should be compatible with \(\sigma \) in the sense that \(\psi =m_1+\lambda m_2\), \(\sigma =m_0+2\lambda m_1+\lambda ^2m_2\) for some \(\lambda \)-quadrics \(m_i\). This will be derived from the cubic property of \(\psi \) in the general case in Sect. 4.6.
4.5 Nondegeneracy for scalar and vector equations
The \(\lambda \)-dependent quantity \(\mu \) introduced in (41) characterizes the extent to which the Lax integrability condition depends on the equation \({{\mathcal {E}}}\). If this condition does not involve F and its derivatives, the dLp is trivial (holds off shell). We require that the equation enters on the level of the top symbol, i.e., \((k+1)\)-jet, or equivalently that \(\mu \ne 0\). We first observe that this condition is invariant under admissible transformations of \({\hat{M}}_u\) as a \({{\mathbb {P}}}^1\)-bundle over \(M_u\).
Proposition 4
The scalar quantity \(\mu \) is a relative differential invariant, i.e., transforms by a nonvanishing scalar multiple under admissible transformations.
Proof
The admissible transformations of \({\hat{M}}_u\) have the form \(({{\varvec{x}}},\lambda )\mapsto (\Phi ({{\varvec{x}}}),\Psi ({{\varvec{x}}},\lambda ))\), where \(\Phi \) is a conformal transformation of \((M_u,[g])\) and \(\Psi ({{\varvec{x}}},\lambda )=\frac{a({{\varvec{x}}})+b({{\varvec{x}}})\lambda }{c({{\varvec{x}}})+d({{\varvec{x}}})\lambda }\) is a parametric Möbius transformation. These preserve the algebraic behaviour of the dLp \(\hat{\Pi }\), and a straightforward computation shows they scale \(\mu \) by a nonvanishing scalar multiple.
Alternatively, using the framework and normalizations of Sect. 4.4, \(\sigma \) given by (32) is independent of the adapted frame up to scale and the leading coefficient of its symbol \({\mathbb {D}}_{W_1^{2m-1}W_2^{k-2m+2}}(\sigma )\) is a relative invariant, as required. \(\quad \square \)
Let us now give the vector version, recalling the set-up. In this case \(F:J^\ell (M,{{\mathcal {V}}})\rightarrow {{\mathcal {W}}}\) is a determined (nonlinear) differential operator of order \(\ell \) on sections \({{\varvec{u}}}\) of a fibre bundle \({{\mathcal {V}}}\) over \(M_u\) with values in a rank s vector bundle \({{\mathcal {W}}}\). We assume, for simplicity, that \({{\mathcal {V}}}\) is also a vector bundle of rank s so that we can identify the vertical bundle \(T_{{\varvec{u}}}^{\mathrm{v}}{{\mathcal {V}}}\) along a section \({{\varvec{u}}}\) with \({{\mathcal {V}}}\). Locally, in coordinates, F has components \(F^i\) that are scalar differential operators of order \(\ell \) on vector-function \({{\varvec{u}}}=(u^j)\) of \({{\varvec{x}}}\), where \(i,j\in \{1,\ldots s\}\).
The symbol of F at \({{\varvec{u}}}=(u^i)\) is a map \(F_{(\ell )}:S^\ell T^*M_{{\varvec{u}}}\otimes {{\mathcal {V}}}\rightarrow {{\mathcal {W}}}\) that we identify with an \(s\times s\) matrix \({{\varvec{F}}}=(F_i^j)\), whose coefficients are polynomials of degree \(\ell \) on \(T^*M_{{\varvec{u}}}\). Similarly, the symbol of a scalar differential operator \(\varphi \) can be identified with a column in components. The characteristic variety \(\chi ^{{\mathcal {E}}}\) of \({{\mathcal {E}}}\) is a quadric if \(\det ({{\varvec{F}}})=Q^m\) as before.
The setup of the previous section extends, and \(\mu =\theta \bigl ({\mathbb {D}}_{W_1^{2m-2}W_2^{k-2m+2}}(W_0)\bigr )\) is a section of the bundle \({{\mathcal {V}}}\) over \(M_u\) for solutions u of the vector version of (20). The following statement is proved similarly to Proposition 4.
Proposition 5
The section \(\mu \) is a relative differential invariant, i.e., under admissible transformations it is mapped to another section related to \(\mu \) by an automorphism of the bundle \({{\mathcal {V}}}\). Hence the (non-)vanishing of \(\mu \) is an invariant property.
Note that \(\mu \) depends not on a lift or dLp but only on the equation \({{\mathcal {E}}}:F=0\) itself.
Definition 7
In 3D the equation is called nondegenerate (and its dLp nontrivial) if the relative invariant \(\mu \) is nonzero (identically in \(\lambda \)).
This condition is trivially satisfied if the conformal structure \(c_F\) has zero order in u, as happens in the dKP case. It can be proved for several classes of PDE in 3D (with \(\mathop {\mathrm {ord}}\nolimits _u(c_F)>0\)), and we do not know of any integrable equation violating this condition.
Remark 4
In fact, the Manakov–Santini equation, which by [12] is the master equation for EW geometry, is nondegenerate in the sense of this definition. We check this for the modified version, with \(W_0\) given by (30). Since order of the conformal structure in this formalism is \(k=0\), and also \(m=1\), we compute the symbol of \(W_0\) by (a, b) as \((\partial _t,\partial _y)\) and applying \(\theta \) given by (29) we get \(\mu =(\lambda ,1)\ne 0\). Thus the MS equation is nondegenerate and we adopt this condition for our main result.
4.6 Proof of Theorem 2
Any nondegenerate dLp \({\hat{\Pi }}\) is \({{\mathcal {E}}}\)-equivalent to a normal dLp by Proposition 1. When \(d=4\), the normal dLp has the projective property, while for \(d=3\), the main task is to show that, up to \({{\mathcal {E}}}\)-equivalence, we may assume that \(\psi \) in (33) is cubic in \(\lambda \). The proof almost directly generalizes the scalar version of Sect. 4.4, so we only indicate important differences on each step.
-
(i)
We begin with equation \({{\mathfrak {e}}}=\Box F\) and, as before, by an off shell modification can arrange that \(\mathop {\mathrm {ord}}\nolimits \psi \leqslant k+1\), where k is the order of the conformal structure \(c_F\). Then its \((k+2)\)-symbol and (34) yield the following matrix equation
 (42)
(42)where \(\psi ^i\) are components of the symbol \(\psi _{(k+1)}\) and similarly for \(\sigma \), and where \(R^i\) are the symbols of some operators in total derivatives. Multiplying this equation by the adjugate matrix \(\mathop {\mathrm {adj}}\nolimits ({{\varvec{F}}})\) (which satisfies \(\mathop {\mathrm {adj}}\nolimits ({{\varvec{F}}}){{\varvec{F}}}=\det ({{\varvec{F}}})I=Q^m I\)) and denoting the rows of the resulting left-hand side matrix \([{\tilde{\psi }}^i\ {\tilde{\sigma }}^i]\) we get the equations

from which we obtain a vector analogue of equation (39) for each component \(i\in \{1,\ldots s\}\). Moreover, we can obtain normalization analogues \(R_i=(-1)^{m-1}\mu _i\, W_2^{k-2m+2}\) of (38). This implies that \({\tilde{\psi }}^i\) and hence \(\psi ^i\) can be chosen polynomial in \(\lambda \), moreover \(\deg _\lambda \psi ^i\leqslant 3\).
-
(ii)
Thus there exist a decomposition \(\psi =\psi _1+\psi _0\), where \(\psi _1\) is at most cubic in \(\lambda \) and has \((k+1)\)-symbol \((\psi ^i)\) at \({{\varvec{u}}}=(u^j)\), while \(\psi _0\) has order \(\leqslant k\). Substituting this into the constraint \({\mathfrak {e}}=\Box F\) we obtain a vector analogue of equation (40). Taking its \((k+1)\)-symbol and applying \(\mathop {\mathrm {adj}}\nolimits ({{\varvec{F}}})\) again gives
$$\begin{aligned} \tilde{q}_1{\!}^i\psi _0+\tilde{\sigma }^i\partial _\lambda \psi _0=\tilde{q}_0{\!}^i,\qquad i\in \{1,\ldots s\}. \end{aligned}$$If \(\mu =(\mu _1,\ldots \mu _s)\) is nonzero (identically in \(\lambda \)), we conclude by the same argument that \(\psi _0\) is polynomial in \(\lambda \) with \(\deg \psi _0\leqslant 5\). Hence \(\psi \) is a polynomial in \(\lambda \) with \(\deg \psi \leqslant 5\).
-
(iii)
If the coefficients of \(\psi \) at \(\lambda ^4\) or \(\lambda ^5\) are nonzero, then a Möbius transformation \(\lambda \mapsto \frac{a({{\varvec{x}}})+b({{\varvec{x}}})\lambda }{c({{\varvec{x}}})+d({{\varvec{x}}})\lambda }\) arbitrary close to the identity maps the system of vector fields \(\hat{W}\) and \(\hat{U}=V_1+\lambda V_2+\psi \partial _\lambda \) (after taking a proper linear combination and clearing denominators) to a system of the same form with a new \(\psi \) of higher degree. Thus we must have \(\deg _\lambda \psi \leqslant 3\), which is a projectively invariant property.
-
(iv)
In addition to \(\hat{U}\) the vector field \(\hat{W}-\lambda \hat{U}=V_0+\lambda V_1+(\sigma -\lambda \psi )\partial _\lambda \) have degree \(\leqslant 3\) in \(\lambda \). Indeed, under a change of the adapted frame \((V_0,V_1,V_2)\) and a projective change of parameter \(\lambda \) this field becomes of the form \(\hat{U}\) and so the claim follows from (i)–(iii).
-
(v)
Note that the frame \(V_0,V_1,V_2\) is arbitrary subject to the condition that
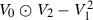 is conformal to the inverse metric. In particular, \(V_1+\lambda V_2+\psi \partial _\lambda \) has cubic coefficient of \(\partial _\lambda \) for arbitrary non-null \(V_1\) and null \(V_2\). Changing the pair \((V_1,V_2)\) to the pair \((-V_1,V_2)\) and subtracting the results we get that the lift of \(V_1\) has cubic coefficient of \(\partial _\lambda \). Here \(V_1\) is arbitrary non-null vector. Applying a similar argument to \(V_0+\lambda V_1+(\sigma -\lambda \psi )\partial _\lambda \) from (iv) we obtain that the coefficient of \(\partial _\lambda \) in the lift of arbitrary null vector \(V_0\) is also at most cubic in \(\lambda \).
is conformal to the inverse metric. In particular, \(V_1+\lambda V_2+\psi \partial _\lambda \) has cubic coefficient of \(\partial _\lambda \) for arbitrary non-null \(V_1\) and null \(V_2\). Changing the pair \((V_1,V_2)\) to the pair \((-V_1,V_2)\) and subtracting the results we get that the lift of \(V_1\) has cubic coefficient of \(\partial _\lambda \). Here \(V_1\) is arbitrary non-null vector. Applying a similar argument to \(V_0+\lambda V_1+(\sigma -\lambda \psi )\partial _\lambda \) from (iv) we obtain that the coefficient of \(\partial _\lambda \) in the lift of arbitrary null vector \(V_0\) is also at most cubic in \(\lambda \).Now the property of being cubic in \(\lambda \) for the coefficient of \(\partial _\lambda \) of the lift of a \(\lambda \)-independent vector is not projectivelly invariant, while the entire construction is projectively invariant. Therefore the coefficient of \(\partial _\lambda \) in the lift of arbitrary vector is actually quadratic.
Theorem 2 is now immediate. By Lemma 5 normal lifts with this projective property are bijective with Weyl connections for \(d=3\), while for \(d=4\) the normal lift is unique by Lemma 1. Thus for \(d=3\) or \(d=4\), the standard Lax pair of \((M_u,c_F,\nabla )\) or \((M_u,c_F)\) is \({{\mathcal {E}}}\)-equivalent to \({\hat{\Pi }}\). \(\quad \square \)
5 Applications and Generalizations
5.1 Pseudopotentials
In this paper we have defined dispersionless integrable systems using a Lax pair of vector fields. In 3D, an alternative approach relies instead on pseudopotentials or nonlinear dispersionless Lax pairs, cf. [17, 27, 38].
Definition 8
A pseudopotential for a PDE \(F=0\) is a function \(S:M_u\rightarrow {{\mathbb {R}}}\) whose derivative  satisfies an overdetermined system of two equations that are compatible on shell, i.e., when \(F(j^\ell u)=0\).
satisfies an overdetermined system of two equations that are compatible on shell, i.e., when \(F(j^\ell u)=0\).
Locally, in coordinates (x, y, t), we may write these equations as \(S_x=A(S_t)\) and \(S_y=B(S_t)\) where A and B also depend on (x, y, t). If they depend on (x, y, t) (only or also) through a section v of a vector bundle over \(M_u\), and the integrability condition \(\partial _y(A(S_t))=\partial _x(B(S_t))\) is required to hold identically in \(S_t\), we obtain a PDE system on v. Dispersionless integrable systems are often defined as those determined PDEs arising in this way.
More invariantly, the two equations determine a codimension two (hence 4-dimensional) submanifold N of the cotangent bundle \(T^*M_u\) and S is a pseudopotential with respect to these equations if  takes values in N. The integrability condition means that N is coisotropic for the canonical symplectic form \(\Omega \) on \(T^*M_u\). Here we recall that
takes values in N. The integrability condition means that N is coisotropic for the canonical symplectic form \(\Omega \) on \(T^*M_u\). Here we recall that  where \(\tau \) is the tautological 1-form on \(T^*M_u\) (with \(\beta ^*\tau =\beta \) for any 1-form \(\beta \) on \(M_u\)). The coisotropic condition means that the pullback of \(\Omega \) to N has rank two, hence a 2-dimensional radical (or kernel).
where \(\tau \) is the tautological 1-form on \(T^*M_u\) (with \(\beta ^*\tau =\beta \) for any 1-form \(\beta \) on \(M_u\)). The coisotropic condition means that the pullback of \(\Omega \) to N has rank two, hence a 2-dimensional radical (or kernel).
Locally N is a fibre bundle over \(M_u\) and we may take \(\lambda =S_t\) as a fibre coordinate in the above explicit formulation. Thus
and so the integrability condition is
where \(\{A,B\}_P\) is the Poisson bracket of A and B with respect to the Poisson structure  ; equivalently, the vector fields
; equivalently, the vector fields  and
and  commute, where
commute, where  and
and  are the hamiltonian vector fields associated to A and B by the Poisson structure P (cf. e.g. [13]).
are the hamiltonian vector fields associated to A and B by the Poisson structure P (cf. e.g. [13]).
Alternatively, if (43) holds, then the pullback of \(\Omega \) to N is

and its radical is the dLp spanned by  and
and  .
.
Conversely, let \({\hat{\Pi }}\) be a dLp on \({\hat{\pi }}:{\hat{M}}_u \rightarrow M_u\). On shell, \({\hat{\Pi }}\) is integrable and so \({\hat{M}}\) fibres locally over a minitwistor space \({{\mathcal {T}}\!w}\) [19]. At least locally \({{\mathcal {T}}\!w}\) admits a nondegenerate (and necessarily closed) 2-form (such as  in local coordinates); this then pulls back to a closed 2-form \(\omega \) on \({\hat{M}}_u\) with radical \({\hat{\Pi }}\). We may therefore write (locally, on shell)
in local coordinates); this then pulls back to a closed 2-form \(\omega \) on \({\hat{M}}_u\) with radical \({\hat{\Pi }}\). We may therefore write (locally, on shell)  for a 1-form \(\alpha \) on \({\hat{M}}_u\), which we may assume vanishes on the fibres of \({\hat{M}}_u\) over \(M_u\); hence we may write
for a 1-form \(\alpha \) on \({\hat{M}}_u\), which we may assume vanishes on the fibres of \({\hat{M}}_u\) over \(M_u\); hence we may write  for a section
for a section  of \({\hat{\pi }}^*T^*M_u = \{({\hat{p}},\xi )\in {\hat{M}}_u\times T^*M_u\,|\, \xi \in T^*_{{\hat{\pi }}({\hat{p}})} M_u\}\). Then \({\tilde{\alpha }}:{\hat{M}}_u\rightarrow T^*M_u\) is an immersion whose image is coisotropic, since \({\tilde{\alpha }}^*\tau =\alpha \) and so
of \({\hat{\pi }}^*T^*M_u = \{({\hat{p}},\xi )\in {\hat{M}}_u\times T^*M_u\,|\, \xi \in T^*_{{\hat{\pi }}({\hat{p}})} M_u\}\). Then \({\tilde{\alpha }}:{\hat{M}}_u\rightarrow T^*M_u\) is an immersion whose image is coisotropic, since \({\tilde{\alpha }}^*\tau =\alpha \) and so  has rank two with radical \({\hat{\Pi }}\).
has rank two with radical \({\hat{\Pi }}\).
In order to do this off shell, we have to work modulo the PDE system. However, the construction of the coisotropic immersion \({\tilde{\alpha }}\) from a dLp requires integration, and so it may be necessary to pass to a covering system.
Example 6
(dKP) We illustrate this with the well-known example of the dKP equation (2) \((u_x + u u_t)_t = u_{yy}\) with dLp (3). We must now find a function f so that  is closed modulo the equation, and then a 1-form \(\alpha \) such that
is closed modulo the equation, and then a 1-form \(\alpha \) such that  modulo the equation. For the first step, it happens in this case that \(f=1\) works. For the second, setting
modulo the equation. For the first step, it happens in this case that \(f=1\) works. For the second, setting

we have that  modulo the covering system \(v_t=u_y\) and \(v_y=u_x + u u_t\). Thus the pseudopotential system is \(S_x=\frac{1}{3} S_t^3 - u S_t - v\) and \(S_y=\frac{1}{2} S_t^2 - u\).
modulo the covering system \(v_t=u_y\) and \(v_y=u_x + u u_t\). Thus the pseudopotential system is \(S_x=\frac{1}{3} S_t^3 - u S_t - v\) and \(S_y=\frac{1}{2} S_t^2 - u\).
Note that the above nonlocality (usage of v) may be avoided by using the potential form \(u_{xt}+u_t u_{tt}-u_{yy}=0\) of dKP. In this case the pseudopotential S is given by the equations: \(S_x=\lambda ^3/3-u_t\lambda -u_y\), \(S_y=\lambda ^2/2-u_t\), \(S_t=\lambda \). In both cases the parameter \(\lambda \) is aligned to the Lax pair in the sense that it is the projective parameter on the correspondence bundle \({\hat{M}}_u\rightarrow M_u\). This is no longer so with Manakov–Santini system (6).
Example 7
(MS) The MS system does admit a pseudopotential formulation; however it is neither local in u, v nor rational in \(\lambda \). The system


with \(\sigma =u_y\lambda +u u_t -u_t v_y +u_y v_t\), is a differential covering, meaning it is compatible modulo MS. Here the last three equations (45) determine the behaviour in the spectral parameter \(\lambda \), while the first two equations (44) yield a pseudopotential S via the system \(S_x=P\), \(S_y=Q\), \(S_t=R\). Indeed, one can verify that the differential  of the 1-form
of the 1-form  on \({\hat{M}}_u\) satisfies \(\hat{X}\mathbin {\!\lrcorner }\omega =\hat{Y}\mathbin {\!\lrcorner }\omega =0\) modulo MS and (44)–(45), where \(\hat{X}=\tilde{X}|_{\tilde{\lambda }=\lambda }\), \(\hat{Y}=\tilde{Y}|_{\tilde{\lambda }=\lambda }\) in terms of formula (8) are vector fields on \({\hat{M}}_u\) forming the Lax pair (with parameter \(\lambda \) projective).
on \({\hat{M}}_u\) satisfies \(\hat{X}\mathbin {\!\lrcorner }\omega =\hat{Y}\mathbin {\!\lrcorner }\omega =0\) modulo MS and (44)–(45), where \(\hat{X}=\tilde{X}|_{\tilde{\lambda }=\lambda }\), \(\hat{Y}=\tilde{Y}|_{\tilde{\lambda }=\lambda }\) in terms of formula (8) are vector fields on \({\hat{M}}_u\) forming the Lax pair (with parameter \(\lambda \) projective).
5.2 Twistor interpretation via contact coverings
To relate the pseudopotential formulation more closely to the dLp formulation, we focus on the first order quasilinear system for sections of \({\hat{\pi }}:{\hat{M}}_u\rightarrow M_u\) which correspond to hypersurfaces in the twistor space. We refer to this PDE system as a contact covering of \({{\mathcal {E}}}\) because the equation it defines is a codimension 2 submanifold \({{\mathcal {Q}}}\) of \(J^1{\hat{\pi }}\) (the bundle of 1-jets of sections of \({\hat{\pi }}\)), which is a contact manifold.
This viewpoint gives an alternative way to understand why contact coverings are equivalent to dLps. For this, let \(\alpha \) be a contact form on \(J^1{\hat{\pi }}\) representing the standard contact structure and let \(\alpha _{{\mathcal {Q}}}\) be its restriction on \({{\mathcal {Q}}}\). Then for  we have: \(\alpha _{{\mathcal {Q}}}\wedge \omega _{{\mathcal {Q}}}^{d-1}=0\) on shell, but \(\alpha _{{\mathcal {Q}}}\wedge \omega _{{\mathcal {Q}}}^{d-2}\not \equiv 0\), which implies that \(\alpha _{{\mathcal {Q}}}\) has a 2-dimensional radical \(\hat{\Pi }\subseteq T{{\mathcal {Q}}}\): \(\xi \mathbin {\!\lrcorner }\alpha _{{\mathcal {Q}}}=0\) and \(\xi \mathbin {\!\lrcorner }\omega _{{\mathcal {Q}}}=0\) for all \(\xi \in \hat{\Pi }\).
we have: \(\alpha _{{\mathcal {Q}}}\wedge \omega _{{\mathcal {Q}}}^{d-1}=0\) on shell, but \(\alpha _{{\mathcal {Q}}}\wedge \omega _{{\mathcal {Q}}}^{d-2}\not \equiv 0\), which implies that \(\alpha _{{\mathcal {Q}}}\) has a 2-dimensional radical \(\hat{\Pi }\subseteq T{{\mathcal {Q}}}\): \(\xi \mathbin {\!\lrcorner }\alpha _{{\mathcal {Q}}}=0\) and \(\xi \mathbin {\!\lrcorner }\omega _{{\mathcal {Q}}}=0\) for all \(\xi \in \hat{\Pi }\).
If \({{\mathcal {Q}}}\) is quasilinear, as we require in the definition of a contact covering, then \(\hat{\Pi }\) is projectible along the fibres \(\pi _{1,0}:{{\mathcal {Q}}}\rightarrow J^0\hat{\pi }={\hat{M}}_u\) and so it induces a pushforward distribution of rank 2 in \(T{\hat{M}}_u\), which is a dLp in our formalism. This is how a nonlinear covering induces a linear one, and the inverse relation is given by a lift.
We summarize the observed relations into the following diagram, intertwining the twistor and jet concepts:

Here the dotted arrow is the restriction of the jet-projection to the contact covering \({{\mathcal {Q}}}\), arrows labelled by \(\hat{\Pi }\) are (local) quotients by the corresponding foliations, and \({{\mathcal {T}}\!w}^{d-1}\) is the mini-twistor or the twistor space for \(d=3\) or \(d=4\) respectively.
The dashed arrow is well-defined locally, when a local coordinate (spectral parameter) on the fibre \({\hat{M}}_u\) is chosen, but it may fail to exist globally with respect to the spectral parameter \(\lambda \) and locally with respect to the dependent variable u. For \(d=3\), this is precisely the theory of pseudopotentials as discussed in Sect. 5.1. In this case, the space \({{\mathbb {P}}}(T^*{{\mathcal {T}}\!w})\) is the real Penrose twistor space (projecting to the Hitchin mini-twistor space with fibre \({{\mathbb {P}}}^1\)) that embeds into the complex twistor space \({{\mathcal {T}}\!w}_{{\mathbb {C}}}\), which is the complexification of \({{\mathcal {T}}\!w}\) of the case \(d=4\), via a conformal Killing reduction [20]. We leave to the reader a specification of relations between different real forms (signatures of the conformal structure—related by Wick rotations in physics language).
When \(d=4\) an analogue of the theory of pseudopotentials has been developed in [33]. Geometrically, this involves making a further projection to \({{\mathbb {P}}}(T^*M_u)\) on the left hand side of the above diagram (this is why the Lax pairs of [33] are homogeneous in \(\partial \psi \) for the covering function \(\psi \)). This is a 7-dimensional contact manifold, so two equations suffice to define a 5-dimensional submanifold \({\hat{M}}_u\). In this formalism the Lax pair is given by contact hamiltonian vector fields.
5.3 Extensions of the theory
First, as noted in the introduction, in 2D, the theory of dispersionless Lax pairs is vacuous, essentially because there is only one 2-plane congruence. However, if we relax the assumption that the Lax pair is transverse to the fibres of \({\hat{M}}_u\) over \(M_u\), this objection evaporates. The characteristic condition means that at points of tangency, the projection of the Lax distribution is a characteristic direction. In particular, when the characteristic variety is a quadric (two points), we expect two points of tangency, with the background given by the spinor-vortex equations [1, 2].
Secondly, it would be useful to be able to relax the requirement that the PDE system \(F:J^\ell (M,{{\mathcal {V}}})\rightarrow {{\mathcal {W}}}\) determined in the sense that \(\mathop {\mathrm {rank}}\nolimits ({{\mathcal {W}}})=\mathop {\mathrm {rank}}\nolimits ({{\mathcal {V}}})\). The theory in this paper should at least extend to (formally) overdetermined systems (\(\mathop {\mathrm {rank}}\nolimits ({{\mathcal {W}}})\geqslant \mathop {\mathrm {rank}}\nolimits ({{\mathcal {V}}})\)) which are compatible, so that the characteristic variety is a hypersurface. We would then need to use the compatibility conditions to generalize Theorem 1.
For truly overdetermined systems, with characteristic variety of higher codimension, it would be necessary also to replace Lax pairs by Lax distributions of higher rank. Recently the characteristic property was confirmed in [18] for paraconformal structures generalizing EW structures to higher dimension, and we suggest that it applies universally.
Finally, with the latter idea, the restriction to dimensions \(d=3,4\) can be relaxed. This would extend the framework of integrability via geometry to a wider context.
References
Burtsev, S.P., Zakharov, V.E., Mikhaĭlov, A.V.: The inverse scattering method with a variable spectral parameter. Teoret. Mat. Fiz. 70, 323–341 (1987)
Calderbank, D.M.J.: Integrable background geometries. SIGMA 10, 34 (2014)
Calogero, F., Nucci, M.C.: Lax pairs galore. J. Math. Phys. 32, 72–74 (1991)
Cartan, E.: Les systémes de Pfaff à cinq variables et les équations aux dérivées partielles du second ordre. Ann. Sci. Ecole Norm. Sup. 3(27), 109–192 (1910)
Cartan, E.: Sur une classe d’espaces de Weyl. Ann. Sci. École Norm. Sup. 3(60), 1–16 (1943)
Doubrov, B., Ferapontov, E.V.: On the integrability of symplectic Monge-Ampère equations. J. Geom. Phys. 60, 1604–1616 (2010)
Doubrov, B., Ferapontov, E.V., Kruglikov, B., Novikov, V.: On the integrability in Grassmann geometries: integrable systems associated with fourfolds Gr\((3,5)\). Proc. LMS 116, 1269–1300 (2018)
Doubrov, B., Ferapontov, E.V., Kruglikov, B., Novikov, V.: Integrable systems in 4D associated with sixfolds in Gr\((4,6)\). Int. Math. Res. Notices 21, 6585–6613 (2019)
Dubrovin, B.A., Novikov, S.P.: Hydrodynamics of weakly deformed soliton lattices: differential geometry and Hamiltonian theory. Russian Math. Surv. 44(6), 35–124 (1989)
Dunajski, M.: A class of Einstein-Weyl spaces associated to an integrable system of hydrodynamic type. J. Geom. Phys. 51(1), 126–137 (2004)
Dunajski, M.: An interpolating dispersionless integrable system. J. Phys. A 41, 315202 (2008)
Dunajski, M., Ferapontov, E., Kruglikov, B.: On the Einstein-Weyl and conformal self-duality equations. J. Math. Phys. 56, 083501 (2015)
Dunajski, M., Grant, J.D.E., Strachan, I.A.B.: Multidimensional integrable systems and deformations of Lie algebra homomorphisms. J. Math. Phys. 48, 093502 (2007)
Dunajski, M., Mason, L.J., Tod, P.: Einstein-Weyl geometry, the dKP equation and twistor theory. J. Geom. Phys. 37, 63–93 (2001)
Ferapontov, E.V., Huard, B., Zhang, A.: On the central quadric ansatz: integrable models and Painlevé reductions. J. Phys. A 45, 195–204 (2012)
Ferapontov, E.V., Khusnutdinova, K.R.: Hydrodynamic reductions of multi-dimensional dispersionless PDEs: the test for integrability. J. Math. Phys. 45(6), 2365–2377 (2004)
Ferapontov, E.V., Kruglikov, B.: Dispersionless integrable systems in 3D and Einstein-Weyl geometry. J. Differ. Geom. 97, 215–254 (2014)
Ferapontov, E.V., Kruglikov, B.: Dispersionless integrable hierarchies and GL\((2,{\mathbb{R}})\) geometry. Math. Proc. Cambridge Phil. Soc. 1–26, (2019). https://doi.org/10.1017/S0305004119000355
Hitchin, N.J.: Complex Manifolds and Einstein’s Equations, Twistor Geometry and Nonlinear Systems (Primorsko, 1980), 73–99. Lecture Notes in Math, vol. 970. Springer, Berlin-New York (1982)
Jones, P.E., Tod, K.P.: Minitwistor spaces and Einstein-Weyl spaces. Classical Quantum Gravity 2(4), 565–577 (1985)
Krasil’shchik, J., Verbovetsky, A.: Geometry of jet spaces and integrable systems. J. Geom. Phys. 61, 1633–1674 (2011)
Kruglikov, B., Lychagin, V.: Geometry of differential equations, Handbook of Global Analysis, Ed. D.Krupka, D.Saunders, Elsevier, 725-772 (2008)
Kruglikov, B., Morozov, O.: Integrable dispersionless PDE in 4D, their symmetry pseudogroups and deformations. Lett. Math. Phys. 105, 1703–1723 (2015)
Manakov, S.V., Santini, P.M.: The Cauchy problem on the plane for the dispersionless Kadomtsev-Petviashvili equation. JETP Lett. 83, 462–466 (2006)
Marvan, M.: On the spectral parameter problem. Acta Appl. Math. 109, 239–255 (2010)
Mason, L.J., Woodhouse, N.M.J.: Integrability, self-duality, and twistor theory, L.M.S. Monographs 15, Oxford University Press (1996)
Odesskii, A.V., Sokolov, V.V.: Integrable pseudopotentials related to generalized hypergeometric functions. Selecta Math. (N.S.) 16, 145–172 (2010)
Pavlov, M.V., Chang, J.H., Chen, Y.T.: Integrability of the Manakov–Santini hierarchy, arXiv:0910.2400 (2009)
Penrose, R.: Nonlinear gravitons and curved twistor theory. Gen. Relat. Gravitation 7(1), 31–52 (1976)
Plebański, J.F.: Some solutions of complex Einstein equations. J. Math. Phys. 16, 2395–2402 (1975)
Plebański, J.F., Robinson, I.: Left-degenerate vacuum metrics. Phys. Rev. Lett. 37, 493–495 (1976)
Prykarpatski, A.K.: On the linearization covering technique and its application to integrable nonlinear differential systems. SIGMA 14, 023 (2018)
Sergyeyev, A.: New integrable \((3+1)\)-dimensional systems and contact geometry. Lett. Math. Phys. 108, 359–376 (2018)
Spencer, D.C.: Over-determined systems of linear partial differential equations. Bull. Am. Math. Soc. 75, 179–239 (1969)
Tsarev, S.P.: Geometry of hamiltonian systems of hydrodynamic type. Generalized hodograph method, Izvestija AN USSR Math. 54(5), 1048–1068 (1990)
Vinogradov, A.M.: Category of nonlinear differential equations, Global Analysis Studies and Applications I, Lect. Notes Math. 1108, Springer–Verlag, 77–102 (1984)
Ward, R.S.: Einstein–Weyl spaces and \(SU(\infty )\) Toda fields, Class. Quantum Grav. 7, no. 4 (1990)
Zakharov, V.E.: Dispersionless limit of integrable systems in \(2+1\) dimensions. In: Ercolani, N.M., et al. (eds.) Singular Limits of Dispersive Waves, pp. 165–174. NY, Plenum Press (1994)
Acknowledgements
We are grateful to Jenya Ferapontov for helpful discussions. In particular, he pointed out that dispersionless Lax pairs for PDEs of Hirota type are always characteristic, suggesting that this might be true more generally, and later drew our attention to difficulties in establishing the projective property for Lax pairs in 3D. We also thank the referee for detailed comments which greatly improved the clarity of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by N. Nekrasov
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Calderbank, D.M.J., Kruglikov, B. Integrability via Geometry: Dispersionless Differential Equations in Three and Four Dimensions. Commun. Math. Phys. 382, 1811–1841 (2021). https://doi.org/10.1007/s00220-020-03913-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03913-y





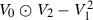 is conformal to the inverse metric. In particular,
is conformal to the inverse metric. In particular,