Abstract
In this paper we shall describe some correlation function computations in perturbative heterotic strings that, for example, in certain circumstances can lend themselves to a heterotic generalization of quantum cohomology calculations. Ordinary quantum chiral rings reflect worldsheet instanton corrections to correlation functions involving products of elements of Dolbeault cohomology groups on the target space. The heterotic generalization described here involves computing worldsheet instanton corrections to correlation functions defined by products of elements of sheaf cohomology groups. One must not only compactify moduli spaces of rational curves, but also extend a sheaf (determined by the gauge bundle) over the compactification, and linear sigma models provide natural mechanisms for doing both. Euler classes of obstruction bundles generalize to this language in an interesting way.
Similar content being viewed by others
References
Adams, A., Basu, A., Sethi, S.: (0,2) duality. Adv. Theor. Math. Phyp. 7, 865–950 (2004)
Distler, J., Greene, B., Morrison, D.: Resolving singularities in (0,2) models. Nucl. Phys. B481, 289–312 (1996)
Beasley, C., Witten, E.: Residues and worldsheet instantons. JHEP 0310, 065 (2003)
Dine, M., Seiberg, N., Wen, X.-G., Witten, E.: Nonperturbative effects on the string worldsheet. Nucl. Phys. B278, 769–789 (1986)
Witten, E., Bagger, J.: Quantization of Newton's constant in certain supergravity theories. Phys. Lett. B115, 202–206 (1982)
Distler, J.: Notes on
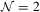 sigma models. In Trieste 1992, Proceedings, String theory and quantum gravity '92, Singapore: world scientific, 1992, pp. 234–256
sigma models. In Trieste 1992, Proceedings, String theory and quantum gravity '92, Singapore: world scientific, 1992, pp. 234–256Schwarz, A.: Sigma models having supermanifolds as target spaces. Lett. Math. Phys. 38, 91–96 (1996)
Silverstein, E., Witten, E.: Criteria for conformal invariance of (0,2) models. Nucl. Phys. B444, 161–190 (1995)
Berglund, P., Candelas, P., de la Ossa, X., Derrick, E., Distler, J., Hubsch, T.: On the instanton contributions to the masses and couplings of E 6 singlets. Nucl. Phys. B454, 127–163 (1995)
Basu, A., Sethi, S.: Worldsheet stability of (0,2) linear sigma models. Phys. Rev. D68, 025003 (2003)
Antoniadis, I., Gava, E., Narain, K., Taylor, T.: Topological amplitudes in string theory. Nucl. Phys. B413, 162–184 (1994)
Distler, J., Greene, B.: Aspects of (2,0) string compactifications. Nucl. Phys. B304, 1–62 (1988)
Okonek, C., Schneider, M., Spindler, H.: Vector Bundles on Complex Projective Spaces. Boston: Birkhäuser, 1980
Aspinwall, P., Morrison, D.: Topological field theory and rational curves. Common. Math. Phys. 151, 245–262 (1993)
Witten, E.: Topological sigma models. Common. Math. Phys. 118, 411–449 (1988)
Witten, E.: On the structure of the topological phase of two-dimensional gravity. Nucl. Phys. B340, 281–332 (1990)
Kontsevich, M.: Enumeration of rational curves via torus actions. In The Moduli Space of Curves (Texel Island, 1994), Dijkgraaf, R., Faber C., van der Geer, G. eds., Progress in Math. 129, Boston-Basel-Berlin: Birkhäuser, 1995, pp. 335–368
Klyachko, A. A.: Equivariant bundles on toral varieties. Math. USSR Izvestiya 35, 337–375 (1990)
Knutson, A., Sharpe, E.: Sheaves on toric varieties for physics. Adv. Theor. Math. Phys. 2, 865–948 (1998)
Morrison, D., Plesser, R.: Summing the instantons: quantum cohomology and mirror symmetry in toric varieties. Nucl. Phys. B440, 279–354 (1995)
Atiyah, M.: Complex analytic connections in fibre bundles. Trans. Amer. Math. Soc. 85, 181–207 (1957)
Witten, E.: Phases of
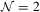 theories in two dimensions. Nucl. Phys. B403, 159–222 (1993)
theories in two dimensions. Nucl. Phys. B403, 159–222 (1993)Distler, J., Kachru, S.: (0,2) Landau-Ginzburg theory. Nucl. Phys. B413, 213–243 (1994)
Beauville, A.: Complex Algebraic Surfaces. Second edition, Cambridge: Cambridge University Press, 1996
Sharpe, E.: Kähler cone substructure. Adv. Theor. Math. Phys. 2 1441–1462 (1999)
Katz, S., Sharpe, E.: Notes on certain (0,2) correlation functions, http://arxiv.org/list/hep-th/0406226, 2004, the preprint version of this paper
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by N.A. Nekrasov
Rights and permissions
About this article
Cite this article
Katz, S., Sharpe, E. Notes on Certain (0,2) Correlation Functions. Commun. Math. Phys. 262, 611–644 (2006). https://doi.org/10.1007/s00220-005-1443-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-005-1443-1



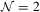 sigma models. In Trieste 1992, Proceedings, String theory and quantum gravity '92, Singapore: world scientific, 1992, pp. 234–256
sigma models. In Trieste 1992, Proceedings, String theory and quantum gravity '92, Singapore: world scientific, 1992, pp. 234–256