Abstract
Recently an infinite family of explicit Sasaki–Einstein metrics Y
p,q on S
2×S
3 has been discovered, where p and q are two coprime positive integers, with q<p. These give rise to a corresponding family of Calabi–Yau cones, which moreover are toric. Aided by several recent results in toric geometry, we show that these are Kähler quotients  namely the vacua of gauged linear sigma models with charges (p,p,−p+q,−p−q), thereby generalising the conifold, which is p=1,q=0. We present the corresponding toric diagrams and show that these may be embedded in the toric diagram for the orbifold
namely the vacua of gauged linear sigma models with charges (p,p,−p+q,−p−q), thereby generalising the conifold, which is p=1,q=0. We present the corresponding toric diagrams and show that these may be embedded in the toric diagram for the orbifold  for all q<p with fixed p. We hence find that the Y
p,q manifolds are AdS/CFT dual to an infinite class of
for all q<p with fixed p. We hence find that the Y
p,q manifolds are AdS/CFT dual to an infinite class of  superconformal field theories arising as IR fixed points of toric quiver gauge theories with gauge group SU(N)2
p. As a non–trivial example, we show that Y
2,1 is an explicit irregular Sasaki–Einstein metric on the horizon of the complex cone over the first del Pezzo surface. The dual quiver gauge theory has already been constructed for this case and hence we can predict the exact central charge of this theory at its IR fixed point using the AdS/CFT correspondence. The value we obtain is a quadratic irrational number and, remarkably, agrees with a recent purely field theoretic calculation using a-maximisation.
superconformal field theories arising as IR fixed points of toric quiver gauge theories with gauge group SU(N)2
p. As a non–trivial example, we show that Y
2,1 is an explicit irregular Sasaki–Einstein metric on the horizon of the complex cone over the first del Pezzo surface. The dual quiver gauge theory has already been constructed for this case and hence we can predict the exact central charge of this theory at its IR fixed point using the AdS/CFT correspondence. The value we obtain is a quadratic irrational number and, remarkably, agrees with a recent purely field theoretic calculation using a-maximisation.
Similar content being viewed by others
References
Maldacena, J.M.: The large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 2, 231 (1998) [Int. J. Theor. Phys. 38, 1113 (1999)]
Kehagias, A.: New type IIB vacua and their F-theory interpretation. Phys. Lett. B 435, 337 (1998)
Klebanov, I.R., Witten, E.: Superconformal field theory on threebranes at a Calabi-Yau singularity. Nucl. Phys. B 536, 199 (1998)
Acharya, B.S., Figueroa-O'Farrill, J.M., Hull, C.M., Spence, B.: Branes at conical singularities and holography. Adv. Theor. Math. Phys. 2, 1249 (1999)
Morrison, D.R., Plesser, M.R.: Non-spherical horizons. I. Adv. Theor. Math. Phys. 3, 1 (1999)
Gauntlett, J.P., Martelli, D., Sparks, J., Waldram, D.: Sasaki-Einstein metrics on S 2 × S 3. Adv. Theor. Math. Phys. 8, 711 (2004)
Gauntlett, J.P., Martelli, D., Sparks, J., Waldram, D.: Supersymmetric AdS5 solutions of M-theory. Class. Quant. Grav. 21, 4335 (2004)
Cheeger, J., Tian, G.: On the cone structure at infinity of Ricci flat manifolds with Euclidean volume growth and quadratic curvature decay. Invent. Math. 118(3), 493–571 (1994)
Intriligator, K., Wecht, B.: The exact superconformal R-symmetry maximizes a. Nucl. Phys. B 667, 183 (2003)
Gubser, S.S.: Einstein manifolds and conformal field theories. Phys. Rev. D 59 (1999) 025006
Feng, B., Hanany, A., He, Y.H.: D-brane gauge theories from toric singularities and toric duality. Nucl. Phys. B 595, 165 (2001)
Herzog, C.P., Walcher, J.: Dibaryons from exceptional collections. JHEP 0309, 060 (2003)
Herzog, C.P.: Exceptional collections and del Pezzo gauge theories. JHEP 0404, 069 (2004)
Bertolini, M., Bigazzi, F., Cotrone, A.: New checks and subtleties for AdS/CFT and a-maximization. JHEP 0412, 024 (2004)
Gauntlett, J.P., Martelli, D., Sparks, J., Waldram, D.: A new infinite class of Sasaki-Einstein manifolds. http://arXiv:org/list/hep-th/0403038, 2004
Gauntlett, J.P., Martelli, D., Sparks, J. Waldram, D.: Supersymmetric AdS Backgrounds in String and M-theory. http://arXiv:org/list/hep-th/0411194, 2004
Chen, W., Lu, H., Pope, C.N., Vazquez-Poritz, J.F.: A Note on Einstein–Sasaki Metrics in D ≥7. http://arXiv.org/list/hep-th/0411218, 2004
Tian, G.: On Kähler–Einstein metrics on certain Kähler manifolds with c 1(M)>0. Invent. Math. 89, 225–246 (1987)
Tian, G., Yau, S.T.: On Kähler–Einstein metrics on complex surfaces with C 1>0. Commun. Math. Phys. 112, 175–203 (1987)
Lerman, E.: Contact toric manifolds. J. Symplectic Geom. 1(4), 785–828 (2003)
Delzant, T.: Hamiltoniens periodiques et images convexes de l'application moment. Bull. Soc. Math. France 116(3), 315–339 (1988)
Witten, E.: Phases of
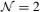 theories in two dimensions. Nucl. Phys. B 403, 159 (1993)
theories in two dimensions. Nucl. Phys. B 403, 159 (1993)Beasley, C., Greene, B.R., Lazaroiu, C.I., Plesser, M.R.: D3-branes on partial resolutions of abelian quotient singularities of Calabi-Yau threefolds. Nucl. Phys. B 566, 599 (2000)
Witten, E.: Baryons and branes in anti de Sitter space. JHEP 9807, 006 (1998)
Berenstein, D., Herzog, C.P., Klebanov, I.R.: Baryon Spectra and AdS/CFT Correspondence. JHEP 0206, 047 (2002)
Smale, S.: On the structure of 5-manifolds. Ann. Math. 75, 38–46 (1962)
Friedrich, Th., Kath, I.: Einstein manifolds of dimension five with small first eigenvalue of the Dirac operator. J. Differ. Geom. 29, 263–279 (1989)
Matsushima, Y.: Sur la structure du groupe d'homéomorphismes analytiques d'une certaine variété kaehlérienne. Nagoya Math. J. 11, 145–150 (1957)
Boyer, C.P., Galicki, K.: New Einstein metrics in dimension five. J. Differ. Geom. 57(3), 443–463 (2001)
Boyer, C.P., Galicki, K., Nakamaye, M.: On the Geometry of Sasakian–Einstein 5-Manifolds. Math. Ann. 325(3), 485–524 (2003)
Boyer, C.P., Galicki, K., Nakamaye, M.: Sasakian–Einstein structures on 9#(S 2× S 3). Trans. Amer. Math. Soc. 354(8), 2983–2996 (2002)
Boyer, C.P., Galicki, K.: New Einstein metrics on 8#(S 2× S 3). Differential Geom. Appl. 19(2), 245–251 (2003)
Wang, M.Y., Ziller, W.: Einstein metrics on principal torus bundles. J. Diff. Geom. 31, 215 (1990)
Boyer, C.P., Galicki, K.: 3-Sasakian Manifolds. Surveys Diff. Geom. 7, 123–184 (1999)
Falcao de Moraes, S., Tomei, C.: Moment maps on symplectic cones. Pacif. J. Math. 181(2), 357–375 (1997)
Atiyah, M.F.: Convexity and commuting Hamiltonians. Bull. London Math. Soc. 14, 1–15 (1982)
Guillemin, V., Sternberg, S.: Convexity properties of the moment mapping. Invent. Math. 67, 491–513 (1982)
Lerman, E., Tolman, S.: Hamiltonian torus actions on symplectic orbifolds and toric varieties. http://arXiv.org/list/dg-ga/9511008, 1995
Boyer, C.P., Galicki, K.: A Note on Toric Contact Geometry. J. Geom. and Phys. 35, 288–298 (2000)
Lerman, E.: Homotopy Groups of K-Contact Toric Manifolds. Trans. Amer. Math. Soc. 356(10), 4075–4083 (2004)
Page, D.N.: A compact rotating gravitational instanton. Phys. Lett. 79B(3), 235–238 (1978)
Feng, B., Franco, S., Hanany, A., He, Y.H.: Symmetries of toric duality. JHEP 0212, 076 (2002)
Dall'Agata, G.: N = 2 conformal field theories from M2-branes at conifold singularities. Phys. Lett. B 460, 79 (1999)
Fabbri, D., Fre', P., Gualtieri, L., Reina, C., Tomasiello, A., Zaffaroni, A., Zampa, A.: 3D superconformal theories from Sasakian seven-manifolds: New nontrivial evidences for AdS(4)/CFT(3). Nucl. Phys. B 577, 547 (2000)
Ceresole, A., Dall'Agata, G., D'Auria, R., Ferrara, S.: M-theory on the Stiefel manifold and 3d conformal field theories. JHEP 0003, 011 (2000)
Intriligator, K., Wecht, B.: Baryon charges in 4D superconformal field theories and their AdS duals. Commun. Math. Phys. 245, 407 (2004)
Candelas, P., de la Ossa, X.C.: Comments On Conifolds. Nucl. Phys. B 342, 246 (1990)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by G.W. Gibbons
Rights and permissions
About this article
Cite this article
Martelli, D., Sparks, J. Toric Geometry, Sasaki–Einstein Manifolds and a New Infinite Class of AdS/CFT Duals. Commun. Math. Phys. 262, 51–89 (2006). https://doi.org/10.1007/s00220-005-1425-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-005-1425-3




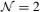 theories in two dimensions. Nucl. Phys. B 403, 159 (1993)
theories in two dimensions. Nucl. Phys. B 403, 159 (1993)