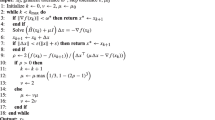Skip to main content
SpringerLink
Log in

Efficient low-rank solution of generalized Lyapunov equations

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

An iterative method for the low-rank approximate solution of a class of generalized Lyapunov equations is studied. At each iteration, a standard Lyapunov equation is solved using Galerkin projection with an extended Krylov subspace method. This Lyapunov equation is solved inexactly, thus producing a nonstationary iteration. Several theoretical and computational issues are discussed so as to make the iteration efficient. Numerical experiments indicate that this method is competitive vis-à-vis the current state-of-the-art methods, both in terms of computational times and storage needs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The value 0.3 is an estimate of the norm \(\Vert {\mathcal M}^{-1}{\mathcal N}\Vert _F\) for the first example heat1 in Sect. 5. In general, this norm is not near one for the problems considered here, where the rank of \(N_j \ll n\), and these matrices are extremely sparse.

  2. We mention that similar slow results are obtained if one uses the tangential interpolation version of a rational Krylov method, as proposed in [7].

References

  1. Benner, P., Breiten, T.: Low-rank methods for a class of generalized Lyapunov equations and related issues. Numerische Mathematik 124, 441–470 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  2. Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences. (3rd edn.) Academic Press, New York (1979). Reprinted by SIAM, Philadelphia (1994)

  3. Damm, T.: Direct methods and ADI-preconditioned Krylov subspace methods for generalized Lyapunov equations. Numer. Linear Algebra Appl. 15, 853–871 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  4. Damm, T., Hinrichsen, D.: Newton’s method for a rational matrix equation occurring in stochastic control. Linear Algebra Appl. 332–334, 81–109 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  5. Dembo, R.S., Eisenstat, S.C., Steihaug, T.: Inexact Newton methods. SIAM J. Numer. Anal. 19, 400–408 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  6. Druskin, V., Knizhnerman, L., Simoncini, V.: Analysis of the rational Krylov subspace and ADI methods for solving the Lyapunov equation. SIAM J. Numer. Anal. 49, 1875–1898 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Druskin, V., Simoncini, V., Zaslavsky, M.: Adaptive tangential interpolation in rational Krylov subspaces for MIMO model reduction data. SIAM J. Matrix Anal. Appl. 35, 476–498 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Fasi, M.: Weighted geometric mean of large-scale matrices: numerical analysis and algorithms. Master’s thesis. Department of Computer Science. Università di Bologna, Italy, March 2015

  9. Frommer, A., Szyld, D.B.: On necessary conditions for convergence of stationary iterative methods for hermitian definite and semidefinite linear systems. Linear Algebra Appl. 453, 192–201 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Golub, G.H., Overton, M.L.: The convergence of inexact Chebyshev and Richardson iterative methods for solving linear systems. Numerische Mathematik 53, 571–593 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hu, D.Y., Reichel, L.: Krylov subspace methods for the Sylvester equation. Linear Algebra Appl. 172, 283–313 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  12. Knizhnerman, L., Simoncini, V.: Convergence analysis of the extended Krylov subspace method for the Lyapunov equation. Numerische Mathematik 118, 567–586 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kressner, D., Tobler, C.: Low-rank tensor Krylov subspace methods for parametrized linear systems. SIAM J. Matrix Anal. Appl. 32, 1288–1316 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lancaster, P., Tismenetsky, M.: The Theory of Matrices, 2nd edn. Academic Press, Orlando (1985)

    MATH  Google Scholar 

  15. Lanzkron, P.J., Rose, D.J., Szyld, D.B.: Convergence of nested classical iterative methods for linear systems. Numerische Mathematik 58, 685–702 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  16. Matthies, H.G., Zander, E.: Solving stochastic systems with low-rank tensor compression. Linear Algebra Appl. 436, 3819–3838 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Nichols, N.K.: On the convergence of two-stage iterative processes for solving linear equations. SIAM J. Numer. Anal. 10, 460–469 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  18. Penzl, T.: A cyclic low-rank Smith method for large sparse Lyapunov equations. SIAM J. Sci. Comput. 21, 1401–1418 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  19. Shank, S.D.: Low-rank Solution Methods for Large-scale Linear Matrix Equations. PhD thesis, Department of Mathematics, Temple University, May 2014

  20. Simoncini, V.. Computational methods for linear matrix equations. Preprint, Università di Bologna, March 2013, Revised January 2014. To appear in SIAM Review

  21. Simoncini, V.: A new iterative method for solving large-scale Lyapunov matrix equations. SIAM J. Sci. Comput. 29, 1268–1288 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  22. Varga, R.S.: Matrix Iterative Analysis. Prentice-Hall, Englewood Cliffs (1962). Second Edition, revised and expanded. Springer, Berlin (2000)

Download references

Acknowledgments

We are grateful to Peter Benner and Tobias Breiten for providing us with all their MATLAB codes from [1]. We also thank the referees for their questions and comments which helped improve our presentation.

Author information

Author notes

  1. Stephen D. Shank

    Present address: Center for Computational Genetics and Genomics, Temple University, Bio-Life Building (015-00) 1900 N. 12th Street, Philadelphia, PA, 19122-6078, USA

Authors and Affiliations

  1. Department of Mathematics, Temple University (038-16), 1805 N. Broad Street, Philadelphia, PA, 19122-6094, USA

    Stephen D. Shank & Daniel B. Szyld

  2. Dipartimento di Matematica, Università di Bologna, Piazza di Porta San Donato, 5, 40127, Bologna, Italy

    Valeria Simoncini

  3. IMATI-CNR, Pavia, Italy

    Valeria Simoncini

Authors
  1. Stephen D. Shank
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Valeria Simoncini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Daniel B. Szyld
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daniel B. Szyld.

Additional information

This version dated 7 October 2015. This research is supported in part by the U.S. National Science Foundation under Grants DMS-1115520 and DMS-1418882, and by the FARB12SIMO Grant of the Università di Bologna.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shank, S.D., Simoncini, V. & Szyld, D.B. Efficient low-rank solution of generalized Lyapunov equations. Numer. Math. 134, 327–342 (2016). https://doi.org/10.1007/s00211-015-0777-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-015-0777-7

Mathematics Subject Classification

Search

Navigation