Mortar multiscale finite element methods for Stokes–Darcy flows

Abstract

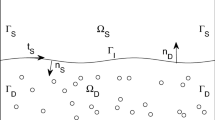
We investigate mortar multiscale numerical methods for coupled Stokes and Darcy flows with the Beavers–Joseph–Saffman interface condition. The domain is decomposed into a series of subdomains (coarse grid) of either Stokes or Darcy type. The subdomains are discretized by appropriate Stokes or Darcy finite elements. The solution is resolved locally (in each coarse element) on a fine scale, allowing for non-matching grids across subdomain interfaces. Coarse scale mortar finite elements are introduced on the interfaces to approximate the normal stress and impose weakly continuity of the normal velocity. Stability and a priori error estimates in terms of the fine subdomain scale $h$ and the coarse mortar scale $H$ are established for fairly general grid configurations, assuming that the mortar space satisfies a certain inf-sup condition. Several examples of such spaces in two and three dimensions are given. Numerical experiments are presented in confirmation of the theory.

Appendix

This Appendix is devoted to specific examples of construction of ${\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}})$ in ${\Omega }_s$.

1.1 The 2-D case

Recall that the construction of the correction ${\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}})$ in ${\Omega }_s$ in 2-D required an operator $\pi _s^h$ satisfying (4.23). In particular, given $\hat{\varvec{\ell }}$ in $H^{\frac{1}{2}}_{00}(\hat{\Gamma })^2$, one needs to construct $\hat{\pi }_j(\hat{\varvec{\ell }})$ in $\hat{X}_j$, unique solution of (4.24):

$$\begin{aligned} \forall \hat{\varvec{\mu }}\in \hat{\Lambda },\quad \int _{\hat{\Gamma }}\hat{\pi }_j(\hat{\varvec{\ell }})\cdot \hat{\varvec{\mu }}= \int _{\hat{\Gamma }} \hat{\varvec{\ell }}\cdot \hat{\varvec{\mu }}, \end{aligned}$$

and satisfying (4.25).

Here we present two simple examples of how to construct such an operator when $\Gamma _{ij}$ is a straight line segment and the traces of the discrete spaces on $\Gamma _{ij}$ are piecewise ${\mathbb {P}}_1$ finite elements, Without loss of generality, we can suppose that $\hat{\Gamma }$ is the segment $[0,1]$, that the nodes of $\hat{\mathcal T}_j$ are $0 = \hat{x}_0 < \hat{x}_1 < \dots <\hat{x}_N < \hat{x}_{N+1} =1$, and we set $\hat{h}_n = \hat{x}_{n+1}-\hat{x}_n$, $0\le n\le N$. We choose each component of the functions of $\hat{X}_j$ piecewise ${\mathbb {P}}_1$ in the subintervals $[\hat{x}_n,\hat{x}_{n+1}]$, with degrees of freedom at the nodes $\hat{x}_n$, $1 \le n \le N$.

1.1.1 First example

As a first example, we choose each component of the mortar functions of $\hat{\Lambda }$ also piecewise ${\mathbb {P}}_1$ in the subintervals $[\hat{x}_n,\hat{x}_{n+1}]$, with degrees of freedom at the nodes $\hat{x}_n$, $n=0$, $2 \le n \le N-1$, and $n=N+1$. The nodes $\hat{x}_1$ and $\hat{x}_N$ are deleted so that $\hat{X}_j$ and $\hat{\Lambda }$ have the same dimension $2N$; thus the matrix of the linear system (4.24) is square. In order to express these functions in terms of a basis, it is convenient to modify slightly the standard Lagrange basis functions for the velocity. More precisely, we define

$$\begin{aligned}&\displaystyle \hat{\varphi }_0(\hat{x})|_{[\hat{x}_0,\hat{x}_2]} = \frac{1}{\hat{h}_0+\hat{h}_1 }(\hat{x}_2 -\hat{x}),\quad \hat{\varphi }_{N+1}(\hat{x})|_{[\hat{x}_{N-1},\hat{x}_{N+1}]} = \frac{1}{\hat{h}_{N}+ \hat{h}_{N-1}}(\hat{x} -\hat{x}_{N-1}),\nonumber \\&\displaystyle \hat{\varphi }_2(\hat{x})|_{[\hat{x}_0,\hat{x}_2]} = \frac{1}{\hat{h}_0+\hat{h}_1 }(\hat{x}-\hat{x}_0),\quad \hat{\varphi }_2(\hat{x})|_{[\hat{x}_{2},\hat{x}_3]} = \frac{1}{\hat{h}_{2}}(\hat{x}_{3}-\hat{x}),\nonumber \\&\displaystyle \hat{\varphi }_{N-1}(\hat{x})|_{[\hat{x}_{N-2},\hat{x}_{N-1}]} \!=\! \frac{1}{\hat{h}_{N-1}}(\hat{x}\!-\!\hat{x}_{N-2}),\\&\displaystyle \hat{\varphi }_{N-1}(\hat{x})|_{[\hat{x}_{N-1},\hat{x}_{N+1}]} \!=\! \frac{1}{\hat{h}_{N-1} + \hat{h}_N}(\hat{x}_{N+1} - \hat{x}),\nonumber \\&\displaystyle \hat{\varphi }_n(\hat{x})|_{[\hat{x}_{n-1},\hat{x}_n]} = \frac{1}{\hat{h}_{n-1}}(\hat{x} -\hat{x}_{n-1}),\ \hat{\varphi }_n(\hat{x})|_{[\hat{x}_n,\hat{x}_{n+1}]} = \frac{1}{\hat{h}_n}(\hat{x}_{n+1} -\hat{x}), \nonumber \\&\displaystyle n=1,3\le n\le N-2, n=N,\nonumber \end{aligned}$$

(7.1)

extended by zero elsewhere. We take

$$\begin{aligned}&\displaystyle \hat{X}_j \!=\! \left\{ \hat{\varvec{v}}\!\in \! H^1_0(0,1)^2;\,\hat{\varvec{v}}(\hat{x}) \!=\! \sum _{n=1}^N \hat{\varvec{v}}_n\hat{\varphi }_n(\hat{x})\right\} , \end{aligned}$$

(7.2)

$$\begin{aligned}&\displaystyle \hat{\Lambda }\!=\! \left\{ \hat{\varvec{\mu }}\!\in \! H^1(0,1)^2;\, \hat{\varvec{\mu }}(\hat{x})\!=\! \hat{\varvec{\mu }}(\hat{x}_0)\hat{\varphi }_0(\hat{x})\!+\! \sum _{n=2}^{N-1} \hat{\varvec{\mu }}(\hat{x}_n)\hat{\varphi }_n(\hat{x}) \!+\! \hat{\varvec{\mu }}(\hat{x}_{N+1})\hat{\varphi }_{N+1}(\hat{x})\right\} .\nonumber \\ \end{aligned}$$

(7.3)

On one hand, the set $\{\hat{\varphi }_0, \hat{\varphi }_n, 2 \le n \le N-1, \hat{\varphi }_{N+1}\}$ is indeed a Lagrange basis for $\hat{\Lambda }$. On the other hand, the set $\{\hat{\varphi }_n, 1 \le n \le N\}$ is a basis but not a Lagrange basis for $\hat{X}_j$; however, it is easy to check that

$$\begin{aligned}&\hat{\varvec{v}}_1 = \hat{\varvec{v}}(\hat{x}_1) - \hat{\varvec{v}}(\hat{x}_2)\hat{\varphi }_2(\hat{x}_1),\quad \hat{\varvec{v}}_n = \hat{\varvec{v}}(\hat{x}_n),\quad 2 \le n\le N-1,\nonumber \\&\quad \hat{\varvec{v}}_N = \hat{\varvec{v}}(\hat{x}_N) - \hat{\varvec{v}}(\hat{x}_{N-1})\hat{\varphi }_{N-1}(\hat{x}_N). \end{aligned}$$

(7.4)

The system (4.24) can be decoupled into two independent systems in ${\mathbb {R}}^N$, one for each component, and each system has the form ${\varvec{M}}{\varvec{\alpha }}= {\varvec{b}}$, where ${\varvec{\alpha }}\in {\mathbb {R}}^N$ is the unknown, the non zero coefficients of ${\varvec{M}}$ per row are

$$\begin{aligned}&\displaystyle M_{1,1} = \frac{1}{6}(\hat{h}_0 + 2\hat{h}_1),\quad M_{1,2} = \frac{1}{6}(\hat{h}_0 + \hat{h}_1),\\&\displaystyle M_{2,1} =\frac{1}{6}(2\hat{h}_0 + \hat{h}_1),\quad M_{2,2} = \frac{1}{3}(\hat{h}_0 + \hat{h}_1 + \hat{h}_2),\quad M_{2,3} =\frac{\hat{h}_2}{6}, \\&\displaystyle M_{n,n-1} =\frac{\hat{h}_{n-1}}{6},\quad M_{n,n} =\frac{1}{3}(\hat{h}_{n-1}+ \hat{h}_n),\quad M_{n,n+1} = \frac{\hat{h}_{n}}{6}, 3 \le n \le N-2,\\&\displaystyle M_{N-1,N-2} = \frac{\hat{h}_{N-2}}{6},\quad M_{N-1,N-1} = \frac{1}{3} (\hat{h}_{N-2} + \hat{h}_{N-1} + \hat{h}_N),\\&\displaystyle M_{N-1,N}= \frac{1}{6}(\hat{h}_{N-1} + 2 \hat{h}_N),\quad M_{N-1,N} = \frac{1}{6}(2\hat{h}_{N-1} + \hat{h}_N),\\&\displaystyle M_{N,N} = \frac{1}{6}(\hat{h}_{N-1} + \hat{h}_N). \end{aligned}$$

Denoting by $\hat{\ell }$ a generic component of $\hat{\varvec{\ell }}$, the components of ${\varvec{b}}\in {\mathbb {R}}^N$ are

$$\begin{aligned} \begin{aligned}&b_1 = \int _{\hat{x}_0}^{\hat{x}_2} \hat{\ell }\hat{\varphi }_0,\quad b_2 =\int _{\hat{x}_0}^{\hat{x}_3} \hat{\ell }\hat{\varphi }_2, \quad b_n =\int _{\hat{x}_{n-1}}^{\hat{x}_{n+1}} \hat{\ell }\hat{\varphi }_n,\quad 3 \le n \le N-2,\\&b_{N-1} =\int _{\hat{x}_{N-2}}^{\hat{x}_{N+1}} \hat{\ell }\hat{\varphi }_{N-1},\quad b_{N} =\int _{\hat{x}_{N-1}}^{\hat{x}_{N+1}} \hat{\ell }\hat{\varphi }_{N+1}. \end{aligned} \end{aligned}$$

(7.5)

The matrix ${\varvec{M}}$ is tridiagonal but not symmetric, the coefficients of its three diagonals are all strictly positive, and it is strictly diagonally dominant, hence invertible, but this is not sufficient to obtain a sharp estimate for its inverse. To this end, we use the approach of Crouzeix and Thomée [23]. More precisely, let ${\varvec{D}}$ be the principal diagonal of ${\varvec{M}}$ and factor ${\varvec{M}}$ into ${\varvec{M}}={\varvec{D}}({\varvec{I}}+ {\varvec{K}})$ where ${\varvec{K}}$ is a tridiagonal matrix with principal diagonal zero. Denote the diagonal terms of ${\varvec{D}}$ by $d_n >0$ and note that ${\varvec{D}}^{\frac{1}{2}}$ is well-defined. The next lemma relates $\hat{\pi }_j(\hat{\ell })$ and ${\varvec{\alpha }}$. Recall that $| \cdot |$ denotes the Euclidean vector norm.

Lemma 7.1

For each component $\hat{\ell }$ of $\hat{\varvec{\ell }}$ we have

$$\begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert _{L^2(\hat{\Gamma })} \le 2 |{\varvec{D}}^{\frac{1}{2}}{\varvec{\alpha }}|. \end{aligned}$$

(7.6)

Proof

Considering the support of the basis functions $\hat{\varphi }_n$, we have

$$\begin{aligned} \begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert ^2_{L^2(\hat{\Gamma })} =&\int _{\hat{x}_0}^{\hat{x}_2} (\alpha _1 \hat{\varphi }_1 + \alpha _2 \hat{\varphi }_2)^2 + \sum _{n=2}^{N-2} \int _{\hat{x}_n}^{\hat{x}_{n+1}} (\alpha _n \hat{\varphi }_n + \alpha _{n+1} \hat{\varphi }_{n+1})^2\\&+ \int _{\hat{x}_{N-1}}^{\hat{x}_{N+1}} (\alpha _{N-1} \hat{\varphi }_{N-1} + \alpha _{N+1} \hat{\varphi }_{N+1})^2. \end{aligned} \end{aligned}$$

By substituting the expression of these integrals and rearranging terms, we derive

$$\begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert ^2_{L^2(\hat{\Gamma })}&\le \frac{2}{3}\Big (\alpha _1^2(\hat{h}_0 + \hat{h}_1) + \alpha _2^2(\hat{h}_0 + \hat{h}_1 + \hat{h}_2) + \sum \limits _{n=3}^{N-2} \alpha _n^2(\hat{h}_{n-1} + \hat{h}_n)\\&\qquad + \alpha _{N-1}^2(\hat{h}_{N-2} + \hat{h}_{N-1} + \hat{h}_N ) + \alpha _{N}^2(\hat{h}_{N-1} + \hat{h}_N )\Big ). \end{aligned}$$

In view of the diagonal terms $d_n$ of ${\varvec{D}}$, this can be written

$$\begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert ^2_{L^2(\hat{\Gamma })} \le 2\left( \alpha _1^2 \frac{\hat{h}_0 + \hat{h}_1}{3} + \sum _{n=2}^{N-1} \alpha _n^2 d_n + \alpha _{N}^2\frac{ \hat{h}_{N-1} + \hat{h}_N}{3}\right) . \end{aligned}$$

But

$$\begin{aligned} \frac{\hat{h}_0 + \hat{h}_1}{3} =2 d_1 \frac{\hat{h}_0 + \hat{h}_1}{\hat{h}_0 + 2\hat{h}_1} <2 d_1,\ \hbox {and similarly}\ \frac{\hat{h}_{N-1} + \hat{h}_N}{3} <2 d_N. \end{aligned}$$

Hence

$$\begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert _{L^2(\hat{\Gamma })} \le 2 \left( \sum _{n=1}^{N} \alpha _n^2 d_n\right) ^{\frac{1}{2}}, \end{aligned}$$

(7.7)

whence (7.6).

This lemma shows that an $L^2$ bound for $\hat{\pi }_j(\hat{\ell })$ relies on a bound for $|{\varvec{D}}^{\frac{1}{2}}{\varvec{\alpha }}|$. But ${\varvec{D}}^{\frac{1}{2}}{\varvec{\alpha }}$ has also the following expression

$$\begin{aligned} {\varvec{D}}^{\frac{1}{2}}{\varvec{\alpha }}= \big ({\varvec{I}}+ {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{-\frac{1}{2}}\big )^{-1}\big ({\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}\big ). \end{aligned}$$

Therefore Lemma 7.1 implies that

$$\begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })\Vert _{L^2(\hat{\Gamma })} \le 2 \Vert \big ({\varvec{I}}+ {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{-\frac{1}{2}}\big )^{-1}\Vert _2 |{\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}|, \end{aligned}$$

(7.8)

where $\Vert \cdot \Vert _2$ denotes the matrix norm subordinated by the Euclidean norm, and more generally $\Vert \cdot \Vert _p$ is the matrix norm subordinated by the $l^p$ vector norm. The next lemma gives a bound for $|{\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}|$.

Lemma 7.2

We have

$$\begin{aligned} |{\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}| \le \sqrt{3}\Vert \hat{\ell }\Vert _{L^2(\hat{\Gamma })}. \end{aligned}$$

(7.9)

Proof

By integrating the basis functions $\hat{\varphi }_n$, we derive

$$\begin{aligned} |{\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}|^2&= \sum _{n=1}^N d_n^{-1} b_n^2\nonumber \\&\le \frac{1}{3}\left( \frac{\hat{h}_0 + \hat{h}_1}{d_1}\Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_0,\hat{x}_2)} + \frac{\hat{h}_0 + \hat{h}_1 + \hat{h}_2}{d_2}\Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_0,\hat{x}_3)} \right. \nonumber \\&\qquad \left. + \sum _{n=3}^{N-2} \frac{\hat{h}_{n-1} \!+\! \hat{h}_n}{d_n}\Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_{n-1},\hat{x}_{n+1})}\!+\! \frac{\hat{h}_{N-2} \!+\! \hat{h}_{N-1} \!+\!\hat{h}_{N}}{d_{N-1}}\Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_{N-2},\hat{x}_{N+1})} \right. \nonumber \\&\qquad \left. \!+\! \frac{\hat{h}_{N-1} \!+\!\hat{h}_{N}}{d_{N}}\Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_{N-1},\hat{x}_{N+1})}\right) . \end{aligned}$$

(7.10)

Then proceeding as in Lemma 7.1, we obtain

$$\begin{aligned} |{\varvec{D}}^{-\frac{1}{2}}{\varvec{b}}|^2&\le \Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_0,\hat{x}_1)} + \Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_0,\hat{x}_2)} + \sum _{n=1}^N \Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_{n-1},\hat{x}_{n+1})} + \Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_N,\hat{x}_{N+1})} \\&+ \Vert \hat{\ell }\Vert ^2_{L^2(\hat{x}_{N-1},\hat{x}_{N+1})}, \end{aligned}$$

whence (7.9).

It remains to evaluate $\Vert \big ({\varvec{I}}+ {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{-\frac{1}{2}}\big )^{-1}\Vert _2$. Following Crouzeix and Thomée, we introduce the following constraint on the mesh length $\hat{h}_n$:

Hypothesis 7.1

There exist two constants $c_0 >0$ and $\gamma >0$ independent of $N$ such that

$$\begin{aligned} \forall n,m, 0\le n,m \le N,\quad \frac{\hat{h}_n}{\hat{h}_m} \le c_0 \gamma ^{|n-m|}. \end{aligned}$$

(7.11)

This condition holds for quasi-uniform meshes, but it is also satisfied by much more general meshes.

Proposition 7.1

If Hypothesis 7.1 holds with suitable constants $c_0$ and $\gamma$, then there exists a constant $C$ independent of $N$ and $j$ such that

$$\begin{aligned} \Vert \big ({\varvec{I}}+ {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{-\frac{1}{2}}\big )^{-1}\Vert _2 \le C. \end{aligned}$$

(7.12)

Hence with the same constant $C$,

$$\begin{aligned} \forall \hat{\varvec{\ell }}\in L^2(\hat{\Gamma })^2,\quad \Vert \hat{\pi }_j(\hat{\varvec{\ell }})\Vert _{L^2(\hat{\Gamma })} \le 2 \sqrt{3} C\Vert \hat{\varvec{\ell }}\Vert _{L^2(\hat{\Gamma })}. \end{aligned}$$

(7.13)

Proof

The proof follows the ideas of [23] but is more complex because the functions of $\hat{X}_j$ vanish at the end points of $\hat{\Gamma }$ whereas those of $\hat{\Lambda }$ do not. Let us prove convergence of the series

$$\begin{aligned} \sum _{r=1}^\infty \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _2; \end{aligned}$$

this will yield

$$\begin{aligned} \Vert \big ({\varvec{I}}+ {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{-\frac{1}{2}}\big )^{-1}\Vert _2 \le 1 + \sum _{r=1}^\infty \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _2. \end{aligned}$$

(7.14)

As ${\varvec{K}}$ has three diagonals, then ${\varvec{K}}^r$ has $2r+1$ diagonals. In addition, since the coefficients of these diagonals are non negative, this implies that

$$\begin{aligned} \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _1 \le (2r+1) \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _\infty , \end{aligned}$$

and by interpolation,

$$\begin{aligned} \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _2 \le (2r+1)^{\frac{1}{2}} \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _\infty . \end{aligned}$$

Therefore

$$\begin{aligned} \Vert {\varvec{D}}^{\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{-\frac{1}{2}}\Vert _2 \le \sup _{|n-m| \le 2 r}\Big (\frac{d_n}{d_m}\Big )^{\frac{1}{2}} (2r+1)^{\frac{1}{2}}\Vert {\varvec{K}}\Vert ^r_\infty . \end{aligned}$$

(7.15)

Thus a sufficient condition for the series convergence is:

$$\begin{aligned} \sup _{|n-m| \le 2 r}\Big (\frac{d_n}{d_m}\Big )^{\frac{1}{2}} \le c\Big (\frac{\delta }{\Vert {\varvec{K}}\Vert _\infty }\Big )^r, \end{aligned}$$

(7.16)

where $c>0$ and $0<\delta <1$ are two constants independent of $r$. First, assuming Hypothesis 7.1, a simple but tedious computation gives for $0 <\gamma <2$

$$\begin{aligned} \sup _{|n-m| \le 2 r}\frac{d_n}{d_m}\le 2c_0(1 + \gamma + \gamma ^2) \gamma ^{2r}. \end{aligned}$$

(7.17)

Hence the series converges if

$$\begin{aligned} \gamma < \mathrm{Min}\left( 2,\frac{1}{\Vert {\varvec{K}}\Vert _\infty }\right) . \end{aligned}$$

It is easy to check that

$$\begin{aligned} \Vert {\varvec{K}}\Vert _\infty&= \mathrm{Max}\left( \frac{\hat{h}_0 + \hat{h}_1}{\hat{h}_0 + 2\hat{h}_1}, \frac{\hat{h}_N+\hat{h}_{N-1} }{\hat{h}_N + 2\hat{h}_{N-1}}, \frac{1}{2}\left( 1+ \frac{\hat{h}_0}{ \hat{h}_0 + \hat{h}_1 + \hat{h}_2}\right) , \right. \\&\qquad \quad \left. \frac{1}{2}\left( 1+ \frac{\hat{h}_N}{\hat{h}_{N-2} + \hat{h}_{N-1} + \hat{h}_{N}}\right) \right) . \end{aligned}$$

To simplify the notation, set $\theta = c_0\gamma$. Owing to Hypothesis 7.1, for $\theta \ge 1$, we have

$$\begin{aligned} \Vert {\varvec{K}}\Vert _\infty \le \frac{1}{2}\left( 1+ \mathrm{Max}\big (\frac{\theta }{2+ \theta }, \frac{\theta ^2}{1+ \theta + \theta ^2}\big )\right) = \frac{1}{2}\left( 1 + \frac{\theta ^2}{1+ \theta + \theta ^2}\right) .\qquad \quad \end{aligned}$$

(7.18)

Take for instance $\theta = \frac{3}{2}$; then (7.18) yields $\Vert {\varvec{K}}\Vert _\infty < \frac{3}{4}$. Therefore the series converges for $\gamma = \frac{4}{3}$ and in turn $c_0 = \frac{9}{8}$. Then (7.13) is an immediate consequence of Lemmas 7.1 and 7.2.

Now we estimate $\hat{\pi }_j(\hat{\varvec{\ell }})$ in $H^1(\hat{\Gamma })^2$ for $\hat{\varvec{\ell }}\in H^1_0(\hat{\Gamma })^2$. First, we have the analogue of Lemma 7.1.

Lemma 7.3

We keep the notation of Lemma 7.1. Under Hypothesis 7.1 with $\gamma >1$, we have

$$\begin{aligned} |\hat{\pi }_j(\hat{\ell })|_{H^1(\hat{\Gamma })} \le \sqrt{\frac{2}{3}}\left( c_0\gamma (1+\gamma ) + 2 + \frac{c_0\gamma ^2}{1+\gamma }\right) ^{\frac{1}{2}} |{\varvec{D}}^{-\frac{1}{2}}{\varvec{\alpha }}|. \end{aligned}$$

(7.19)

Proof

Let us denote the derivation on $\hat{\Gamma }$ with a prime. Then

$$\begin{aligned} \hat{\pi }_j(\hat{\ell }) ^\prime = \sum _{n=1}^N \alpha _n \hat{\varphi }_n^\prime , \end{aligned}$$

and a straightforward computation gives

$$\begin{aligned} \begin{aligned} \Vert \hat{\pi }_j(\hat{\ell })^\prime \Vert ^2_{L^2(\hat{\Gamma })}&\le 2\left( \alpha _1^2 \left( \frac{1}{\hat{h}_0} \!+\! \frac{1}{\hat{h}_1}\right) \!+\! \alpha _2^2\left( \frac{1}{\hat{h}_0 + \hat{h}_1} + \frac{1}{\hat{h}_2}\right) + \sum _{n=3}^{N-2} \alpha _n^2\left( \frac{1}{\hat{h}_{n-1} }+ \frac{1}{\hat{h}_n}\right) \right. \\&\quad \left. + \alpha _{N-1}^2\left( \frac{1}{\hat{h}_{N-2}} +\frac{1}{ \hat{h}_{N-1} + \hat{h}_N}\right) + \alpha _{N}^2\left( \frac{1}{\hat{h}_{N-1}} + \frac{1}{\hat{h}_N}\right) \right) . \end{aligned} \end{aligned}$$

Hypothesis 7.1 yields

$$\begin{aligned}&\displaystyle \frac{1}{\hat{h}_0} + \frac{1}{\hat{h}_1} \le \frac{1}{2d_1}(1+ c_0\gamma ),\ \frac{1}{\hat{h}_0 + \hat{h}_1} + \frac{1}{\hat{h}_2} \le \frac{1}{3d_2}\left( c_0\gamma (1+\gamma ) + 2 + \frac{c_0\gamma ^2}{1+\gamma }\right) ,\\&\displaystyle \frac{1}{\hat{h}_{n-1} }+ \frac{1}{\hat{h}_n} \le \frac{2}{3d_n}(1+ c_0\gamma ),\\&\displaystyle \frac{1}{\hat{h}_{N-2}} +\frac{1}{ \hat{h}_{N-1} + \hat{h}_N} \le \frac{1}{3d_{N-1}}\left( c_0\gamma (1+\gamma ) + 2 + \frac{c_0\gamma ^2}{1+\gamma }\right) , \\&\displaystyle \frac{1}{\hat{h}_{N-1}} + \frac{1}{\hat{h}_N}\le \frac{1}{2d_N}(1+ c_0\gamma ). \end{aligned}$$

Then (7.19) follows readily from the fact that for $\gamma >1$,

$$\begin{aligned} c_0\gamma (1+\gamma ) + 2 + \frac{c_0\gamma ^2}{1+\gamma } > 2 (1+ c_0\gamma ). \end{aligned}$$

Comparing with (7.8) and the proof of Lemma 7.2, we see that a direct estimate of $\hat{\pi }_j(\hat{\varvec{\ell }})^\prime$ relies on a bound for $|{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|$, which we can hardly expect to be sharp. This difficulty can be bypassed by using the fact that $\hat{\varvec{\ell }}$ belongs to $H^1_0(\hat{\Gamma })^2$ and arguing as in [23]. Uniqueness of the solution of (4.24) in $\hat{X}_j$ implies that $\hat{\pi }_j(\hat{I}(\hat{\varvec{\ell }})) =\hat{I}(\hat{\varvec{\ell }})$ where $\hat{I}$ denotes the standard Lagrange interpolant in $\hat{X}_j$, that is well-defined because $\hat{\Gamma }$ is a line segment. This permits to write

$$\begin{aligned} \hat{\pi }_j(\hat{\varvec{\ell }})^\prime = \hat{\pi }_j(\hat{\varvec{\ell }}- \hat{I}(\hat{\varvec{\ell }}))^\prime + (\hat{I}(\hat{\varvec{\ell }})-\hat{\varvec{\ell }})^\prime + \hat{\varvec{\ell }}^\prime . \end{aligned}$$

(7.20)

First, we easily derive that

$$\begin{aligned} |\hat{I}(\hat{\varvec{\ell }})-\hat{\varvec{\ell }}|_{H^1(\hat{\Gamma })} \le 2|\hat{\varvec{\ell }}|_{H^1(\hat{\Gamma })}. \end{aligned}$$

Therefore

$$\begin{aligned} |\hat{\pi }_j(\hat{\varvec{\ell }})|_{H^1(\hat{\Gamma })} \le 3|\hat{\varvec{\ell }}|_{H^1(\hat{\Gamma })} + |\hat{\pi }_j(\hat{\varvec{\ell }}- \hat{I}(\hat{\varvec{\ell }}))|_{H^1(\hat{\Gamma })}, \end{aligned}$$

(7.21)

and it suffices to derive a bound for this last term. Let ${\varvec{M}}{\varvec{\alpha }}= {\varvec{b}}$ be the system (4.24) for a generic component of $\hat{\varvec{\ell }}- \hat{I}(\hat{\varvec{\ell }})$. Applying (7.12) and the analogue of (7.8), we obtain

$$\begin{aligned} |\hat{\pi }_j(\hat{\ell }-\hat{I}(\hat{\ell }))|_{H^1(\hat{\Gamma })} \le \Vert \big ({\varvec{I}}+ {\varvec{D}}^{-\frac{1}{2}}{\varvec{K}}{\varvec{D}}^{\frac{1}{2}}\big )^{-1}\Vert _2 |{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}| \le C |{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|, \end{aligned}$$

(7.22)

with the constant $C$ of (7.12), provided $c_0$ and $\gamma$ are chosen as in the proof of Proposition 7.1. Here we use the fact that (7.15) is also valid for $\Vert {\varvec{D}}^{-\frac{1}{2}}{\varvec{K}}^r{\varvec{D}}^{\frac{1}{2}}\Vert _2$. It remains to estimate $|{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|$.

Proposition 7.2

Let $\hat{\varvec{\ell }}$ belong to $H^1_0(\hat{\Gamma })^2$. If Hypothesis 7.1 holds with the constants $c_0$ and $\gamma$ chosen as in the proof of Proposition 7.1, then each component $\hat{\ell }$ of $\hat{\varvec{\ell }}$ satisfies

$$\begin{aligned} |{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}| < \sqrt{30} c| \hat{\ell }|_{H^1(\hat{\Gamma })}, \end{aligned}$$

(7.23)

where $c$ depends only on the interpolant $\hat{I}$. Therefore,

$$\begin{aligned} \forall \hat{\varvec{\ell }}\in H^1_0(\hat{\Gamma })^2,\quad |\hat{\pi }_j(\hat{\varvec{\ell }})|_{H^1(\hat{\Gamma })} < \big (3 +\sqrt{30} c C\big )| \hat{\varvec{\ell }}|_{H^1(\hat{\Gamma })}, \end{aligned}$$

(7.24)

with the constants $c$ and $C$ of (7.23) and (7.12).

Proof

We sketch the proof. To simplify, set $w = \hat{\ell }-\hat{I}(\hat{\ell })$. Arguing as in Lemma 7.2, we recover a bound for $|{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|$ by replacing $d_n$ by $d_n^3$ and $\hat{\ell }$ by $w$ in (7.10). The key point here is that the properties of the interpolant $\hat{I}$ imply

$$\begin{aligned} \Vert w\Vert _{L^2(\hat{x}_0,\hat{x}_1)}^2 \le c\big (\hat{h}_0^2|\hat{\ell }|^2_{H^1(\hat{x}_0,\hat{x}_1)} + \hat{h}_1^2|\hat{\ell }|^2_{H^1(\hat{x}_1,\hat{x}_2)}\big ), \end{aligned}$$

for a constant $c$ independent of $N$, with analogous expressions for the norms in the other subintervals. The factors involving $\hat{h}_n$ in $|{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|$ can be bounded by applying (7.11) with $c_0 \gamma =\frac{3}{2}$, as in the proof of Proposition 7.1. This gives

$$\begin{aligned} |{\varvec{D}}^{-\frac{3}{2}}{\varvec{b}}|^2&< 10 c \left( |\hat{\ell }|^2_{H^1(\hat{x}_0,\hat{x}_1)} + |\hat{\ell }|^2_{H^1(\hat{x}_0,\hat{x}_2)} + \sum \limits _{n=1}^N |\hat{\ell }|^2_{H^1(\hat{x}_{n-1},\hat{x}_{n+1})} + |\hat{\ell }|^2_{H^1(\hat{x}_N,\hat{x}_{N+1})} + |\hat{\ell }|^2_{H^1(\hat{x}_{N-1},\hat{x}_{N+1})}\right) , \end{aligned}$$

and (7.23) follows.

Finally, space interpolation between (7.13) and (7.24) gives

$$\begin{aligned} \forall \hat{\varvec{\ell }}\in H^{\frac{1}{2}}_{00}(\hat{\Gamma })^2,\quad |\hat{\pi }_j(\hat{\varvec{\ell }})|_{H^{\frac{1}{2}}_{00}(\hat{\Gamma })} < \hat{C}| \hat{\varvec{\ell }}|_{H^{\frac{1}{2}}_{00}(\hat{\Gamma })}, \end{aligned}$$

(7.25)

with a constant $\hat{C}$ independent of $N$.

1.1.2 Second example

In the first example, $\hat{\Lambda }$ and $\hat{\varvec{X}}_j$ have the same dimension, but of course this is not necessary. For the unique solvability of (3.8), it is sufficient that the set of degrees of freedom of $\hat{\Lambda }$ be an adequate subset of those of $\hat{\varvec{X}}_j$, sufficiently rich to guarantee a good approximation property of the Lagrange interpolant $\hat{I}$. Let us briefly give another simple choice of $\hat{\Lambda }$ with roughly half as many degrees of freedom as in the first example. Let $N$ be an odd integer, keep the same $\hat{\varphi }_0$ and $\hat{\varphi }_{N+1}$ as in (7.1), and choose

$$\begin{aligned} \begin{aligned} \hat{\varphi }_1(\hat{x})|_{[\hat{x}_{0},\hat{x}_{1}]}&= \frac{1}{\hat{h}_0 }(\hat{x}-\hat{x}_{0}),\quad \hat{\varphi }_1(\hat{x})|_{[\hat{x}_{1},\hat{x}_{2}]} = \frac{1}{\hat{h}_{1}}(\hat{x}_{2}-\hat{x}),\\ \hat{\varphi }_N(\hat{x})|_{[\hat{x}_{N-1},\hat{x}_{N}]}&= \frac{1}{\hat{h}_{N-1}},\quad (\hat{x}- \hat{x}_{N-1})\, \ \hat{\varphi }_N(\hat{x})|_{[\hat{x}_{N},\hat{x}_{N+1}]} = \frac{1}{\hat{h}_{N}}(\hat{x}_{N+1}- \hat{x}),\\ \hat{\varphi }_{2n}(\hat{x})|_{[\hat{x}_{2n-2},\hat{x}_{2n}]}&= \frac{1}{\hat{h}_{2n-2}+\hat{h}_{2n-1} }(\hat{x}-\hat{x}_{2n-2}),\\ \hat{\varphi }_{2n}(\hat{x})|_{[\hat{x}_{2n},\hat{x}_{2n+2}]}&= \frac{1}{\hat{h}_{2n}+ \hat{h}_{2n+1}}(\hat{x}_{2n+2}-\hat{x}),\quad 1 \le n\le \frac{N}{2}, \end{aligned} \end{aligned}$$

(7.26)

extended by zero elsewhere. We take

$$\begin{aligned} \hat{X}_j&= \left\{ \hat{\varvec{v}}\in H^1_0(0,1)^2;\,\hat{\varvec{v}}(\hat{x}) = \hat{\varvec{v}}_1\hat{\varphi }_{1}(\hat{x})+ \sum _{n=1}^{N/2} \hat{\varvec{v}}(\hat{x}_{2n})\hat{\varphi }_{2n}(\hat{x})+ \hat{\varvec{v}}_N\hat{\varphi }_{N}(\hat{x})\right\} ,\nonumber \\ \end{aligned}$$

(7.27)

$$\begin{aligned} \hat{\Lambda }&= \left\{ \hat{\varvec{\mu }}\in H^1(0,1)^2;\, \hat{\varvec{\mu }}(\hat{x})= \sum _{n=0}^{(N+1)/2} \hat{\varvec{\mu }}(\hat{x}_{2n})\hat{\varphi }_{2n}(\hat{x})\right\} . \end{aligned}$$

(7.28)

With this choice, (4.24) is uniquely solvable and it can be checked that all the results established for the first example carry over to this second example, with different constants.

1.2 The 3-D case

In addition to restricting the mesh in 3-D (see Remark 4.1), the above proofs are complex because they apply to a situation where the matrix of the system is irreducible. The proofs are much easier, when (3.8) represents local and independent conditions, but in general, this can only be achieved by suitably modifying the discrete velocity spaces. In this section we present an example for which (3.8) holds by explicitly constructing the solution of (4.3). The correction satisfies suitable continuity bounds that are needed to establish the stability estimate (3.25). We follow the approach of BenBelgacem [12] who presents a local construction in 3-D by adding to the space $X_{s,j}^h$ in ${\Omega }_{s,j}$ a stabilizing bubble function in each face $T^\prime$ of the trace ${\mathcal T}^h_{j,\Gamma _{ij}}$ of the triangulation ${\mathcal T}^h_j$ on $\Gamma _{ij}$ and choosing for $\Lambda ^H$ constant vectors on each face $T^\prime$. More precisely, for each $j$, $1 \le j \le M_s$, and for each $T$ in ${\mathcal T}^h_j$, let ${\mathcal P}(T)$ denote a polynomial space such as the mini-element or Bernardi–Raugel element, used in approximating the velocity of the Stokes problem with order one. For each face $T^\prime$ of ${\mathcal T}^h_{j,\Gamma _{ij}}$, let $T$ be the element of ${\mathcal T}^h_j$ with face $T^\prime$, and define

$$\begin{aligned} b_{T^\prime }|_{T} = \lambda _1\lambda _2 \lambda _3, \end{aligned}$$

where $\lambda _k$, $k=1,2,3$, denote the barycentric coordinates of the three vertices of $T^\prime$; it is extended by zero outside $T$. Then set

$$\begin{aligned} \begin{aligned} X_{s,j}^h = \{{\varvec{v}}\in {\mathcal C}^0(\overline{{\Omega }}_{s,j})^3;&\,\ \forall T \in {\mathcal T}^h_j, T\; \text{ not } \text{ adjacent } \text{ to }\; \Gamma _{ij}, {\varvec{v}}|_T \in {\mathcal P}(T),\\&\,\ \forall T \in {\mathcal T}^h_j, T\; \text{ adjacent } \text{ to }\; \Gamma _{ij}, {\varvec{v}}|_T \in {\mathcal P}(T)+ b_{T^\prime }{\mathbb {R}}^3\}, \end{aligned}\nonumber \\ \end{aligned}$$

(7.29)

and choose

$$\begin{aligned} \Lambda _H = \{ {\varvec{\mu }}_H \in L^2(\Gamma _{ij})^3;\, \forall T^\prime \in {\mathcal T}^h_{j,\Gamma _{ij}}, {\varvec{\mu }}_H|_{T^\prime } \in {\mathbb {P}}_0^3\}. \end{aligned}$$

(7.30)

As $b_{T^\prime }$ vanishes at all vertices of $T$, it does not change the approximating properties of ${\mathcal P}(T)$. Note that $\Lambda _H$ does not satisfy Hypothesis 3.2 (3). Nevertheless a discrete Korn inequality holds in $V_s^h$, see Propositions 7.3 and 7.4 below. With this choice, we can show that (3.8) holds. Indeed, for ${\varvec{v}}\in \tilde{X}$, it is easy to see that

$$\begin{aligned} {\varvec{v}}^h = \sum _{T^\prime \in {\mathcal T}^h_{j,\Gamma _{ij}}} {\varvec{v}}_{T^\prime }b_{T^\prime },\quad \text{ where } {\varvec{v}}_{T^\prime } = \frac{1}{\int _{T^\prime } b_{T^\prime }} \int _{T^\prime } {\varvec{v}}\end{aligned}$$

satisfies (3.8). We now define

$$\begin{aligned} {\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}}) = \sum _{T^\prime \in {\mathcal T}^h_{j,\Gamma _{ij}}} {\varvec{c}}_{T^\prime }b_{T^\prime },\quad \text{ where } {\varvec{c}}_{T^\prime } = \frac{1}{\int _{T^\prime } b_{T^\prime }} \int _{T^\prime } \big (\Theta ^h_s({\varvec{v}})|_{{\Omega }_{s,i}} - S^h({\varvec{v}})|_{{\Omega }_{s,j}}\big ),\nonumber \\ \end{aligned}$$

(7.31)

where $\Theta ^h_s({\varvec{v}})|_{{\Omega }_{s,i}}$ is computed in the preceding subsection by correcting $S^h({\varvec{v}})|_{{\Omega }_{s,i}}$ with ${\varvec{c}}_{i,\Gamma _{ij}}^h({\varvec{v}})$ defined in (4.17).

Lemma 7.4

The correction ${\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}})$ defined by (7.31) satisfies (4.3) and there exists a constant $C$ independent of $h$ and the diameter of ${\Omega }_{s,i}$, ${\Omega }_{s,j}$, and $\Gamma _{ij}$ such that for all ${\varvec{v}}$ in $H^1_0({\Omega })^n$

$$\begin{aligned} |{\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}})|_{H^1({\Omega }_{s,j})} \le C |{\varvec{v}}|_{H^1({\Omega }_{s,i}\cup {\Omega }_{s,j})}, \quad \Vert {\varvec{c}}_{j,\Gamma _{ij}}^h({\varvec{v}})\Vert _{L^2({\Omega }_{s,j})} \le C h |{\varvec{v}}|_{H^1({\Omega }_{s,i}\cup {\Omega }_{s,j})}.\nonumber \\ \end{aligned}$$

(7.32)

Proof

For any face $T^\prime$ of ${\mathcal T}^h_{j,\Gamma _{ij}}$, we can write

$$\begin{aligned} {\varvec{c}}_{T^\prime } = \frac{1}{\int _{T^\prime } b_{T^\prime }} \int _{T^\prime } \big (\Theta ^h_s({\varvec{v}})|_{{\Omega }_{s,i}}-{\varvec{v}}-(S^h({\varvec{v}})|_{{\Omega }_{s,j}}-{\varvec{v}})\big ). \end{aligned}$$

But on $\Gamma _{ij}$,

$$\begin{aligned} \Theta ^h_s({\varvec{v}})|_{{\Omega }_{s,i}} = S^h({\varvec{v}})|_{{\Omega }_{s,i}} + {\varvec{c}}_{i,\Gamma _{ij}}^h({\varvec{v}}), \end{aligned}$$

owing to the support of each correction. Therefore

$$\begin{aligned} {\varvec{c}}_{T^\prime } \!=\! \frac{1}{\int _{T^\prime } b_{T^\prime }} \int _{T^\prime } \big ({\varvec{c}}_{i,\Gamma _{ij}}^h({\varvec{v}}) + (S^h({\varvec{v}})|_{{\Omega }_{s,i}}-{\varvec{v}}) - (S^h({\varvec{v}})|_{{\Omega }_{s,j}}-{\varvec{v}})\big )= {\varvec{A}}_1 + {\varvec{A}}_2 + {\varvec{A}}_3. \end{aligned}$$

Let $T$ be the element of ${\mathcal T}^h_j$ adjacent to $T^\prime$. By arguing as in the proof of Lemma 4.1, we easily derive

$$\begin{aligned} |{\varvec{A}}_3 b_{T^\prime }|_{H^1(T)} \le \hat{C} |{\varvec{v}}|_{H^1(\Delta _T)}, \end{aligned}$$

(7.33)

where $\Delta _T$ is the macro-element of ${\mathcal T}^h_j$ required to define $S^h({\varvec{v}})$ in $T$. The estimation of ${\varvec{A}}_2$ is similar, but more technical because $T^\prime$ belongs to ${\mathcal T}^h_j$ whereas $S^h({\varvec{v}})|_{{\Omega }_{s,i}}$ is constructed on ${\mathcal T}^h_i$. Following the argument used in the proof of Lemma 4.3, we derive

$$\begin{aligned} |{\varvec{A}}_2 b_{T^\prime }|_{H^1(T)} \le \hat{C} \sum _{\ell }|{\varvec{v}}|_{H^1(\Delta _{T_\ell })}, \end{aligned}$$

(7.34)

where $\{T_\ell \}$ denote the set of elements of ${\mathcal T}^h_i$ that intersect $T$.

The bound for ${\varvec{A}}_1$ follows the same lines. With the notation of Lemma 4.1,

$$\begin{aligned} {\varvec{A}}_1 = \frac{1}{\int _{T^\prime } b_{T^\prime }} \int _{T^\prime } \sum _k {\varvec{c}}_k b_k, \end{aligned}$$

where the sum runs over the indices $k$ for which ${\mathcal O}_k \cap T^\prime \ne \emptyset$. According to Hypothesis 4.1, the number of terms in this sum is bounded by a fixed integer. Thus

$$\begin{aligned} |{\varvec{A}}_1| \le \sum _k \hat{C} \,\rho _k^{-\frac{1}{2}}|{\varvec{v}}|_{H^1(D_k)}, \end{aligned}$$

and Hypothesis 4.1 implies that

$$\begin{aligned} |{\varvec{A}}_1 b_{T^\prime }|_{H^1(T)} \le \hat{C} |{\varvec{v}}|_{H^1(\tilde{\Delta }_{T_\ell })}, \end{aligned}$$

(7.35)

where $\tilde{\Delta }_{T_\ell }$ is a macro-element in ${\Omega }_{s,i}$ and again the number of elements in $\tilde{\Delta }_{T_\ell }$ is bounded by a fixed integer. All constants are independent of $h$ and the diameter of ${\Omega }_{s,i}$, ${\Omega }_{s,j}$, and $\Gamma _{ij}$. Finally, the first inequality in (7.32) follows readily by summing (7.33)–(7.35) and applying Hypothesis 4.1. The argument for the second inequality in (7.32) is similar.

1.2.1 A discrete Korn inequality in $V_s^h$

Since all assumptions except Hypothesis 3.2 (3) hold, it suffices to examine the jump of functions of $V_s^h$ through the interfaces $\Gamma _{ij} \in \Gamma _{ss}$. The next two lemmas show that the projection of this jump on polynomials of ${\mathbb {P}}_1$ is small.

Lemma 7.4

Let $\Gamma _{ij} \in \Gamma _{ss}$, $i<j$. There exists a constant $C$, independent of $h$ and the diameters of $\Gamma _{ij}$, ${\Omega }_{s,i}$, and ${\Omega }_{s,j}$ such that

$$\begin{aligned} \forall {\varvec{v}}^h \in V_s^h, \forall {\varvec{p}}\in {\mathbb {P}}_1^3,\, \left| \,\,\int _{\Gamma _{ij}} [{\varvec{v}}^h]\cdot {\varvec{p}}\right| \le C h^{\frac{3}{2}} |\Gamma _{ij}|^{\frac{1}{2}} \big (|{\varvec{v}}^h|_{H^1(D_{s,i})} + |{\varvec{v}}^h|_{H^1(D_{s,j})}\big ),\nonumber \\ \end{aligned}$$

(7.36)

where $D_{s,k}$ denotes the layer of elements in ${\Omega }_{s,k}$ adjacent to $\Gamma _{ij}$.

Proof

All constants in this proof are independent of $h$ and the diameters of $\Gamma _{ij}$, ${\Omega }_{s,i}$, and ${\Omega }_{s,j}$. Let $T^\prime$ be an element (i.e. a face) of ${\mathcal T}^h_{j,\Gamma _{ij}}$, which is the mesh of $\Lambda ^H$. There is no loss of generality in assuming that $T^\prime$ lies on the $x_1-x_2$ plane. Consider a generic component $v^h$ of ${\varvec{v}}^h$. Since the jump already satisfies

$$\begin{aligned} \int _{T^\prime } [v^h] = 0, \end{aligned}$$

it suffices to bound the product of the jump by $x_k$, $k = 1,2$, say $x_1$. Then for any constant $c$,

$$\begin{aligned} \int _{T^\prime } [v^h] x_1 = \int _{T^\prime } \big ([v^h]-c\big ) \left( x_1 - \frac{1}{|T^\prime |}\int _{T^\prime } x_1\right) . \end{aligned}$$

A scaling argument gives

$$\begin{aligned} \left\| x_1 - \frac{1}{|T^\prime |}\int _{T^\prime } x_1 \right\| _{L^2(T^\prime )} \le \hat{C} |T^\prime |^{\frac{1}{2}} h_{T^\prime }. \end{aligned}$$

Similarly,

$$\begin{aligned} \inf _{c \in {\mathbb {R}}}\Vert [v^h]-c\Vert _{L^2(T^\prime )} \le \hat{C} h_{T^\prime } |[v^h]|_{H^1(T^\prime )} \le \hat{C} h_{T^\prime }\big (|v^h|_{{\Omega }_{s,i}}|_{H^1(T^\prime )} + |v^h|_{{\Omega }_{s,j}}|_{H^1(T^\prime )}\big ). \end{aligned}$$

On one hand, equivalence of norms gives

$$\begin{aligned} |v^h|_{{\Omega }_{s,j}}|_{H^1(T^\prime )} \le \hat{C} \,\rho _T^{-\frac{1}{2}}|v^h|_{{\Omega }_{s,j}}|_{H^1(T)}, \end{aligned}$$

where $T$ is the element of ${\mathcal T}^h_j$ adjacent to $T^\prime$. On the other hand, arguing as in the proof of Lemma 7.4, we prove that

$$\begin{aligned} |v^h|_{{\Omega }_{s,i}}|_{H^1(T^\prime )} \le \hat{C} \,\rho _T^{-\frac{1}{2}}|v^h|_{{\Omega }_{s,i}}|_{H^1(\Delta _T)}, \end{aligned}$$

where $\Delta _T$ is the union of all elements of ${\mathcal T}^h_i$ that intersect $T^\prime$. Then taking the product and summing over all faces $T^\prime$ of ${\mathcal T}^h_{j,\Gamma _{ij}}$, we obtain

$$\begin{aligned} \left| \,\,\int _{\Gamma _{ij}} [v^h] x_1 \right| \le \hat{C} h^{\frac{3}{2}} \left( \sum _{T^\prime \in {\mathcal T}^h_{j,\Gamma _{ij}}} |T^\prime |\right) ^{\frac{1}{2}} \big (|v^h|_{H^1(D_{s,i})} + |v^h|_{H^1(D_{s,j})}\big ), \end{aligned}$$

whence (7.36).

Lemma 7.6

Let $\Gamma _{ij} \in \Gamma _{ss}$, $i<j$, and let $\Pi ([{\varvec{v}}^h]) \in {\mathbb {P}}_1^3$ denote the projection of $[{\varvec{v}}^h]$ onto ${\mathbb {P}}_1^3$ on $\Gamma _{ij}$. There exists a constant $C$, independent of $h$ and the diameters of $\Gamma _{ij}$, ${\Omega }_{s,i}$, and ${\Omega }_{s,j}$ such that

$$\begin{aligned} \forall {\varvec{v}}^h \in V_s^h ,\quad \Vert \Pi ([{\varvec{v}}^h])\Vert _{L^2({\Gamma _{ij}})} \le C h^{\frac{3}{2}}\big (|{\varvec{v}}^h|_{H^1(D_{s,i})} + |{\varvec{v}}^h|_{H^1(D_{s,j})}\big ). \end{aligned}$$

(7.37)

Proof

By definition $\Pi ([{\varvec{v}}^h]) \in {\mathbb {P}}_1^3$ solves

$$\begin{aligned} \forall {\varvec{p}}\in {\mathbb {P}}_1^3,\quad \int _{\Gamma _{ij}} \Pi ([{\varvec{v}}^h])\cdot {\varvec{p}}= \int _{\Gamma _{ij}} [{\varvec{v}}^h]\cdot {\varvec{p}}. \end{aligned}$$

By passing to the reference subdomain $\hat{\Omega }_j$, this reads

$$\begin{aligned} \forall \hat{\varvec{p}}\in {\mathbb {P}}_1^3,\quad \int _{\hat{\Gamma }} \Pi ([{\varvec{v}}^h])\circ F_j\cdot \hat{\varvec{p}}= |\hat{\Gamma }|\,|\Gamma _{ij}|^{-1} \int _{\Gamma _{ij}} [{\varvec{v}}^h]\cdot {\varvec{p}}. \end{aligned}$$

The coefficients of the polynomial of degree one $\Pi ([{\varvec{v}}^h])\circ F_j$ solve a linear system whose matrix only depends on $\hat{\Gamma }$. Therefore, in view of (7.36),

$$\begin{aligned} \Vert \Pi ([{\varvec{v}}^h])\Vert _{L^2(\Gamma _{ij})} \le |\Gamma _{ij}|^{\frac{1}{2}}\Vert \Pi ([{\varvec{v}}^h])\circ F_j\Vert _{L^\infty (\hat{\Gamma })} \le \hat{C} h^{\frac{3}{2}} \big (|{\varvec{v}}^h|_{H^1(D_{s,i})} + |{\varvec{v}}^h|_{H^1(D_{s,j})}\big ). \end{aligned}$$

This last result enables us to prove Korn’s inequality in $V_s^h$.

Proposition 7.3

Let $|\Gamma _s| >0$ and ${\Omega }_s$ be connected. Then there exists $h_0 >0$ such that for all $h \le h_0$,

$$\begin{aligned} \forall {\varvec{v}}^h\in V_s^h,\quad \sum _{i=1}^{M_s} |{\varvec{v}}^h|^2_{H^1({\Omega }_{s,i})} \le C \sum _{i=1}^{M_s} \Vert {\varvec{D}}({\varvec{v}}^h)\Vert ^2_{L^2({\Omega }_{s,i})}; \end{aligned}$$

(7.38)

the constants $C$ and $h_0$ are independent of $h$ and the diameters of the interfaces $\Gamma _{ij}$ and the subdomains ${\Omega }_{s,k}$.

Proof

Let ${\varvec{v}}^h \in V_s^h$. Formula (1.12) in [16] gives, with a constant $C_1$ that depends only on the shape regularity of the mesh of subdomains ${\mathcal T}_{\Omega }$,

$$\begin{aligned} \begin{aligned}&\sum _{i=1}^{M_s} |{\varvec{v}}^h|^2_{H^1({\Omega }_{s,i})} \\&\quad \le C_1 \left( \sum _{i=1}^{M_s} \Vert {\varvec{D}}({\varvec{v}}^h)\Vert ^2_{L^2({\Omega }_{s,i})} + \sum _{i<j} \frac{1}{\mathrm{diam}(\Gamma _{ij})}\Vert \Pi ([{\varvec{v}}^h]) \Vert ^2_{L^2(\Gamma _{ij})} \right) \\&\quad \le C_1\left( \sum _{i=1}^{M_s} \Vert {\varvec{D}}({\varvec{v}}^h)\Vert ^2_{L^2({\Omega }_{s,i})} + \hat{C}\sum _{i<j}\frac{1}{\mathrm{diam}(\Gamma _{ij})} h^3 \big (|{\varvec{v}}^h|^2_{H^1({\Omega }_{s,i})} + |{\varvec{v}}^h|_{H^1({\Omega }_{s,j})}^2\big )\right) , \end{aligned} \end{aligned}$$

owing to (7.37). But $h < \mathrm{diam}(\Gamma _{ij})$ and there exists an $h_0 >0$ such that

$$\begin{aligned} \forall h \le h_0,\quad h^2\,(C_1 \hat{C})^{-1} \le \frac{1}{2}. \end{aligned}$$

Since $C_1$ and $\hat{C}$ are independent of $h$ and the diameters of the interfaces $\Gamma _{ij}$ and the subdomains, then so is $h_0$. Hence for all $h \le h_0$,

$$\begin{aligned} \sum _{i=1}^{M_s} |{\varvec{v}}^h|^2_{H^1({\Omega }_{s,i})} \le 2 C \sum _{i=1}^{M_s} \Vert {\varvec{D}}({\varvec{v}}^h)\Vert ^2_{L^2({\Omega }_{s,i})}. \end{aligned}$$

By arguing as in the proof of Lemma 3.4, we easily derive Korn’s inequality when $|\Gamma _s| =0$ and ${\Omega }_s$ is connected.

Proposition 7.4

Let $|\Gamma _s| =0$ and ${\Omega }_s$ be connected, i.e. $\Gamma _{sd} = \partial {\Omega }_s$. Then there exists $h_0 >0$ such that for all $h \le h_0$,

$$\begin{aligned}&\forall {\varvec{v}}^h\in V_s^h,\nonumber \\&\quad \sum _{i=1}^{M_s} |{\varvec{v}}^h|^2_{H^1({\Omega }_{s,i})} \le C \sum _{i=1}^{M_s} \left( \Vert {\varvec{D}}({\varvec{v}}^h)\Vert ^2_{L^2({\Omega }_{s,i})} + \left( \sum _{l=1}^2 \int _{\Gamma _{sd}} |{\varvec{v}}^h_s \cdot {\varvec{\tau }}_l|\right) ^2\right) ;\qquad \qquad \end{aligned}$$

(7.39)

the constants $C$ and $h_0$ are independent of $h$ and the diameters of the interfaces $\Gamma _{ij}$ and the subdomains ${\Omega }_{s,k}$.

The case when ${\Omega }_s$ is not connected follows from these two propositions applied to each connected component of ${\Omega }_s$ according that it is or not adjacent to $\Gamma _s$.